基于置信度变换的交直流混联输电系统区间潮流方法与流程

本发明涉及一种基于置信度变换的交直流混联输电系统区间潮流(iopf)方法，属电力输送
技术领域：
。
背景技术：
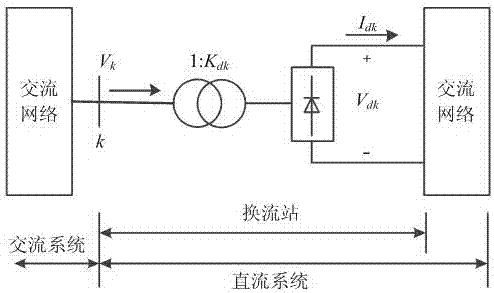
：高压直流输电不仅在功率控制方面具有快速性和灵活性，而且在远距离跨区域、大容量输送电能上优势明显，已成为现代电网互联的重要方式。2020年国家电网将建成“三华”特高压同步电网骨干网架，建成“四纵七横”特高压目标网架和21回特高压直流，特高压交直流混联系统在高压输电中扮演着越来越重要的角色，直流系统逐渐成为影响电力系统规划与运行的关键因素之一。另外，由于设备故障或检修，系统参数的测量、传输等误差以及近年来新能源发电的规模性并网使得电力系统的分析与计算需要面对更多不确定性因素。为了帮助相关人员更全面地获取系统的运行信息，捕捉系统的薄弱环节及潜在危机，对交直流混联系统进行不确定性分析计算显得尤为必要。近年来，一些学者对交直流混联系统的不确定性分析进行了诸多有益探索。比如，采用实用化概率的方法进行稳定性分析，完善了系统和节点的风险指标。但概率数学的方法必须以大量的历史数据为基础，以构造精确的概率分布函数；一种适于求解含新能源的交直流混联系统的区间最优潮流问题，并将区间问题转化为两个确定性问题求解，取得了较好的计算效果。其采用的区间数学只需区间变量的外延参数，建模方便，对历史数据的依赖度较少。pdt(probabilitydegreetransformation)是一种将区间优化模型转换为确定性数学模型求解的转换方法，叫作置信度变换。技术实现要素：本发明的目的是，为了解决交直流混联系统的不确定性问题，提出一种基于置信度变换的交直流混联输电系统区间潮流方法一种基于置信度变换的交直流混联输电系统区间潮流方法，其特征在于，所述方法包括如下步骤：(1)以交直流区间参数形式刻画系统中的不确定变量，建立交直流混联系统的区间潮流模型；(2)对置信度变换(pdt)的方法进行适应性推导，将区间优化模型转换为确定性数学模型，实现含区间不确定变量的约束转换；(3)采用预测校正原始对偶内点方法分别对转换后的确定性模型进行求解，通过修正方程计算仿射方向，得到仿射扰动因子后回代得到校正方向，进而得到修正量。本发明步骤(1)中所述交直流混联系统的区间潮流模型如下：目标函数如下式：式中，目标函数f(x)为系统损耗；sg为发电机节点集合；pgi为节点i发电机有功功率pdi为节点i负荷的有功功率。交流系统潮流方程等式约束如下式：式中，vi为节点i的电压幅值；δi为节点i的电压相角；iac为与交流节点i所联接支路的对应节点集合；qri为节点i无功电源无功功率；yij为节点导纳矩阵第i行j列元素的幅值，αij为对应的相角，δij＝δi-δj-αij；i,j∈sb，sb为节点集合。直流系统潮流方程等式约束如下式：式中，k∈sd，sd为直流节点集合；idc为与直流系统节点i所联接支路对应的节点集合；idk和idk分别表示直流节点k的电流和电压；为直流节点k的换流器功率因数角；正、负号分别对应于整流器和逆变器。换流器方程及直流网络方程等式约束如下式：式中，θdk为直流节点k的换流器控制角；xck为直流节点k的换流器换相电抗；kγ表示由换流器换相电抗产生的换相系数；gdkj为消去联络节点后的直流网络节点电导矩阵gd的元素；sdk为换流站类型，“+1”表示整流测，“-1”表示逆变侧。系统安全约束和直流变量约束如下式：式中，spv为pv(发电机)节点集合；spq为pq节点集合；和(·)分别代表变量(·)的上、下限。本发明步骤(1)中所述交直流系统区间参数表示如下：与常规opf模型不同，式(1)-(5)的交直流混联系统opf模型考虑变量的不确定性，并以区间数的形式表示，考虑负荷功率以服从区间分布的随机变量表示如下：式中，和分别为有功负荷变量区间分布的上下界；和分别为无功负荷变量区间分布的上下界。将式(6)代入式(1)-(5)的交直流混联系统opf模型，即转换成交直流混联系统的iopf模型，一个包含区间不确定变量的非线性区间优化问题。本发明步骤(2)中所述含区间不确定变量的约束转换如下：区间优化方法只需区间变量的外延参数，无需构造精确的概率分布模型，本发明假设区间变量[x]±＝[x-,x+]服从均匀分布，x<[x±]的置信度定义为：引入置信度λ，λ∈[0,1]，则p(x<[x±])≥λ可转换为：x≤x-λ+x+(1-λ)(8)同理，p(x>[x±])≥λ可转换为：x≥x+λ+x-(1-λ)(9)当λ＝0时，式(8)表达为x<x+，表示决策者只关心区间上边界，即完全乐观；当λ＝1时，式(8)等效为x<x-，表示决策者更倾向于下边界取值，即完全悲观，即λ的取值体现了决策者对不确定变量的谨慎程度。由式(7)-式(9)可以看出：置信度λ是将区间变量的边界信息转换为确定性变量的比例参数，是根据具体应用场景而设定的，以实现不同电网运行场景的切换。区间不确定变量转换方法思路为：利用区间置信度公式，使区间约束条件成立的概率满足给定的区间置信度水平，从而实现区间约束条件的确定性转化。对于一般含区间变量的非线性优化问题：式中：[x-,x+]为不等式约束区间；[y-,y+]为等式约束区间。引入区间不等式约束变量的置信度λx＝[λx1,λx2,...,λxm]t，m为含区间变量不等式约束数。根据式(7)-式(9)的转换方式，式(10)中的区间不等式约束可转换为：同理，由于区间等式约束可转化为两个不等式约束，引入的置信度λy＝[λy1,λy2,...,λyl]t，式(10)中的区间等式约束采用如下转换方式：式中，n为含区间变量等式约束数。本发明步骤(3)中所述预测校正原始对偶内点法基于原对偶内点法理论，通过修正方程计算仿射方向，得到仿射扰动因子后回代得到校正方向，进而得到修正量。1、原对偶内点法opf计算模型可简化为非线性优化形式：式中，f(x)为目标函数；h(x)为等式约束函数；g(x)为不等式约束函数，g和分别为其下、上限。原对偶内点法求解该非线性规划问题的步骤如下：首先，引入松弛变量，并将模型转换为拉格朗日函数形式：式中，y，z，w均为拉格朗日乘子；μ为引入的障碍常数；l，u为不等式约束的松弛变量；r为不等式个数。由一阶最优性条件，导出kkt方程组：其中，l,u,z,w为r×r全对角矩阵，由上式的最后两个方程可以解得μ＝(ltz-utw)/(2r)，定义对偶间隙gap＝ltz-utw。为提高算法收敛效率，引入中心参数σ，障碍常数μ＝σgap/(2r)。牛顿–拉夫逊法处理式(15)的非线性方程组，将其线性化，可转换为如下自治常微分方程组：式中，和分别为h(x)和g(x)海森矩阵的线性叠加。2、预测校正原始对偶内点法通过预测步求出仿射方向修正量，然后利用其估计互补方程泰勒展开式的2阶项，求出校正步修正量。算法在每次迭代中只增加1次回代运算，可有效减少迭代次数，提高收敛速度。预测校正步骤如下：一、预测步1)设定中心参数σ＝0；2)求解式(16)，得到仿射方向δxaff、δyaff、δzaff、δlaff、δuaff、δwaff；3)确定迭代步长和4)计算仿射方向的互补间隙gapaff；5)根据当前点的对偶间隙与仿射方向下的对偶间隙间的关系动态确定中心参数值：δ＝(gapaff/gap)3(19)式中，对偶间隙gap＝ltz-utw。二、校正步6)对互补松弛条件进行校正7)l'x校正为：本发明的有益效果是：本发明中采用的pdt方法对不确定性问题转换效率较高，可灵活方便地将区间不确定变量进行确定性转换；区间优化的结果可为决策者对交直流混联输电系统进行合理的风险控制和规划提供重要参考，两者结合应用对于推动交直流混联系统的发展具有重要意义。附图说明图1为交直流系统的示意图；图2为不同λ条件下的计算结果；图3为节点电压幅值计算结果；图4为各发电机优化结果。具体实施方式下面结合本发明实施例，对本发明进行详细的描述。本实施例一种基于置信度变换的交直流混联输电系统区间潮流方法，包括如下步骤：1)初始化。读入交直流系统参数，给定原始与对偶变量初值，初始化迭代次数iter等；2)确定
发明内容中式(6)负荷功率的区间分布情况，并将其代入
发明内容中式(1)-(5)的交直流混联最优潮流模型；3)采用
发明内容中式(11)-(12)对iopf模型进行置信度变换，设定置信度值，将原区间问题进行确定性转换；4)应用预测校正原始对偶内点法求解转换后的确定性模型；5)判断对偶间隙gap≤ε是否成立，若不满足，转到步骤6)，若满足，输出计算结果；6)迭代次数iter＝iter+1，若iter小于最大迭代次数，转步骤4)，否则终止计算，调试程序。以下为以ieee30系统为基础，基于置信度变换的iopf问题的具体事例。将6-7交流支路使用直流线路替代，形成交直流混联输电系统。换流站变压器电压比调节范围为10％，节点6为整流侧，节点7为逆变侧；整流侧与逆变侧换相电阻xc1＝xc2＝0.015；换流器功率因数取0.96。表1和图2给出了ieee-30节点系统负荷5种不同置信度情况下的计算结果。可以看出：负荷功率预测区间的置信度越大，负荷水平越低，则发电机总有功出力越高，系统的网损也随着置信度λ的增加而减小。表1不同λ条件下的计算结果置信度00.250.500.751.00目标函数/mw2.522.362.182.081.95总有功出力/mw314.26299.93285.57271.31257.01由于置信度λ是考虑了调度运行决策者对系统的不确定因素的乐观程度，即区间负荷功率的预测值。表3的结果表明，置信度转换的方法能够将不确定因素融入到本文的区间优化模型中，该方法对于交直流混联输电系统进行合理的风险控制以及规划具有重要的指导意义。由
发明内容中式(12)可知，λ＝1时，hl(x)＝yl-对应于本文的负荷区间下限值，即对负荷功率预测较为悲观；同理，当λ＝0时，对应于负荷区间上限值，即对负荷功率预测较为乐观。λ＝1或λ＝0是较为极端情况，接下来将基于一般情况(λ取0.25)分析。表2系统idopf计算结果图3和表2分别为λ＝0.25时ieee-30节点交直流混联系统各节点电压幅值和iopf的计算结果。可以看出，iopf得到了负荷区间不确定性影响下优化目标的区间，其给出的是系统资源协调利用的两个极端情况；结合置信度转换的方法，可根据实际负荷情况对置信度设置值进行调整，实现不同负荷条件下系统的运行情况的计算。图4为ieee-30节点系统各个发电机出力优化结果。可以看出，通过置信度转换后的发电机出力结果均处于区间优化法求得的区间边界内，置信度转换的求解结果考虑了决策者对系统的风险信息和实际的调控要求信息等，给出了在区间计算范围及明确的调度结果。同时，区间优化法的电压幅值区间上、下边界结果可为运行人员进行安全评估提供重要支撑。上面对本发明的较佳实施方式作了详细说明，但是本发明并不限于上述实施方式，在本领域的普通技术人员所具备的知识范围内，还可以在不脱离本发明宗旨的前提下做出各种变化。当前第1页12