一种智能电力负载识别方法与流程
本发明涉及电力负载识别领域,特别涉及一种基于深度学习的智能电力负载识别方法。
背景技术:
资源环境的制约是伴随我国经济社会发展所面临的突出矛盾,如何促进节能减排,是解决节能环保问题的核心关键,具有十分重要的意义。而节能减排合理优化能源结构的前提在于对电路中的负载设备进行识别,传统电路中负载的识别方法需要在各个负载前加装传感器,所需成本高,并需对原有电路进行修改。
技术实现要素:
有鉴于此,本发明提供了一种智能电力负载识别方法,不需要在各个负载前加装传感器,利用深度学习方法即可对总进线的电流与电压的变化进行记录与识别,从而实现无损的低成本负载识别。
为了解决上述技术问题,本发明是这样实现的。
一种智能电力负载识别方法,包括:
步骤1、模拟日常用电情况,在电路中增减电器以实现电路总负载的变化,记录负载变化时的电路总进线的电参量变化量x(i),同时将x(i)对应的当前电路负载情况记为图节点数据g(i);
其中,在电参量发生变化的第i时刻,将电参量的变化数据加上当时的时间和环境附加数据,记为第i时刻的电参量变化量x(i);图节点数据g(i)由n个子节点
步骤2、因为子节点数目不固定,导致图节点数据g(i)维度不固定,对图节点数据g(i)进行快速傅里叶变换,将其转为固定维度的图节点频域数据h(i);所述电参量变化量x(i)和图节点频域数据h(i)构成训练样本;
步骤3、利用隐性马尔科夫模型对电参量变化量x(h)和图节点频域数据h(h)进行建模,将图节点频域数据视为电参量变化量的隐变量,而图节点频域数据h(i)只受到上一时刻的图节点频域数据h(i-1)的影响;
步骤4、使用自循环神经网络来实现隐马尔科夫模型;自循环神经网络的输入为i时刻的电参量变化量x(i)和i-1时刻的图节点频域数据h(i-1),输出为i时刻的图节点频域数据h(i);采用步骤2获取的训练样本对自循环神经网络进行循环训练;
步骤5、实际负载识别时,根据电路中的初始负载状态构建初始图节点数据g(0)并转化为初始图节点频域数据h(0);当电路中出现负载变化时,令i=1,获取电路中的电参量变化量x(1),将x(1)和h(0)输入到自循环神经网络中,输出h(1),对h(1)进行逆傅里叶变换即可得到图节点数据g(1);每当电路中负载变化时,i自加1,均进行一次自循环神经网络的循环计算,自循环神经网络利用x(i)和h(i-1)计算出输出h(i),对h(i)进行逆傅里叶变换获得图节点数据g(i),根据g(i)识别出电路中的当前负载状态。
优选地,所述步骤2中,对图节点数据g(i)进行傅里叶变换,将其转为固定维度的图节点频域数据h(i)为:
设g(i)中当前包含了n个子节点,每个子节点由2个数据组成,则g(i)可表示为一个n×2维的数组,利用快速傅里叶变换算法将g(i)的n×2维的数组转为m×2维的频域数据,其中m为预先设定的频域采样个数,取值上确保m总是大于实际使用中g(i)子节点的个数n。
优选地,所述步骤4中,对h(i)进行逆傅里叶变换获得图节点数据g(i)为:
对自循环神经网络输出的m×2维的h(i)进行逆傅里叶变换后,得到m×2维的数据记为原始数据
优选地,家用场景中m设置为100,工业用电环境中m设置为1000。
优选地,在步骤1在电路总负载的单次变化时,仅变更一个电器负载。
优选地,电路中出现负载变化的识别方式为:在电路的总进线处安装智能电表,实现电路中电参量的采集,根据电参量的突变识别负载变化。
优选地,所述电参量变化量x(i)中的所述电参量的变化数据包括电路中总的有功功率、无功功率、视在功率、电压电流真有效值、相角和频率的变化量。
优选地,对于x(1),其中的电参量的变化数据采用第一次记录的电参量数据,而不用变化量。
优选地,所述电参量变化量x(i)中的环境附加数据包括当前的时间、气温和空气湿度。
有益效果:
(1)本发明从电路总进线获取电参量变化量,并获取当前电路负载情况,将这些数据组成训练样本对自循环神经网络进行训练,令自循环神经网络能够反映电参量变化量与电路负载情况的映射关系。通过这样的深度学习方法,不需要在各个负载前加装传感器,只需要获取电路总的电参量数据即可实现负载的智能识别。
(2)本发明利用了时间、温度以及湿度等环境状态数据,辅助电路中负载的识别,有效的提升了识别的精度;
(3)本发明使用图与子节点的编码方式对电路中电参量变化引起的负载变化进行记录,能够快速的建立训练数据集。
(4)本发明利用傅里叶变换方法,将图中非结构化的子节点映射至频域空间,实现数据的结构化,方便后续自循环数据网络的训练与使用。
附图说明
图1为本发明图节点的组成示意图。
图2为本发明隐形马尔科夫模型的示意图。
具体实施方式
下面结合附图并举实施例,对本发明进行详细描述。
本发明提供了一种智能电力负载识别方法,该方法从电路总进线获取电参量变化量,并获取当前电路负载情况,将这些数据组成训练样本对自循环神经网络进行训练,令自循环神经网络能够反映电参量变化量与电路负载情况的映射关系。
本发明提供的智能电力负载识别方法,包括如下步骤:
步骤1、在电路的总进线处安装智能电表,实现电路中总的电参量数据的测量和采集。
本发明选取的电参量包括有功功率、无功功率、视在功率、电压电流真有效值、相角、频率等电参量。
步骤2、当电路中的电参量发生变化时,将第i次电参量的变化量数据加上此时的时间和环境附加数据,组成表征当前负载变化情况的特征参量,记为电参量变化量x(i),
其中,本发明在电参量数据上增加时间和环境数据,是考虑到用电习惯的问题。可能在特定时间开启洗衣机,或者在特定时间使用微波炉,可能气温高时使用空调几率大。因此,增加环境和时间数据能够令神经网络的学习更为准确。优选地,环境附加数据选取当前时间(精确到秒)、气温、空气湿度。
步骤3、将电参量变化量x(i)所对应的当前电路负载情况记为图节点g(i)。
如图1所示,图节点中包含n个子节点
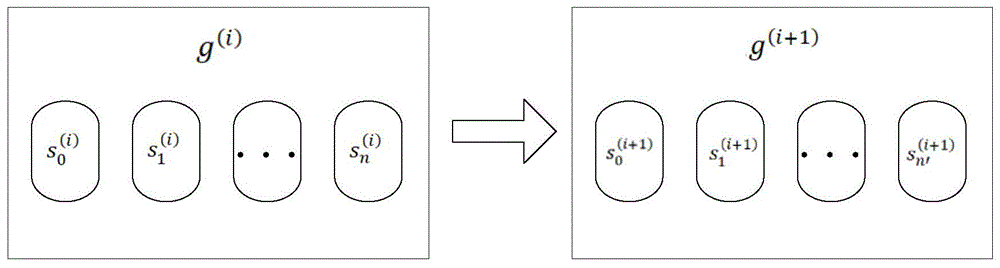
图节点数据g(i)是通过对前一时刻的图节点数据g(i-1)添加、删除子节点而得到。图节点g(i)只与上一时刻的图节点g(i-1)有关。例如,增加电热水器的使用,关闭洗衣机,或者电冰箱功率发生变化,都会导致图节点发生变化。
步骤4、模拟日常用电情况,在电路中增减电器以实现电路总负载的变化,记录负载变化时的电路总进线的电参量变化量x(i),同时将x(i)对应的当前电路负载情况记为图节点数据g(i)。为了便于后续的神经网络训练,在电路总负载的单次变化时,仅变更一个电器负载。
其中,x(i)对应的图节点数据g(i)由g(i-1)中增减子节点得到,并记录下对应增减子节点的负载类型
步骤5、因为子节点数目不固定,导致图节点数据g(i)的维度不固定,因此对图节点数据g(i)进行傅里叶变换,将其转为固定维度的图节点频域数据h(i);以便后续算法模型计算。所述电参量变化量x(i)和图节点频域数据h(i)构成训练样本。
由于原始数据集中图节点g(i)中所包含的子节点的数目不固定,因此,使用傅里叶变换将子节点的数据转为固定长度的频域数据h(i)后再送入神经网络模型进行训练。
具体做法为:假设g(i)中包含了n个子节点,每个子节点包含负载类型与负载功率两个数据,即g(i)可表示为一个
步骤6、利用隐性马尔科夫模型对电参量变化量x(i)和图节点频域数据h(i)进行建模,将图节点频域数据视为电参量变化量的隐变量,而图节点频域数据h(i)只受到上一时刻的图节点频域数据h(i-1)的影响。如图2所示。
步骤7、使用自循环神经网络来实现隐马尔科夫模型,并对自循环神经网络进行训练。
自循环神经网络的输入为i时刻的电参量变化量x(i)和i-1时刻的图节点频域数据h(i-1),输出为i时刻的图节点频域数据h(i);采用步骤3获取的训练样本对自循环神经网络进行循环训练。在训练时,因为x(i)和h(i)是i逐渐增加的连续数据,首先输入x(1)和h(0),神经网络输出h(1),将输入值与训练样本中的真实值进行比对并计算出损失函数,从而实现一次循环;然后将x(2)和上一轮的输出值h(1)再输入自循环神经网络后输出h(2),依次类推,当完成训练数据中的某一序列中的所有样本后,利用反向传播算法对自循环神经网络的参数进行更新,最终完成自循环神经网络的训练。
步骤8、实际负载识别时,根据电路中的初始负载状态构建初始图节点数据g(0)并转化为初始图节点频域数据h(0);当电路中出现负载变化时,令i=1,获取电路中的电参量变化量x(1),将x(1)和h(0)输入到自循环神经网络中,输出h(1),对h(1)进行逆傅里叶变换即可得到图节点数据g(1);每当电路中负载变化时,i自加1,均进行一次自循环神经网络的循环计算,自循环神经网络利用x(i)和h(i-1)计算出输出h(i),对h(i)进行逆傅里叶变换获得图节点数据g(i),根据g(i)识别出电路中的当前负载状态。
其中,对h(i)进行逆傅里叶变换获得图节点数据g(i)的计算过程为:对于本方案加入如下约束,从图g(i)到图g(i+1)的负载变化过程中,子节点的增减个数最多为1个,即g(i)与g(i+1)中n的数目变化不能超过1。为实现这一点,先将神经网络输出的
至此,本流程结束。
以上的具体实施例仅描述了本发明的设计原理,该描述中的部件形状,名称可以不同,不受限制。所以,本发明领域的技术人员可以对前述实施例记载的技术方案进行修改或等同替换;而这些修改和替换未脱离本发明创造宗旨和技术方案,均应属于本发明的保护范围。
- 还没有人留言评论。精彩留言会获得点赞!