一种基于反行波曲率的柔性直流输电线路保护方法

1.本发明属于电力系统领域，涉及直流输电线路的继电保护技术领域，具体涉及一种基于反行波曲率的柔性直流输电线路保护方法。


背景技术：

2.随着化石能源的日渐枯竭和环境问题的日益严重，世界各国均提出了从化石能源向可再生能源转变的发展规划。传统高压直流输电在电力系统中肩负着能源产地与负荷中心间输送电能的重任，在远距离、大容量电能传输及非同步电网互联等应用场合具有明显优势。随着电力电子器件和控制技术的发展，柔性直流输电技术已经实现，突破了换相失败、无功补偿等传统直流输电技术的固有瓶颈，适用于清洁能源并网、海上平台供电、城市异步电网互联、孤岛供电等技术等场景。
3.然而，柔性直流输电系统是一个“低惯量”系统，故障后电流上升速度快且幅值大，若不及时切除故障将很快影响到整个系统，因此快速可靠的线路保护是保障其安全稳定运行的关键。
4.对于柔性直流电网，故障隔离与清除方案采用“半桥型mmc+直流断路器”，为减小故障的影响范围，直流电网应具备快速识别、定位故障的能力，进而实现故障隔离。然而，高阻故障和雷击干扰场景下，保护原理的识别、定位故障的能力将被弱化，严重影响其可靠性，亟待提出具有强耐受过渡电阻和雷击干扰能力的保护原理。现有研究成果可概括为四类，分别基于线路故障电气量的频域特征，线路故障电气量的时域特征，人工智能算法，线路边界(波阻抗不连续点)特性。然而，现有原理普遍存在耐过渡电阻能力弱，保护阈值的整定依赖仿真数据，对采样频率和计算能力要求高等问题。


技术实现要素：

5.为解决上述现有技术存在的问题，本发明的目的是提供一种基于反行波曲率的柔性直流输电线路保护方法，本发明方法耐受过渡电阻能力强，保护阈值的整定不依赖于仿真数据，对采样频率和计算能力要求低。
6.为达到上述目的，本发明采用的技术方案是：
7.一种基于反行波曲率的柔性直流输电线路保护方法，包括如下步骤：
8.步骤一：采样柔性直流输电线路正极、负极的电压和电流，计算1模、0模的电压和电流，计算1模电压反行波；
9.根据式(1)计算1模电压u
(1)
、0模电压u
(0)
、1模电流i
(1)
、0模电流i
(0)
，
[0010][0011]
式中，q为变换矩阵，u
p
为正极电压，un为负极电压，i
p
为正极电流，in为负极电流；
[0012]
根据式(2)的1模电压u
(1)
和1模电流i
(1)
的定义式推导电压反行波u
b(1)
的表达式，如式(3)所示，
[0013][0014]
式中，u
f(1)
为1模电压前行波，u
b(1)
为1模电压反行波，i
f(1)
为1模电流前行波，i
b(1)
为1模电流反行波，zc为波阻抗。
[0015]ub(1)
＝[u
(1)-i
(1)
·
zc]/2
ꢀꢀꢀ
(3)
[0016]
根据式(3)，由1模电压u
(1)
、1模电流i
(1)
计算1模电压反行波u
b(1)
；
[0017]
步骤二：计算1模电压梯度，进行启动元件判别，若判据满足，则为故障，继续执行，否则返回步骤一；
[0018]
启动元件的判别式如式(4)所示，
[0019][0020]
式中，k和j是采样序号，u
(1)
(k-j)为第k-j个采样时刻对应的1模电压，为第k个计算得到的1模电压梯度，ε1是启动元件的阈值，其整定原则如式(5)所示，
[0021][0022]
式中，rel1是启动元件阈值整定的可靠系数，是稳态阶段电压波动产生的最大梯度；
[0023]
步骤三：计算1模电流梯度，进行方向元件判别，若判据满足，则为正向故障，继续执行，否则返回步骤一；
[0024]
方向元件的判别式如式(6)所示，
[0025][0026]
式中，i
(1)
(k-j)为第k-j个采样时刻对应的1模电流，为第k个计算得到的1模电流梯度，ε2是方向元件的阈值，其整定原则如式(7)所示，
[0027][0028]
式中，rel2是方向元件阈值整定的可靠系数，是稳态阶段电流波动产生的最大梯度；
[0029]
步骤四：计算1模电压反行波曲率的对数值，进行选区元件判别，若判据满足，则为区内故障，继续执行，否则返回步骤一；
[0030]
1模电压反行波曲率κ
b(1)
的计算公式如式(8)所示，
[0031][0032]
式中，u
″
b(1)
为1模电压反行波的二次导数，u
′
b(1)
为1模电压反行波的一次导数，由1
模电压反行波u
b(1)
根据式(9)计算得到；
[0033][0034]
式中，u
b(1)
(k)为第k个采样时刻对应的1模电压反行波，u
′
b(1)
(k)为第k个计算得到的1模电压反行波的一次导数，u
″
b(1)
(k)为第k个计算得到的1模电压反行波的二次导数，ts为采样间隔；
[0035]
选区元件的判别式如式(10)所示，
[0036]
max{lgκ
b(1)
(k-i)}＞ε3,i＝0,1,
…
,4
ꢀꢀꢀ
(10)
[0037]
式中，lgκ
b(1)
是1模电压反行波曲率的对数值，ε3是选区元件的阈值，其整定原则如式(11)，
[0038]
ε3＝rel3·
lgκ
b(1)(max)
ꢀꢀꢀ
(11)
[0039]
式中，rel3是选区元件阈值整定的可靠系数，lgκ
b(1)(max)
是区外故障产生的1模电压反行波的最大曲率对数值；
[0040]
步骤五：计算1模电压积分、0模电压积分，进行选极元件判别，若任意判据满足，则判别为对应的极故障类型，保护出口，否则返回步骤一；
[0041]
选极元件的判别式如式(12)所示，
[0042][0043]
式中，intg_u
(1)
(k)和intg_u
(0)
(k)为别是第k个采样时刻对应的1模电压故障分量和0模电压故障分量的积分值，计算方式如式(13)所示，ε4和ε5是选极元件的阈值，其整定原则如式(14)所示，
[0044][0045]
式中，δu
(0)
(k-j)为第k个采样时刻对应的0模电压故障分量，δu
(1)
(k-j)第k个采样时刻对应的1模电压故障分量；
[0046][0047]
式中，rel4和rel5是选极元件阈值整定的可靠系数，intg_u
(0)(max)
和intg_u
(0)(max)
是稳态阶段0模电压波动和1模电压波动产生的最大积分值。
[0048]
优选的，启动元件阈值整定的可靠系数rel1、方向元件阈值整定可靠系数rel2、选区元件阈值整定的可靠系数rel3、选极元件阈值整定的可靠系数rel4和rel5，取值均为1.1
～1.2。
[0049]
本发明和现有技术相比较，具备如下优点：
[0050]
由于曲率随过渡电阻的增大而增大，本发明具有较强的耐受过渡电阻的能力；由于曲率对频率变化的敏感度低且算法简单，本发明对采样频率和计算能力的要求低；由于曲率可以解析表达，本发明的阈值整定可以消除对仿真数据的依赖。综上，本发明对故障的快速隔离和保障电力系统的安全稳定运行有着重要的现实意义。
附图说明
[0051]
图1是适用于本发明方法的一种直流系统拓扑图。
[0052]
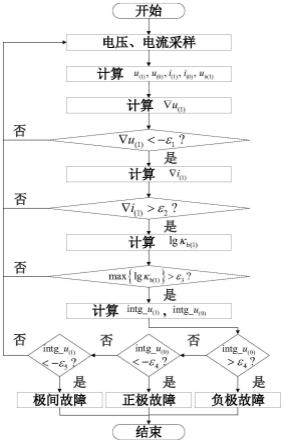
图2是本发明方法的流程图。
[0053]
图3(a)是一种直流线路故障下的线路正极电压波形。
[0054]
图3(b)是一种直流线路故障下的线路负极电压波形。
[0055]
图3(c)是一种直流线路故障下的线路正极电流波形。
[0056]
图3(d)是一种直流线路故障下的线路负极电流波形。
[0057]
图4(a)是基于本发明方法判别的启动元件动作信号。
[0058]
图4(b)是基于本发明方法判别的方向元件动作信号。
[0059]
图4(c)是基于本发明方法判别的选区元件动作信号。
[0060]
图4(d)是基于本发明方法判别的选极元件动作信号。
[0061]
图4(e)是基于本发明方法判别的主保护动作信号。
具体实施方式
[0062]
下面结合附图和实施例对本发明做进一步详细说明。如图1所示，系统正极输电线路中点发生金属性接地故障(记为故障f1)。
[0063]
当系统发生故障f1后，采样元件测得的电压和电流波形如图3(a)、图3(b)、图3(c)和图3(d)所示，基于本发明方法判别的保护元件动作信号如图4(a)、图4(b)、图4(c)、图4(d)和图4(e)所示。
[0064]
一种基于反行波曲率的柔性直流输电线路保护方法，其流程如图2所示，包括以下步骤：
[0065]
步骤一：采样正极电压u
p
，负极电压un，正极电流i
p
，负极电流in，结果如图2所示。
[0066]
根据式(1)计算1模电压u
(1)
、0模电压u
(0)
、1模电流i
(1)
、0模电流i
(0)
。
[0067]
根据式(3)，由1模电压u
(1)
、1模电流i
(1)
计算1模电压反行波u
b(1)
。
[0068]
步骤二：根据式(4)计算1模电压梯度结果为-1.0782p.u.。
[0069]
根据式(5)整定阈值ε1，其中，可靠系数rel1取为1.2，稳态阶段电压波动产生的最大梯度计算结果为0.071p.u.，ε1整定为0.085p.u.。
[0070]
根据式(4)进行启动元件判别，判据满足，判定为故障，继续执行。
[0071]
步骤三：根据式(6)计算1模电流梯度结果为0.5431p.u.。
[0072]
根据式(7)整定阈值ε2，其中，可靠系数rel2取为1.2，稳态阶段电流波动产生的最
大梯度计算结果为0.071p.u.，ε2整定为0.085p.u.。
[0073]
根据式(6)进行方向元件判别，判据满足，判定为正向故障，继续执行。
[0074]
步骤四：根据式(9)计算1模电压反行波的一次导数u
′
b(1)
，1模电压反行波的二次导数u
″
b(1)
，根据式(8)计算1模电压反行波的曲率κ
b(1)
。
[0075]
根据式(10)整定阈值ε3，其中，可靠系数rel3取为1.2，区外故障产生的1模电压反行波的最大曲率对数值lgκ
b(1)(max)
计算结果为-1.30，ε3整定为-1.56。
[0076]
根据式(11)进行选区元件判别，判据满足，判定为区内故障，继续执行。
[0077]
步骤五：根据式(13)计算1模电压积分intg_u
(1)
，结果为-0.5365p.u.
·
ms，计算0模电压积分intg_u
(0)
，结果为-0.3736p.u.
·
ms。
[0078]
根据式(14)整定阈值ε4，其中，可靠系数rel4取为1.2，稳态阶段0模电压波动产生的最大积分值intg_u
(0)(max)
计算结果为0.035p.u.
·
ms，ε4整定为0.042p.u.
·
ms。
[0079]
根据式(14)整定阈值ε5，其中，可靠系数rel5取为1.2，稳态阶段1模电压波动产生的最大积分值intg_u
(1)(max)
计算结果为0.035p.u.
·
ms，ε5整定为0.042p.u.
·
ms。
[0080]
根据式(12)进行选极元件判别，判据满足正极接地故障，正极线路保护出口，流程结束。
[0081]
从图4(a)、图4(b)、图4(c)、图4(d)和图4(e)可以看出：该保护方法能够可靠的识别故障并发出正确的动作信号，且保护动作的时间短。