一种应用于高速ADC的LMS误差校正系统及方法与流程

本发明涉及一种应用于高速ADC的LMS误差校正系统及方法。

背景技术：

随着集成电路工艺的进步，数字自适应校正技术(简称LMS)被广泛的应用于解决ADC中的各类偏差问题，LMS算法是对初始化的滤波器系数依据最小均方误差准则进行不断修正来实现的，LMS算法有一个收敛时间，这个时间受到算法步长因子的控制，在一定值范围内，增大步长因子会减小收敛时间，但是稳定后跟踪精度较低,反之则调整时间更长,稳定后跟踪精度更高。

对ADC当中运算放大器的增益误差校正是LMS算法的一个典型应用。由于运算放大器的增益误差的校正常常需要千分之一的精度，所以LMS算法的步长因子通常是一个很小的值，比如处于10^-12级别，至少需要41比特小数才能以有符号数的形式表达这个步长因子，因此在具体运算时数据的位宽非常大，难以在高速电路当中进行实现。随着近年来高速ADC电路的发展，急需一种可以在高速ADC当中实现误差校正LMS算法的电路及方法。

技术实现要素：

本发明的目的在于克服现有技术的不足，提供一种应用于高速ADC的LMS误差校正系统及方法。

本发明的目的是通过以下技术方案来实现的：一种应用于高速ADC的LMS误差校正系统，包括串并转换电路、并行运算电路和结果生成电路；所述的串并转换电路的输出端与并行运算电路连接，并行运算电路的输出端与结果生成电路连接；串并转换电路用于将ADC的采样输入信号和采样输出信号进行串并转换，得到多路的ADC采样输入信号和ADC采样输出信号，并行运算电路用于将串并转换得到的信号进行并行运算，结果生成电路接收并行运算电路的输出做进一步处理，并实现误差校正信号的输出。

所述的并行运算电路包括多个并行运算支路，每个并行运算支路对应于一路ADC采样输入信号和ADC采样输出信号；每个并行运算支路的输出端均与结果生成电路连接。

所述并行运算支路包括ADC采样输入信号并行输入端、采样输出信号并行输入端、第一运算输出端、第二运算输出端和四个乘法器；

第一乘法器的两路输入端分别与ADC采样输入信号并行输入端和采样输出信号并行输入端连接，第一乘法器的输出端与第三乘法器的一路输入端连接，第三乘法器的另一路输入端连接信号u，第三乘法器的输出端与第一运算输出端连接；

第二乘法器的两路输入端均与采样输出信号并行输入端连接，第二乘法器的输出端与第四乘法器的一路输入端连接，第四乘法器的另一路输入端连接信号u，第四乘法器的输出端与第二运算输出端连接。

所述的结果生成电路包括加法器一、加法器二、加法器三、减法器、D触发器一、D触发器二、D触发器三、除法器和第五乘法器；所述加法器一的输入端分别与每个并行运算支路的第一运算输出端连接，加法器一的输出端通过D触发器一与加法器三的第一路输入端连接；所述加法器二的输入端分别与每个并行运算支路的第二运算输出端连接，加法器二的输出端与减法器的负输入端连接，减法器的正输入端接1*2^exp信号，减法器的输出端与D触发器二连接，D触发器二的输出端与第五乘法器的第一路输入端连接，第五乘法器的第二路输入端与D触发器三的输出端连接，第五乘法器的输出端与加法器三的第二路输入端连接，加法器三的输出端与除法器连接，该除法器除数固定，除法器输出端既与D触发器三输入端连接，同时也与结果生成电路的输出端连接，作为最终的LMS误差校正信号。

所述结果生成电路中，第五乘法器的第二路输入端输入的信号w[kM]表示误差跟踪信号,由上一次最终输出的LMS误差校正信号通过D触发器三处理得到,。

所述的一种应用于高速ADC的LMS误差校正系统的校正方法，包括以下步骤：

S1.获取ADC的采样输入信号d[n]和采样输出信号x[n]；

S2.将信号d[n]和信号x[n]进行串并转换，并在每个并行运算支路中结合信号u对串并转换得到的信号进行运算，u代表步长因子科学计数法的有效位，即将LMS运算的步长因子u*2^-exp放大2^exp倍即可得到u；

S3.将每个并行运算支路中第一运算输出端的信号相加，得到p_res_sum[kM]，将每个并行运算支路的第二输出端信号相加，并通过减法器处理，得到信号s_res_sum[kM]；

S4.将p_res_sum[kM]通过D触发器一的处理后得到信号P1；将s_res_sum[kM]通过D触发器二处理后，与w[kM]相乘得到信号P2，将信号P1与信号P2相加，由于在生成s_res_sum[kM]和p_res_sum[kM]的运算中，步长因子均被放大2^exp倍，所以得到最终输出的LMS误差校正信号也被放大2^exp倍，即输出结果为w[(k+1)M]*2^exp：

w[(k+1)M]*2^exp＝w[kM]*s_res_sum[kM]+p_res_sum[kM]；

S5.将加法器三的结果w[(k+1)M]*2^exp通过右移的方式进行除法运算后，得到最终输出信号w[(k+1)M]。

所述的步骤S2包括以下子步骤：

S21.将信号d[n]进行串并转换，得到d[kM]、d[kM+1]、….d[kM+m]…d[kM+M-1]；其中m为0到M-1之间的整数，M表示串并转换得到的信号个数，即并行运算的支路个数；

S22.将信号x[n]进行串并转换，得到x[kM]、x[kM+1]、….x[kM+m]…x[kM+M-1]；其中m为0到M-1之间的整数，M表示串并转换得到的信号个数，即并行运算的支路个数；

S23.在并行运算电路的每个支路中，结合信号u对串并转换得到的信号进行运算，从每个并行运算支路的第一运算输出端和第二运算输出端输出运算结果，其中u代表步长因子科学计数法的有效位，实现将LMS运算的步长因子u*2^-exp放大2^exp倍，-exp为幂指数。

所述的步骤S3包括以下子步骤：

S31.将每个并行运算支路中第一运算输出端的信号通过第一加法器相加，得到p_res_sum[kM]，由于在并行运算支路中采用步长因子科学计数法的有效位u进行运算，故LMS运算的步长因子u*2^-exp实际上被放大了2^exp倍，只有有效位u参与运算，得到的信号实际上放大了2^exp倍：

$p\_res\_sum\[kM\]=\frac{u}{M}*\underset{m=0}{\overset{m=M-1}{\Σ}}d\[kM+m\]*x\[kM+m\];$

S32.将每个并行运算支路的第二输出端信号通过第二加法器相加，得到的信号同样放大了2^exp倍，并通过减法器运算，由于减数被放大2^exp倍，因此被减数也需要放大同样倍数，因此需要用1*2^exp减去相加得到的信号，获得s_res_sum[kM]：：

$s\_res\_sum\[kM\]=1*2^{\exp }-\frac{u}{M}*\underset{m=0}{\overset{m=M-1}{\Σ}}{x}^2\[kM+m\].$

所述的w[kM]由上一次最终输出的LMS误差校正信号w[(k+1)M]通过D触发器三处理得到。

进一步地，在公式w[(k+1)M]*2^exp＝w[kM]*s_res_sum[kM]+p_res_sum[kM]中，实际上运算放大结果扩大了2^exp倍；本申请中最终的输出结果需要除以2^exp，或者通过乘以2^-exp，通过右移以抵消这种放大。

本发明的有益效果是：本发明先通过串并转换电路进行转换，再通过并行运算电路及结果生成电路进行计算，所有变量的数据率都比原始输入数据率降低了M倍，同时并行运算电路可根据电路的实现速度进行相应的流水线运算，从而避免了运算量最大的这一部分成为制约系统实现速度的瓶颈。

附图说明

图1为LMS算法校正ADC电路运放增益的应用框图；

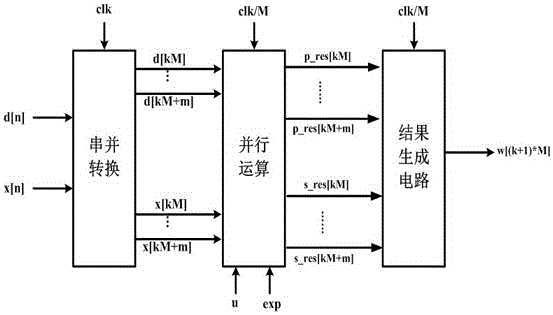
图2为本发明的原理框图；

图3为并行运算电路及结果生成电路的具体电路图。

具体实施方式

下面结合附图进一步详细描述本发明的技术方案，但本发明的保护范围不局限于以下所述。

如图1所示，使用LMS算法校正ADC电路运放增益的应用框图，通过在ADC的输入端加入确知的信号d[n]，再将ADC的输出x[n]与d[n]进行相关运算，可以计算出图中的opamp_gain值，即运放增益。

如图2所示，一种应用于高速ADC的LMS误差校正系统，包括串并转换电路、并行运算电路和结果生成电路；所述的串并转换电路的输出端与并行运算电路连接，结果生成电路的输出端与并行运算电路连接；串并转换电路用于将ADC的输入采样信号和采样输出信号进行串并转换，得到多路的ADC采样输入信号和ADC采样输出信号，并行运算电路用于将串并转换得到的信号进行并行运算，结果生成电路接收并行运算电路的输出做进一步处理，并实现误差校正信号的输出。

本申请中由于高速ADC电路的数据率通常为几百MHz甚至GHz以上，LMS算法当中大量高位宽的数据运算无法直接实现如此之高的数据吞吐率，所以必须引入串并转换电路，将输入数据率降低。

如图3所示，所述的并行运算电路包括多个并行运算支路，每个并行运算支路对应于一路ADC采样输入信号和ADC采样输出信号；每个并行运算支路的输出端均与结果生成电路连接。

所述并行运算支路包括ADC采样输入信号并行输入端、采样输出信号并行输入端、第一运算输出端、第二运算输出端和四个乘法器；

第一乘法器的两路输入端分别与ADC采样输入信号并行输入端和采样输出信号并行输入端连接，第一乘法器的输出端与第三乘法器的一路输入端连接，第三乘法器的另一路输入端连接信号u，第三乘法器的输出端与第一运算输出端连接；

第二乘法器的两路输入端均与采样输出信号并行输入端连接，第二乘法器的输出端与第四乘法器的一路输入端连接，第四乘法器的另一路输入端连接信号u，第四乘法器的输出端与第二运算输出端连接。

所述的结果生成电路包括加法器一、加法器二、加法器三、减法器、D触发器一、D触发器二、D触发器三、除法器和第五乘法器；所述加法器一的输入端分别与每个并行运算支路的第一运算输出端连接，加法器一的输出端通过D触发器一与加法器三的第一路输入端连接；所述加法器二的输入端分别与每个并行运算支路的第二运算输出端连接，加法器二的输出端与减法器的负输入端连接，减法器的正输入端接1*2^exp信号，减法器的输出端与D触发器二连接，D触发器二的输出端与第五乘法器的第一路输入端连接，第五乘法器的第二路输入端与D触发器三的输出端连接，乘法器的输出端与加法器三的第二路输入端连接，加法器三的输出端与除法器连接，该除法器除数固定(除数为2^exp)，除法器输出端既与D触发器三输入端连接，同时也与结果生成电路的输出端连接，作为最终的LMS误差校正信号。

从图3可以看出，每一个并行运算支路分别计算当前输入所对应的p_res变量和s_res变量，并行运算支路的输入数据率为原始数据率的M分之一，所以p_res变量和s_res变量的运算速度可以大幅度降低，方便电路实现。

所述结果生成电路中，第五乘法器的第二路输入端输入的信号w[kM]由上一次最终输出的LMS误差校正信号通过D触发器三处理得到。

所述的一种应用于高速ADC的LMS误差校正系统的校正方法，包括以下步骤：

S1.获取ADC的采样输入信号d[n]和采样输出信号x[n]；

S2.将信号d[n]和信号x[n]进行串并转换，并在每个并行运算支路中结合信号u对串并转换得到的信号进行运算，u代表步长因子科学计数法的有效位，即将LMS运算的步长因子u*2^-exp放大2^exp倍即可得到u；

S3.将每个并行运算支路中第一运算输出端的信号相加，得到p_res_sum[kM]，将每个并行运算支路的第二输出端信号相加，并通过减法器处理，得到信号s_res_sum[kM]；

S4.将p_res_sum[kM]通过D触发器一的处理后得到信号P1；将s_res_sum[kM]通过D触发器二处理后，与w[kM]相乘得到信号P2，将信号P1与信号P2相加，由于在生成s_res_sum[kM]和p_res_sum[kM]的运算中，步长因子均被放大2^exp倍，所以得到最终输出的LMS误差校正信号也被放大2^exp倍，即输出结果为w[(k+1)M]*2^exp：

w[(k+1)M]*2^exp＝w[kM]*s_res_sum[kM]+p_res_sum[kM]；

S5.将加法器三的结果w[(k+1)M]*2^exp通过右移的方式进行除法运算后，得到最终输出信号w[(k+1)M]。

其中s_res_sum[kM]和p_res_sum[kM]与w[kM]无关，可根据输入数据提前进行独立运算，即通过并行运算支路结合结果生成电路中的加法器实现。

所述的步骤S2包括以下子步骤：

S21.将信号d[n]进行串并转换，得到d[kM]、d[kM+1]、….d[kM+m]…d[kM+M-1]；其中m为0到M-1之间的整数，M表示串并转换得到的信号个数，即并行运算的支路个数；

S22.将信号x[n]进行串并转换，得到x[kM]、x[kM+1]、….x[kM+m]…x[kM+M-1]；其中m为0到M-1之间的整数，M表示串并转换得到的信号个数，即并行运算的支路个数；S23.在并行运算电路的每个支路中，结合信号u对串并转换得到的信号进行运算，从每个并行运算支路的第一运算输出端和第二运算输出端输出运算结果；其中u代表步长因子科学计数法的有效位，实现将LMS运算的步长因子u*2^-exp放大2^exp倍，-exp为幂指数。

所述的步骤S3包括以下子步骤：

S31.将每个并行运算支路中第一运算输出端的信号通过第一加法器相加，得到p_res_sum[kM]，由于在并行运算支路中采用步长因子科学计数法的有效位u进行运算，故LMS运算的步长因子u*2^-exp实际上被放大了2^exp倍，只有有效位u参与运算，得到的信号也放大了2^exp倍：

$p\_res\_sum\[kM\]=\frac{u}{M}*\underset{m=0}{\overset{m=M-1}{\Σ}}d\[kM+m\]*x\[kM+m\];$

S32.将每个并行运算支路的第二输出端信号通过第二加法器相加，得到的信号同样放大了2^exp倍，并通过减法器运算，由于减数被放大2^exp倍，因此被减数也需要放大同样倍数，用1*2^exp减去相加得到的信号，获得s_res_sum[kM]：

$s\_res\_sum\[kM\]=1*2^{\exp }-\frac{u}{M}*\underset{m=0}{\overset{m=M-1}{\Σ}}{x}^2\[kM+m\].$

所述的w[kM]由上一次最终输出的LMS误差校正信号w[(k+1)M]通过D触发器三处理得到。

进一步地，在公式w[(k+1)M]*2^exp＝w[kM]*s_res_sum[kM]+p_res_sum[kM]中，实际上运算放大结果扩大了2^exp倍；本申请中最终的输出结果需要除以2^exp，或者通过乘以2^-exp，通过右移以抵消这种放大。