一种基于改进StOMP的压缩感知重构算法的制作方法

技术领域：

本发明涉及无线通信领域，尤其涉及压缩感知领域中一种基于stomp的改进压缩感知重构算法。

背景技术：
：

压缩感知理论是一种新兴的信号压缩采样技术。该理论中的核心问题是信号的重构问题，常用的重构方法主要有贪婪追踪算法、凸松弛算法和组合算法这三大类。贪婪追踪算法由于算法结构简单、计算量小等优点备受关注，而正交匹配追踪(orthogonalmatchingpursuit，omp)类算法为其主流，更成为研究者研究的重点，国内外许多研究者对此类算法进行了研究与改进。

贪婪追踪算法是通过贪婪迭代的方法来更新支撑集，逐步逼近原始解，目前常用的贪婪算法有omp算法、分段正交匹配追踪(stagewiseorthogonalmatchingpursuit，stomp)算法、正则化正交匹配追踪(regularizedorthogonalmatchingpursuit，romp)算法、压缩采样匹配追踪(compressivesamplingmatchingpursuit，cosamp)算法、子空间追踪(subpuistpursuit，sp)算法、稀疏度自适应匹配追踪(sparsityadaptivematchingpursuit，samp)算法等。

stomp算法因每次迭代根据阈值选择得到的是多个匹配原子而不是单个原子，减少了迭代次数，相对于omp算法进行了一定程度的简化，使运行时间为常用匹配算法里较少的一种，且它不需要知道稀疏度。由于并没有运用稀疏度这一先验信息，且原子的选择跟阈值设置紧密相关，固其重构精度不够理想。

sp算法在omp的基础上，引入回溯思想，为了提高算法的收敛速度和算法效率，通过回溯的思想从原子库里选择多个相关原子同时剔除部分不相关原子，在每次迭代中保证了原子的可信赖度；但其对稀疏度依赖性大，若错误估计了稀疏度的值，算法精确重构的能力会下降。

romp算法在omp的基础上改进了原子的选择标准，通过正则化过程对原子进行了二次选择。它结合了贪婪算法的速度和凸优化方法的强有力的理论保证，给出了不同终止准则下的重构误差的上限。romp算法的运行时间与omp算法的运行时间在理论上是相当的，且需要估计稀疏度，但它具有较高的重构精度。

综上，对于现在已经出现的压缩感知重构算法，均存在重构精度低或复杂度高的问题，这就亟需本领域技术人员解决相应的技术问题。

技术实现要素：
：

本发明旨在至少解决现有技术中存在的技术问题，特别创新地提出了一种基于改进stomp的压缩感知重构算法。

为了实现本发明的上述目的，本发明提供了一种基于改进stomp的压缩感知重构算法，其特征在于，包括：

s1，基于分段正交匹配追踪算法，根据阈值大小选择执行回溯原子选择算法或romp算法。

s2，引入子空间正交匹配追踪算法的回溯思想，即回溯原子选择算法，使每次选择的原子个数等于分段正交匹配追踪算法中选出的列数。

s3，将回溯原子选择算法和romp嵌入stomp中，根据相邻两次重构信号能量差判断是否进行算法转换或者迭代停止。

所述的一种基于改进stomp的压缩感知重构算法，其特征在于，所述s1包括：

考虑原信号且为可稀疏信号，根据压缩感知理论，将其投影到稀疏基空间上可表示为：

x＝ψθ

其中，为稀疏系数，含有k个非零元素，则称原信号x是k稀疏的；为信号x的稀疏基。

选择随机高斯矩阵作为观测矩阵φ，其内元素均满足高斯分布n(0,1/n)，则n维信号可由m个观测值表示：

y＝φx＝φψθ＝aθ

其中，是信号的观测值，为传感矩阵。

令r0＝y，并以h＝β×max(th)作为判断标准，确定下一步执行回溯原子选择算法或romp算法，其中th＝tsσs，根据经验值取ts＝2.5，1/n为高斯观测矩阵中元素所服从的高斯分布的方差。则

根据stomp，以rt表示残差，t表示迭代次数，表示空集，jo表示每次迭代找到的列序号，λt表示t次迭代的列序号集合，aj表示矩阵a的第j列，at表示按索引λt选出的传感矩阵a的列集合。

首先计算u＝<rt-1,aj>,1≤j≤n，选u中大于阈值th＝tsσs的c列，并记对应的a列序号j构成集合jo；然后，令λt＝λt-1∪jo，at＝at-1∪aj(j∈jo)。再则令ts＝2.5，判断th＝tsσs与h的大小关系后，选择执行回溯原子选择算法或romp算法。

当th＞h时，将stomp选出的at执行回溯原子选择算法；

当th＜h时，将stomp选出的at执行romp算法。

所述的一种基于改进stomp的压缩感知重构算法，其特征在于，所述s2包括：

当th＞h时，将stomp选出的at执行回溯原子选择算法，引入回溯思想，确保原子可靠性，选出的稀疏系数估计值个数等于分段正交匹配选出的原子列数c。

首先，求y＝atθt的最小二乘解：为第t次迭代估计得到的稀疏系数；再从中选出绝对值最大的c项，记为对应的at中的c列记为atc，对应的列序号记为λtc，更新集合λt＝λtc；其次，更新残差利用稀疏矩阵可得重构信号：

所述的一种基于改进stomp的压缩感知重构算法，其特征在于，所述s3包括：

将回溯原子选择算法和romp嵌入stomp中，根据相邻两次重构信号能量差的大小确定算法的转换或迭代的停止。

在stomp中，阈值th是残差的函数，随迭代过程中残差的变小而变小，则以阈值th反映重构的进度。

当残差值较大，满足th＞h时，迭代得到的重构信号离目标值较远，此时执行回溯原子选择算法，迭代一次得到c个有效原子，迭代至相邻两次重构信号的能量差小于ε1时停止执行回溯原子选择算法，转而执行romp算法。

当残差值较小，满足th＜h时，迭代得到的重构信号较靠近目标值，此时选择romp算法，迭代一次得到不大于c个有效原子，迭代至相邻两次重构信号的能量差小于ε2时，停止迭代，并输出重构信号作为最终结果。

当th＞h时，执行回溯原子选择算法；迭代至相邻两次重构得到的信号能量差满足：时，停止执行回溯原子选择算法转而执行romp算法。

当th＜h时，执行romp算法，对原子进行正则化；首先，构建子空间，使其内的元素满足：选择所有满足要求的子集j中具有最大能量者，即选择其次，令λt＝λt-1∪jo，at＝at-1∪aj(j∈jo)；然后，更新残差则可利用稀疏矩阵可得重构信号：

进入romp算法后，迭代直到相邻两次重构信号能量差满足时，停止迭代，输出重构信号。

本发明通过改进stomp压缩感知重构算法，有效地利用阈值判断标准保证算法收敛速度和精度，同时将相邻两次重构信号的能量差作为算法转化依据和停止迭代的依据，结合了回溯原子选择算法收敛速度快和romp算法重构精度高的优点，实现重构精度和收敛速度的折中。

附图说明

本发明的上述和/或附加的方面和优点从结合下面附图对实施例的描述中将变得明显和容易理解，其中：

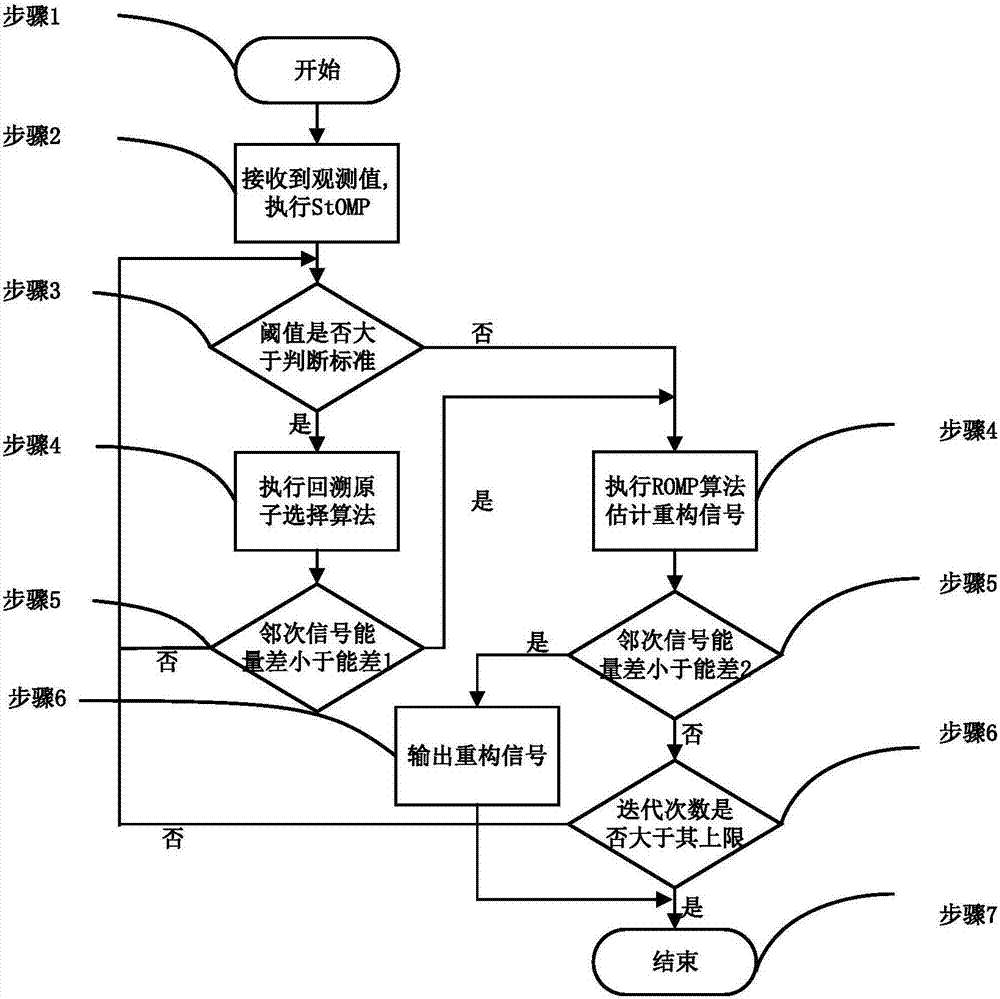
图1是本发明总体流程图。

具体实施方式

下面详细描述本发明的实施例，所述实施例的示例在附图中示出，其中自始至终相同或类似的标号表示相同或类似的元件或具有相同或类似功能的元件。下面通过参考附图描述的实施例是示例性的，仅用于解释本发明，而不能理解为对本发明的限制。

在本发明的描述中，需要理解的是，术语“纵向”、“横向”、“上”、“下”、“前”、“后”、“左”、“右”、“竖直”、“水平”、“顶”、“底”“内”、“外”等指示的方位或位置关系为基于附图所示的方位或位置关系，仅是为了便于描述本发明和简化描述，而不是指示或暗示所指的装置或元件必须具有特定的方位、以特定的方位构造和操作，因此不能理解为对本发明的限制。

在本发明的描述中，除非另有规定和限定，需要说明的是，术语“安装”、“相连”、“连接”应做广义理解，例如，可以是机械连接或电连接，也可以是两个元件内部的连通，可以是直接相连，也可以通过中间媒介间接相连，对于本领域的普通技术人员而言，可以根据具体情况理解上述术语的具体含义。

本发明提出了一种基于改进stomp的压缩感知重构算法，有效地将回溯原子选择算法和romp嵌入stomp中，基于stomp收敛速度快的优点，利用stomp的阈值大小标准将重构过程分为两个阶段：重构初始阶段，即离目标值较远时执行回溯原子选择算法，引入回溯思想提高原子可靠性；重构过程末端，即接近目标值阶段的利用omp进行高精度逼近，实现重构算法收敛速度和精度的有效结合。

结合附图1对本发明进行详细说明，主要包括以下步骤：

步骤1：开始。

步骤2：接收到观测值，开始执行stomp。

考虑原信号且为可稀疏信号，根据压缩感知理论，选择随机高斯矩阵作为观测矩阵φ，其内元素均满足高斯分布n(0,1/n)，则n维信号可由m个观测值表示：

y＝φx＝φψθ＝aθ

其中，为稀疏系数，其中含有k个非零元素，则称原信号x是k稀疏的。为信号x的稀疏基，是信号的观测值，为传感矩阵。

根据stomp，以rt表示残差，t表示迭代次数，表示空集，jo表示每次迭代找到的列序号，λt表示t次迭代的列序号集合，aj表示矩阵a的第j列，at表示按索引λt选出的传感矩阵a的列集合。

首先计算u＝<rt-1,aj>,1≤j≤n，选择u中大于阈值th＝tsσs的c列，并记下这些值对应a的列序号j构成集合jo。接着，令λt＝λt-1∪jo，at＝at-1∪aj(j∈jo)。

步骤3：确定阈值大小判断标准，选择下一步执行回溯原子选择算法或romp算法。

令r0＝y，并将作为阈值大小的判断标准，选择算法即：

取ts＝2.5，判断th＝tsσs与h的大小关系后，选择相应的下一步算法：

当th＞h时，将步骤2选出的at执行回溯原子选择算法；

当th＜h时，将步骤2选出的at执行romp算法。

步骤4：执行回溯原子选择算法或romp算法。

当th＞h时，将步骤2中选出的at执行回溯原子选择算法，引入回溯思想保证原子可靠性：

首先，求y＝atθt的最小二乘解：为第t次迭代估计得到的稀疏系数。再从中选出绝对值最大的c项，记为对应的at中的c列记为atc，对应的列序号记为λtc，更新集合λt＝λtc。然后，更新残差且迭代次数t＝t+1。利用稀疏矩阵可得重构信号：

当th＜h时，将步骤2选出的at执行romp算法。

首先，构建子空间，使其内的元素满足：选择所有满足要求的子集j中具有最大能量者，即选择接着，更新列序号集合及a的列构成的集合，即λt＝λt-1∪jo,at＝at-1∪aj(j∈jo)，然后，更新残差且迭代次数t＝t+1。则可利用稀疏矩阵可得重构信号：

步骤5：判断对应的停止条件，进行算法转换或停止。

取迭代次数的经验值s＝10，ε2＝0.2ε1。

当th＞h时，执行回溯原子选择算法，迭代至相邻两次重构得到的信号能量差满足：时，停止执行回溯原子选择算法转而执行romp算法。

进入romp算法后，迭代直到相邻两次重构信号能量差满足时，停止迭代，执行步骤7。

步骤6：判断是否迭代次数t是否大于s＝10，大于则执行步骤8，否则执行步骤2。

步骤7：输出重构信号

步骤8：结束。

在本说明书的描述中，参考术语“一个实施例”、“一些实施例”、“示例”、“具体示例”、或“一些示例”等的描述意指结合该实施例或示例描述的具体特征、结构、材料或者特点包含于本发明的至少一个实施例或示例中。在本说明书中，对上述术语的示意性表述不一定指的是相同的实施例或示例。而且，描述的具体特征、结构、材料或者特点可以在任何的一个或多个实施例或示例中以合适的方式结合。

尽管已经示出和描述了本发明的实施例，本领域的普通技术人员可以理解：在不脱离本发明的原理和宗旨的情况下可以对这些实施例进行多种变化、修改、替换和变型，本发明的范围由权利要求及其等同物限定。