一种超宽带白噪声实现方法与流程

1.本发明提供一种超宽带白噪声实现方法，本发明可以实现数百兆带宽白噪声的产生，可广泛应用于电子对抗、干扰模拟器和电磁环境模拟等应用场景。


背景技术：

2.白噪声的常见方法有m序列白噪化和box-muller算法，这两种都能产生效果相当不错的白噪声，但是当白噪声带宽要求非常宽时，box-muller和m序列白噪化方法都很难进行高速多相实现。所以需要进行改进。
3.《一种基于fpga的高斯白噪声发生器》(分类号：h03b29/00(2006.01)i)描述的box-muller变形算法，很难并行实现产生超宽带的白噪声。
4.《数字式话音级高斯白噪声发生器》(分类号：cn101907715a)采用m序列结合wallace算法的方式，虽然m序列高速并行化实现简单，但是wallace并行化实现很困难，所以也很难生成超宽带的白噪声。


技术实现要素：

5.本发明的目的在于提供一种超宽带白噪声的实现方法。
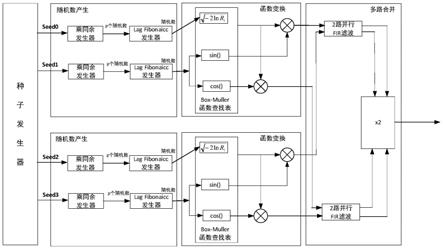
6.本发明提出的一种超宽带白噪声的实现方法，所述实现方法由超宽带白噪声的实现系统完成，所述系统由种子发生器、随机数产生模块、函数变化模块和多路合并模块组成；其中：
7.种子发生器分成四路，分别连接两路随机数产生模块，随机数产生模块由乘同余发生器模块和lag fibonaicc发生器模块组成，乘同余发生器的输出端连接lag fibonaicc发生器模块的输入端，产生iq(各两路，共4路)的均匀分布信号；
8.两路随机数产生模块的输出端分别连接两路函数变化模块的输入端，通过改进的box-muller法完成均匀噪声的白噪声化，两路函数变化模块的输出端分别连接多路合并模块；
9.多路合并模块通过改进的多相并行滤波的方式实现多路合并，最终形成超宽带的白噪声信号；所述实现方法具体步骤如下：
10.(1)由种子发生器随机产生四个能产生具有较好非相关性的随机数种子分别送给两路随机数产生模块作为四个种子输入；
11.(2)两路随机数产生模块收到四路种子后，每一路随机数产生模块均利用乘同余生成器模块和lag fibonaicc发生器模块的组合，生成均匀分布的四路随机数；
12.(3)两路函数变换模块根据收到的四路随机数，每一路函数变换模块均利用改进的box-muller法生成两路正交的iq高斯化数据；
13.(4)多路合并模块根据收到的两个两路正交高斯数据，利用改进的四相并行滤波实现结构，产生高带宽的白噪声数据。
14.本发明中，步骤(1)中所述四个种子即seed0，seed1，seed2和seed3，四路种子的选
取需满足如下条件：
15.seed0+seed2＝seed1+seed3＝m
ꢀꢀꢀ
(公式1)
16.其中：seed0，seed1，seed2和seed3分别为四个输入的种子，m为随机数产生模块中的被除数；
17.本发明中，步骤(2)中随机数产生模块利用乘同余发生器和lag fibonaicc发生器组合生成均匀分布的随机数；
18.当乘同余发生器接收到种子后根据公式2产生前p个随机数；
19.x
i+1
＝ax
i mod m,i≤p
ꢀꢀꢀ
(公式2)
20.其中：xi为第i个随机数，x
i+1
为第i+1个随机数，a为常量，m为被除数，p为乘同余发生器生成的随机数数量；
21.然后这p个数送至lag fibonaicc发生器，lag fibonaicc发生器根据前p个数利用公式3计算产生后面的随机数；
22.x
i+1
＝x
i-q
+x
i-p mod m,i》p
ꢀꢀꢀ
(公式3)
23.其中：x
i-q
为第i-q个随机数，x
i-p
为第i-p个随机数，x
i+1
为第i+1个随机数，a为常量，m为被除数，p和q为x
p
+xq+1为本原根，且p》q；p和q的取值影响产生随机数的质量。
24.本发明中，步骤(3)中所述函采用box-muller方法实现；
25.对于步骤(2)产生的两路均匀分布随机变量u1和u2，采用公式4计算：
[0026][0027]
其中：u1和u2为两路均匀分布随机数，xi和xq分别为每路函数变换模块输出的两路正交高斯化数据。
[0028]
本发明中，步骤(4)中所述多路合并模块中，采用并行的fir滤波器进行实现；
[0029]
并行滤波结构采用一种“分而治之”的处理方式，将“待卷积”的两个序列和按交叉数据分配的原则分为“相同数量”的若干个子序列，比如下面所示的二相分解；
[0030]
一个抽头个数为n的fir滤波器在时域的输入输出关系如下：
[0031][0032]
其中：x[n]为输入信号序列，h[n]为fir滤波器的抽头系数组成的序列，n为抽头数量，n为抽样时刻序列，k为当前抽样时刻；
[0033]
y[n]在z域可表示为：
[0034][0035]
其中：h(z)为h[n]的z域变换，x(z)为x[n]的z域变换，y(z)为y[n]的z域变换，n为抽头数量，n为抽样时刻序列；
[0036]
将x(z)分解为奇数部和偶数部两部分，如下表示：
[0037][0038]
其中：x[n]为输入信号序列，x(z)为x[n]的z域变换，x0(z2)和x1(z2)分别对应于x[2k]和x[2k+1]的z域变换；
[0039]
同理，将h(z)也按照奇数部和偶数部分解为：
[0040]
h(z)＝h0(z2)+z-1
h1(z2)
ꢀꢀꢀ
(公式8)
[0041]
其中：h0(z2)和h1(z2)分别对应于h[2k]和h[2k+1]的z域变换。子滤波器h0(z2)和h1(z2)的长度均为n/2；
[0042]
利用公式7和公式8重新计算y(z)如下：
[0043][0044]
其中：x0(z2)和x1(z2)分别对应于x[2k]和x[2k+1]的z域变换。h0(z2)和h1(z2)分别对应于h[2k]和h[2k+1]的z域变换，y0(z2)和y1(z2)分别为y[2k]和y[2k+1]的z变换；
[0045]
公式9即为并行fir滤波器的多项式分解表示，该该滤波运算在每一次的迭代中，能同时处理两个输入x[2k]和x[2k+1]，并同时产生输出y[2k]和y[2k+1]；
[0046]
公式9对应的实现结构，需要2n次乘法以及2(n-1)次加法；
[0047]
将公式9改写成：
[0048][0049]
其中：x0(z2)和x1(z2)分别对应于x[2k]和x[2k+1]的z域变换。h0(z2)和h1(z2)分别对应于h[2k]和h[2k+1]的z域变换，y0(z2)和y1(z2)分别为y[2k]和y[2k+1]的z变换；
[0050]
公式10中y0(z2)和y1(z2)中均出现了x0(z2)h0(z2)和x1(z2)h1(z2)，在硬件实现中可
以进行复用，这样的结构使用3n/2个乘法器，3(n/2-1)+4个加法器。
[0051]
本发明中，对4路并行的fir滤波器改进结构进行推导，设：
[0052][0053]
其中：x0,x1,x2,x3分别对应于x[4k],x[4k+1],x[4k+2],x[4k+3]的z域变换，h0,h1,h2,h3分别对应于h[4k],h[4k+1],h[4k+2],h[4k+3]的z域变换，y0,y1,y2,y3分别对应于y[4k],y[4k+1],y[4k+2],y[4k+3]的z域变换，x0′
,x1′
分别对应于x[4k]+x[4k+2],x[4k+1]+x[4k+3]的z域变换，h0′
,h1′
分别对应于h[4k]+h[4k+2],h[4k+1]+h[4k+3]的z域变换；
[0054]
进一步推导，得到：
[0055][0056]
其中：x0,x1,x2,x3分别对应于x[4k],x[4k+1],x[4k+2],x[4k+3]的z域变换，h0,h1,h2,h3分别对应于h[4k],h[4k+1],h[4k+2],h[4k+3]的z域变换，x0′
,x1′
分别对应于x[4k]+x[4k+2],x[4k+1]+x[4k+3]的z域变换，h0′
,h1′
分别对应于h[4k]+h[4k+2],h[4k+1]+h[4k+3]的z域变换；
[0057]
通过上述推导，得到4路并行fir滤波器。
[0058]
本发明的有益效果在于：
[0059]
(1)随机数产生部分利用乘同余法来解决了lag fibonaicc序列前p个数的选取问题，同时利用lag fibonaicc序列的高速、长周期、高维均匀性解决了乘同余法的周期短、强相关等缺点，可以获得质量更佳的均匀随机数；
[0060]
(2)函数变换模块box-muller算法中函数采用hsm实现方法使用较少存储资源获得同样精度；
[0061]
(3)多路并行模块采用改进的多相并行滤波减少了乘法器资源占用，支持高带宽高速实现。
附图说明
[0062]
图1是本发明的实现框图；
[0063]
图2是函数图形在在区间(0,1]绘图及分段，从图中可以看出在0和1附近函数呈现为极大的非线性，所以对于本函数的计算也不能采用传统的基于均匀地址的查
找表方法，因为对于高度非线性区域可能要使用非常小的分段才能达到线性区域的精度；
[0064]
图3是采用hsm方法仿真得到的函数图形；
[0065]
图4是多相滤波器的实现结构图：
[0066]
图5是两路并行fir滤波器实现结构；
[0067]
图6是改进的两路并行fir滤波器实现结构；
[0068]
图7是4路并行滤波的改进结构；
[0069]
图中标号：1为种子发生器，2为为乘同余发生器，3为lag fibonaicc发生器，4为函数变化模块，5为多项合并模块。
具体实施方式
[0070]
下面通过实施例结合附图进一步说明本发明。
[0071]
实施例1：
[0072]
图1是本发明实现的方框图，所述系统由两路随机数产生模块，两路函数变化模块和多项合并模块构成，随机数产生模块使用fabonicci算法产生iq(各两路，共4路)的均匀分布信号。函数变化模块，通过实现正弦和余弦，最终完成均匀噪声的白噪声化，最终再通过多相并行滤波的方式实现多路合并，形成超宽带的白噪声信号。
[0073]
(1)由种子发生器随机产生四个种子(即seed0，seed1，seed2和seed3)，分别送给两路随机数产生模块的四个输入；为了让产生的随机数具有较好的非相关性，四路种子的选取需满足如下条件：
[0074]
seed0+seed2＝seed1+seed3＝m
ꢀꢀꢀ
(公式1)
[0075]
其中：seed0，seed1，seed2和seed3分别为四个输入的种子，m为随机数产生模块中的被除数；
[0076]
(2)随机数产生模块利用乘同余发生器和lag fibonaicc发生器组合生成均匀分布的随机数。
[0077]
当乘同余发生器接收到种子后根据公式2产生前p个随机数。
[0078]
x
i+1
＝ax
i mod m,i≤p
ꢀꢀꢀ
(公式2)
[0079]
其中：xi为第i个随机数，x
i+1
为第i+1个随机数，a为常量，m为被除数，p为乘同余发生器生成的随机数数量；
[0080]
然后这p个数送至lag fibonaicc发生器。lag fibonaicc发生器根据前p个数利用公式3计算产生后面的随机数；
[0081]
x
i+1
＝x
i-q
+x
i-p mod m,i》p
ꢀꢀꢀ
(公式3)
[0082]
其中：x
i-q
为第i-q个随机数，x
i-p
为第i-p个随机数，x
i+1
为第i+1个随机数，a为常量，m为被除数，p和q为x
p
+xq+1为本原根，且p》q；p和q的取值影响产生随机数的质量；
[0083]
(3)函数变换模块用于实现对步骤(2)得到均匀分布的数据进行白噪声化。采用box-muller方法实现；
[0084]
对于步骤(2)产生的两路均匀分布随机变量u1和u2，采用公式4计算：
[0085]
[0086]
其中：u1和u2为两路均匀分布随机数，xi和xq分别为每路函数变换模块输出的两路正交高斯化数据；
[0087]
函数变化模块中cos和sin通过cordic算法很好实现，主要在于运算的实现。该函数是是一个复合函数，如图2所示，在0和1附近函数呈现为极大的非线性，所以对于本函数的计算也不能采用传统的基于均匀地址的查找表方法，因为对于高度非线性区域可能要使用非常小的分段才能达到线性区域的精度。复合函数基本上都可以分解成几个基本函数分级计算。但是这种方法对于用硬件来实现不仅会带来很大的延时和舍入误差，而且可能会让计算无法进行；
[0088]
故采用如下方法：把(0，1]分成两个区间：(0，0.5)和[0.5，1]。对(0，0.5)，用它的中点来分段，然后对(0，0.25)再用它的中点来分段。对[0.5，1]做同样的处理，如图2所示。这样在每个区间，可以用一条直线y＝ax+b逼近，即每个区间用2个系数a,b来代替，可以用查找表的方式来实现，查找表的长度是输入变量x的位数的一倍，而表中每个单元是a,b需要的位数之和。x的位数为32，所以表长为64bit，从仿真结果可计算a需要33位来表示，b需要31位来表示，如图3所示。图3中有两个重要的小模块：段地址模块和a,b系数查找表模块。对于段地址模块在使用一般的寻址方法需要更多资源，因为它涉及到32个1比特相加，速率非常低，并要用很多加法器，对32bit的输入至少要4级流水线。而采用直接寻址，这样不用加法器，只需要2级流水线。对于a,b系数查找表模块，要进行多次计算、仿真，检查结果的正确性和精度，以此决定每小区间的系数a,b。经过不断的仿真，达到如图4所示的效果；
[0089]
(4)多路合并模块，主要实现并行滤波的算法：通过前两个算法模块，实际上已经得到超宽带的白噪声，如果需要实现一定宽频率内的宽带噪声，需要对基带的白噪声进行滤波，由于是超宽带下的操作，所以需要并行滤波的方式，同时由于fir滤波器的有限长冲击响应的特点，所以采用并行的fir滤波器进行实现；
[0090]
并行滤波结构采用一种“分而治之”的处理方式，将“待卷积”的两个序列和按交叉数据分配的原则分为“相同数量”的若干个子序列，比如下面所示的二相分解；
[0091]
一个抽头个数为n的fir滤波器在时域的输入输出关系如下：
[0092][0093]
其中：x[n]为输入信号序列，h[n]为fir滤波器的抽头系数组成的序列，n为抽头数量，n为抽样时刻序列，k为当前抽样时刻；
[0094]
y[n]在z域可表示为：
[0095][0096]
其中：h(z)为h[n]的z域变换，x(z)为x[n]的z域变换，y(z)为y[n]的z域变换，n为抽头数量，n为抽样时刻序列；
[0097]
可以将x(z)分解为奇数部和偶数部两部分，如下表示：
[0098][0099]
其中：x[n]为输入信号序列，x(z)为x[n]的z域变换，x0(z2)和x1(z2)分别对应于x[2k]和x[2k+1]的z域变换；
[0100]
同理，可以将h(z)也按照奇数部和偶数部分解为：
[0101]
h(z)＝h0(z2)+z-1
h1(z2)
ꢀꢀꢀ
(公式8)
[0102]
其中：h0(z2)和h1(z2)分别对应于h[2k]和h[2k+1]的z域变换。子滤波器h0(z2)和h1(z2)的长度均为n/2；
[0103]
利用公式7和公式8重新计算y(z)如下：
[0104][0105]
其中：x0(z2)和x1(z2)分别对应于x[2k]和x[2k+1]的z域变换。h0(z2)和h1(z2)分别对应于h[2k]和h[2k+1]的z域变换，y0(z2)和y1(z2)分别为y[2k]和y[2k+1]的z变换；
[0106]
公式9即为并行fir滤波器的多项式分解表示，该该滤波运算在每一次的迭代中，能同时处理两个输入x[2k]和x[2k+1]，并同时产生输出y[2k]和y[2k+1]；
[0107]
图5给出了公式9对应的实现结构，需要2n次乘法以及2(n-1)次加法；
[0108]
将公式9改写成：
[0109][0110]
其中：x0(z2)和x1(z2)分别对应于x[2k]和x[2k+1]的z域变换。h0(z2)和h1(z2)分别对应于h[2k]和h[2k+1]的z域变换。y0(z2)和y1(z2)分别为y[2k]和y[2k+1]的z变换；
[0111]
公式10中y0(z2)和y1(z2)中均出现了x0(z2)h0(z2)和x1(z2)h1(z2)，在硬件实现中可
以进行复用，其实现结构如图6所示。这样的结构使用3n/2个乘法器，3(n/2-1)+4个加法器；
[0112]
同理，对4路并行的fir滤波器改进结构进行推导，设：
[0113][0114]
其中：x0,x1,x2,x3分别对应于x[4k],x[4k+1],x[4k+2],x[4k+3]的z域变换，h0,h1,h2,h3分别对应于h[4k],h[4k+1],h[4k+2],h[4k+3]的z域变换，y0,y1,y2,y3分别对应于
[0115]
y[4k],y[4k+1],y[4k+2],y[4k+3]的z域变换，x0′
,x1′
分别对应于
[0116]
x[4k]+x[4k+2],x[4k+1]+x[4k+3]的z域变换，h0′
,h1′
分别对应于
[0117]
h[4k]+h[4k+2],h[4k+1]+h[4k+3]的z域变换；
[0118]
进一步推导，得到：
[0119][0120]
其中：x0,x1,x2,x3分别对应于x[4k],x[4k+1],x[4k+2],x[4k+3]的z域变换，h0,h1,h2,h3分别对应于h[4k],h[4k+1],h[4k+2],h[4k+3]的z域变换，x0′
,x1′
分别对应于
[0121]
x[4k]+x[4k+2],x[4k+1]+x[4k+3]的z域变换，h0′
,h1′
分别对应于
[0122]
h[4k]+h[4k+2],h[4k+1]+h[4k+3]的z域变换；
[0123]
通过上述推导，可以得到4路并行fir滤波器改进结构如图7所示；
[0124]
如图6和图7所示，并行滤波结构采用多相分解的并行结构，大大提高了fir滤波器的吞吐率，输入的数据也经过多相分解，其速率和最终的滤波输出的采样速率一致，数据带宽可做到0.4倍的采样率，解决了基于内插的多相滤波结构带宽受限的缺陷；但并行滤波结构同时也增加了fpga资源的开销。二路并行滤波结构需要进行2k次乘法和2k次加法操作，硬件资源开销是传统数字fir结构的2倍；四路并行滤波结构需要进行6k次乘法和6k+8次加法操作，硬件资源开销是传统数字fir结构的6倍。