一种适合无线分布式感知系统的数据处理方法及系统与流程

本发明涉及数据处理方法及系统，尤其涉及一种适合无线分布式感知系统的数据处理方法及系统。

背景技术：
随着集成电路、无线通信等各领域技术的不断进步，无线分布式感知系统已经广泛应用于工农业控制、生物医疗、环境质量监测、抢险救灾以及国防军事等领域。在无线分布式感知系统中，各分布式节点分别采集到局部数据之后，将数据通过无线链路直接或间接传递给汇聚节点，然后通过汇聚节点的融合处理得到全貌信息。所以感知数据的传输与处理策略是无线分布式感知系统的支撑技术，其有效性与可靠性直接决定了各种无线分布式感知系统的价值与应用前景。在已有的研究中，感知数据的传输与处理策略可大致分为两类：（1）基于特定路由的多跳存储转发策略。这种策略是最传统的信息传输策略，它的优点是设计简单，而且汇聚节点对全貌信息的感知是一个渐进过程。但存在的问题是数据传输效率不高，且对抗链路中断或节点失效等干扰因素的能力差。（2）基于网络编码的数据传输与处理策略。2000年，RudolfAhlswede等人在《NetworkInformationFlow》论文里提出了网络编码的概念，指出对组播网络中的某些节点附加额外的编码操作能使源点与组播成员间达到最大流最小割的组播速率，证明了组播网络中利用线性编码达到最大信息流量的可能性。同年，在论文《Linearnetworkcoding》中，Li等人提出了线性编码的方法，将数据块看作是某个基上的向量并在节点中将其进行线性变换，之后再发送出去。它指出了对于有向的组播网络只需采用线性网络编码即可达到最大组播速率。2004年，在论文《Decentralizednetworkcoding》中，CFragouli等人首次针对组播网络提出了确定系数的分布式网络编码算法，其核心思想是将网络拓扑结构分割成若干个子树，并保证每个子树的编码向量属于其父树编码向量的扩张空间，且任意两个子树的共有信宿的编码向量均线性无关。该方法具有良好的可扩展性，但是只是一个次优的算法，因为该算法所需的字母表空间随节点规模呈线性增长。2006年，TraceyHo等人在论文《ARandomLinearNetworkCodingApproachtoMulticast》中，给出了一种随机系数的分布式网络编码算法，其编码系数从有限域中均匀随机选取。该方法对线性相关的信源具有信息压缩作用，适用于链路动态变化的场景，当给定的字母表足够大时能渐进达到最大组播速率，具有很强的实用性。而具体到分布式无线传感器网络，针对没有汇聚节点，每个节点自贮存信息直到被收集节点采集走的场景，在论文《Decentralizederasurecodesfordistributednetworkedstorage》与《Datapersistenceinlarge-scalesensornetworkswithdecentralizedfountaincodes》中分别提出分布式擦除码和分布式喷泉码两种纠删码，能够有效减少传输和计算能耗并降低解码复杂性。但是遗憾在于它们并没有发掘出无线传感器网络中信号的可压缩性。综上所述，相对于第一种传输策略，网络编码的引入大大提升感知数据的传输效率，且对抗链路中断或节点失效等不稳定因素的能力较佳。但这种策略仍然存在两个较大缺陷：一是没有利用感知数据的内在相关性，无法对感知数据实现分布式压缩，致使对传输有效性的挖掘不够；二是汇聚节点的解码存在“全有或全无”（All-or-Nothing）问题。

技术实现要素：
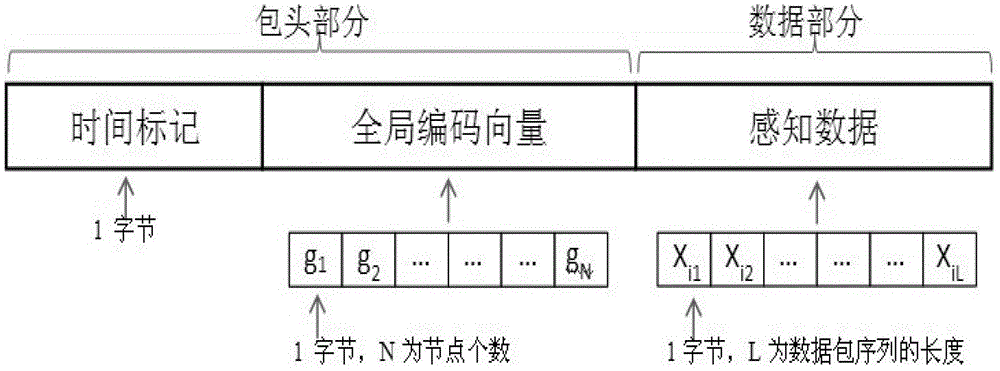
为了解决现有技术中的问题，本发明提供了一种适合无线分布式感知系统的数据处理方法。本发明提供了一种适合无线分布式感知系统的数据处理方法，包括如下步骤：A.传感器节点采集具有相关性的感知数据；B.中间节点利用随机线性网络编码对感知数据进行处理；C.传感器节点为N个，汇聚节点为m个，设源数据为x，汇聚节点接收的数据为y，汇聚节点把接收到的输入向量进行组合，得到线性方程组y=Φx，由于m<N,方程组是欠定的，故将解欠定方程组的问题转化为l1最小化问题，从而重构原始感知数据；D.接收端接收原始感知数据；、l1最小化问题：如果原始信号x是稀疏的或者是可压缩的，那么x的恢复问题可以看作为如下形式的优化问题：s.t.y=Φx。作为本发明的进一步改进，在所述步骤C中，利用压缩感知理论，解决l1最小化问题，对原始感知数据进行重构。作为本发明的进一步改进，在所述步骤C中，通过贪婪算法解决l1最小化问题，利用有限的测量值对原始感知数据进行重构。作为本发明的进一步改进，所述贪婪算法采用正交匹配追踪算法。作为本发明的进一步改进，在所述步骤A中，传感器节点采集具有相关性的感知数据形成数据包，并将该数据包传输给中间节点；所述数据包由包头部分和数据部分组成，所述包头部分由时间标记和全局编码向量构成，所述数据部分为感知数据；同一时隙被采集到的数据包被认为是同一代的包，时间标记是一个整数，时间标记代表着该数据包属于第几代；全局编码向量由N个单精度浮点数表示，其中N值等于传感器节点个数；然后从集合{1,2,…N}中为每个节点分配ID，如果某个数据包由ID为i的源点发出，全局编码向量将会被初始化为单位向量，其中只有第i个元素值为1，其余元素均为0。本发明还提供了一种适合无线分布式感知系统的数据处理系统，包括：采集单元，用于传感器节点采集具有相关性的感知数据；处理单元，用于中间节点利用随机线性网络编码对感知数据进行处理；转化及重构单元，用于将解欠定方程组的问题转化为l1最小化问题，传感器节点为N个，汇聚节点为m个，设源数据为x，汇聚节点接收的数据为y，汇聚节点把接收到的输入向量进行组合，得到线性方程组y=Φx，由于m<N,方程组是欠定的，从而重构原始感知数据；接收单元，用于接收端接收原始感知数据。作为本发明的进一步改进，在所述转化及重构单元中，利用压缩感知理论，解决l1最小化问题，对原始感知数据进行重构。作为本发明的进一步改进，在所述转化及重构单元中，通过贪婪算法解决l1最小化问题，利用有限的测量值对原始感知数据进行重构。作为本发明的进一步改进，所述贪婪算法采用正交匹配追踪算法。作为本发明的进一步改进，在所述采集单元中，传感器节点采集具有相关性的感知数据形成数据包，并将该数据包传输给中间节点；所述数据包由包头部分和数据部分组成，所述包头部分由时间标记和全局编码向量构成，所述数据部分为感知数据；同一时隙被采集到的数据包被认为是同一代的包，时间标记是一个整数，时间标记代表着该数据包属于第几代；全局编码向量由N个单精度浮点数表示，其中N值等于传感器节点个数；然后从集合{1,2,…N}中为每个节点分配ID，如果某个数据包由ID为i的源点发出，全局编码向量将会被初始化为单位向量，其中只有第i个元素值为1，其余元素均为0。本发明的有益效果是：由于本发明在汇聚节点解码阶段引入了压缩感知理论，有效解决了“全有或全无”问题。根据压缩感知理论，源数据的重构只需要少量编码数据包，且随着接收到的编码数据包数量的逐渐增多，重构性能越来越好，汇聚节点对全貌数据的感知是渐进型的，避免了“全有或全无”问题。附图说明图1是本发明的中间节点随机网络编码的示意图。图2是本发明的数据包格式示意图。图3是本发明的源数据包发出时GCV初始化示意图。图4是本发明的方法流程图。图5是本发明的原理框图。图6是鄂霍次克海中的传感器节点的大致分布示意图。图7是节点采集数据的温度图。图8是随机节点顺序下，温度值读数与经过离散余弦变换后的形式。图9是调整节点顺序后，温度值读数与经过离散余弦变换后的形式。图10是任意有序数据在离散余弦变换上展开后的系数值。图11是不同大小的G的情况GΨ满足RIP的概率图。图12是传统网络编码方案与压缩网络编码方案分别在每一代中汇聚节点收到的G的秩的值。图13是传统网络编码方案与压缩网络编码方案在重构出的数据包个数与数据采集效率上的对比图。具体实施方式如图4所示，本发明公开了一种适合无线分布式感知系统的数据处理方法，包括如下步骤：在步骤S1中，传感器节点采集具有相关性的感知数据；在步骤S2中，中间节点利用随机线性网络编码对感知数据进行处理；在步骤S3中，传感器节点为N个，汇聚节点为m个，设源数据为x，汇聚节点接收的数据为y，汇聚节点把接收到的输入向量进行组合，得到线性方程组y=Φx，由于m<N,方程组是欠定的，故将解欠定方程组的问题转化为l1最小化问题，从而重构原始感知数据；在步骤S4中，接收端接收原始感知数据。l1最小化问题：如果原始信号x是稀疏的或者是可压缩的，那么x的恢复问题可以看作为如下形式的优化问题：s.t.y=Φx。由于目标函数是零范数的，而零范数是非凸的，所以很难求解。我们可以用一范数代替零范数，将非凸的问题转化为凸问题的求解。而且已经证明，一范数的最小化即l1最小化亦能使问题得到解决。在所述步骤S3中，利用压缩感知理论，解决l1最小化问题，对原始感知数据进行重构。作为本发明的优选实施例，在所述步骤S3中，通过贪婪算法解决l1最小化问题，利用有限的测量值对原始感知数据进行重构。所述贪婪算法采用正交匹配追踪算法。在所述步骤S1中，传感器节点采集具有相关性的感知数据形成数据包，并将该数据包传输给中间节点；所述数据包由包头部分和数据部分组成，所述包头部分由时间标记和全局编码向量构成，所述数据部分为感知数据；同一时隙被采集到的数据包被认为是同一代的包，时间标记是一个整数，时间标记代表着该数据包属于第几代；全局编码向量由N个单精度浮点数表示，其中N值等于传感器节点个数；然后从集合{1,2,…N}中为每个节点分配ID，如果某个数据包由ID为i的源点发出，全局编码向量将会被初始化为单位向量，其中只有第i个元素值为1，其余元素均为0。本发明还公开了一种适合无线分布式感知系统的数据处理系统，包括：采集单元，用于传感器节点采集具有相关性的感知数据；处理单元，用于中间节点利用随机线性网络编码对感知数据进行处理；转化及重构单元，用于将解欠定方程组的问题转化为l1最小化问题，传感器节点为N个，汇聚节点为m个，设源数据为x，汇聚节点接收的数据为y，汇聚节点把接收到的输入向量进行组合，得到线性方程组y=Φx，由于m<N,方程组是欠定的，从而重构原始感知数据；接收单元，用于接收端接收原始感知数据。在所述转化及重构单元中，利用压缩感知理论，解决l1最小化问题，对原始感知数据进行重构。在所述转化及重构单元中，通过贪婪算法解决l1最小化问题，利用有限的测量值对原始感知数据进行重构。所述贪婪算法采用正交匹配追踪算法。在所述采集单元中，传感器节点采集具有相关性的感知数据形成数据包，并将该数据包传输给中间节点；所述数据包由包头部分和数据部分组成，所述包头部分由时间标记和全局编码向量构成，所述数据部分为感知数据；同一时隙被采集到的数据包被认为是同一代的包，时间标记是一个整数，时间标记代表着该数据包属于第几代；全局编码向量由N个单精度浮点数表示，其中N值等于传感器节点个数；然后从集合{1,2,…N}中为每个节点分配ID，如果某个数据包由ID为i的源点发出，全局编码向量将会被初始化为单位向量，其中只有第i个元素值为1，其余元素均为0。本发明要解决的技术问题首先是网络编码策略中汇聚节点解码的“全有或全无”（All-or-Nothing）问题：即如果信源发出N个原始数据包，为了重构原始数据，目的节点必须收到至少N个线性独立的数据包。如果收到的数据少于N个，那么几乎无法重构任何原始数据。该问题会导致严重的丢包问题，从而影响整个网络的吞吐量，极大地限制了无线分布式感知系统的应用空间。此外，现有技术对无线分布式感知系统的另一特性挖掘利用不足：感知数据往往存在内在相关性。这种内在相关性决定了可以对分布式感知数据实施压缩以进一步提高传输效率、节省能源。本发明就是利用随机线性网络编码与压缩感知之间的天然契合性（由于随机线性网络编码方案中的编码操作与压缩感知中的随机投影操作是相似的），提出以网络编码为手段来实现对分布式感知数据的压缩测量与重构。从而解决了“全有或全无”与分布式压缩问题，并保留了网络编码策略原有的优点。在步骤S2中（技术特征1），节点将接收到的数据包利用通过随机方法选择的系数进行随机线性组合，再将它传输出去。参照图1，假设源与接收端均为2个的情况下，其中x1与x2为源数据，ξi是从有限域中随机选取的系数，每条边上箭头标示的是在该条边上传输的处理结果。我们假设源的个数为N，接收端的个数为m，源数据包的长度为L，向量表示形式为xi=[xi1,xi2,…xiL]，那么网络中任意一条边e上传输的序列y(e)则可以表示为线性组合的形式y(e)=g(e)·[x1T,x2T…xNT]T。其中向量g(e)=[g1,g2…gN]即为边e上的全局编码向量（GCV）。矩阵形式见下式：在一个或多个时步之后，根据传统网络编码方案，只要矩阵G的秩为N，那么源数据都可以由任意汇聚节点在同一时间点由输入边接收到的符号序列重构出来。中间节点利用随机线性网络编码对感知数据进行处理的步骤如下：1.如图1所示，两个源X1与X2发送数据；2.到达下一个节点后，将X1与X2乘以随机系数后相加，即将X1与X2进行随机线性组合后整合为一个数据再次发送出去；3.到达下一级节点后，将上一级整合后的数据作为接收到的数据再次进行随机线性组合，即重复2的过程，之后再将再次组合的一个数据发送出去；4.重复以上步骤，直至发送到汇聚节点为止。本发明的数据包格式（技术特征2）：参照图2，它不需要任何集中式的图形结构或是集中式的编码、解码函数。包头区域由两个部分组成：时间标记与全局编码向量。在实际的网络中，不同节点并不会同时接收或传输数据包，而是可能按顺序接收包含不可合并部分的多个数据包。不同路径上有重叠部分的数据包也通常会受限于损耗、障碍、多径时延或是其他由于路径冲突带来的变化。在本技术（发明）中，所有含可合并数据的包（也就是同一时隙被采集到的数据包）被认为是同一代的包。时间标记是一个整数，代表着该数据包属于第几代。全局编码向量由N个单精度浮点数表示，其中N值等于该无线传感器网络中的节点个数。然后从集合{1,2,…N}中为每个节点分配ID。参照图3，如果某个数据包由ID为i的源点发出，全局编码向量将会被初始化为单位向量，其中只有第i个元素值为1，其余元素均为0,。根据所述理论，如果收到的包的全局编码向量中有非零元素，那么ID与非零元素相对应的源点的信息就包含在这个包中。步骤S3中（技术特征3），WSN中的任意信号都可以看成是一个实值、有限、一维、离散的向量，实域中大小为N×1的列向量可表示为x=[x1,x2,…,xN]T。实域中的任意信号x可以按照标准正交基展开，由N×1的向量ψj表示，ψj=[ψj1,ψj2,…,ψjN]T,j=1,2,…,N。利用ψj作为列向量的N×N的基矩阵Ψ=[ψ1|ψ2|…|ψN]，信号x的表达式见下式：orx=Ψs，式中s=[s1,s2,…,sN]T。由上述可知，信号既能用x表示，也能用s表示。x是在时间或空间域上，s则是在Ψ域上。如果信号x是由K个基向量线性组合而成，那么x就是K项稀疏的。也就是说，在上式中的系数si仅有K个是非零的。一个特殊情况是当K＜＜N时，只有s中值较大的系数占很少的比例时，信号x才是可压缩的。我们考虑一个欠定的方程组y=Φx，其中Φ是大小为m×N的随机投影矩阵（m<N），x是K项稀疏的或是在Ψ域上可压缩的。那么该方程组可改写成y=Φx=ΦΨs。根据压缩感知中的结论，如果积矩阵ΦΨ满足RIP性质——对所有s，||s||0≤K，则存在一个δ2k∈(0,1)，使得——那么x能否有效重构的问题就转化为一个l1最小化问题：s.t.y=Φx,x=Ψs。再考虑到技术特征1提到的随机线性网络编码系统，全局编码向量矩阵G是随机生成的，并且[x1jx2j…xNj]T是可压缩的。在构造一个合适的G并找到感知数据的稀疏特性的条件下，甚至当G非满秩时，我们也能够通过解决l1最小化问题来重构源数据。在步骤S3中（技术特征4），l1最小化已证明可以用于精确重构，并且存在一个高效、精确的处理方式解决上文提及的凸优化问题。贪婪算法依靠的是对信号稀疏系数和支撑集的迭代估计，一种方式是在到达收敛规则前对信号的支撑集进行迭代识别，还有一种是在每次试图解释测量值失配的迭代中得到稀疏信号的改进估计。正交匹配追踪算法（OMP）是最为简单和普遍的贪婪算法之一，它在积矩阵ΦΨ中找到与测量值相关性最强的一列，然后将各列与信号的残差相关，再重复这一步。这里的残差，即是从原始测量向量中减去部分估计信号的贡献得到的。如果测量矩阵满足RIP性质，对于K项稀疏的信号x与无噪声的测量值y，OMP至少能保证在K次迭代之后精确还原出x。在技术特征4中，通过通过贪婪算法解决l1最小化问题的方法：（算法1（正交匹配追踪算法）输入：CS测量值y，测量矩阵Θ=ΦΨ={θi,i=1,2,...,N}，其中Φ∈R，Ψ∈R。初始化：索引残差r=y，稀疏表达式s=0∈RN。迭代：输出：稀疏表达式s，与源数据x=Ψs本地编码向量（LCV）的选择（技术特征5）：根据2005年Jaggi等人在论文《PolynomialTimeAlgorithmsforMulticastNetworkCodeConstruction》中提到的，如果本地编码向量是随机生成的并处于一个足够大的有限域中，那么如同信号一样，任意汇聚节点收到的全局编码矩阵G都是高概率满秩的。但是，在一个有限域中，保证感知信号可以被稀疏表示并且GΨ满足压缩感知理论的RIP性质的前提下，找到一个合适的基Ψ是比较困难的。这里选择Rademacher分布在实域上的随机变量来构造本地编码向量，见下式：式中mi(e)为边e的LCV的第i个元素的值。我们知道，在多次的乘法操作之后，汇聚节点收到的全局编码矩阵G将变成正态分布。在合适的场景下，例如海洋气候传感器网络中，空间相关的测量值在经过适当组合与离散余弦变换后是可压缩的。本技术（发明）的实施方式中的论证证明了，在上述场景下，GΨ（正态分布随机矩阵与离散余弦变换）有十分好的RIP特性。本技术（发明）与传统方法相比具有如下优点：1、由于本发明在中间节点编码阶段利用了网络编码技术，有效提升了无线传感器网络中的感知数据的传输效率。由技术特征1带来的，中间节点利用的随机线性网络编码虽然简单，但却是一个强大的编码方案。在广播传输方案中，它利用非集中式的算法可以将网络吞吐量达到最佳值。在传统的WSN场景下，集中式的网络管理和控制十分复杂，随机线性网络编码能够有效地使每个节点以非集中的方式工作并达到最优性能。因此，不必需要知道所有的网络配置，就可以使网络节点分布式工作。2、由于本发明给出了可行的改进的数据包格式，有效利用了无线传感器网络中信号的相关性。由技术特征2带来的，在有益效果1的基础上进一步改善了数据传输的有效性。3、由于本发明在汇聚节点解码阶段引入了压缩感知理论，有效解决了“全有或全无”问题。由技术特征3、4带来的，根据压缩感知理论，源数据的重构只需要少量编码数据包，且随着接收到的编码数据包数量的逐渐增多，重构性能越来越好，汇聚节点对全貌数据的感知是渐进型的，避免了“全有或全无”问题。技术特征5则是保证该有益效果可行的理论基础。参照图4，本发明首先需要采集有相关性的感知数据。我们利用美国国家海洋数据中心的数据进行数值实验，数据来自分布在鄂霍次克海中的传感器测量值，图6描述了传感器节点的大致分布，每个传感器节点采集到的数据如图7所示。参照图5，为了评估感知数据的相关性与压缩性能，选择同一时间鄂霍次克海中分布节点的感知的一系列温度数据。首先按照随机顺序从节点中读取数据，图8中显示的是它们的读数与经过离散余弦变换后的形式。可以发现相对较大的系数占绝大多数。然后，经过若干次测试，再选择一个更加合适的节点排列并将节点按照此顺序编号。之后按顺序收集所有节点的数据，在某时间点它们的读数与离散余弦变换后的表达式如图9所示。最后，按照上述顺序读取数据，我们测试了2012年鄂霍次克海的所有温度数据，如图10所示，任意有序数据在离散余弦变换上的展开式只有13至16个系数不接近0。然后考虑由GCV矩阵和DCT矩阵组成的测量矩阵（GΨ）的RIP性质。在本发明中，待处理信号x的长度为N=118，它在离散余弦变换上的线性组合有K=13～16个系数不接近零，所以汇聚节点随机接收的GCV矩阵的大小为m×118,m=30,45,60,75。根据公式我们研究不同m下的δ。图11表明了当汇聚节点收到的G的秩达到75时，测量矩阵会以高概率满足RIP性质，即信号x能够以高概率精确重构。为了简单而不失普遍性，我们在118个节点中会随机选取一个作为汇聚节点。每次试验发送500代数据包，图12显示的是每一代中汇聚节点收到的GCV矩阵的秩。在利用有限域元素作为本地编码向量的传统网络编码方案中，汇聚节点以83.5的概率收到满秩的GCV矩阵。而在利用Rademacher分布随机系数作为本地编码向量的压缩网络编码方案中，每一代汇聚节点收到GCV矩阵几乎都是非满秩，但是所有秩的值都大于75，大致在85-110范围内。图13A展示的是两种方案以代为自变量精确重构出的数据包个数。经过对两种方案数据采集效率比率的计算发现，本技术（发明）的效率比传统网络编码方案高出20%～35%，比较结果如图13B所示。WSN即WirelessSensorNetwork的缩写，中文含义为无线传感器网络。压缩感知:WSN中的任意信号都可以看成是一个实值、有限、一维、离散的向量，实域中大小为N×1的列向量可表示为x=[x1,x2,…,xN]T。实域中的任意信号x可以按照标准正交基展开，由N×1的向量ψj表示，ψj=[ψj1,ψj2,…,ψjN]T,j=1,2,…,N。利用ψj作为列向量的N×N的基矩阵Ψ=[ψ1|ψ2|…|ψN]，信号x的表达式见下式：orx=Ψs（2）其中s=[s1,s2,…,sN]T。由上述可知，信号既能用x表示，也能用s表示。x是在时间或空间域上，s则是在Ψ域上。如果信号x是由K个基向量线性组合而成，那么x就是K项稀疏的。也就是说，在式（2）中的系数si仅有K个是非零的。一个特殊情况是当K＜＜N时，只有s中值较大的系数占很少的比例时，信号x才是可压缩的。考虑一个欠定的方程组：y=Φx（3）其中Φ是大小为m×N的随机投影矩阵（m<N），x是K项稀疏的或是在Ψ域上可压缩的。那么该方程组可改写成：y=Φx=ΦΨs（4）根据压缩感知中的结论，如果积矩阵Θ=ΦΨ满足RIP性质：对任意K=1,2,…，定义矩阵Θ的等距常量δK为满足下式的最小值，其中s满足||s||0≤K：如果δK<1，称矩阵Θ满足K阶RIP；那么x能否有效重构的问题就转化为一个l1最小化问题：s.t.y=Φx,x=Ψs（6）由随机线性网络编码可知，全局编码向量矩阵G是随机生成的，并且向量[β1jβ2j…βNj]T是可压缩的。在生成一个合适的G并且感知数据满足稀疏特性的条件下，甚至当G非满秩时，我们也能够通过解决l1最小化问题来重构源数据。压缩采样信号的重建问题存在多种求解方案，包括基追踪（BasisPursuit,BP）、贪婪算法等。基追踪具有较好的重建性能，但是运算量较大。贪婪算法将重建问题看作过完备字典的信号稀疏分解问题求解，其经典算法如匹配追踪算法、正交匹配追踪（OrthogonalMatchingPursuit,OMP）算法等。正交匹配追踪算法（OMP）是最为简单和普遍的贪婪算法之一，它在ΦΨ中找到与测量值相关性最强的一列，然后将各列与信号的残差相关，再重复这一步[18]。这里的残差，即是从原始测量向量中减去部分估计信号的贡献得到的。如果测量矩阵满足RIP性质，对于K项稀疏的信号x与无噪声的测量值y，OMP至少能保证在K次迭代之后精确还原出x。该算法正式的定义如下：算法1（正交匹配追踪算法）输入：CS测量值y，测量矩阵Θ=ΦΨ={θi,i=1,2,...,N}，其中Φ∈R，Ψ∈R。初始化：索引残差r=y，稀疏表达式s=0∈RN。迭代：输出：稀疏表达式s，与源数据x=Ψs。以上内容是结合具体的优选实施方式对本发明所作的进一步详细说明，不能认定本发明的具体实施只局限于这些说明。对于本发明所属技术领域的普通技术人员来说，在不脱离本发明构思的前提下，还可以做出若干简单推演或替换，都应当视为属于本发明的保护范围。