基于图形处理器的条带波变换图像压缩方法与流程

本发明属于图像处理技术领域，更进一步涉及图像压缩技术领域中的一种基于图形处理器的条带波变换图像压缩方法。可用于医学图像处理、网络图像传输、移动多媒体等领域。

背景技术：
图像压缩的目的是使用尽可能少的数据量对图像进行表示。图像压缩技术在医学图像处理、高清晰度电视、卫星遥感等领域均有着广泛的应用前景。图样本身包含大量的信息，但图像本身含有大量的冗余信息，例如：图像中相邻像素间的相关性引起的空间冗余、编码冗余、图像中非常强的纹理结构而引起的结构冗余等，图像压缩就是去掉图像的冗余信息，但如何有效地去除图像的冗余信息仍需要提出新的研究方法，而且压缩图像需要很高的压缩比和较快的计算速度。中央处理器（CPU)的设计目标是使执行单元能够以很低的延迟获得数据和指令,因此,中央处理器具有复杂的控制逻辑和很强的分支预测能力,并使用大量的缓存来提高效率，由于功耗和设计难度的限制，CPU性能的提高遇到了瓶颈,多核成为处理器设计发展的方向，而采用众核架构的图形处理器（GPU）很适合执行需要大运算量、具有数据独立性质的科学运算，图形处理器很适合来加速图像处理算法。条带波变换（Bandelet变换）是和小波变换类似的对图像进行表示的方法，Bandelet变换的基本思想是对特定尺度上的高频小波系数沿图像几何流方向再进行一维小波变换，以此获得更少的非零系数和去除奇异点附近的小波系数间的相关性，故条带波变换拥有比小波变换更好的图像表示能力。目前已经有各种图像压缩技术被提出，例如目前使用很广泛的基于JPEG的图像压缩标准，JPEG图像压缩标准基于离散余弦变换，该方法有易于实现、用可变的压缩比控制文件大小的优点，但是在较高的压缩比下，重构图像存在严重的块效应，不能很好地适应网络传输图像的需要，而且不具有很多所需要的特性，例如：质量渐进、良好的低比特率压缩性能等。江苏新瑞峰信息科技有限公司申请的专利“一种快速JPEG2000图像压缩系统”（专利申请号：CN201310375029，公开号：CN103414901A）中构建了以JPEG2000算法为基础的图像压缩系统，该系统以离散小波变换技术为基础，并使用了图形处理器来加速算法，小波变换虽然可以很好的对规则图形进行压缩，且只有奇异点附近的小波系数是非零的，但是该系统仍然存在的不足是：小波只能扑捉点状的奇异点，不能很好的处理线状和面状的奇异点。中国矿业大学申请的专利“一种改进条带波变换的图像压缩方法”（专利申请号：CN201310484868，公开号：CN103561275A）中公开了一种改进条带波变换的图像压缩方法。该方法首先将图像进行条带波变换，然后使用嵌入式零树小波编码对条带波系数进编码以及解码，最后实现图像压缩的效果，该方法具有图像压缩比和峰值信噪比高的特点，但是仍然存在的不足是：条带波变换过程比较复杂，而且计算量很大。

技术实现要素：
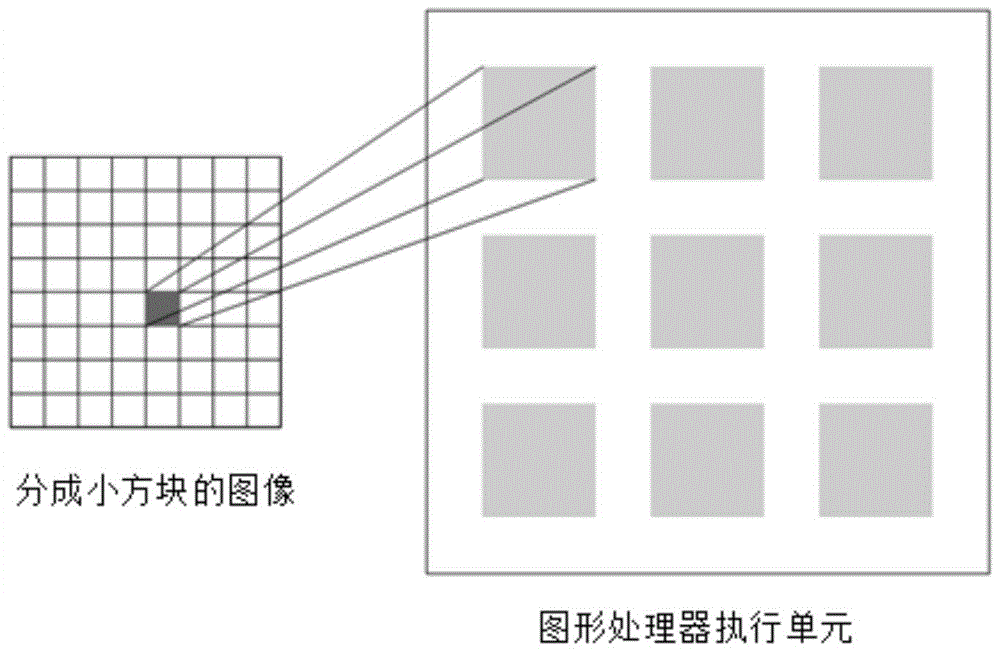
本发明的目的是针对上述现有技术的不足，提出了一种基于图形处理器的条带波变换图像压缩方法，并采用具有众核架构图形处理器来加速算法。解决了算法速度慢的问题，并提高了压缩图像的峰值信噪比，并且解压过程很容易实现。本发明实现的具体步骤包括如下：（1）输入待压缩图像：输入待压缩图像，从输入的待压缩图像中读取数值矩阵，将数值矩阵从内存传输到显存中。（2)小波变换：对数值矩阵进行二维哈尔小波变换，得到哈尔小波系数矩阵。（3）Bandelet化：（3a）将哈尔小波系数矩阵分解成边长为8的小方块,将小方块内的系数加载到图形处理器的共享存储器中，对于每个小方块，在（0，π)区间内，等间隔地抽取32个角度值作为几何流的方向，用符号INF表示无几何流方向；（3b)采用投影值公式，计算每个小方块内哈尔小波系数的坐标在抽取的32个几何流方向上的正交投影值；（3c）将正交投影值按从小到大排序，得到一个长为64的排序索引,对于无几何流方向，排序索引为数字1～64；（3d）将小方块内的哈尔小波系数，按照排序索引进行重新排序，得到一个一维信号，对一维信号进行一维哈尔小波变换，得到小波变换后的一维信号，对小波变换后的一维信号进行量化处理，得到量化后的一维信号，对量化后的一维信号进行一维哈尔小波逆变换得到重构信号；（3e）计算估计误差，选择使估计误差最小的方向作为小方块的最佳几何流方向；（3f）采用投影值公式，计算每个小方块内哈尔小波系数的坐标在最佳几何流方向上的正交投影值，将正交投影值按从小到大排序，得到一个长为64的排序索引，若最佳几何流方向是无几何流方向，排序索引为数字1～64,，使用排序索引重新排序小方块内的哈尔小波系数，得到一维信号，对一维信号，进行一维哈尔小波变换，得到哈尔小波变换后的一维信号，使用排序索引，对哈尔小波变换后的一维信号进行重新排序，得到Bandelet变换系数矩阵；（3g）将Bandelet变换系数矩阵转换为整型值；（3h）将Bandelet变换系数矩阵从显存传回内存。（4）嵌入式零树小波编码：（4a）采用嵌入式零树小波方法，对Bandelet变换系数矩阵进行扫描，得到扫描符号列表；（4b）对扫描符号列表进行霍夫曼编码，得到二进制码流，根据图像的像素深度来控制压缩文件的大小；（4c）使用数字对几何流方向进行编码，用数字0～31分别表示等间隔地抽取出来的32个方向值，用数字32表示无几何流方向的符号INF，将二进制码流、嵌入式零树小波扫描的初始阈值、每轮主扫描表和辅扫描表的长度、哈尔小波变换的迭代次数、压缩图像的尺寸、霍夫曼码表、每个小方块内的最佳几何流的方向写入压缩文件中；（4d）输出压缩文件。（5）输入待解压的压缩文件：输入待解压的压缩文件,从压缩文件中提取霍夫曼码表。（6）解码：（6a）从压缩文件中读取二进制码流，对二进制码流进行霍夫曼解码，得到嵌入式零树小波的扫描符号列表；（6b）对扫描符号列表进行嵌入式零树小波解码，得到Bandelet变换的系数矩阵。（7）Bandelet逆变换：（7a)将得到的Bandelet系数矩阵从内存传输到显存中；（7b）将Bandelet系数矩阵分成边长为8的小方块，将小方块内的Bandelet系数从显存读取到图形处理器的共享存储器中；（7c）从压缩文件中读取每个小方块内的最佳几何流的方向，采用投影值公式，计算每个小方块内Bandelet系数的坐标在最佳几何流方向上的正交投影值，将正交投影值按从小到大排序，得到一个长为64的排序索引，若最佳几何流方向是无几何流方向，排序索引为数字1～64，采用排序索引重新排序小方块内的Bandelet变换系数，得到一个一维信号，对一维信号进行一维哈尔小波逆变换得到哈尔小波逆变换后的一维信号，采用排序索引重新排序哈尔小波逆变换后的一维信号，得到哈尔小波变换矩阵；（7d）对哈尔小波变换矩阵进行二维哈尔小波逆变换，得到压缩图像的重构图像；（7e）将压缩图像的重构图像从显存传回内存。本发明与现有技术相比具有以下优点：第一、由于本发明采用能很好地对图像进行表示的Bandelet变换的方法，克服了现有技术中对图像表示不好的问题，使得本发明的重构图像的细节特征能够得到很好的保留。第二、由于本发明采用图像处理器来进行Bandelet变换，图像处理器具有众核架构，很适合执行需要大运算量、具有数据独立性质的并行计算，克服了现有技术中对图像进行压缩处理速度慢的问题，使得本发明对图像进行压缩处理的速度加快。第三、由于本发明采用嵌入式零树小波的方法，嵌入式零树小波能很好地压缩Bandelet变换后的系数，克服了现有技术中压缩比低的问题，使得本发明的压缩比很高，提升了压缩图像的峰值信噪比。附图说明图1是本发明的流程图；图2是本发明的Bandelet变换在GPU上读取数据的示意图；图3是本发明仿真使用的测试图；图4是本发明与现有技术哈尔小波的压缩效果图。具体实施方式下面结合附图对本发明做进一步的描述。参照图1，本发明实现的具体步骤如下：步骤1，输入待压缩图像。输入待压缩图像，从输入的待压缩图像中读取数值矩阵，将数值矩阵从内存传输到显存中。步骤2，小波变换。小波变换步骤如下：第一步，按照下式，计算哈尔小波变换的迭代次数，N＝log2(W)-3其中，N表示哈尔小波变换的迭代次数，W表示待压缩图像的宽度；第二步，图形处理器对数值矩阵的每一行元素进行一维哈尔小波变换；第三步，对数值矩阵的每一列元素进行一维哈尔小波变换；第四步，重复第二步、第三步，直至达到迭代次数N，得到哈尔小波系数矩阵。步骤3，Bandelet化。对所获得的二维小波系数矩阵进行Bandelet化得到Bandelet变换系数。为了更高效地使用GPU的特性，将二维小波系数矩阵分成块状，本发明将小波系数矩阵分成边长为8×8的小方块，好处是Bandelet正变换和逆变换都很容易实现，而且可以发挥GPU的优点。共享存储器属于片上存储器，读写速度远快于显存，如图2,Bandelet变换在GPU上读取数据的示意图所示,将小方块内的系数读取到图形处理器的共享存储器中，在GPU执行Bandelet化的过程中，每个线程块执行边长为8×8的小方块的Bandelet化，由于8×8小方块内的像素个数为64，一个线程处理一个像素，线程块中包含的线程数量为64个，而线程块的数量为图像的宽度的平方除以64。执行Bandelet化时需要搜索最佳几何流方向，将哈尔小波系数矩阵分解成边长为8的多个小方块,对于每个小方块，在（0，π)区间内，等间隔地抽取32个角度值作为几何流的方向，用符号INF表示无几何流方向，表示不实施Bandelet化。采用投影值计算公式，计算每个小方块内哈尔小波系数的坐标在抽取32个几何流方向上的正交投影值,投影值公式如下：-sin(θ)*x+cos(θ)*y其中，θ表示几何流方向，x,y分别表示小方块系数的坐标。将正交投影值按从小到大排序，得到一个长为64的排序索引，对于无几何流方向，排序索引为数字1～64。将小方块内的哈尔小波系数，按照排序索引进行重新排序，得到一个一维信号，对一维信号进行一维哈尔小波变换，得到小波变换后的一维信号，采用下式，对小波变换后的一维信号进行量化处理，得到量化后的一维信号，对量化后的一维信号进行一维哈尔小波逆变换得到重构信号，T]]>其中，Q(x)表示量化后的一维信号，x表示小波变换后的一维信号的元素，T表示阈值，q表示满足q*T≤|x|≤(q+1)*T条件的整数，sign表示取元素符号的操作；使用下式计算估计误差，选择使估计误差最小的方向作为小方块的最佳几何流方向,E＝||f1-f4||2+λT2(R1+R2)其中，E表示估计误差，f1表示重新排序的一维信号，f4表示对量化的信号执行一维哈尔小波逆变换得到的重构信号，λ等于T表示阈值，R1表示编码几何流方向所需的比特位，R2表示编码量化系数所需的比特位。使用小方块内的最佳几何流方向和投影值计算公式，计算每个小方块内哈尔小波系数的坐标在几何流方向上的正交投影值，将正交投影值按从小到大排序，得到一个长为64的排序索引，对于无几何流方向，排序索引为数字1～64，使用排序索引来重新排序小方块内的哈尔小波系数，得到一维信号，对一维信号，进行一维哈尔小波变换，得到哈尔小波变换后的一维信号，使用排序索引对哈尔小波变换后的一维信号进行重新排序，得到Bandelet变换系数矩阵。将Bandelet变换系数矩阵转换为整型值。将Bandelet系数矩阵从显存传回内存。步骤4，采用嵌入式零树小波(embeddedzerotreewavelet，EZW)算法扫描Bandelet变换系数矩阵产生扫描符号。对扫描符号列表进行霍夫曼编码，得到二进制码流，根据图像的像素深度（bpp）来控制压缩文件的大小，使用数字对几何流方向进行编码，用数字0～31分别表示等间隔地抽取出来的32个方向值，用数字32表示无几何流方向的符号INF，这样可以节省对最佳几何流方向编码所需要的比特位。将二进制码流、嵌入式零树小波扫描的初始阈值、每轮主扫描表和辅扫描表的长度、哈尔小波变换的迭代次数、压缩图像的尺寸、霍夫曼码表、每个小方块内的最佳几何流的方向写入压缩文件中，输出压缩文件。嵌入式零树小波扫描过程如下：第一步，确定扫描的初始阈值，其中，T0表示扫描的初始阈值，F表示向下取整操作，M表示取所有系数的最大值操作，C表示Bandelet变换系数；第二步，将Bandelet变换系数与阈值进行比较，给Bandelet变换系数分配以下符号的一种：P（正的重要系数）、N（负的重要系数）、T（零树根）、Z（孤立零点），得到一个扫描表；第三步，根据扫描表，对扫描结果为P或N的Bandelet变换系数进行量化；第四步，使用下式，更新下一轮扫描阈值，将阈值与0.5进行比较，当阈值等于0.5时，结束扫描，当阈值大于0.5时，进入第二步，Ti+1＝Ti/2其中，Ti为第i轮扫描的阈值，Ti+1为第i+1轮扫描的阈值。步骤5，输入待解压的压缩文件，从压缩文件中提取霍夫曼码表。步骤6，解码压缩文件。从压缩文件中读取二进制码流，对二进制码流进行霍夫曼解码，得到嵌入式零树小波的扫描符号列表，对扫描符号列表进行嵌入式零树小波解码，得到Bandelet变换的系数矩阵。步骤7，Bandelet逆变换。将得到的Bandelet系数矩阵从内存传输到显存中。将Bandelet系数矩阵分成边长为8×8的小方块，将小方块内的Bandelet系数从显存读取到图形处理器的共享存储器中。从压缩文件中读取每个小方块内的最佳几何流的方向，采用投影值计算公式，计算每个小方块内Bandelet系数的坐标在最佳几何流方向上的正交投影值，将正交投影值按从小到大排序，得到一个长为64的排序索引，对于无几何流方向，排序索引为数字1～64，采用排序索引重新排序小方块内的Bandelet变换系数，得到一个一维信号，对一维信号进行一维哈尔小波逆变换得到哈尔小波逆变换后的一维信号，采用排序索引重新排序哈尔小波逆变换后的一维信号，得到哈尔小波变换矩阵；对哈尔小波变换矩阵进行二维哈尔小波逆变换，得到压缩图像的重构图像。将压缩图像的重构图像从显存传回内存。下面结合仿真实验对本发明的效果做进一步的描述。1、仿真实验条件：本发明仿真条件为：英特尔XeonE5645中央处理器、8GB内存,英伟达K20图形处理器,CentOS版本6.4、gcc版本4.4.7、cuda版本5.5。2、实验内容与结果分析：图3是标准测试图像barbara,图4是本发明与现有技术哈尔小波分别对标准测试图像barbara进行压缩的效果图，横坐标为压缩图像的像素深度，纵坐标为峰值信噪比,从图4可以看出，当压缩率很高时，本发明的效果比哈尔小波的方法要略差，这是由于对bandelet变换的图像进行编码时，还需要编码变换图像的几何流方向，但当bpp变大时，本发明要比哈尔小波的方法效果好，峰值信噪比得到提高。表1为对不同分辨率的图像，本发明分别在CPU和GPU上运行时间（单位：毫秒），可以看出具有众核架构的图形处理器（GPU）很适合执行需要大运算量、具有数据独立性质的科学运算，图形处理器很适合来加速图像压缩算法，Bandelet变换在GPU上运行要比在CPU上至少快27倍，而最多快39倍，可以看出本发明的压缩速度很快。图像分辨率256×256512×5121024×1024CPU60.79262.501007.38GPU2.207.1025.59加速比27.5536.9339.36表1