基于系数映射变换的多项式完全同态加密方法及系统与流程

本发明涉及的是一种信息安全领域的技术，具体是一种基于系数映射变换的多项式完全同态加密方法及系统。

背景技术：

同态加密是这样一种加密方法，即对经过同态加密的数据进行处理得到一个输出，将这一输出进行解密，其结果与用同一方法处理未加密的原始数据得到的输出结果是一样的。

1978年Rivest，Adleman and Dertouzos在On Data Banks and Privacy Homomorphisms.(Foundations of Secure Communication，pp.169‐177，Academic Press.)中首先提出了同态加密的概念，当时他们使用的术语是隐私同态(privacy homomorphism)。在这篇论文中Rivest等人同时提出了几个候选的加密算法，具有同态运算的特性。多项式加密算法就是其中之一，虽然其具有原理简单，实现容易，运算迅速等优势，但是由于极易受到明文攻击，安全性没有保障，因此无法直接使用。其他候选算法也很快发现安全隐患，同时又因为缺乏新的算法，该问题慢慢淡出了人们的视线。1991年同态加密问题再次被学术界所关注，Feigenbaum，Merritt的Open Questions，Talk Abstracts，and Summary of Discussions.(DIMACS Series in Discrete Mathematics and Theoretical Computer Science，Vol 2，pp.1‐45.)在回顾应用数学领域中几个悬而未决的问题时重新提出了对这个重要问题的思考。但是之后的研究成果依旧寥寥无几，毫无突破。

直到2009年，Craig Gentry在其博士论文A Fully Homomorphic Encryption Scheme中首度公开了一种基于理想格的同态加密算法，并正式使用了完全同态加密(Fully Homomorphic Encryption)的术语，这为之后该领域的研究奠定了基础。该方法引入随机噪声用于加密，使用类似RSA算法的大数分解难题作为其安全性的基础，并对每一步同态运算之后引入数据清洗操作，以使噪声大小始终保持在不影响计算结果的范围内。但是由于该算法十分复杂，运算过程繁复，并且针对明文的每一位(bit)进行加密，导致整体运算量十分巨大，同时其密文所需的存储空间也相当庞大，因而很难应用到实际服务中。

其后几乎所有的研究均围绕着Craig的方法进行改进和加强。针对原方法计算量大、密文存储空间大、密文扩展速度大等问题，作了大量深入的研究，也取得了不少研究成果。如Z.Brakerski，C.Gentry，and V.Vaikuntanathan.Fully Homomorphic Encryption without Bootstrapping.In ITCS 2012和Z.Brakerski and V.Vaikuntanathan.Efficient Fully Homomorphic Encryption from(Standard)LWE.In FOCS 2011(IEEE)基于原方法的框架提出了一种以误差学习难题(LWE)作为安全基础的BGV方法，减少了同态运算的计算量，使得噪音变量的增长更加缓慢，从而减少了数据清洗的操作。Lopez‐Alt，Tromer，Vaikuntanathan的On‐the‐Fly Multiparty Computation on the Cloud via Multikey Fully Homomorphic Encryption.(In STOC 2012 ACM)基于格上加密原理提出了LTV方法，也是以减少计算量，减缓噪音增长速度为优化目标。Coron，Lepoin，Tibouchi的Batch Fully Homomorphic Encryption over the Integers(EUROCRYPT 2013Springer)在原方法的基础上进行了改进，使得针对所有位的加密可以压缩到同一个密文中，这样有效的缩减了密文的大小，也一定程度上减少了计算量，但是却无法有效控制噪音，因此仍旧需要数据清洗操作。

上面所列举的研究成果，以及其他几乎所有的研究均无法完全脱离Craig原方法的思路和框架，因此，虽然新的方法比原方法有了长足的改进，实际实施该算法需要消耗的计算资源和存储资源仍然十分巨大，很难真正应用到实际服务中。这也是虽然需求明显，但是至今全世界范围尚未出现任何同态加密算法商业应用实例的原因。

技术实现要素：

本发明针对现有技术存在的上述不足，提出一种基于系数映射变换的多项式完全同态加密方法及系统，在不泄露明文的情况下直接对密文进行运算，从而提供安全的数据存储和运算环境。本发明基于改进的多项式同态加密原理，可以直接对任意整数或实数进行加密，并通过对多项式系数进行函数映射变换，将映射函数本身作为密钥的一部分，依靠求解一般形态函数方程的困难性，消除了原方法的安全性隐患。其计算速度相对于现有技术有显著提高，所要求的密文体积和扩张速度更小，更有利于各种方式的实现，使得数据所有者可以放心地使用各种云计算服务而不必再担心其敏感数据、保密数据会因此而泄露。云服务提供者也可以专心于实现客户价值和提供优质服务，而不必再担心客户会因为对数据安全的担心而不敢使用其提供的服务。

本发明是通过以下技术方案实现的：

本发明涉及一种基于系数映射变换的多项式完全同态加密方法，首先将明文表达为指定映射函数的一组随机取值、两组随机系数因子以及一个随机常数组成的多项式，并将该多项式中的：指定映射函数的表达式与一组随机系数因子作为密钥；将另一组随机系数因子、该映射函数的一组随机自变量以及随机常数作为可供同态运算的密文，通过对函数密钥部分进行三种不同的映射后经过数值拟合，分别得到三个子函数构成的运算支持函数族，用于异地进行基于运算支持函数族的密文同态运算后返回本地通过密钥进行解密。

本发明具体包括以下步骤：

步骤1、针对任意实数的明文P∈R，随机选取实数向量A＝{a_i|i∈I}以及Y＝{y_i|i∈I}，且满足：

其中：实数向量X＝{x_i|i∈I}，B∈R，I为多项式密钥维数下标集合，通常情况下I＝{1,2}；f(x_i)为函数密钥部分，优选复合函数f()为周期函数。

对应生成的密钥为K＝{f(),Y}，针对P的密文为：C＝{A,X,B}。

所述的数值拟合采用但不限于最小二乘法。

步骤2、在异地通过运算支持函数族G对密文之间或明文与密文之间进行同态运算得到密文同态运算结果C_r。

所述的同态运算包括：加、减、乘和除法及其任意组合。

步骤3、根据密文同态运算结果C_r代入密钥K中的f和Y即可解密得到明文同态运算结果P_r。

本发明涉及一种实现上述方法的系统，包括：客户端和服务端，其中：

所述的客户端用于生成密钥K以及运算支持函数族G，并对明文P进行加密或对密文C进行解密操作；

所述的服务端用于接收密文C以及运算支持函数族G，并根据运算支持函数族G对所述密文进行同态运算操作。

所述的服务端优选设有用于存储密文的数据库，进一步优选设有与密文相对应的密文ID。

所述的同态运算操作包括：密文与明文或密文的四种基本运算，即加、减、乘、除法。

所述的密钥K一旦生成，只存储在客户端，不允许外部程序或者非授权访问者访问密钥，也不会以任何形式发送或者传输密钥。因此，数据加密和解密运算都必需在客户端本地完成。

所述的客户端进一步优选具有完备的密钥访问控制机制，例如密钥保存在专有的加密存储芯片中，读取密钥时需要访问口令验证、或指纹验证等身份验证手段确保访问者拥有相应权限。

技术效果

与现有技术相比，本发明最大的改进在于同态运算的计算效率和密文存储空间需求：本发明加密算法的明文空间为整个实数集R，密文空间为Rⁿ，n＝5时即可以提供足够的安全性。整个密文存储空间的需求大大小于现有技术。针对普通数值类型的明文，加密算法只要进行一 次计算就可以得到密文，而现有技术则需要进行反复迭代运算，这大大加快了加密解密的运算速度。同时，针对密文的同态运算，本发明方法的运算过程也具有更快的速度，更少的迭代步骤，运算结果的密文扩展速度也大大小于现有技术。

此外，在云计算服务被广泛应用的大背景下，本发明的同态加密技术可以使得数据的真实取值仅对拥有密钥的数据所有者可见，而对于不能保证其安全性的数据存储方、数据传输管道和数据运算方，均以密文的形式出现，存储、传输和运算提供方只提供对应的存储空间、传输带宽和计算能力，却完全不知道数据的真实取值。计算的结果仍旧用密文表达，数据拥有者凭借密码就可以进行解密，从而得到所要的正确结果。

附图说明

图1为本发明基本应用示意图。

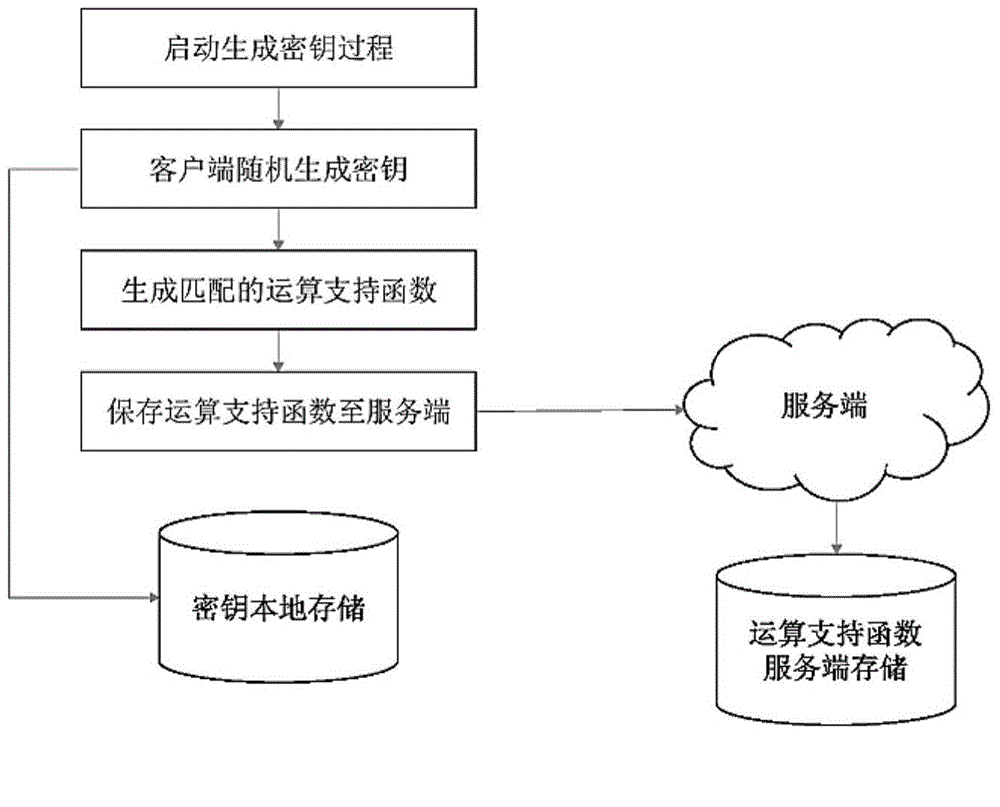
图2为本发明密钥生成过程示意图。

图3为实施例数据加密过程示意图。

图4为实施例密文同态运算过程示意图一。

图5为实施例密文同态运算过程示意图二。

图6为实施例数据解密过程示意图。

具体实施方式

下面对本发明的实施例作详细说明，本实施例在以本发明技术方案为前提下进行实施，给出了详细的实施方式和具体的操作过程，但本发明的保护范围不限于下述的实施例。

实施例1

本发明对应于不同的需求环境和应用场景可采用多种方式实现，包括：USBKey实现方式、API实现方式、SDK实现方式、芯片实现方式、扩展卡实现方式、专用设备实现方式等。如图1和图2所示，任意一种实现方式中均包括：客户端和服务器端，典型的同态加密运算过程的步骤如下：

1)客户端调用本地存储的密钥对敏感明文数据进行加密，获得密文；

2)客户端将密文以及运算要求发送到服务端，密钥保留于客户端；

3)服务端调用对应的运算支持函数族，并使用同态运算功能，对客户端上传的密文进行其所要求的运算操作，随后返回运算结果密文；

4)客户端接收结果密文，调用本地密钥进行解密，并输出结果明文。

这样的过程中，密钥和明文数据仅仅出现在客户端，而整个传输、运算、存储操作中数据始终以密文的形式存在，因此不存在数据泄露的可能。

以下就上述同态加密运算进行详细说明：

第一步、在客户端生成由函数密钥部分以及多项式密钥部分组成的密钥，具体如下：

1.1)随机选择若干种一元或多元函数，并针对每个一元或多元函数随机生成参数进行线性组合或者复合组合，形成函数密钥部分，即f()。

所述的一元函数包括但不限于：各种解析函数，例如：正比例函数、反比例函数、正弦函数、余弦函数、对数函数、指数函数、幂函数等。

如采用一元正弦函数sin(x)和一元幂函数x³进行线性组合可以组成函数密钥f(x)＝10sin(6x)+5x³，也可以进行复合组合得到函数密钥f(x)＝12sin(8x³+6)。

当需要提高加密强度时，可以选择二元或多元函数构成函数密钥部分，以二元函数为例：f(m_i,n_j),i∈I,j∈I，相应的密文会多一个维度，即C＝{A,M,N,B}，同时运算支持函数族G会变得更加复杂，相应密钥强度更高，但是相应运算量也更大。

所述的函数密钥部分是一个可微的函数，同时其定义域内取值应该大于0。

本实施例中优选采用变化相对平缓的函数密钥部分。

所述的变化是指：其中：D为f()的定义域，K为正实数即平缓指数。

本实施例中优选平缓指数小于等于10。

本实施例中通过在客户端中实现的密钥生成算法中预置一个符合要求的基础函数列表，在生成时可以随机的组合这些基础函数，来获得函数密钥部分的函数形式。

1.2)随机生成多项式密钥部分Y＝{y_i|i∈I}，从而构成完整密钥，即K＝{f(),Y}。

本实施例中优选要求多项式密钥部分y_i均为正整数。

所述的密钥可以保存在客户端本地的任何加密介质中，例如加密文件，加密芯片，U盾或者其他同类存储器内。

1.3)客户端或服务器端通过函数拟合生成运算支持函数族G＝{g₁,g₂,g₃}，并由服务器端保存，由于每个运算支持函数族G都是与一个函数密钥部分相对应的，在服务端在收到运算支持函数族G的同时，需要记录其所对应的用户，即密文发送端的唯一标识。

所述的拟合生成可以直接在客户端进行，并将拟合结果，即运算支持函数族G的表达式传输到服务器端；也可以在客户端进行运算支持函数族G的离散采样，并将采样点数据输出至服务器端，由服务器端根据局部拟合策略或者动态局部拟合策略计算得到运算支持函数族G；

由于计算机运算时，针对浮点数的运算有一个精度的问题。因此所述的拟合可根据具体硬件设置在初始化时设置所需的精度。

所述的运算支持函数族G包括

其中：α、β∈X，h₁(α,β)和h₂(α,β)为满足h₁(α,β)≠h₂(α,β)≠α≠β的任意函数。

本实施例中取h₁＝α+β+1，h₂＝α+β+2，α>0，β>0。

所述的运算支持函数族G优选不以表达式的形式出现以提高本发明的安全性；进一步优选为以数值拟合的方式表达运算支持函数族G。

在某些情况下，例如函数密钥部分f本身不够复杂时，仍可以通过一些运算量十分巨大的方法进行一定程度的破解，通过运算支持函数族G局部还原出函数密钥部分f。因此可以定义各种G的变形，来提高安全性，这样的变形可以有很多种。

所述的数值拟合是指：通过对运算支持函数族G的定义域进行广泛、密集的离散采样，记录每个采样点所对应的G的取值，然后通过曲面拟合技术对G进行近似表达；本实施例中使用曲面拟合技术以及数值计算技术实现，例如使用最小二乘法进行曲面拟合。

当运算支持函数族G的曲面过于复杂，所述的数值拟合可以采用局部拟合再拼接或者采用动态局部拟合的策略得到，即在需要进行求值运算时，针对求值点附近的曲面邻域做局部曲面拟合，得到最终的取值。

仅仅通过运算支持函数族G的拟合表达式或者离散取值点信息，在不知道原函数f具体形式的情况下，要还原出f的表达式是非常困难的。这也是本发明加密方法的安全性保障之一。

这里所描述的是密钥生成过程，即客户端初始化过程。该过程只在某用户第一次使用本系统前进行初始化，以后使用中只需直接访问已生成的密钥即可。

第二步、如图3所示，通过上述生成的密钥对敏感数据进行加密，具体如下：

本实施例中需要加密的数据为一个产品的生产成本P₁和该产品的一个销售合同总报价P₂，这两个数据都是浮点型数值数据。

2.1)针对函数密钥部分f()，在其定义域中随机选择一个自变量x_i，得到该点的函数值f(x_i)，然后乘以多项式密钥的对应分量，得到f(x_i)·y_i，i∈I且I为多项式密钥维度的下标集合。

所述的多项式密钥维度的集合内的每一个元素是一个正整数，最大取值为2就可以满足 安全性要求，可以视加密强度要求进行增加，一般建议最大取值不要超过10。如果最大取值为4，则I等于集合{1，2，3，4}。

2.2)随机选取a_i，得到密文多项式的一个项，a_i·f(x_i)·y_i。

2.3)重复步骤2.1～2.2，直到遍历集合I，并最终得到

2.4)通过公式1)得到B，至此，密文的所有分量A＝{a_i|i∈I}、X＝{x_i|i∈I}以及B均已得到。使用该过程得到前述明文P₁、P₂对应的密文C₁、C₂。

当所述的函数密钥部分为二元函数时，则对应的密文为C＝{A,M,N,B}，相应加密强度得到大幅度提升。

第三步、如图5所示，当服务器端获得多个密文后，基于保存于服务器端的运算支持函数族G对密文进行包括加、减、乘、除的同态运算。

i)以同态运算中的加减法为例。假设某企业需要计算产品销售合同的毛利，其中，产品的生产成本为敏感数据，其密文为C₁；合同的总报价为敏感数据，其密文为C₂；产品销售数量为公开招标的非敏感数据，无需加密，其取值为100，则可以计算得到该合同的毛利为密文C₃，即C₃＝C₂-100·C₁，服务器通过依次计算100·C₁和C₂-100·C₁，即可得到毛利C₃，即C₃＝{A₃,X₃,B₃}，其中：

A₃＝{a_3i|i∈I},a_3i＝a_2i·g₂(x_1i,x_2i)-100·a_1i·g₁(x_1i,x_2i)

X₃＝{x_3i|i∈I},x_3i＝h₁(x_2i,x_1i)

B₃＝B₂-100·B₁

所述的同态加密计算的结果可以以密文方式保存在数据库中，并且在之后的其他运算中使用，而不需要了解该密文的真实取值，只需要在表单显示或者报表打印时，针对拥有密钥的授权用户，在客户端调用解密算法，还原出明文即可。

ii)以同态运算中的乘法为例，假设某企业同时与若干客户签订内容相同的上述产品销售合同，其合同数量为敏感数据，密文为C₄，则总的毛利C₅为：C₅＝C₃·C₄，C₅＝{A₅,X₅,B₅}，其中：

A₅＝{a_5ij|i∈I,j∈I}∪{B₄·a_3i|i∈I}∪{B₃·a_4j|j∈I},a_5ij＝a_3i·a_4j·g₃(x₃,x₄)

X₅＝{x_5ij|i∈I,j∈I}∪{x_3i|i∈I}∪{x_4j|j∈I},x_5ij＝h₂(x_3i,x_4j)

B₅＝B₃·B₄

iii)以同态运算中的除法为例，使用多项式除法运算法则，引入分式表达，增加分母多项式之后，把除法转化为加法和乘法的组合，最终得到计算结果。因此，在有除法运算的环境下，更加一般的明文表达式应该是分式形式如：

密文具体表达为：

$P_a=\frac{P_1}{P_2}=\frac{\underset{i\∈I}{\mathrm{\Σ}}{a}_{1i}\·f\left(c_{1i}\right)\·y_i+B_1}{\underset{i\∈I}{\mathrm{\Σ}}{a}_{2i}\·f\left(x_{2i}\right)\·y_i+B_2}$

C_a＝{A₁,X₁,B₁,A₂,X₂,B₂}

$P_b=\frac{P_3}{P_4}=\frac{\underset{i\∈I}{\mathrm{\Σ}}{a}_{3i}\·f\left(c_{3i}\right)\·y_i+B_3}{\underset{i\∈I}{\mathrm{\Σ}}{a}_{4i}\·f\left(x_{4i}\right)\·y_i+B_4}$

C_b＝{A₃,X₃,B₃,A₄,X₄,B₄}

则除法C_r＝C_a/C_b的结果C_r＝{A₅,X₅,B₅,A₆,X₆,B₆}是：

A₅＝{a_5ij|i∈I,j∈I}∪{B₃·a_1i|i∈I}∪{B₁·a_3j|j∈I},a_5ij＝a_1i·a_3j·g₃(x₁,x₃)X₅＝{x_5ij|i∈I,j∈I}∪{x_1i|i∈I}∪{x_3j|j∈I},x_5ij＝h₂(x_1i,x_3j)B₅＝B₁·B₃

A₆＝{a_6ij|i∈I,j∈I}∪{B₄·a_2i|i∈I}∪{B₂·a_4j|j∈I},a_6ij＝a_2i·a_4j·g₃(x₂,x₄)X₆＝{x_6ij|i∈I,j∈I}∪{x_2i|i∈I}∪{x_4j|j∈I},x_6ij＝h₂(x_2i,x_4j)B₆＝B₂·B₄

分式形态下，进行密文同态加法运算时，需要先进行通分，即一个密文的分子部分乘以另一个密文的分母部分作为新的分子，然后与同样运算后的另一个密文的新的分子部分进行加法运算，得到结果的分子。同时，将两个密文的分母部分相乘作为结果的分母，化简后得到最终结果。

分式形态下，进行密文同态乘法运算时，将两个密文的分子部分与分母部分分别相乘，作为新的分子和分母，化简后得到最终结果。

第三步中的服务器端在进行同态运算时，可采用基于密文ID的方式经检索到预存的密文后进行同态计算，或直接通过接受客户端发出的密文和运算符进行同态计算。

所述的密文ID是指对应预存密文的ID号码，该ID号码优选保存于客户端。

如图4所示，为使用密文ID的同态运算过程，其具体步骤包括：

1)客户端获取运算指令，包含需要参与运算的密文ID，以及需要进行的运算操作符和其他参数。

2)发送密文ID、同态运算操作符和运算参数到服务端，用以检索出对应的密文，等待进行运算，服务端收到指令后，首先读取对应的运算支持函数族，然后根据运算指令对前一步检索出的密文进行同态运算。

3)服务端将同态运算的结果返回运算请求方，该运算结果仍旧是密文的形式。

如图5所示，为直接使用密文，而非密文ID的同态运算过程，其具体步骤包括：

i)获取运算指令，包含待运算的密文，运算操作符，以及其他参数。

ii)将密文、运算操作符、运算参数等数据发送到服务端。

iii)服务端获取运算指令后，读取对应的运算支持函数族，并完成对密文的运算要求，得到运算结果密文。

iv)服务端将运算结果返回给运算请求方。

第四步、如图6所示，当客户端获得来自服务器端的同态运算后的结果密文时，将结果密文代入加密公式(1)中，即可获得对应的明文结果。

当原始明文数据为数值型，则上一步的解密结果即是最终结果，否则还需要进行类型转换，才能得到最终解密结果。

实施例2

本实施例与实施例1不同之处在于，其采用的运算支持函数G包括：

其中：α、β∈X，h₁(α,β)、h₂(α,β)和h₃(α,β)为满足h₁(α,β)≠h₂(α,β)≠h₃(α,β)≠α≠β的任意函数；

对应的同态运算具体包括：

i)密文与密文的加减法：C_r＝C₂±C₁，C_r＝{A_r,X_r,B_r}，其中：

$A_r=\left\{a_{\mathrm{ri}}\right|i\∈I\},a_{\mathrm{ri}}=a_{2i}\·g_1(x_{2i},x_{1i},\±\frac{a_{1i}}{a_{2i}})/h_3(\±\frac{a_{1i}}{a_{2i}}),$

X_r＝{x_ri|i∈I},x_ri＝h₁(x_2i,x_1i)，

B_r＝B₂±B₁；

ii)密文与密文的乘法：C_r＝C₃·C₄，C_r＝{A_r,X_r,B_r}，其中：

A_r＝{a_rij|i∈I,j∈I}∪{B₄·a_3i|i∈I}∪{B₃·a_4j|j∈I},a_rij＝a_3i·a_4j·g₂(x₃,x₄)，

X_r＝{x_rij|i∈I,j∈I}∪{x_3i|i∈I}∪{x_4j|j∈I},x_rij＝h₂(x_3i,x_4j)，

B_r＝B₃·B₄；

iii)密文与密文的除法：C_r＝C_a/C_b，C_r＝{A₅,X₅,B₅,A₆,X₆,B₆}，其中：

A₅＝{a_5ij|i∈I,j∈I}∪{B₃·a_1i|i∈I}∪{B₁·a_3j|j∈I},a_5ij＝a_1i·a_3j·g₂(x₁,x₃)，

X₅＝{x_5ij|i∈I,j∈I}∪{x_1i|i∈I}∪{x_3j|j∈I},x_5ij＝h₂(x_1i,x_3j)，

B₅＝B₁·B₃，

A₆＝{a_6ij|i∈I,j∈I}∪{B₄·a_2i|i∈I}∪{B₂·a_4j|j∈I},a_6ij＝a_2i·a_4j·g₂(x₂,x₄)，

X₆＝{x_6ij|i∈I,j∈I}∪{x_2i|i∈I}∪{x_4j|j∈I},x_6ij＝h₂(x_2i,x_4j)，

B₆＝B₂·B₄。

在本实施例中，g₁变为三元函数，相应的其拟合计算量就会增加不少，对f的平缓度和复杂度要求也更高，但是对应的安全性较二元函数也会大幅提高。

实施例3

本实施例为了提高安全性，在生成运算支持函数G时引入函数f₂，这个函数不需要添加至密钥中，仅仅影响运算支持函数G的计算和表达，可以理解为对运算支持函数G做了加密。

具体表达式如下：其中：α、β∈X，h₁(α,β)、h₂(α,β)、h₃(α,β)和h₄(α,β)为满足h₁(α,β)≠h₂(α,β)≠h₃(α,β)≠h₄(α,β)≠α≠β的任意函数；f₂()为用于对运算支持函数进行加密的随机生成函数，

对应的同态运算具体包括：

i)密文与密文的加减法：C_r＝C₂±C₁，C_r＝{A_r,X_r,B_r}，其中：A_r＝{a_ri|i∈I},

a_ri＝g₆·[a_2i·g₁(x_2i,x_1i)·g₃(h₁(x_2i,x_1i),h₂(x_2i,x_1i))±a_1i·g₂(x_2i,x_1i)·g₄(h₁(x_2i,x_1i),h₂(x_2i,x_1i))]，

X_r＝{x_ri|i∈I},

x_ri＝h₆(h₄(h₁(x_2i,x_1i),h₂(x_2i,x_1i)),h₃(h₁(x_2i,x_1i),h₂(x_2i,x_1i)))，

B_r＝B₂±B₁；

ii)密文与密文的乘法：C_r＝C₃·C₄，C_r＝{A_r,X_r,B_r}，其中：

A_r＝{a_rij|i∈I,j∈I}∪{B₄·a_3i|i∈I}∪{B₃·a_4j|j∈I},a_rij＝a_3i·a_4j·g₅(x₃,x₄)，

X_r＝{x_rij|i∈I,j∈I}∪{x_3i|i∈I}∪{x_4j|j∈I},x_rij＝h₅(x_3i,x_4j)，

B_r＝B₃·B₄；

iii)密文与密文的除法：C_r＝C_a/C_b，C_r＝{A₅,X₅,B₅,A₆,X₆,B₆}，其中：

A₅＝{a_5ij|i∈I,j∈I}∪{B₃·a_1i|i∈I}∪{B₁·a_3j|j∈I},a_5ij＝a_1i·a_3j·g₅(x₁,x₃)，

X₅＝{x_5ij|i∈I,j∈I}∪{x_1i|i∈I}∪{x_3j|j∈I},x_5ij＝h₅(x_1i,x_3j)，

B₅＝B₁·B₃，

A₆＝{a_6ij|i∈I,j∈I}∪{B₄·a_2i|i∈I}∪{B₂·a_4j|j∈I},a_6ij＝a_2i·a_4j·g₅(x₂,x₄)，

X₆＝{x_6ij|i∈I,j∈I}∪{x_2i|i∈I}∪{x_4j|j∈I},x_6ij＝h₅(x_2i,x_4j)，

B₆＝B₂·B₄。

这样的运算支持函数G可以避免对三元函数进行拟合的庞大运算量，同时也大大提高了安全性。其中，f₂仅在初始化过程中计算G的时候随机生成，对f₂的形式要求尽量简单，避免使用过于复杂的表达式。同时f₂的表达式既不需要保存在客户端，也不需要保存在服务器端，因此在初始化过程后可以直接丢弃。这样既不影响客户端的加密、解密操作，也不影响服务器端的同态运算操作，因此这种情况下G的安全性就非常高，想要通过G还原出函数密钥f的难度将更大。