OFDM压缩感知信道与非线性失真联合估计算法的制作方法

本发明属于无线通信
技术领域：
，涉及一种无线信道估算算法，特别涉及一种OFDM压缩感知信道与非线性失真联合估计算法。
背景技术：
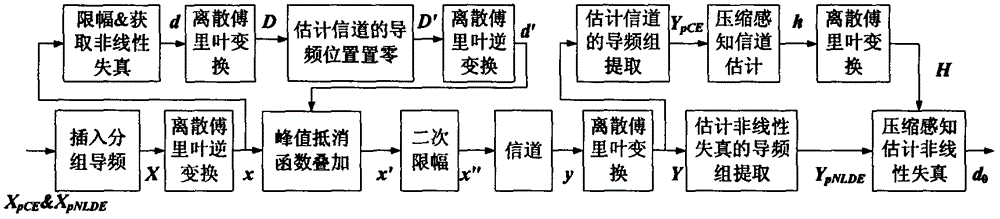
：正交频分复用(OrthogonalFrequencyDivisionMultiplexing，OFDM)具有频带利用率高、抗符号串扰能力强、抗频率选择性衰落能力强等优点，是高速无线通信领域的核心。信道估计与降低峰均比是OFDM系统的两大关键技术。信道估计的精度直接影响衰落信道下的系统性能，高峰均比导致信号经过功率放大器时产生非线性失真(nonlineardistortion，NLD)。目前，已有大量关于OFDM信道估计的研究，其中基于辅助信息的信道估计研究最为广泛，典型方法有最小二乘(leastsquares，LS)、最小均方误差(minimummean-squarederror，MMSE)、线性最小均方误差(linearminimummean-squarederror，LMMSE)估计等。近年来，随着压缩感知理论的提出，大量学者开始探究将其应用于无线通信领域，并对其用于导频辅助的OFDM信道估计进行研究。研究表明，在稀疏信道下基于相同数量的导频可以比传统方法达到更好的估计性能。然而，已有的信道估计方法大多未考虑OFDM信号非线性的影响，认为信号不存在非线性失真或已通过降低峰均比算法得到良好解决。目前，降低峰均比的典型方法有预失真法、部分传输序列法、选择映射法等，其在发射机中实施且多数具有较高的复杂度。2003年，一种基于信号重建的迭代方法被提出用以在接收机中估计和消除非线性失真。2005年，Tropp等人提出将压缩感知用于OFDM系统的脉冲噪声消除，基于导频估计脉冲噪声。2014年，A.Ghassemi等人进一步提出OFDM信号的非线性失真可以看作稀疏的加性噪声，可利用压缩感知在接收机中对其进行估计与补偿。上述方法可避免发射机中实施降低降均比算法，但均未考虑衰落信道对NLD估计的影响。在非线性OFDM系统中，基于带有非线性失真的辅助信息无法进行准确的信道估计，而衰落信道又严重影响NLD估计性能，信道估计与NLD估计相互影响相互制约成为二者联合估计的难点。近年来，已有少量学者开始研究非线性OFDM系统的信道与NLD联合估计问题。例如基于迭代的联合算法，基于LS和DFT插值进行信道估计，基于判决反馈和信号重构进行NLD消除。该方法的估计精度受导频数量和错误判决的影响，且需已知发射机限幅操作的先验信息，接收机实施信号重构增加了系统复杂度。基于LMMSE结合压缩感知的迭代联合估计也被提出，但LMMSE算法复杂度较高，且需已知信道先验信息。上述联合估计方法均需要信道或限幅的先验信息，使其适用范围受到限制。技术实现要素：本发明的目的是针对OFDM系统信道估计及高峰均比问题，利用信道与NLD的双重稀疏性，提出了一种基于压缩感知的非线性OFDM系统的信道估计与NLD恢复联合算法。该算法具有良好的估计性能，同时可避免系统实施复杂的降低峰均比算法，且无需迭代运算及先验信息。为了达到以上效果，本发明OFDM压缩感知信道与非线性失真联合估计算法，包括下列步骤：步骤1：构建存在多径信道与NLD影响时的OFDM解调信号模型；步骤2：在发送端分组导频与级联限幅，以保护导频信息不受非线性失真影响；步骤3：利用信道与非线性噪声脉冲的双重稀疏性，在接收端利用压缩感知进行信道与NLD联合估计。采用OFDM压缩感知信道与非线性失真联合估计算法可避免系统实施复杂的降低峰均比算法，且无需迭代运算及先验信息，具有良好的估计性能。附图说明：为了更清楚的说明发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单的介绍，下面描述中的附图仅仅是本发明的一个实施例，对于本领域普通技术人员来讲，在不付出创造劳动性的前提下，还可以根据附图获得其他的附图。图1是本发明分组导频结构示意图；图2是本发明联合算法原理框图；图3是不同信噪比下各联合算法的信道估计性能；图4是不同信噪比下各联合算法的非线性失真估计性能；图5是不同限幅门限下各联合算法的信道估计性能；图6是不同限幅门限下各联合算法的非线性失真估计性能；图7是不同信噪比下各联合算法的系统误比特率；图8是不同限幅门限下各联合算法的系统误比特率。具体实施方式：本发明的主旨是提出一种OFDM压缩感知信道与非线性失真联合估计算法，利用信道与非线性失真的双重稀疏性，避免系统实施复杂的降低峰均比算法，降低系统的复杂度。下面结合附图对本发明实施方式作进一步详细描述。一、OFDM系统模型的构建在OFDM系统中，频域信号X＝[X0，x1，...，XN-1]T经过IDFT调制的时域信号可表示为xn=1NΣk=0N-1Xkej2πkn/N,n=0,1,...,N-1---(1)]]>定义向量x＝[x0，x1，...，xN-1]T，则(1)式可表示为矩阵形式x＝QX(2)式中，Q为N×N维逆傅里叶变换矩阵。Qm,n=1Nej2π(m-1)(n-1)/N,1≤m≤N,1≤n≤N---(3)]]>在N点数据前加入长为Ng的循环前缀组成完整OFDM符号经DAC输出。信号经过功率放大器时由于其线性度的限制产生NLD，引入NLD的信号可表示为x′n＝βxn+dn(4)式中，β为使xn与dn不相关的常数。定义向量d＝[d0，d1，...，dN-1]为引入的NLD，其可看作稀疏的加性噪声。为分析方便，本发明中令β为1，则引入NLD的信号可表示为x′＝x+d＝QX+d(5)为使放大器工作于线性区域，在发送端对信号进行限幅处理，则经过限幅的时域信号可表示为xn′=xn,|xn|≤AAxn/|xn|,|xn|>A---(6)]]>式中，A为归一化限幅门限。受多径信道影响，接收信号可表示为y=h⊗x′+z=h⊗(x+d)+z---(7)]]>式中，表示循环卷积运算，z＝[z0，z1，...，zN-1]T表示加性高斯白噪声，h＝[h0，h1，...，hL-1，01×(N-L+1)]T，其中hl，l＝0，1，...，L-1为信道冲击响应(CIR)。经过DFT解调所得频域信号可表示为Yk=Σn=0N-1yne-j2πnk/N,k=0,1,...,N-1---(8)]]>定义向量Y＝[Y0，Y1，...，YN-1]T，则将(7)式写为矩阵形式Y＝QHy＝HX+HQHd+Z(9)式中，QH为N×N维傅里叶变换矩阵，H＝diag(H0，H1，...，HN-1)为信道频域响应向量QHh变形而成的对角矩阵，Z＝QHz为高斯白噪声的频域形式。式(8)即为同时存在多径信道与NLD影响时的OFDM解调信号模型。二、发送端加入分组导频与级联限幅图1是本发明分组导频结构示意图，图2是本发明联合算法原理框图；为利用压缩感知同时估计信道与非线性失真，设计两组梳状导频：第一组用于信道估计，定义为向量XpCE＝[XpCE，1，XpCE，2，...，XpCE，S]，S为信道估计导频组长度；第二组用于NLD估计，定义为向量XpNLDE＝[XpNLDE，1，XpNLDE，2，...，XpNLDE，R]，R为NLD估计导频组长度。为消除信道估计导频组所受NLD的影响，提高信道估计精度，本发明在传统限幅法的基础上提出在系统发送端进行级联限幅，以减小限幅带来的导频处NLD噪声。对时域OFDM信号xn进行限幅并求出限幅失真噪声dn=0,|xn|≤AAxn/|xn|-xn,|xn|>A---(10)]]>式中，A为限幅门限值。对向量d＝[d0，d1，...，dN-1]T进行FFT变换可得D＝QHd(11)式中，QH为傅里叶变换矩阵。将D中与信道估计分组导频位置相对应的元素置为0得到D’，以消除NLD噪声影响，再将D’变换到时域d′＝QD′(12)式中，Q为逆傅里叶变换矩阵。对OFDM信号x＝[x0，x1，...，xN-1]T叠加变换后的限幅失真向量得到x′＝x+d′(13)从而完成第一次限幅操作。上述频域置零操作会使第一次限幅后的信号产生一定程度的峰值回升，需对其进行第二次限幅使不超过门限值Axn′′=0,|xn′|≤AAxn′/|xn′|,|xn′|>A---(14)]]>设二次限幅产生的NLD噪声为d″，则二次限幅后的信号可以表示为x″＝x′+d″＝x+d′+d″(15)第二次限幅会使频域信道估计导频处重新产生NLD，但此时的NLD噪声影响已大幅减小，本发明采用二次级联限幅。三、接收端利用压缩感知进行信道与NLD联合估计接收端首先基于分组导频XpCE进行信道估计，再以信道信息为先验信息利用分组导频XpNLDE估计信号的非线性失真。将(14)式代入前文信号模型(6)式后进行傅里叶变换可得Y＝HX+HQHd′+HQHd″+Z(16)选取信道估计导频所在的行可得YpCE=HpCEXpCE+HpCEQpCEHd′+HpCEQpCEHd′′+ZpCE---(17)]]>由于第一次限幅使得上式可简化为YpCE=HpCEXpCE+HpCEQpCEHd′′+ZpCE---(18)]]>由于第二次限幅后导频处的噪声影响已很小，这里将上式第二项归并到噪声项中，则YpCE＝HpCEXpCE+ZpCE′(19)为进一步整理为压缩感知基本形式，将上式改写为YpCE=XpCE′HpCE′+Z′=XpCE′QpCEHh+ZpCE′---(20)]]>式中，XpCE′＝diag(XpCE，1，XpCE，2，...，XpCE，Q)，HpCE′＝[HcCE，1，HpCE，2，...，HpCE，Q]，h为信道CIR。利用压缩感知采用压缩感知算法对(19)式中的h进行求解，即h^=argmin||h||1s.t.||XpCE′QpCEHh^-YpCE||2≤ϵ---(21)]]>对估计出的进行傅里叶变换得到频域信道响应代入前文(15)式并选取NLD估计导频所在的行可得YpNLDE=H^pNLDEXpNLDE+H^pNLDEQpNLDEH(d′+d′′)+ZpNLDE---(22)]]>将上式改写为VpNLDE=YpNLDE-H^pNLDEXpNLDE=H^pNLDEQpNLDEHd0+ZpNLDE---(23)]]>同样利用压缩感知采用压缩感知算法求解NLD噪声d0，即d^0=argmin||d0||1s.t.||H^pNLDEQpNLDEHd^0-VpNLDE||2≤ϵ---(24)]]>四、实例分析为验证本发明算法性能搭建OFDM系统，包含512个子载波，其中包括70个导频子载波，循环前缀长度为64，采用64QAM调制及5/8LDPC编码，离散信道长度为42，有6个有效径，用于信道估计的导频数选取22，用于非线性失真估计的导频数选取48。为体现本发明算法的性能，与现有算法在同一系统中进行性能比较，其中算法1为基于LS和DFT插值进行信道估计，基于判决反馈和信号重构进行NLD消除；算法2为基于LMMSE结合压缩感知的迭代联合估计。图3是不同信噪比下各联合算法的信道估计性能，图4是不同信噪比下各联合算法的非线性失真估计性能，限幅门限2.5dB；图5是不同限幅门限下各联合算法的信道估计性能，图6是不同限幅门限下各联合算法的非线性失真估计性能，信噪比为25dB。当信噪比较高时(大于15dB)，本发明算法的信道估计性能明显优于现有算法1、算法2，且十分接近无非线性失真的压缩感知信道估计性能；在非线性失真估计方面，本算法性能明显优于现有算法1、算法2。图7是不同信噪比下各联合算法的系统误比特率，限幅门限为2.5dB。可以看出，当信噪比较低时，三种算法的系统误比特率相近，而当信噪比大于21dB时，本发明算法的系统误比特率明显小于算法1、算法2。图8是不同限幅门限下各联合算法的系统误比特率，信噪比25dB。可以看出，在信噪比较高时，本发明算法在不同限幅程度下的系统误比特率均明显小于算法1、算法2，体现了本文联合算法在较高信噪比下的优势。实例结果表明，该算法具有良好的估计性能，同时可避免系统实施复杂的降低峰均比算法，且无需迭代运算及先验信息，对OFDM系统信道估计有很好的利用价值。以上所述仅为本发明的较佳实施例，并不限制本发明，凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。当前第1页1 2 3