大规模MIMO系统中信号检测装置及方法与流程

本发明涉及通信技术领域，特别涉及一种大规模MIMO系统中信号检测装置及方法。

背景技术：

大规模多输入多输出(MIMO)在实现高频谱密度和无线通信的可靠性方面是一种新兴技术，在未来无线通信产业(如5G)，该技术视为推动产业发展的关键技术。首先，大规模多输入多输出系统可以实现多数据流在同一频带中同时传输，有效改善频谱资源稀缺问题。系统分为上行、下行链路两个部分，其中，上行链路由多个用户天线向基站的多个天线传输信号。由于不同天线间的干扰与信道噪声，基站一端需要对接收到的信号进行解码，其实质为求解线性方程组。其次，由于未来无线通信对数据吞吐量与传输延迟的要求越来越高，基站端的信号解码必须能够快速高效地完成，同时为了保证数据传输的可靠性，必须保持较低的误码率。

然而MIMO技术一个的最大挑战就是上行链路信号的检测。相关技术中，一些优化非线性算法例如极大似然法(ML)、固定复杂度球形译码(FSD)、K-Best、禁忌搜索(TS)被用来减少计算的复杂度获得高的探测精度，但这些算法在基站拥有数百根天线的MIMO系统中计算复杂度仍然很高。

为了降低计算的复杂度，可以应用线性算法，其中最小均方误差(MMSE)是一种最有效可行的方法，该种算法可以有效降低计算复杂度并同时保证最小的精度损失。不过，随着用户数量的增加，MMSE存在非常复杂的矩阵求逆和矩阵乘法运算，导致大大降低系统的运行速度。这种方法运用乔里斯基分解、共轭梯度(CG)、纽曼级数近似等方法来降低其运算的复杂度，但所有的元素很难进行并行的计算，导致大大限制了硬件资源。

切比雪夫迭代算法被认为是最有可能解决大型线性方程组求解问题的解决方案，然而仍然有三个主要障碍限制了其在MIMO中的应用。首先，需要计算过多的关联特征值参数，导致会浪费大量的硬件资源和运行速度；其次，大范围的乘法在迭代前会导致影响整个检测系统的效率；最后，很难找到切比雪夫迭代的初始值。因此，有待改进。

技术实现要素：

本发明旨在至少在一定程度上解决相关技术中的技术问题之一。

为此，本发明的一个目的在于提出一种大规模MIMO系统中信号检测装置，该装置可以提高了检测效率，简单便捷。

本发明的另一个目的在于提出一种大规模MIMO系统中信号检测方法。

为达到上述目的，本发明一方面实施例提出了一种大规模MIMO系统中信号检测装置，包括：初始值产生模块，用于获取平稳瑞利分布信道矩阵H、基站段接收信号向量y与噪声的功率密度N₀，以基于信道矩阵的渐进正交性并参照特征值得到预处理后的迭代参数、切比雪夫迭代算法的初始值与匹配滤波后y^MF；第一至第三迭代模块，用于根据所预处理后的迭代参数、切比雪夫迭代算法的初始值与匹配滤波后y^MF依次计算评估传递向量U*B矩阵的值H^H，B*1的残差r^(k)，修正向量σ^(k)，和评估传递向量评估模块，用于根据评估传递向量与所述预处理后的迭代参数得到最大对数似然比LLR，以得到用户设备发送的原始数据。

本发明实施例的大规模MIMO系统中信号检测装置，考虑到信道矩阵的渐进正交性，并且利用特征值产生切比雪夫迭代算法的初值，利用了近似计算规避大规模矩阵转置、相乘带来的计算量，以及根据大规模多入多出系统的属性，提高了收敛速度，实现了大规模多输入多输出无线通信系统中的算法，充分利用了数据并行性计算，实现了高速低功耗的检测译码，提高了检测效率。

另外，根据本发明上述实施例的大规模MIMO系统中信号检测装置还可以具有以下附加的技术特征：

进一步地，在本发明的一个实施例中，基站天线数为B，由B行S列的信道矩阵H表示无线通信信道，其中，H中的元素符合平坦瑞利衰落分布。

进一步地，在本发明的一个实施例中，所述第一至第三迭代模块进一步用于计算迭代k次的残余向量r^(k)和评估信号

进一步地，在本发明的一个实施例中，迭代模块采用用户级流水线结构。

为达到上述目的，本发明另一方面实施例提出了一种大规模MIMO系统中信号检测方法，包括以下步骤：获取平稳瑞利分布信道矩阵H、基站段接收信号向量y与噪声的功率密度N₀，以基于信道矩阵的渐进正交性并参照特征值得到预处理后的迭代参数、切比雪夫迭代算法的初始值与匹配滤波后y^MF；根据所预处理后的迭代参数、切比雪夫迭代算法的初始值与匹配滤波后y^MF依次计算评估传递向量U*B矩阵的值H^H，B*1的残差r^(k)，修正向量σ^(k)，和评估传递向量根据评估传递向量与所述预处理后的迭代参数得到最大对数似然比，以得到用户设备发送的原始数据。

本发明实施例的大规模MIMO系统中信号检测方法，通过在切比雪夫迭代算法的基础上进行优化，可以被命名为可并行切比雪夫迭代算法(Parallelizable Chebyshev Iteration，PCI)，考虑到信道矩阵的渐进正交性，并且利用特征值产生切比雪夫迭代算法的初值，利用了近似计算规避大规模矩阵转置、相乘带来的计算量，以及根据大规模多入多出系统的属性，提高了收敛速度，实现了大规模多输入多输出无线通信系统中的算法，充分利用了数据并行性计算，实现了高速低功耗的检测译码，提高了检测效率。

另外，根据本发明上述实施例的大规模MIMO系统中信号检测方法还可以具有以下附加的技术特征：

进一步地，在本发明的一个实施例中，基站天线数为B，由B行S列的信道矩阵H表示无线通信信道，其中，H中的元素符合平坦瑞利衰落分布。

进一步地，在本发明的一个实施例中，还包括：计算迭代k次的残余向量r^(k)和评估信号

本发明附加的方面和优点将在下面的描述中部分给出，部分将从下面的描述中变得明显，或通过本发明的实践了解到。

附图说明

本发明上述的和/或附加的方面和优点从下面结合附图对实施例的描述中将变得明显和容易理解，其中：

图1为根据本发明一个实施例的大规模MIMO系统中信号检测装置的结构示意图；

图2为根据本发明一个实施例的基于PCI的VLSI顶层结构示意图；

图3为根据本发明一个实施例的大规模多入多出系统模型示意图；

图4为根据本发明一个实施例的多入多出芯片系统构成示意图；

图5为根据本发明一个实施例的PE-A结构示意图；

图6为根据本发明一个实施例的PE-B结构示意图；

图7为根据本发明一个实施例的PE-C结构示意图；

图8为根据本发明一个实施例的初始模块的用户级流水线处理结构示意图；

图9为根据本发明一个实施例的预迭代模块的用户级流水线结构示意图；

图10为根据本发明一个实施例的LLR模块结构示意图；

图11为根据本发明一个实施例的大规模MIMO系统中信号检测方法的流程图。

具体实施方式

下面详细描述本发明的实施例，所述实施例的示例在附图中示出，其中自始至终相同或类似的标号表示相同或类似的元件或具有相同或类似功能的元件。下面通过参考附图描述的实施例是示例性的，旨在用于解释本发明，而不能理解为对本发明的限制。

下面参照附图描述根据本发明实施例提出的大规模MIMO系统中信号检测装置及方法，首先将参照附图描述根据本发明实施例提出的大规模MIMO系统中信号检测装置。

图1是本发明一个实施例的大规模MIMO系统中信号检测装置的结构示意图。

如图1所示，该大规模MIMO系统中信号检测装置10包括：初始值产生模块100、第一至第三迭代模块200和评估模块300。

其中，初始值产生模块100用于获取平稳瑞利分布信道矩阵H、基站段接收信号向量y与噪声的功率密度N₀，以基于信道矩阵的渐进正交性并参照特征值得到预处理后的迭代参数、切比雪夫迭代算法的初始值与匹配滤波后y^MF。第一至第三迭代模块200用于根据所预处理后的迭代参数、切比雪夫迭代算法的初始值与匹配滤波后y^MF依次计算评估传递向量U*B矩阵的值H^H，B*1的残差r^(k)，修正向量σ^(k)，和评估传递向量评估模块300用于根据评估传递向量与预处理后的迭代参数得到最大对数似然比，以得到用户设备发送的原始数据。本发明实施例的检测装置10可以通过将硬件以及操作限制为深度流水线模式，加快了运行速度。另外，经实验表明,，相比于当前最先进的设计，本发明实施例在高能量效率(吞吐率/能耗)、面积效率(吞吐率/面积)方面具有显著优势。

具体地，本发明实施例是对切比雪夫迭代的优化，用以大型线性方程组求解，可以有效加速信号检测，提高数据并行性，增加数据吞吐率。在这个算法中，假设信道矩阵是渐进正交的，切比雪夫迭代的初始值可以通过特征值得到。则切比雪夫迭代可以被用来估计大规模矩阵求逆和矩阵乘法。PCI显著提高了系统的并行度并降低了计算的复杂度。

举例而言，基于PCI，一种超大规模集成电路(VLSI)被设计出来用以完成64-QAM,128*16MIMO系统，其顶层结构如图2所示，整个结构划分为5个部分。该模型可以接收以矩阵形式传递的线性方程组数据信号，并输出该线性方程组的解向量。

第一部分初始值产生模块100：基于信道矩阵的渐进正交性，参照特征值产生切比雪夫迭代算法的初值将接收到的信道模型矩阵计算出迭代所需参数。迭代计算模块接收预处理得到的参数和初始值匹配滤波y^MF。

第二至第四部分分别为迭代模块201、迭代模块202、迭代模块203：依次计算了评估传递向量U*B矩阵的值H^H，B*1的残差r^(k)，修正向量σ^(k)，和评估信号

第五部分综合评估模块300：结合评估传递向量初始模块中的参数β,N₀，计算软输出LLR。

在本发明的实施例中，考虑到信道矩阵的渐进正交性，该算法利用特征值产生切比雪夫迭代算法的初值。此外该算法利用了近似计算规避大规模矩阵转置、相乘带来的计算量；根据大规模多入多出系统的属性，该算法比当前最先进的算法收敛速度更快，且复杂度更低，精度更高。

进一步地，在本发明的一个实施例中，基站天线数为B，由B行S列的信道矩阵H表示无线通信信道，其中，H中的元素符合平坦瑞利衰落分布。

对于MIMO系统而言，如图3所示，图3的简图描述的是无线通信系统，包括了基站和无线设备。无线设备也被称为用户设备，如图中的用户设备1至S。对于多输入多输出系统，同一时间可以有第一至第三用户设备通过无线通信信道与基站进行数据传输。本发明实施例中，假定基站天线数为B，因此无线通信信道可以由B行S列的信道矩阵H表示。为模拟现实环境，H中的元素符合平坦瑞利衰落分布。

进一步地，对应到MIMO芯片结构，如图4所示，图4以框图形式展示了MIMO_CHIP的主要构成：PLL、clk_gen、rst_gen、buffer_ctrl、MEMORY、mimo_top模块组成。其中mimo_top模块为本发明实施例描述的大规模MIMO系统中信号检测装置。

对于上行链路，基站端实现的功能是通过信道矩阵H^u和接收到的信号y^u，计算或者估计原始信号s^u。再经过译码和解调形成最初的向量X。其中接收信号y可以直接由接收天线，而信道矩阵H可以通过已知的导频信号来检测。传统的最小均方误差方法是将加性噪声与信道Gram矩阵求和得到MMSE滤波矩阵A＝(G+N₀E_sI_N)，再求A矩阵的逆矩阵，与匹配滤波后的y^MF相乘得出原始信号。而矩阵求逆是所有计算中运算复杂度最大的。本发明实施例就是立足于改进的切比雪夫算法——可并行切比雪夫迭代算法(Parallelizable Chebyshev Iteration，PCI)，降低运算复杂度、提升计算并行度来计算s^u，使之能更好的用硬件实现。

具体而言，对于大规模多入多出系统，我们假设其基站端的天线数量为B，用户数为U，k为并行切比雪夫迭代算法的迭代次数。这里可以用等式y＝Hs+n来表示上行链路过程。H是信道信息矩阵，n是加性高斯噪声，y是基站接收到的信号，此三者是已知的。而求解原始信号s就是基站解码所要做的工作。

传统的最小均方误差估计(MMSE)算法估算信号的表达式可表示为：

其中A＝H^HH+N₀E_s^-1I_M是一个M阶的厄米特正定矩阵，y^MF＝H^Hy是经过匹配滤波的接收信号。

而PCI算法是针对先行方程As＝y^MF的计算。传统的算法中，为了求解s直接计算A^-1y^MF。可以看出这一方法的主要计算量集中在计算矩阵A的逆上面。不但计算量大，而且非常难实现并行流水线计算。因此这对于由硬件电路实现信号检测解码的实现并不是一个好的办法。

为了使算法更加适合在硬件电路上实现。本发明实施例提出如图2所示的新算法，操作步骤具体如下，其中每一步内的计算相互独立，可以并行计算：

1.系统接收数据：平稳瑞利分布信道矩阵H，基站段接收信号向量y，噪声的功率密度N₀；

2.初值计算：用Massive MIMO矩阵特征值的特点，将α₀、β₀近似为U和B的表达；

3.迭代优化：计算残差和其余参数ρ、ψ，

${\mathrm{\ρ}}^{\left(0\right)}=\frac{2{\mathrm{\α}}^2}{2{\mathrm{\α}}^2-1},{\mathrm{\ρ}}^{\left(k\right)}=\frac{4{\mathrm{\α}}^2}{4{\mathrm{\α}}^2\mathrm{\β}-{\mathrm{\β}}^2{\mathrm{\ρ}}^{(k-1)}};,$

三次迭代修正初值得到更为精确的结果

4.原始数据产生：根据对数似然比LLR最终计算出用户设备发送的原始数据。

进一步地，在本发明的一个实施例中，第一至第三迭代模块200进一步用于计算迭代k次的残余向量r^(k)和评估信号

其中，在本发明的一个实施例中，迭代模块采用用户级流水线结构。

由于检测与解码最终将在集成电路芯片上实现，例如FPGA，ASIC，DSP等等，算法的计算量将是衡量优劣的重要指标。由于不论是纽曼级数近似算法、高斯-赛德尔法算法、共轭梯度算法，还是本发明提出的并行切比雪夫迭代(PCI)算法，乘法器都是决定运算频率的关键路径，并且占整个芯片的绝大部分计算量，因此用算法中实数乘法数量来衡量的算法的优劣，由于硬件电路中乘法器的开销是相对较大的，以此衡量计算量更加客观。

在本发明实施例中，计算量主要有以下四个来源：

1.初值产生(不计入)：初值部分的计算来自于参数的计算，考虑到用户和天线固定的信道矩阵中，这些参数只需要计算一次，并作为常量存储在寄存器中，因此忽略这部分实数乘法；

2.匹配滤波器的向量的计算：即特征值近似解的计算，需要实现一个的矩阵和一个y_B×1的向量的乘法和次矩阵的计算，这里需要用到4BU次实数乘法；

3.三步的计算量：H_B×U矩阵和传播向量的矩阵相乘，残差向量r^(k)的计算，和修正因子δ^(k),分别需要4kBU,4kBU和2kU次的实数乘法；

4.LLR模块：LLR需要用分段函数计算，这里需要U+1次的的实数乘法用以64-QAM。

因此，PCI算法的总的计算量为以上之和：(8k+4)BU+(6k+1)U+1。表1为实数乘法数目比较，如表1所示。

表1

实验表明，最小均方误差(MMSE)算法用柯列斯基分解算法实现的复杂度为o(U³)(即正比于U³)。纽曼级数近似算法在迭代次数k在2以内时，复杂度可达到o(U²)，但是随着k的增加，计算量为o(U³)。此外，在大规模矩阵计算时，其计算量为o(BU²)。当M增大，即用户设备数增多时计算量增加过快，不利于硬件实现。高斯-赛德尔(GS)算法和共轭梯度(CG)算法可以减少逆矩阵的计算量，但是对于大规模矩阵乘法的计算量并没有改善。而本发明提出的PCI算法可在任意迭代次数下将计算量从o(U³)降为o(U²)，其计算量大幅度减少，更利于在大规模多输入多输出系统中使用。

另外，为了更好的说明整个电路的结构，在这里首先介绍构成每个电路模块的最基本的电路单元。

根据系统中不同的三种模块，基本计算单元被分为3种。分别是处理单元(Process Element)A(PE-A)、处理单元B(PE-B)和处理单元C(PE-C)。下面将详细介绍这3种计算单元的结构和功能。

如图5是PE-A的结构框图。其中主要包括了：实部部分、虚部部分和复数部分，并且有两个ALU处理单元，用来对一组二输入进行八次乘法、七次加法和一次累加。PE-A的输入包括一个复数矩阵和一个复数向量，输出为一个复数向量和一组矩阵主对角元素(矩阵与共轭矩阵相乘主对角线元素为实数)构成的实数数组。其组成结构如图ALU阵列组成，中间为两个累加器。

PE-A主要功能包括计算矩阵与向量相乘以及矩阵与自身的共轭转置矩阵的乘积。计算步骤如下：首先输入矩阵H^*和向量y，每个时钟周期可以输入8组数据。经过ALU阵列做乘法。其中上面两个ALU用来计算H^*与y中具体对应元素相乘，其结果经过累加形成最终结果y^MF。下面一个ALU用来计算H^*与自身共轭转置H相乘，经过累加得到最终结果。

如图6是PE-B的结构框图。其中主要包括了：算术逻辑单元ALU，累加器器ACC。PE-B中的ALU与PE-A中的不同，因为PE-B中的ALU不需要进行加法运算。PE-B的输入是一个复数矩阵，输出也是一个复数矩阵。其组成结构如图左侧由四片相同结构的ALU阵列组成，每一片拥有2个ALU单元，用于计算复数的乘法。右侧为两个累加器。

PE-B主要功能用于计算Gram矩阵即矩阵与自身的共轭转置的乘积。计算步骤如下：首先将矩阵H需要相乘的行列输入4片ALU阵列，每个时钟周期可以输入4组数据。经过ALU阵列做乘法。其结果经过累加形成最终结果矩阵G。

如图7是PE-C的结构框图。其中主要包括了：求共轭复数模块。其组成结构也相对简单，由4片求共轭复数模块阵列组成。此处保持PE-A、PE-B相同的4片阵列使计算同步。

PE-C主要功能用于计算矩阵的共轭转置。由左侧输入矩阵H，每个时钟周期可以输入4组复数，经过Conj模块后得到其共轭复数，最终合成矩阵H的共轭转置矩阵。

可以理解的是，根据算法的计算步骤，电路结构被分为3个模块。下面对每一个模块的功能及结构详细说明。

1.初始模块

初始模块拥有两个主要的改进，其一是对一系列迭代参数的新算法，另一个是用户级流水线处理机制。

对于第一个改进而言，α，β，ρ^(k)，可以通过MIMO系统的性质得出，而计算这些参数由于只需要知道B和U，从而计算过程得到了简化。为了提高系统的吞吐率，冗余的数据可以预先被存储在寄存器中，因此这些计算可以被寄存器中的直接数据转化，这些寄存器有效地减少了计算时间和硬件资源。

第二个改进，在用户级流水线处理结构主要用来处理计算y^MF时大规模的乘法。如果每列H^H的向量y都被计算出来，并且每次计算都需要使用。为了减少对寄存器的访问次数，可以将向量y做成流水线结构，如图8所示。该过程一共有U个处理单元，能够实现对下一级、输入数据、八个单元和时钟周期读取的很好的匹配，对输入数据的安排可以很好地使整个系统并行。此外H^H和H由于交替地一次又一次被使用，于是被存储在寄存器中。

2.迭代模块

迭代模块由预迭代模块和迭代模块两部分组成。用户级流水线处理结构同样运用于迭代模块中。每个时钟周期中初始值被传送到预迭代模块中，预迭代模块被做成数组结构来实现用户级流水线，如图9所示。

模块中有8*(U-1)个推进单元PE-B。PE-B中的ALU与PE-A中的不同，因为中心数据被一个个算出。由于初始模块的作用，矩阵H、初始解N₀等数据都可以从寄存器中直接读出。输出、矩阵中的元素被传送到了迭代模块。该模块的输入和评估信号可以被及时使用，从而减少了对存储单元和计算时间的小号。

迭代模块在预迭代模块后，该模块被用来计算迭代k次的残余向量r^(k)和评估信号两个输入的范围和初始模块中用户级流水线结构范围一样，因此迭代模块可以同样被做成用户级流水线结构，这种就够能满足流水线结构的时间约束，减少资源消耗。

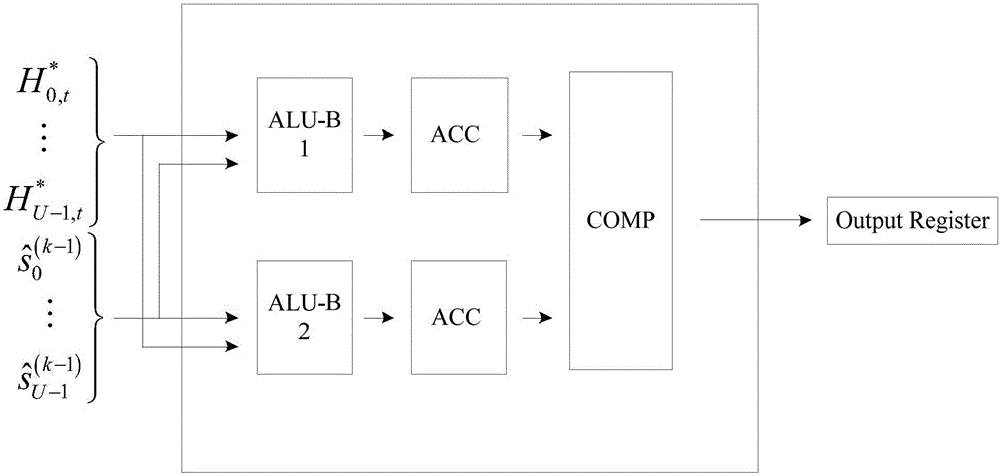
3.最大对数似然比LLR计算模块

这个模块用来计算每一个传输位的最大对数似然比的值。对格雷映射可以被重新改写为分段线性函数。如图10表示了LLR模块的示意图。

处理元素参数β和N₀的输入可以在ALU-B中相乘，同时乘法的倒数也可以通过查表得到。为了减少资源的使用量，每个线性函数的系数被存储在修正的LUT中，最终的软输出可以在ALU-C中计算出。这个最大对数似然比LLR计算模块和之前的方案比大大简化了计算，提高了运行速度，减少了面积和功耗。

根据本发明实施例的大规模MIMO系统中信号检测装置，考虑到信道矩阵的渐进正交性，并且利用特征值产生切比雪夫迭代算法的初值，利用了近似计算规避大规模矩阵转置、相乘带来的计算量，以及根据大规模多入多出系统的属性，提高了收敛速度，实现了大规模多输入多输出无线通信系统中的算法，充分利用了数据并行性计算，实现了高速低功耗的检测译码，提高了检测效率。

其次参照附图描述根据本发明实施例提出的大规模MIMO系统中信号检测方法。

图11是本发明一个实施例的大规模MIMO系统中信号检测方法的流程图。

如图11所示，该大规模MIMO系统中信号检测方法包括以下步骤：

在步骤S1中，获取平稳瑞利分布信道矩阵H、基站段接收信号向量y与噪声的功率密度N₀，以基于信道矩阵的渐进正交性并参照特征值得到预处理后的迭代参数、切比雪夫迭代算法的初始值与匹配滤波后y^MF。

在步骤S2中，根据所预处理后的迭代参数、切比雪夫迭代算法的初始值与匹配滤波后y^MF依次计算评估传递向量U*B矩阵的值H^H，B*1的残差r^(k)，修正向量σ^(k)，和评估传递向量

在步骤S3中，根据评估传递向量与所述预处理后的迭代参数得到最大对数似然比，以得到用户设备发送的原始数据。

进一步地，在本发明的一个实施例中，基站天线数为B，由B行S列的信道矩阵H表示无线通信信道，其中，H中的元素符合平坦瑞利衰落分布。

进一步地，在本发明的一个实施例中，本发明实施例的方法还包括：计算迭代k次的残余向量r^(k)和评估信号

需要说明的是，前述对大规模MIMO系统中信号检测装置实施例的解释说明也适用于该实施例的大规模MIMO系统中信号检测方法，此处不再赘述。

根据本发明实施例的大规模MIMO系统中信号检测方法，考虑到信道矩阵的渐进正交性，并且利用特征值产生切比雪夫迭代算法的初值，利用了近似计算规避大规模矩阵转置、相乘带来的计算量，以及根据大规模多入多出系统的属性，提高了收敛速度，实现了大规模多输入多输出无线通信系统中的算法，充分利用了数据并行性计算，实现了高速低功耗的检测译码，提高了检测效率。

在本发明的描述中，需要理解的是，术语“中心”、“纵向”、“横向”、“长度”、“宽度”、“厚度”、“上”、“下”、“前”、“后”、“左”、“右”、“竖直”、“水平”、“顶”、“底”“内”、“外”、“顺时针”、“逆时针”、“轴向”、“径向”、“周向”等指示的方位或位置关系为基于附图所示的方位或位置关系，仅是为了便于描述本发明和简化描述，而不是指示或暗示所指的装置或元件必须具有特定的方位、以特定的方位构造和操作，因此不能理解为对本发明的限制。

此外，术语“第一”、“第二”仅用于描述目的，而不能理解为指示或暗示相对重要性或者隐含指明所指示的技术特征的数量。由此，限定有“第一”、“第二”的特征可以明示或者隐含地包括至少一个该特征。在本发明的描述中，“多个”的含义是至少两个，例如两个，三个等，除非另有明确具体的限定。

在本发明中，除非另有明确的规定和限定，术语“安装”、“相连”、“连接”、“固定”等术语应做广义理解，例如，可以是固定连接，也可以是可拆卸连接，或成一体；可以是机械连接，也可以是电连接；可以是直接相连，也可以通过中间媒介间接相连，可以是两个元件内部的连通或两个元件的相互作用关系，除非另有明确的限定。对于本领域的普通技术人员而言，可以根据具体情况理解上述术语在本发明中的具体含义。

在本发明中，除非另有明确的规定和限定，第一特征在第二特征“上”或“下”可以是第一和第二特征直接接触，或第一和第二特征通过中间媒介间接接触。而且，第一特征在第二特征“之上”、“上方”和“上面”可是第一特征在第二特征正上方或斜上方，或仅仅表示第一特征水平高度高于第二特征。第一特征在第二特征“之下”、“下方”和“下面”可以是第一特征在第二特征正下方或斜下方，或仅仅表示第一特征水平高度小于第二特征。

在本说明书的描述中，参考术语“一个实施例”、“一些实施例”、“示例”、“具体示例”、或“一些示例”等的描述意指结合该实施例或示例描述的具体特征、结构、材料或者特点包含于本发明的至少一个实施例或示例中。在本说明书中，对上述术语的示意性表述不必须针对的是相同的实施例或示例。而且，描述的具体特征、结构、材料或者特点可以在任一个或第一至第三实施例或示例中以合适的方式结合。此外，在不相互矛盾的情况下，本领域的技术人员可以将本说明书中描述的不同实施例或示例以及不同实施例或示例的特征进行结合和组合。

尽管上面已经示出和描述了本发明的实施例，可以理解的是，上述实施例是示例性的，不能理解为对本发明的限制，本领域的普通技术人员在本发明的范围内可以对上述实施例进行变化、修改、替换和变型。