一种基于改进BPNN的网络安全态势预测方法与流程

本发明涉及网络安全评估技术领域，尤其涉及一种基于改进反向传播神经网络(Back propagation neural network,BPNN)的安全态势预测方法。

背景技术：

近年来，随着移动互联网和智能终端时代的到来与普及，人们的线上行为越来越频繁，营销规模越来越大，各种社交网络组成了复杂、异构的大规模网络。然而，由于通信网络存在可移动性、可扩展性、大规模性、泛在性等特性，在网络深入人们社会生活的同时，也成为黑客攻击的首要目标，导致网络安全漏洞数量持续快速增长。因此，安全问题必将成为未来大规模网络首要解决的问题。在传统技术无法满足人们对大规模网络安全需求的情况下，各国专家学者继而将研究重点转向了网络安全态势感知研究。

网络安全态势预测就是借助过去和现在的黑客攻击行为要素信息，得到对网络未来状态的预测，其本质就是一种根据现在的黑客行为特征推测未来网络安全发展态势的技术方法。一个完整的网络安全态势感知体系包括：在对真实网络的安全要素信息进行提取、理解的前提下，通过对历史和当前数据的观测和分析，进而对网络的未来安全趋势做出推测，辅助网络管理员及时了解网络系统即将发生的攻击行为，并做出及时的防御措施。网络安全态势预测作为态势感知过程的最高层，是网络安全态势感知研究的最终目的。

目前，各国对于网络安全态势感知的研究还处于起步阶段，虽然相关理论和技术都还不太成熟，但研究人员已尝试从不同角度出发研究和提出相关的网络态势预测方法。

Endsley最早给出了态势感知的概念，即从空间和时间两个维度感知环境中 的要素，综合理解感知信息并预测未来的状况。

卓颖等人提出了基于广义回归神经网络的态势预测方法，首先对历史数据进行分类，针对各个类别的数据建立广义神经网络模型，进行态势预测，具有较好的预测精度。

Zhang Guiling等人借助模糊神经网络在处理模糊性、非线性等问题上的优势，提出了基于模糊神经网络的入侵攻击评估模型，用于预测入侵行为。

Liu Z等人从不同角度对网络态势感知开展了研究，提出了采用数据挖掘的方法进行态势感知和预测，但是上述研究存在态势要素提取不全面，计算复杂度过大导致维数爆炸等问题。

谢丽霞等人提出基于神经网络的网络安全态势感知方法，采用遗传算法优化径向基函数(Radical Basis Function,RBF)神经网络，有效提高了预测精度，但在对历史数据集进行相空间重构时，人为指定输入维数缺乏一定的理论依据，具有一定的局限性。

针对上述提出的各种网络安全态势预测方法存在的不足与缺陷，需要寻找一种高效准确地网络安全态势预测方法。

技术实现要素：

本发明的目的是提供一种基于改进BPNN的网络安全态势预测方法，用以解决现有的人为指定输入维数导致网络不可预测以及网络容易陷入局部最优导致网络安全态势预测精度低的问题。

本发明为解决上述技术问题，提供一种基于改进BPNN的网络安全态势预测方法，该方法包括以下步骤：

步骤1，对采集的漏洞、流量、入侵检测系统等数据进行态势要素获取，并通过层次化网络安全态势评估量化方法对收集到的态势要素信息进行评估量化处理；

步骤2，运用极值化公式对量化后产生的非线性时间序列态势值进行预处理，再寻找最适合的嵌入维数与延迟时间进行相空间重构，并通过计算该非线 性的时间序列的李雅普诺夫(Lyapunov)指数来确定是否有可预测性；

步骤3，将空间重构得到的态势值样本分为训练集与测试集；

步骤4，根据非线性时间序列的特点与经验确定BP神经网络的输出层与隐含层的节点数，设定输入层节点数为嵌入维数，从而确定神经网络的结构，并初始化BP神经网络的向量参数Θ；

步骤5，采用改进萤火虫算法(Improved glowworm swarm optimization，IGSO)对BP神经网络进行参数寻优，从而确定网络权值和偏置值，建立网络安全态势的预测模型；

步骤6，将测试集输入至有最优权值和阈值的BPNN中，得到预测值，最后再将其反极值化，得到最终的态势值。

优选地，所述步骤2进一步包括以下步骤：

步骤21，建模极值标准化公式如下所示：

其中，x(i)与x'(i)分别为处理前后的网络安全态势值，x(i)_min与x(i)_max分别表示处理前所有网络安全态势值中的最小值与最大值，且通过处理后得到的网络安全态势数据x'(i),i＝1,2,…n.是一组一维时间序列,其中n为一段时间内的网络安全态势样本数；

步骤22，采用最小互信息法计算最佳时间延时τ，并将τ和cao氏法相结合确定嵌入维数，从而得出BP网络的输入节点数m；

步骤23，根据cao氏法与互信息法得到的m与τ，引入最大Lyapunov指数来验证数据具有可预测性。

优选地，所述步骤22中的最佳时间延时τ的计算公式为：

其中，定义事件a表示网络安全态势样本序列x'(t_i)，事件b表示进行时间延迟 的网络安全态势样本序列x'(t_i+τ)，p_a(x'(t_i))与p_b(x'(t_i+τ))分别表示a、b两事件中x'(t_i)与x'(t_i+τ)会发生的概率，P_ab(x'(t_i),x'(t_i+τ))为x'(t_i)和x'(t_i+τ)两事件联合分布概率；通过对该公式分析可知，如果I(τ)等于0，则代表x'(t_i)与x'(t_i+τ)无相关，即x'(t_i+τ)是不可以预测的；若I(τ)取得极小值，表示x'(t_i)与x'(t_i+τ)具有最大可能的不相关，因此取I(τ)的第一个极小值为最佳时间延迟τ。

优选地，所述步骤22中的根据cao氏法确定输入神经元数m的计算公式为：

E₁(m)＝E(m+1)/E(m)

m代表嵌入维数，也即神经网络的输入节点数，就是通过这几个公式来确定，m从1开始取，一直到E₁(m)停止变化；

其中，X_i(m)和X_i(m+1)分别表示嵌入维为m和m+1时重构相空间的第i个向量，X_n(i,m)(m)和X_n(i,m)(m+1)分别表示与X_i(m)和X_i(m+1)最近的向量，||·||为欧几里得距离，则a(i,m)用于判断X_n(i,m)(m)是否为X_i(m)的真实临近点，若在m维相空间临近的两个点在m+1维相空间依然临近，则为“真实临近点”，否则为“虚假临近点”；E(m)和E(m+1)分别表示在m维和m+1维下非线性时间序列上点与其相邻点之间的平均统计距离，N表示态势值时间序列；进一步，通过对上述公式分析可知，如果网络安全态势的非线性时间序列当中包含确切的规律，那么就一定能够找到一个合适m，当m大于某固定值m₀时，E₁(m)开始停止较大变化则可将m₀+1当作最小嵌入维数，其中判断是否停止较大变化，可以设置一个在0到1范围内波动的E₂(m)，来对比E₁(m)是否大幅增加还是已经停止较大变化，E₂(m)设置准则如下：

E₂(m)＝E^*(m+1)/E^*(m)

对于随机事件序列，数据内部无关联，因此是不可预测的，E₂(m)将始终为1，而对于确定性时间序列，相邻点之间的关系会随着嵌入维数m的值变化，因此总有一些m使得E₂(m)不等于1，因此，E₂(m)的波动程度能够用来度量时间序列中的确定性元素。

优选地，所述步骤2的相空间重构方法为：

其中，m和τ根据步骤22得出，x'(i)为极值化后的一维时间序列，M表示重构相点的数量，m为嵌入维数，即输入层节点数，τ为延迟时间。

优选地，所述步骤5进一步包括以下步骤：

步骤51，将萤火虫群的个体位置映射为BP神经网络的向量参数Θ，并指定种群内萤火虫个体的数目，对所有的个体进行随机实数编码，使得萤火虫种群均匀分布在D维的搜索空间里；

步骤52，初始化IGSO算法的参数，其中包括：最大迭代次数t_max、最小移动步长s_min、最大移动步长s_max、萤火素更新参数ρ、适应度函数参数γ、萤火素初始值l₀、萤火虫感知范围r_s；

步骤53，按照IGSO算法进行迭代寻优，得到萤火虫种群在搜索空间中的全局最优解，即得到BPNN对网络安全态势训练样本预测精度最高的一组向量参数Θ，并基于该组向量参数Θ来构建BP网络中各层之间的连接权值与各节点之间的阈值，进而得到网络安全态势值泛化能力最强的BPNN网络模型。

进一步，所述步骤53中IGSO算法具体步骤为：

步骤531，参数及种群初始化，即设定种群个体数目并在解空间中随机初始化个体位置，计算初始化种群每个个体的适应度函数值，同时生成公告板；

步骤532，对种群中的所有萤火虫个体按l_i(t)＝(1-ρ)l_i(t-1)+γJ(x_i(t))更新萤火素值，其中，l_i(t)表示第t次迭代中第i个萤火虫所携带的萤火素，ρ∈(0,1)为萤火素更新参数，γ为适应度函数参数，J(x)为适应度函数；

步骤533，进入迭代阶段，求解种群中个体的邻居萤火虫的集合，如果邻居集合存在则转到步骤534，否则转到步骤536；

步骤534，根据轮盘赌的方法计算萤火虫i在其决策域内的移动方向，同时为了摆脱陷入局部最优，引入变步长来代替固定步长进行移动步长的更新，并设定变步长公式为：其中，t_max为最大迭代次数，s_min为最小移动步长，s_max为最大移动步长；

步骤535，根据534的步长s(t)进行位置更新,则萤火虫在t+1次迭代的位置x_i(t+1)的更新公式为：

其中，x_i(t)表示萤火虫i在第t次迭代的位置，x_j(t)表示萤火虫i在第t次迭代时决策域内的第j只萤火虫的位置，同时更新萤火虫个体的决策域，设定第i只萤火虫在t+1次迭代时刻的动态决策范围为：

其中，r_s为萤火虫感知范围，为第i只萤火虫t次迭代时刻的动态决策范围，β为比例常数，n_t为邻居阈值；表示第i只萤火虫在第t次迭代时，它的决策域内所包含的萤火虫的集合，l_i(t)表示第t次迭代中第i个萤火虫所携带的萤火素，l_j(t)表示第t次迭代中第j个萤火虫所携带的萤火素，其中，j∈N_i(t)，||x||表示x的范数；

步骤536，计算当前种群所有个体对应的适应度函数值，取其中最好的适应度函数值与公告板中的值进行对比，若优于公告板信息，则选择更新公告板；

步骤537，根据条件判断，如果发生变异即当迭代次数大于2且公告板中连续3代的最优适应度函数值变化都小于u，则执行步骤538，若不发生变异执行步骤539；

步骤538，执行自适应t分布变异，具体为：在萤火虫算法中引入自适应t分布变异操作，利用目前为止所有迭代次数中最优适应度函数值所属萤火虫个体的状态替换当前种群中最差萤火虫个体的状态，然后对本次迭代种群中的最优个体进行高斯变异，对其他的个体按式进行t分布变异，其中，是变异后个体的位置，k是1到0之间递减的变量，t(t_max)是以t_max为参数自由度的学生分布，t_max为最大迭代次数，进而计算所有个体变异后的适应度函数值，若优于公告板信息，则更新公告板；

步骤539，完成一次迭代，判断迭代次数是否达到t_max，若满足则退出迭代，输出公告板上最优的适应度函数值；若不满足执行步骤533，进行下一次迭代。

优选地，所述步骤532中的适应度函数为：

ε(t,X)＝y(t)-y_N(t,Θ)

其中，y(t)为期望输出，y_N(t,Θ)为实际输出，N代表训练集的样本数。

与现有技术相比，本发明达到的有益效果是：

本发明提供了一种改进BPNN的网络安全态势预测方法，通过采集网络和主机的异常信息，过滤网络安全威胁报警事件，从而建立预测模型的训练样本集；使用混沌理论和BP神经网络相结合的方法建立网络安全态势预测模型，通过对样本数据进行相空间重构，避免了人为设定神经网络输入层节点数的问题，同时分析重构后样本的最大李雅普诺夫指数来得到评估出来的样本是具有混沌预测性；考虑到神经网络易陷入局部最优，因此用改进的萤火虫算法对其进行优化；进而本发明能够较为精确的对网络安全进行预测，同时能够提高网络安全态势预测收敛速度。

附图说明

图1是本发明提供的基于改进BPNN的网络安全态势预测方法的流程图；

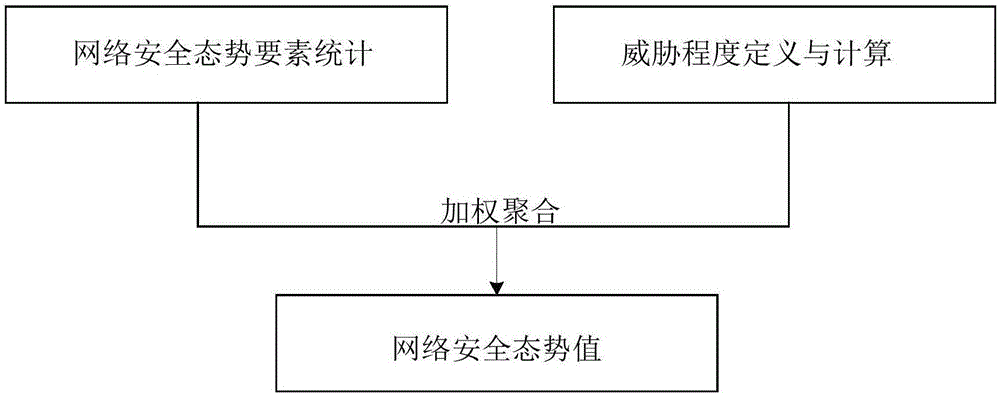
图2是本发明中网络安全态势要素评估量化模型简化图；

图3是本发明中神经网络输入维数m的仿真图；

图4是本发明与BPNN、GSO-BPNN的仿真比较图；

图5是本发明与其他智能优化算法的仿真比较图。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，下面结合附图对本发明的具体实施方式作进一步说明。

本发明所提的基于改进BPNN的网络安全态势预测方法，通过对历史时刻的网络安全态势值进行相空间重构，得出训练集和测试集，同时用改进萤火虫算法优化反向传播神经网络，最后使用训练好的反向传播神经网络进行下一时刻的网络安全态势值预测，图1为本发明提供的基于改进BPNN的网络安全态势预测方法的流程图，该方法包括以下步骤：

步骤1，对采集的漏洞、流量、入侵检测系统等数据进行态势要素获取，并通过层次化网络安全态势评估量化方法对收集到的态势要素信息进行评估量化处理；

步骤2，运用极值化公式对量化后产生的非线性时间序列态势值进行预处理，再寻找最适合的嵌入维数与延迟时间进行相空间重构，并通过计算该非线性的时间序列的Lyapunov指数来确定是否有可预测性；

步骤3，将空间重构得到的态势值样本分为训练集与测试集；

步骤4，根据非线性时间序列的特点与经验确定BP神经网络的输出层与隐含层的节点数，设定输入层节点数为嵌入维数，从而确定神经网络的结构，并初始化BP神经网络的向量参数Θ；

步骤5，采用改进萤火虫算法IGSO对BP神经网络进行参数寻优，从而确定网络权值和偏置值，建立网络安全态势的预测模型；

步骤6，将测试集输入至有最优权值和阈值的BPNN中，得到预测值，最后再将其反极值化，得到最终的态势值。

根据本发明，所述步骤2进一步包括以下步骤：

步骤21，建模极值标准化公式如下所示：

其中，x(i)与x'(i)分别为处理前后的网络安全态势值，x(i)_min与x(i)_max分别表示处理前所有网络安全态势值中的最小值与最大值，通过处理后得到的网络安全态势数据x'(i),i＝1,2,…n.是一组一维时间序列，n为一段时间内的网络安全态势样本数；

步骤22，采用最小互信息法计算最佳时间延时τ，结合τ和cao氏法确定嵌入维数，从而得出BP网络的输入节点数m；

其中，建模最佳时间延时τ的计算公式为：

其中，定义事件a表示网络安全态势样本序列x'(t_i)，事件b表示进行时间延迟的网络安全态势样本序列x'(t_i+τ)，p_a(x'(t_i))与p_b(x'(t_i+τ))分别表示a、b两事件中x'(t_i)与x'(t_i+τ)会发生的概率，P_ab(x'(t_i),x'(t_i+τ))为x'(t_i)和x'(t_i+τ)两事件联合分布概率；通过对该公式分析可知，如果I(τ)等于0，则代表x'(t_i)与x'(t_i+τ)无相关，即x'(t_i+τ)是不可以预测的；若I(τ)取得极小值，表示x'(t_i)与x'(t_i+τ)具有最大可能的不相关，因此取I(τ)的第一个极小值为最佳时间延迟τ；

所述cao氏法可以参见许小可等人论文《基于非线性分析的海杂波处理与目标检测》，大连海事大学，2008，不再详述。

进一步，所述步骤22中利用cao氏法确定输入神经元数m的计算公式为：

E₁(m)＝E(m+1)/E(m)

其中，X_i(m)和X_i(m+1)分别表示嵌入维为m和m+1时重构相空间的第i个向量，X_n(i,m)(m)和X_n(i,m)(m+1)分别表示与X_i(m)和X_i(m+1)最近的向量，||·||为欧几里得距离，则a(i,m)用于判断X_n(i,m)(m)是否为X_i(m)的真实临近点，若在m维相空间临近的两个点在m₊1维相空间依然临近，则为“真实临近点”，否则为“虚假临近点”；E(m)和E(m+1)分别表示在m维和m+1维下非线性时间序列上点与其相邻点之间的平均统计距离，N表示态势值时间序列；进一步，通过对上述公式分析可知，如果网络安全态势的非线性时间序列当中包含确切的规律，那么就一定能够找到一个合适m，当m大于某固定值m₀时，E₁(m)开始停止较大变化则可将m₀+1当作最小嵌入维数，其中判断是否停止较大变化，可以设置一个在0到1范围内波动的E₂(m)，来对比E₁(m)是否大幅增加还是已经停止较大变化，E₂(m)设置准则如下：

E₂(m)＝E^*(m+1)/E^*(m)

对于随机事件序列，数据内部无关联，因此是不可预测的，E₂(m)将始终为1，而对于确定性时间序列，相邻点之间的关系会随着嵌入维数m的值变化，因此总有一些m使得E₂(m)不等于1，因此，E₂(m)的波动程度能够用来度量时间序列中的确定性元素；

步骤23，根据cao氏法与互信息法得到的m与τ，引入最大Lyapunov指数来验证数据具有可预测性。

根据本发明，所述步骤5具体包括以下步骤：

步骤51，将萤火虫群的个体位置映射为BP神经网络的向量参数Θ，并指定种群内萤火虫个体的数目，对所有的个体进行随机实数编码，使得萤火虫种 群均匀分布在D维的搜索空间里；

步骤52，初始化IGSO算法的参数，其中包括：最大迭代次数t_max、最小移动步长s_min、最大移动步长s_max、萤火素更新参数ρ、适应度函数参数γ、萤火素初始值l₀、萤火虫感知范围r_s；

步骤53，按照IGSO算法进行迭代寻优，得到萤火虫种群在搜索空间中的全局最优解，即得到BPNN对网络安全态势训练样本预测精度最高的一组向量参数Θ，并基于该组向量参数Θ来构建BP网络中各层之间的连接权值与各节点之间的阈值，进而得到网络安全态势值泛化能力最强的BPNN网络模型。

根据本发明，所述步骤51进一步包括以下步骤：

步骤511，在解空间中，将具体的萤火虫个体编码为：

Θ＝[w,v,θ,α]

其中，w为隐含层各节点与输入层各节点之间的连接权值，v为隐含层各节点与输出层各节点之间的连接权值，θ为隐含层节点的偏置值，α输出层节点的偏置值；

步骤512，搜索空间维数的确定：设输入层节点的个数为m，隐含层节点的个数为p，输出层节点的个数为1，那么，输入层与隐含层的连接权值维数为m×p；隐含层与输出层之间的连接权值维数为p；隐含层节点对应的阈值维数为p；输出层节点对应的阈值维数为1；则算法中萤火虫个体的搜索空间维数为：

D＝(m×p+p)+(p+1)

由上式可知，每个萤火虫个体在空间当中都具有D个维度，则萤火虫个体编码可以表示为：Θ＝[x₁,x₂,…,x_D]，当搜索到最优的Θ时，该位置的目标函数适应度最大。

进一步，所述步骤53中IGSO算法具体包括以下步骤：

步骤531，设定种群个体数目并在解空间中随机初始化个体位置，计算初始化种群每个个体的适应度函数值，同时生成公告板；

步骤532，对种群中的所有萤火虫个体按l_i(t)＝(1-ρ)l_i(t-1)+γJ(x_i(t))更新萤火素值，其中，l_i(t)和l_i(t-1)分别表示第t次和第t-1次迭代中第i个萤火虫所携带的萤火素，ρ∈(0,1)为萤火素更新参数，γ为适应度函数参数，J(x)为适应度函数，其具体计算公式为：

ε(t,X)＝y(t)-y_N(t,Θ)

其中，y(t)为神经网络期望输出，y_N(t,Θ)为神经网络实际输出，N为训练集的样本数；

步骤533，进入迭代阶段，求解种群中个体的邻居萤火虫的集合，如果邻居集合存在则转到步骤535，邻居集合不存在就转到步骤536；

步骤534，根据轮盘赌的方法计算萤火虫i在其决策域内的移动方向，同时为了摆脱陷入局部最优，引入变步长来代替固定步长进行移动步长的更新，并设定变步长公式为：

步骤535，根据534的步长s进行位置更新,则萤火虫在t+1次代的位置x_i(t+1)的更新公式为：

其中，x_i(t)表示萤火虫i在第t次迭代的位置，x_j(t)表示萤火虫i在第t次迭代时决策域内的第j只萤火虫的位置，同时更新萤火虫个体的决策域，设定第i只萤火虫在t+1次迭代时刻的动态决策范围为：

其中，r_s为萤火虫感知范围，为第i只萤火虫t次迭代时刻的动态决策范围，β为比例常数，n_t为邻居阈值；表示第i只萤火虫在第t次迭代时，它的决策域内所包含的萤火虫的集合，其中，j∈N_i(t)，||x||表示x的范数；

步骤536，计算当前种群所有个体对应的适应度函数值，取其中最好的适应度函数值与公告板中的值进行对比，若优于公告板信息，则选择更新公告板；

步骤537，根据条件判断，如果发生变异即当迭代次数大于2且公告板中连续3代的最优适应度函数值变化都小于u，则执行步骤538，若不发生变异执行步骤539；

步骤538，执行自适应t分布变异，具体为：在萤火虫算法中引入自适应t分布变异操作，利用目前为止所有迭代次数中最优适应度函数值所属萤火虫个体的状态替换当前种群中最差萤火虫个体的状态，然后对本次迭代种群中的最优个体进行高斯变异，对其他的个体按式进行t分布变异，其中，是变异后个体的位置，k是1到0之间递减的变量，t(t_max)是以t_max为参数自由度的学生分布，进而计算所有个体变异后的适应度函数值，若优于公告板信息，则更新公告板；

步骤539，完成一次迭代，判断迭代次数是否达到t_max，若满足则退出迭代，输出公告板上最优的适应度函数值；若不满足执行步骤533，进行下一次迭代。

为了说明本发明的有益效果，本发明将结合具体的态势值进行仿真分析。取某公司10-11月中60天里防火墙、入侵检测系统(Intrusion Detection Systems,IDS)等历史日志信息作为原始数据源。对每天的日志信息进行5次采样，并将采样得到的日志信息按照图2所示方法进行网络安全评估量化，从而得到原始态势值。实验中IGSO算法的具体参数如表1所示。

表1仿真参数

图3描述了最小嵌入维数m的确定，对归一化后的网络安全态势值进行互信息法得到最佳时间延时τ＝1，再将τ与cao氏法相结合计算出m。从图中可知，从m＝5开始，E₁(m)和E₂(m)差值控制在一定范围内，即E₁(m)不再发生较大变化， 所以确定利用cao氏法求出的最小嵌入维数为5。

图4为本发明提出的IGSO-BPNN算法与通过单纯的BPNN算法和未经改进的萤火虫算法优化BPNN(GSO-BPNN)算法得到的态势预测精度对比图。在实验中，设定IGSO、GSO等算法的种群个体数目均取值为30，相当于同时在空间中30个点上一起并行的进行学习，选取拟合最好的点作为权值和阈值进行预测，则对于BPNN模型而言，进30次仿真，取预测精度最高的一组与其他算法进行对比。通过智能算法与神经网络相结合的组合模型比单纯的神经网络预测算法更加符合真实值的趋势。将IGSO-BPNN与GSO-BPNN预测模型进行对比，可以看出改进后的IGSO算法相比GSO算法在寻优过程中更具有优势，经过IGSO优化后的BPNN神经网络模型精度更高，且IGSO-BPNN模型预测的态势趋势更接近于真实趋势。

图5给出了通过本发明提出的IGSO-BPNN算法、遗传算法以及粒子群算法优化BPNN算法得到的网络安全态势预测效果的对比图。在仿真中，设定网络的最大迭代次数为100次，种群最大数量为30，对20组数据进行预测。通过比较可以看出，以实际值曲线作为衡量准则，本发明所提IGSO-BPNN预测模型相比其它两种优化算法所预测得到的结果，其所预测出的趋势走向更贴近真实态势值的趋势。

本发明所举实施方式或者实施例对本发明的目的、技术方案和优点进行了进一步的详细说明，所应理解的是，以上所举实施方式或者实施例仅为本发明的优选实施方式而已，并不用以限制本发明，凡在本发明的精神和原则之内对本发明所作的任何修改、等同替换、改进等均应包含在本发明的保护范围之内。