一种能量采集绿色认知无线电的频谱感知方法与流程

本发明涉及的是一种认知无线电的频谱感知的方法。
背景技术：
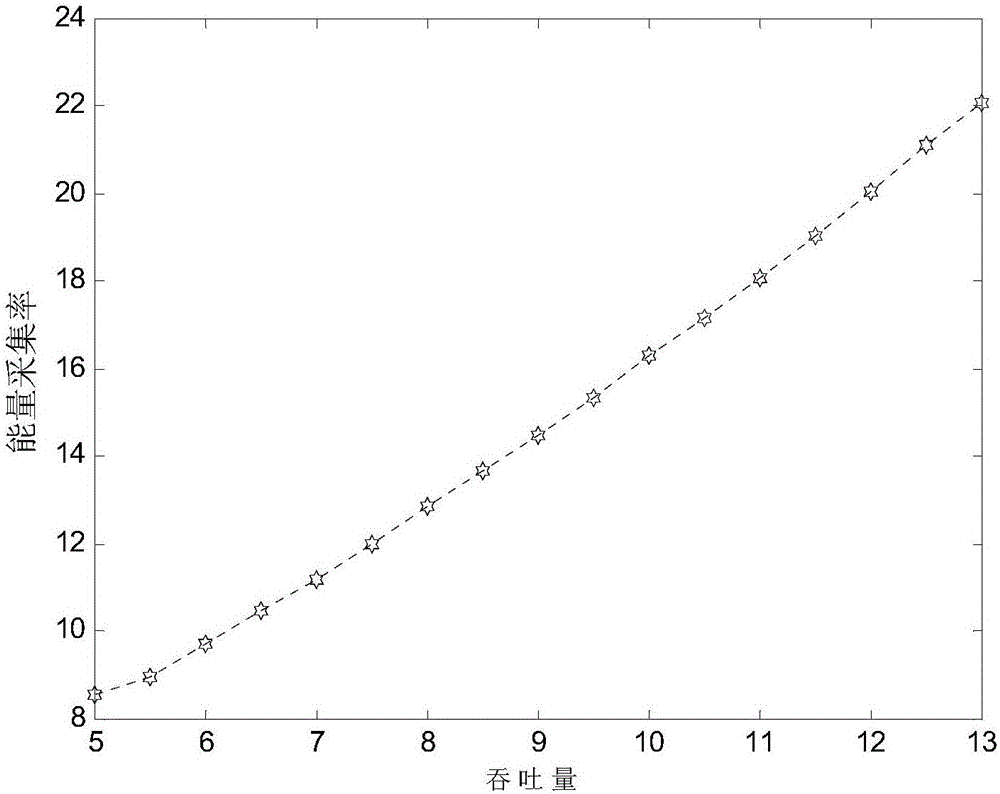
：随着通信事业的迅速发展，频谱资源短缺的问题变得越来越严重。同时随着通信终端多样化、智能化以及宽屏化的发展，移动设备的耗电量也变得越来越不容忽视。如何提高通信系统的频谱利用率同时降低能量消耗是目前急需解决的问题，“绿色通信”的概念也应运而生。相比普通的通信系统，认知无线电系统需要对无线电磁环境进行感知，通过感知功能来寻找可用信道，并自适应的调整系统参数，在不干扰授权用户的前提条件下，最佳的利用频谱空洞来获得最大的数据传输吞吐量，实现认知用户和授权用户共用同一频段，以此来提高无线资源的使用率。近两年，能量采集技术越来越受到重视，因为能量采集技术不仅能极大的缓和能源不足，而且是一种低碳环保技术。无线信号在携带信息的同时也携带了能量，这样环境中的各种干扰信号将会通过能量采集技术变废为宝。因此，能量采集认知无线电的频谱感知技术得到了广泛的关注。郑仕链等在《物理学报》上发表的“基于改进混合蛙跳算法的认知无线电协作频谱感知”提出了改进的混合蛙跳算法的频谱感知方案，没有利用能量采集技术，仅对检测概率进行了研究。YinSixing等在IEEEInternationalConferenceonCommunications会议上发表的“OptimalSaving-Sensing-TransmittingStructureinSelf-PoweredCognitiveRadioSystemswithWirelessEnergyHarvesting”对能量采集的认知无线电频谱感知技术中的次用户吞吐量问题进行了讨论，但是不能求得次用户所需的最小能量采集率，具有改进的余地。技术实现要素：本发明的目的在于提供一种能量需求最小，对能量采集的硬件要求低的能量采集绿色认知无线电的频谱感知方法。本发明的目的是这样实现的：步骤一，建立能量采集绿色认知无线电的频谱感知系统模型；步骤二，初始化种群；步骤三，对所有种群中的所有量子个体的适应度进行评价；步骤四，针对每一个种群，分别对其内部的量子个体进行混合量子差分演化；步骤五，比较每个种群之间的全局最优解，如果全局最优解均相同，对种群内的个体进行灭绝处理；步骤六，如果进化没有终止，返回步骤四，否则执行步骤七；步骤七，终止迭代，输出任意种群的全局最优量子个体的量子态，根据映射规则将其映射为可行解，作为认知无线电频谱感知的方案。本发明还可以包括：1、步骤一具体包括：采用能量采集-频谱感知-数据传输即SST(saving-sensing-transmitting)的时隙结构，所述时隙结构将一个时隙划分为三个时隙片段，分别用于能量采集、频谱感知与数据传输，每个时隙的总时间是T，能量采集因子为ρ，用于能量采集的时间片段长度为ρT，设感知信道数目为q，感知一个信道的时间花销为Ts，用于频谱感知的时间长度为qTs，剩下的时隙片段用于数据传输；将基于SST的时隙结构引入能量采集技术后，若每个时隙次用户需要获得的系统吞吐量为R，其能量采集率X(ρ,q)为：X(ρ,q)=(qEs+(T-ρT-qTs)(2RTM(T-ρT-qTs)-1))/ρT]]>其中Es为探测一个信道所花费的能量，M是可用信道数；信道状态满足参数为p的Bernoulli分布，p为信道空闲的概率，从而M是参数为(q,p)的二项分布随机变量，其期望值为：E[M]＝qp能量采集率最小值优化问题方程如下：X(ρ,q)=(qEs+(T-ρT-qTs)(2RTq(T-ρT-qTs)-1))/ρT]]>约束条件为：ρ-qEs/TX(ρ,q)≥0，1-ρ-qTs/T≥0，0≤ρ≤1其中q∈{0,1,2,…,N}，N表示所能感知信道的最大数目，ρ-qEs/TX(ρ,q)≥0与1-ρ-qTs/T≥0为约束条件，用以确保频谱感知过程既不会消耗完所有的能量也不会消耗完所有的剩余时间；定义如下惩罚函数：其中和是惩罚因子，并且[x]+＝max{x,0}。2、步骤二具体包括：多种群共生进化中有I个种群，每个种群中H个量子个体，第t代第i个种群中第h个量子个体表示为其中表示第t代第i个种群第h个量子个体ρ的量子状态，表示第t代第i个种群第h个量子个体q的量子状态，其中首先是对每一个种群内部进行进化，将第i个种群中的第h个量子个体的分量映射为整数解，而分量保持不变，令映射规则如下：令其中，l是感知信道数目的下界，u是感知信道数目的上界，映射规则为表示对的向下取整函数，映射后的结果为3、对所有种群中的所有量子个体的适应度进行评价步骤中，种群i中的第h个量子个体适应度通过下式进行计算：适应度值越小代表所需要的能量采集率越低，适应度越好，选出每个种群i内适应度最好的量子个体为该种群的全局最优量子个体4、步骤四具体包括：种群i的演化过程如下：(1)变异过程：对第i个种群内的第h个量子个体进行变异操作，其量子旋转角和量子位的更新方程如下：θhnt+1(i)=12·ξ1.(gnt(i)-xhnt(i))+12·ξ2·sign(f(x‾‾at(i))-f(x‾‾ht(i)))·(xant(i)-xhnt(i))+12·ξ3.(gnt(k)-xhnt(i))]]>shnt+1(i)=abs(xhnt(i)·cosμhnt+1(i)+1-(xhnt(i))2·sinμhnt+1(i)),ifϵhnt+1(i)≤0.01)abs(xhnt(i)·cosθhnt+1(i)+1-(xhnt(i))2·sinθhnt+1(i)),otherwise]]>其中，ξ1、ξ2、ξ3和是[0,1]间的均匀随机数，sign(.)表示符号函数，是均值为0方差为1的高斯随机数，a∈{1,2,…,H}是一个随机整数，表示随机选中的量子个体的标号，是种群k(k≠i)的全局最优量子个体，n＝1,2；(2)交叉过程：更新方程如下：vhnt+1(i)=xhnt(i)ifξ4>CRshnt+1(i),else]]>其中ξ4是一个[0,1]间的均匀随机数，CR＝0.01+(0.4t)/K，K是最大迭代次数；(3)选择过程：将量子位置的分量映射为整数解，而分量保持不变，形成新的映射解计算和的适应度，之后对每个种群内部的量子个体和全局最优量子个体进行更新，如果比的适应度好，否则令b为其中适应度最好的量子个体标号，如果的适应度好于否则gt+1(i)＝gt(i)。5、对种群内的个体进行灭绝处理的具体方法是每隔Ka次迭代后，比较每个种群之间的全局最优解，如果全局最优解均相同，则选取一个随机整数w(w∈{1,2,…,I})，种群w内的一半量子个体重新进行初始化生成。本发明提出了一种能量采集绿色认知无线电的频谱感知方法，在系统所需吞吐量已知的条件下，寻求系统的最小能量采集率，通过无线能量传输和采集实现认知无线电系统的自供能，而无需额外的能源供应装置。本发明将能量采集和“绿色通信”等思想应用于认知无线电频谱感知问题，为求解最小的能量采集率，本发明设计了多种群量子混合差分共生进化演进机制，相比于已有的频谱感知方法，本发明具有以下优点：(1)本发明在次户所需吞吐量已知的条件下，设计了多种群量子混合差分共生进化演进机制作为求解最小能量采集效率的方法，所设计的方法性能稳定，可以在短时间内求出最优频谱感知方案。(2)本发明响应“绿色通信”和“低碳通信”等理念，可求出最优能量采集因子和感知信道数目，获得最小能量采集率，可以实现能量需求最小，避免了能量冗余及能量浪费，对能量采集的硬件要求可以达到最低，节省硬件资源，避免造成资源浪费。(3)本发明将量子、混合差分算法和多种群共生进化等思想进行结合，设计了求解混合整数和连续变量问题的多种群量子混合差分共生进化方法，可以为解决其他工程问题提供了新的思路。附图说明图1能量采集绿色认知无线电的频谱感知方法示意图。图2平均最小能量采集率与吞吐量之间的关系。图3最佳能量采集因子与吞吐量之间的关系。图4最佳信道感知数目与吞吐量之间的关系。具体实施方式下面举例对本发明做更详细的描述。结合图1，本发明的能量采集绿色认知无线电的频谱感知方法主要包括如下步骤：步骤一，建立能量采集绿色认知无线电的频谱感知系统模型，本发明提出一种能量采集-频谱感知-数据传输(saving-sensing-transmitting,SST)的时隙结构，该时隙结构将一个时隙划分为三个时隙片段，分别用于能量采集、频谱感知与数据传输。每个时隙的总时间是T，能量采集因子为ρ(度量能量采集时隙片段占总时间的百分数)，则用于能量采集的时间片段长度为ρT。频谱感知时隙片段的长度取决于感知的信道数目，假设感知信道数目为q，感知一个信道的时间花销为Ts，则用于频谱感知的时间长度为qTs。剩下的时隙片段则用于数据传输。将基于SST的时隙结构引入能量采集技术后，若每个时隙次用户需要获得的系统吞吐量为R，其能量采集率X(ρ,q)为：X(ρ,q)=(qEs+(T-ρT-qTs)(2RTM(T-ρT-qTs)-1))/ρT]]>其中q为感知信道数目，Es为探测一个信道所花费的能量，T为每个时隙的总时间，ρ为能量采集因子，Ts为感知一个信道的时间花销，R为每个时隙次用户需要获得的吞吐量，M是可用信道数。信道状态满足参数为p(信道空闲的概率)的Bernoulli分布，从而M是参数为(q,p)的二项分布随机变量，其期望值为：E[M]＝qp因此，次用户所需的能量采集率是一个随机变量。由于本发明的目标是最小化次用户所需能量采集率的长期均值E[X(ρ,q)]，因此本发明的能量采集率最小值优化问题方程如下：X(ρ,q)=(qEs+(T-ρT-qTs)(2RTq(T-ρT-qTs)-1))/ρT]]>约束条件为：ρ-qEs/TX(ρ,q)≥0，1-ρ-qTs/T≥0，0≤ρ≤1其中q∈{0,1,2,…,N}，N表示所能感知信道的最大数目，ρ-qEs/TX(ρ,q)≥0与1-ρ-qTs/T≥0为约束条件，用以确保频谱感知过程既不会消耗完所有的能量也不会消耗完所有的剩余时间。为了将带约束优化问题转换成无约束优化问题，引入惩罚因子的概念，定义如下惩罚函数：其中和是惩罚因子，并且[x]+＝max{x,0}。步骤二，初始化种群，多种群共生进化中有I个种群(对于该问题I＝2)，每个种群中H个量子个体，第t代第i个种群中第h个量子个体表示为其中表示第t代第i个种群第h个量子个体ρ的量子状态，表示第t代第i个种群第h个量子个体q的量子状态，其中首先是对每一个种群内部进行进化，将第i个种群中的第h个量子个体的分量映射为整数解，而分量保持不变，令映射规则如下：首先令其中，l是感知信道数目的下界，u是感知信道数目的上界。因为感知信道数目是一个整数优化问题，要把实数解映射为整数解，映射规则为表示对的向下取整函数，映射后的结果为对所有种群中的所有量子个体的适应度进行评价，种群i中的第h个量子个体适应度通过下式进行计算：适应度值越小代表所需要的能量采集率越低，适应度越好。选出每个种群i内适应度最好的量子个体为该种群的全局最优量子个体步骤三，针对每一个种群，分别对其内部的量子个体进行混合量子差分演化，种群i的演化过程如下：1.变异过程：对第i个种群内的第h个量子个体进行变异操作，其量子旋转角和量子位的更新方程如下：θhnt+1(i)=12·ξ1.(gnt(i)-xhnt(i))+12·ξ2·sign(f(x‾‾at(i))-f(x‾‾ht(i)))·(xant(i)-xhnt(i))+12·ξ3.(gnt(k)-xhnt(i))]]>shnt+1(i)=abs(xhnt(i)·cosμhnt+1(i)+1-(xhnt(i))2·sinμhnt+1(i)),ifϵhnt+1(i)≤0.01)abs(xhnt(i)·cosθhnt+1(i)+1-(xhnt(i))2·sinθhnt+1(i)),otherwise]]>其中，ξ1、ξ2、ξ3和是[0,1]间的均匀随机数，sign(.)表示符号函数，是均值为0方差为1的高斯随机数，a∈{1,2,…,H}是一个随机整数，表示随机选中的量子个体的标号，是种群k(k≠i)的全局最优量子个体，n＝1,2。2.交叉过程：为了增加种群多样性，进行交叉过程，更新方程如下：vhnt+1(i)=xhnt(i)ifξ4>CRshnt+1(i),else]]>其中ξ4是一个[0,1]间的均匀随机数，CR＝0.01+(0.4t)/K，K是最大迭代次数。3.选择过程：将量子位置的分量映射为整数解，而分量保持不变，形成新的映射解计算和的适应度。之后对每个种群内部的量子个体和全局最优量子个体进行更新。如果比的适应度好，否则令b为其中适应度最好的量子个体标号，如果的适应度好于否则gt+1(i)＝gt(i)。步骤四，每隔Ka次迭代后，比较每个种群之间的全局最优解，如果全局最优解均相同，要对某些种群内的某些个体进行灭绝处理，具体方法是选取一个随机整数w(w∈{1,2,…,I})，种群w内的一半量子个体重新进行初始化生成。步骤五，如果进化没有终止(通常由预先设定的最大迭代次数K决定)，返回步骤三，否则，终止迭代，输出任意种群的全局最优量子个体的量子态，根据映射规则将其映射为可行解，作为认知无线电频谱感知的方案。仿真中假设认知无线电的频谱感知模型中，N＝10，T＝1，Ts＝0.03，种群数I＝2，每个种群规模和终止迭代次数都设置为相同，群体规模为H＝50，Ka＝K/5，最大迭代次数K＝1000，Es＝0.6，惩罚因子次用户所期望的吞吐量从5变化到13。图2描绘了在次用户所需不同吞吐量的情况下，基于能量采集的绿色认知无线电频谱分配系统的最小能量采集率，可以看出最小能量采集率与吞吐量之间是一种近似线性关系，表明采集的能量通过提出的分配机制被充分利用了。图3和图4为次用户所需不同吞吐量的情况下，最佳能量采集因子和最佳频谱感知信道数，可以看出，随着吞吐量需求的增大，频谱感知系统更倾向于更高的能量采集因子和更多的频谱感知信道数目。以上内容是结合具体的实施方式对本发明所作的进一步详细说明，不能认定本发明的具体实施只局限于这些说明。对于本发明所属
技术领域：
的普通技术人员来说，在不脱离本发明构思的前提下，还可以做出若干简单推演或替换，都应当视为属于本发明的保护范围。当前第1页1 2 3