一种记忆分布式最小二乘方法与流程

本发明涉及感知网络、分布式估计，d-LMS等领域，尤其涉及一种记忆分布式最小二乘(记忆d-LMS)方法。

背景技术：

无线传感网络由大量感知节点构成，经部署后可以监控难以达到的区域，如深海、森林火灾、大气污染等等。分布在几何区域的节点将收集该区域的数据，为了分析数据中的参数，设计和分析网络的估计算法十分重要。一般来说，分析算法有两种，集中式估计和分布式估计。在集中式估计算法中，所有节点将它们的测量结果传输到中央融合中心来处理，最终分析结果会被送回到这些节点。这种方法可以获得全局解，但是它需要消耗大量的能量。而且，如果融合中心产生问题的话，结果会变得不可靠。在分布式估计算法中，每一个节点都只与它的邻近节点互相传递信息，信息的处理也只在本地进行。与集中式估计相比，分布式估计能够获得更好的估计而且减少了算法复杂度。为了更有效的利用节点获得的历史统计信息，我们提出了一种分布估计方法，称为记忆分布式最小二乘(记忆d-LMS)算法。

技术实现要素：

本发明的目的是针对现有技术不足，提出一种记忆d-LMS，它是在d-LMS的基础上，通过增加额外的统计信息而得来的，具体的是一种记忆分布式最小二乘方法。

本发明解决其技术问题所采用的技术方案包括如下步骤：

步骤1：初始化：对于任意一个节点l，其网络中待估计参数ω的初始估计值ω_l,0为0。

步骤2：在时刻i，网络中每个节点l获取测量信息{x_l,j,y_l,j}；其中，x_l,j为节点l在时刻j的M×1维的已知输入信息，y_l,j表示1×1的观察信息，x_l,j和y_l,j满足如下线性关系：

y_l,j＝x_l,jω+e_l,j； 公式(1)

ω为未知待估参数，e_l,j表示零均值、方差为的独立同分布的随机误差；

步骤3：在时刻i，每个节点l计算从时刻i-i₀+1到时刻i的互相关函数之和α_l,i与自相关函数之和β_l,i，得到：

其中，x_l,j^T表示x_l,j的转置，i₀表示一个取值范围在1与i之间的正整数；

步骤4：每个节点将其在步骤3中的计算结果传输到邻近节点，任意节点k根据如下公式得到未知待估参数ω的预估计，记为

其中，ω_k,i-1表示节点k在时刻i-1的估计值，μ_k表示迭代步长，{c_l,k}表示节点l和节点k的非负权系数集合，满足：

当节点l和节点k没有连接时c_l,k＝0。

步骤5：每个节点k将步骤4中其邻近节点的预估计值结合起来获得估计结果ω_k,i：

其中，{a_l,k}表示节点l和节点k的非负权系数集合，满足

1^TA＝1^T 公式(6)

其中A＝{a_l,k}_N×N，且当时，a_l,k＝0。

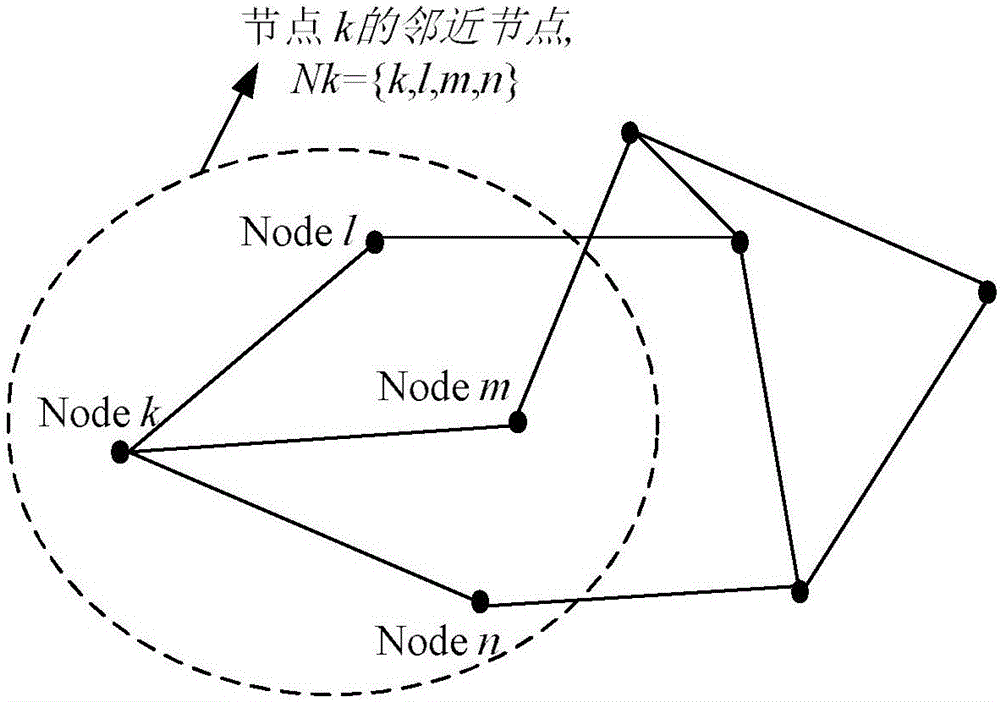
其中，N_k表示节点k的邻近节点的集合，所述的邻近节点包括相连的相邻节点和自身节点。

本发明中步骤1是初始化步骤，初始化完成以后，重复进行步骤2、步骤3、步骤4和步骤5，直到估计值收敛。

本发明有益效果如下：

本发明与传统算法相比，本算法充分利用了各个节点的历史测量信息，使得估计值更接近于真实值，收敛速度更快，均方误差更小。

附图说明

图1为本发明一个实施例。

具体实施方式

下面结合附图和实施例，对本发明作进一步说明。

一种记忆分布式最小二乘方法，具体步骤如下：

步骤1：初始化：对于所有的节点l，网络中待估计参数ω的初始估计值ω_l,0为0。

步骤2：在时刻i，网络中每个节点l获取测量信息{x_l,j,y_l,j}；其中，x_l,j为节点l在时刻j的M×1维的已知输入信息，y_l,j表示1×1的观察信息，x_l,j和y_l,j满足如下线性关系：

y_l,j＝x_l,jω+e_l,j； 公式(1)

ω为未知待估参数，e_l,j表示零均值、方差为的独立同分布的随机误差；

步骤3：在时刻i，每个节点l计算从时刻i-i₀+1到时刻i的互相关函数之和α_l,i与自相关函数之和β_l,i，得到：

其中，x_l,j^T表示x_l,j的转置，i₀表示一个取值范围在1与i之间的正整数；

步骤4：每个节点将其在步骤3中的计算结果传输到邻近节点，任意节点k根据如下公式得到ω的预估计，记为

其中，ω_k,i-1表示节点k在时刻i-1的估计值，μ_k表示迭代步长，{c_l,k}表示节点l和节点k的非负权系数集合，满足：

当节点l和节点k没有连接时c_l,k＝0。

步骤5：每一个节点k将步骤4中其邻近节点的预估计值结合起来获得估计结果ω_k,i：

其中，{a_l,k}表示节点l和节点k的非负权系数集合，满足

1^TA＝1^T 公式(6)

其中A＝{a_l,k}_N×N，且当时，a_l,k＝0。

其中，N_k表示节点k的邻近节点的集合，所述的邻近节点包括相连的相邻节点及其本身。

说明：步骤1完成以后，重复进行步骤2、步骤3、步骤4和步骤5，直到估计值收敛。

其中，N_k表示节点k的邻近节点的集合，所述的邻近节点包括相连的相邻节点及其本身。

说明：步骤1和步骤2完成以后，重复进行步骤3、步骤4和步骤5，直到估计值收敛。

实施例1：

下面参照附图并结合本发明的优选实施例来描述本发明的一种记忆分布式最小二乘方法(记忆d-LMS)。具体的为分布式感知网络的拓扑结构图，图中黑色实心圆点表示网络节点，节点之间的连线表示节点之间可以互相传递信息，没有连线的节点之间则不能传递信息。图中节点k的邻近节点是节点k，节点l，节点m和节点n。