扬声器振膜状态估计方法及应用其的扬声器驱动电路与流程

本发明涉及声学领域，具体涉及一种扬声器振膜状态估计方法及应用其的扬声器驱动电路。

背景技术：

扬声器基于电磁线圈产生电磁场驱动振膜振动发声。扬声器的额定功率受到其最大振膜偏移量的限制。如果振膜偏移量超过其最大安全偏移量，则可能会导致扬声器不可恢复的损坏。某些特殊情况下，可以使扬声器的输出功率大于额定功率，同时振膜偏移小于最大安全偏移量，从而在保证器件安全的前提下输出大于额定功率的声音，提高扬声器的利用率。特别是在便携式设备中，对扬声器体积要求较高，扬声器的额定功率受限，能够产生的最大声压也受到限制，因此，对保证扬声器振膜在安全工作范围内，同时扩大其输出功率，增大输出声压的需求越来越高。

为了实现上述目的，需要准确估计扬声器振膜的位移，传统的检测振膜位移的方法有采用激光测位移和激光测速或者声压检测等方法，然而这些方法均需要使用传感器，使得扬声器系统装置的体积大，不易安装，难以实现，且成本高，因此这些方法通常只能用于科学实验，很难应用到实际产品中。

技术实现要素：

有鉴于此，本发明提供一种扬声器振膜状态估计方法及应用其的扬声器驱动电路，以快速、准确地估计扬声器振膜状态，从而为实现对于扬声器的精确控制提供支持。

第一方面，提供一种扬声器振膜状态估计方法，包括：

通过自适应滤波方法调整振膜位移模型的权重值，直至使得扬声器驱动电压估计值与扬声器的驱动电压测量值的误差小于预定阈值；

根据最终确定的权重值对应的振膜位移模型估计扬声器的振膜相对位移；

其中，所述振膜位移模型根据当前时刻输入电流、当前时刻振膜相对速度估计值和当前时刻振膜相对位移估计值组成的向量与权重值向量的乘积计算下一时刻的振膜相对速度，并根据当前时刻振膜速度估计值、当前时刻输入电流和扬声器直流阻抗计算所述驱动电压估计值。

优选地，所述通过自适应滤波方法调整振膜位移模型的权重值包括：

根据当前权重值对应的振膜位移模型计算下一时刻的振膜相对速度和振膜相对位移，并计算当前时刻的驱动电压估计值；

根据当前时刻的扬声器驱动电压估计值和驱动电压测量值计算误差；

在所述误差大于预定阈值时，基于自适应滤波方法根据扬声器参数的历史数据更新所述权重值。

优选地，所述振膜位移模型为：

其中，R为所述扬声器直流阻抗，i(k)为时刻k的输入电流，v(k)为时刻k的振膜速度，u(k)为时刻k的驱动电压估计值，s(k)为振膜相对位移，a，b，c分别为i(k)、v(k)和s(k)对应的权重值。

优选地，所述自适应滤波方法为最小均方算法(LMS)。

优选地，所述扬声器直流阻抗通过估计获得。

优选地，所述方法还包括：

根据振膜相对位移与振膜绝对位移的预定关系以及计算获得的振膜相对位移获取振膜绝对位移。

优选地，所述振膜相对位移与振膜绝对位移的预定关系为预先测定的比例系数。

第二方面，一种扬声器驱动电路，包括处理器，所述处理器适于执行如上所述的方法。

通过将输入电流、估计得到的扬声器振膜相对速度和相对位移作为输入，将扬声器的驱动电压作为输出，将非线性的电机耦合系数标幺化为1获得更为简化的扬声器振膜位移模型，基于自适应滤波方法调整振膜位移模型的权重值，直至使得驱动电压估计值与驱动电压测量值的误差小于预定阈值，并根据最终确定的额权重值来对振膜相对位移进行估计，从而可以快速、准确地估计扬声器振膜位移，实现对于扬声器的精确控制。

附图说明

通过以下参照附图对本发明实施例的描述，本发明的上述以及其它目的、特征和优点将更为清楚，在附图中：

图1是本发明实施例的扬声器振膜状态估计方法的流程图；

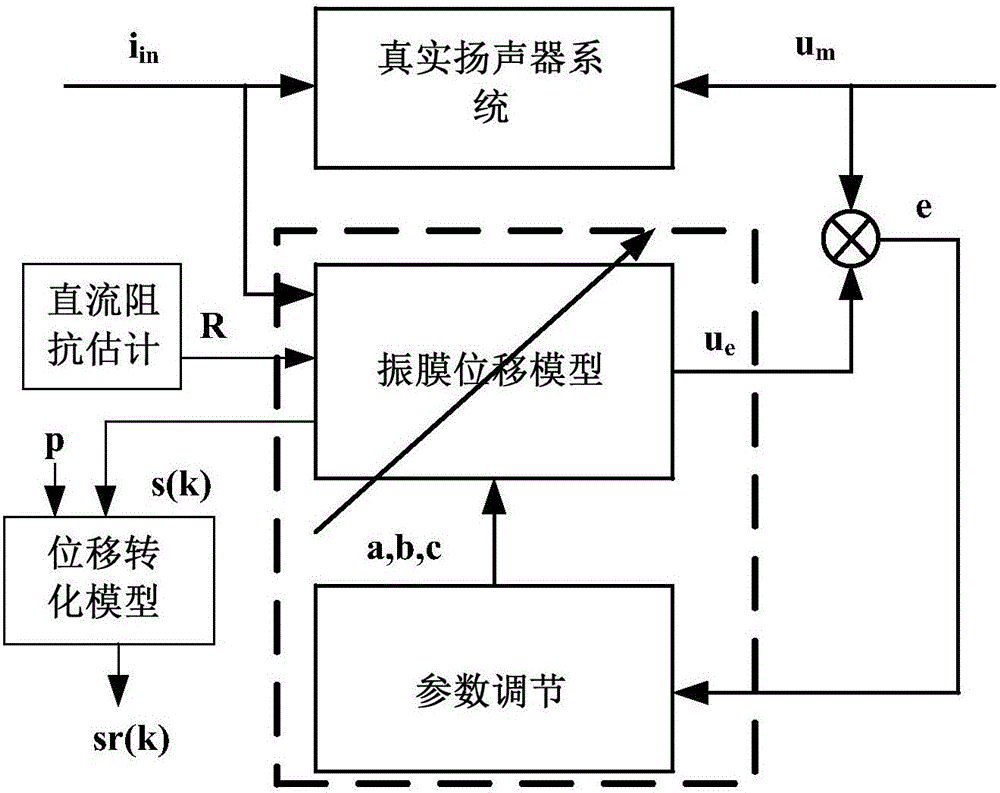
图2是本发明实施例的扬声器振膜状态估计方法的数据流图；

图3为扬声器的电磁和机械振动模型的示意图；

图4是本发明实施例中进行权重值调整的流程图。

具体实施方式

以下基于实施例对本发明进行描述，但是本发明并不仅仅限于这些实施例。在下文对本发明的细节描述中，详尽描述了一些特定的细节部分。对本领域技术人员来说没有这些细节部分的描述也可以完全理解本发明。为了避免混淆本发明的实质，公知的方法、过程、流程、元件和电路并没有详细叙述。

此外，本领域普通技术人员应当理解，在此提供的附图都是为了说明的目的，并且附图不一定是按比例绘制的。

除非上下文明确要求，否则整个说明书和权利要求书中的“包括”、“包含”等类似词语应当解释为包含的含义而不是排他或穷举的含义；也就是说，是“包括但不限于”的含义。

图1是本发明实施例的扬声器振膜状态估计方法的流程图；图2是本发明实施例的扬声器振膜状态估计方法的数据流图。如图1和图2所示，本发明实施例的扬声器振膜状态估计方法包括：

步骤S100、通过自适应滤波方法调整振膜位移模型的权重值，直至使得驱动电压估计值与驱动电压测量值的误差小于预定阈值。

其中，所述振膜位移模型根据当前时刻输入电流、当前时刻振膜相对速度估计值和当前时刻振膜位移估计值组成的向量与权重值向量的乘积计算下一时刻的振膜相对速度，并根据当前时刻振膜相对速度估计值、当前时刻输入电流和扬声器直流阻抗计算所述扬声器驱动电压估计值。也即，在本发明实施例的振膜位移模型中，权重值的数量较少。

具体地，图3为扬声器的电磁和机械振动模型的示意图。扬声器的振膜受电磁线圈产生的磁场的驱动而振动发声。在图3中，回路1为驱动线圈的等效电路。u_in为驱动电压，也即输入到驱动线圈(或称音圈)的输入电压；R为驱动线圈的电阻(也即，扬声器的直流阻抗)；L为驱动线圈的电感，l为驱动线圈的总长度，B为驱动线圈的磁体与振膜磁体隙缝的磁感应强度，也即，在驱动线圈不通电时，设置于驱动线圈的永磁体和振膜的永磁体的磁极间隙中的磁感应强度，其为一基本不变的值。i为回路1中电流也即驱动线圈中的电流，被驱动侧的耦合电压。

在图3中，回路2为与驱动线圈耦合的机械振动系统等效模型，其中，将机械力学系统中的不同参量等效为电路部件，以方便后续对于模型的进一步简化。电磁感应力由感应电压u_in产生，可等效为回路2中电流。其中，机械振动系统的质量以及振膜的力顺和机械振动系统的阻尼均对于施加的力具有不同的属性，将其分别等效为并列的电容、电感和电阻。

由此，可以得到输入电流i、驱动电压u_in、振膜速度v和振膜位移s之间的关系满足：

其中，m为扬声器的振膜质量，R_m为扬声器的机械阻尼，k为振膜的弹力系数。

如果直接使用公式(1)的模型来进行振膜位移估计，需要获取的参数太多，计算复杂。同时，Bl为非线性参数，其稳定性较差，同时，在计算时需要对扬声器的电-机系统和机械-声音系统进行建模，模型的权重值参数多，计算复杂。

由于电感主要对高频交流电有响应，其对于驱动电压u_in的影响可以忽略，因此，可以在模型中省略电感相关成分。同时，非线性参数Bl标幺化为1，忽略其非线性特性。对应地，在忽略模型中的非线性部分后，对应的位移被转换为相对位移参量。由此，可以得到作为本发明实施例基础的振膜位移模型：

其中，a、b、c为模型的权重值，s(k)表示时刻k振膜的相对位移。将振膜相对速度v(k)的系数取为1-b有利于使得模型更加稳定。

在公式(2)中，扬声器的直流阻抗R可以为预定值，也可以通过现有的方法计算或估计获得。优选地，扬声器的直流阻抗R可以根据中国专利申请CN104640053A中披露的方法估计获取。因此，在模型中R是已知的，不需要通过模型的迭代获取。

在此基础上，只需要更新公式(2)中的三个权重值a、b、c就可以对振膜相对位移s进行估计。

在本发明实施例中，将输入电流、估计得到的扬声器振膜相对速度和相对位移作为输入，将扬声器的驱动电压作为输出，通过自适应滤波方法来调整位移模型的三个权重值，直到驱动电压估计值u_e与驱动电压测量值u_d的误差e收敛(也即，小于预定的阈值)。此时，可以认为当前权重值对应的振膜位移模型能够较为准确地模拟扬声器的状态。该模型可以适用于进行后续的振膜位移估计。由此，可以实现在线进行扬声器状态的估计。

图4是本发明实施例中进行权重值调整的流程图。如图4所示，步骤S100可以具体包括如下步骤：

步骤S110、根据当前权重值a(k)、b(k)、c(k)对应的振膜位移模型计算下一时刻的振膜相对速度v(k+1)和振膜相对位移s(k+1)，并计算当前时刻的驱动电压估计值u(k)。

优选地，根据公式(2)，可以根据如下公式来执行步骤S110：

v(k+1)＝a(k)*i(k)+(1-b(k))*v(k)+c(k)*s(k)

s(k+1)＝ts*v(k)+s(k)

u(k)＝v(k)+R*i(k)

其中，ts为两个相邻时刻之间的时间长度，u(k)为驱动电压估计值。

步骤S120、根据当前时刻的扬声器驱动电压估计值和电压将测量值计算误差。

通常，通过计算差值既可以获得误差，也即：

e(k)＝umeas(k)-u(k)

e(k)为当前的误差，umeas(k)为驱动电压测量值。

步骤S130、在所述误差大于预定阈值时，基于自适应滤波方法根据扬声器参数的历史数据更新所述权重值。

具体地，可以采用各种适用于进行系统辨识的自适应滤波算法来进行权重值的更新。

优选地，可以采用最小均方算法(Least Mean Square，LMS)来进行权重值的更新。LMS算法可以使得滤波器的输出信号与期望响应之间的误差的均方值最小。在LMS算法中，定义权重向量W(k)＝[a(k),b(k),c(k)]，选取迭代因子mua,mub,muc，计算每次的权重向量值。具体地，按照下述公式来更新权重向量：

sa(k)＝ts*va(k-1)+sa(k-1)；

va(k)＝(1-b(k))*va(k-1)+c(k)*sa(k-1)+i(k)；

ua(k)＝va(k)；

a(k+1)＝a(k)+mua*e(k)*ua(k)；

sb(k)＝ts*vb(k-1)+sb(k-1)；

vb(k)＝(1-b(k))*vb(k-1)+c(k)*sb(k-1)-vest(k-1)；

ub(k)＝vb(k)；

b(k+1)＝b(k)+mub*e(k)*ub(k)；

sc(k)＝ts*vc(k-1)+sc(k-1)；

vc(k)＝(1-b(k))*vc(k-1)+c(k)*sc(k-1)+sest(k-1)；

uc(k)＝vc(k)；

c(k+1)＝c(k)+muc*e(k)*uc(k)

上述公式中，sa，sb，sc分别为振膜位移对权重向量a，b，c的梯度向量。ua，ub，uc分别是电压对权重向量a，b，c的梯度向量。va，vb，vc分别是振相对膜速度对权重向量a，b，c的梯度向量。

在步骤S130执行完成后，返回步骤S110，如此迭代，直至驱动电压估计值与驱动电压测量值的误差满足预期。

当然，本领域技术人员容易理解，也可以其它各种现有的自适应滤波算法来迭代更新所述模型参数。

步骤S200、根据最终确定的权重值对应的振膜位移模型估计扬声器的振膜相对位移。

基于该确定振膜位移模型来计算位移则可以准确定估计振膜位移。同时，由于需要调整更新的参数少，对于振膜位移模型的构建流程可以快速收敛。

在获得相对位移后，可以直接根据相对位移来执行相应的控制。在某些情形下，还需要进一步根据相对位移估计振膜的绝对位移。因此，本发明还可选地包括步骤S300，根据振膜相对位移与振膜绝对位移的预定关系以及计算获得的振膜相对位移获得振膜绝对位移。

如上所述，由于在模型中将BL标幺化为1，减少系统辨识参数，使得模型中估计获得的s(k)仅仅为相对位移而非绝对位移。由于绝对位移与非线性参数Bl相关，因此，其呈现出较强的非线性特性。在本发明实施例中，可以同时比较试验测量获得振膜绝对位移以及模型估计的振膜相对位移，建立两者的对应关系。在步骤S300中，基于该预先获得对应关系，可以根据振膜相对位移获取对应的振膜绝对位移。该对应关系可以体现为对应关系表，或根据对应关系建立的两者的比例函数曲线。

由于收敛快且具有较好的准确度，本发明的方法适于应用于需要实时估计扬声器振膜的扬声器驱动电路，其适于被设计为数字集成电路进行处理或以程序形式由通用处理器来执行。

通过将输入电流、估计得到的扬声器振膜相对速度和相对位移作为输入，将扬声器的驱动电压作为输出，将非线性的电机耦合系数标幺化为1获得更为简化的扬声器振膜位移模型，基于自适应滤波方法调整振膜位移模型的权重值，直至使得驱动电压估计值与驱动电压测量值的误差小于预定阈值，并根据最终确定的额权重值来对振膜相对位移进行估计，从而可以快速、准确地估计扬声器振膜位移，实现对于扬声器的精确控制。

以上所述仅为本发明的优选实施例，并不用于限制本发明，对于本领域技术人员而言，本发明可以有各种改动和变化。凡在本发明的精神和原理之内所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。