基于无线通信基站的三维定位方法与流程

本发明涉及移动通信定位技术领域，具体地指一种基于无线通信基站的三维定位方法。

背景技术：

随着基于位置的应用层出不穷，位置服务己经成为移动增值业务的重要组成部分，在移动通信领域具有广泛的应用前景，因此利用基站提供位置服务己经成为研究和应用热点。近年随着移动通信网络的迅速发展，更多的移动终端接入到移动通信网络中，越来越多的基站被建立起来，几乎遍布世界的每一个角落，为终端用户提供通信服务，所以实现移动终端的精准定位变得愈来愈重要。

移动通信网络中最基本的定位技术是基于基站的定位技术。移动通信定位技术在当前常用的主要有三种，即Cell-ID定位法、TDOA或AOA定位法、A-GPS定位法。影响定位精度的主要因素有：(1)多径传播对定位精度的影响；(2)NLOS(非视距)传播对定位精度的影响，NLOS传播是影响各种蝉窝网络定位精度的主要原因；(3)多址干扰对定位测量的影响；(4)基站个数及位置分布对定位的影响；(5)同一位置冗余测量的数据等。

Cell-ID定位法是根据移动终端所连接的蝉窝的位置来对用户的位置进行表示，该定位方法的精度较低，且定位精度差异大；TDOA或AOA定位法的基本原理是通过测量电波从移动终端传播到多个基站的传播时间或传播时间差来确定目标终端的具体位置，定位精度高于前一种定位法，但是考虑视距和非视距的情况，测量、噪声等因素会造成误差；A-GPS定位法是在GPS定位技术的基础之上，通过无线通信网络对辅助数据进行传输，它是一种十分快速的定位方法，具有定位精度高、定位速度快等优点，其缺点在于技术难度大、不能有效解决室内的定位问题。

技术实现要素：

本发明的目的是针对现有技术的不足之处，提出一种收敛速度快、时间复杂度低、精确度高的基于无线通信基站的三维定位方法。包括如下步骤：。

1)获取基站BS坐标，计算出移动终端MT到基站的传播时间；

2)从所有基站BS中选取一个为目标基站定为BS₁，其他基站定为BS_i，i为大于1的自然数；

3)计算其他基站BS_i到目标基站BS₁的距离差Dbb_i1，并筛选其他基站BS_i，更新计算移动终端MT到筛选后的其他基站BS_i的传播时间；

4)运行α-TDOA算法，得到移动终端MT的坐标(x,y,z)；所述α-TDOA的运算公式为：

其中，

上式中，α为加权因子，α∈(0,1)，A_i为第一参数；B_i为第二参数，C_i为第三参数；S_i为第四参数，(X₁,Y₁,Z₁)为目标基站BS₁的坐标，(X_i,Y_i,Z_i)为第i个其他基站BS_i的坐标；τ_i为移动终端MT到其他基站BS_i与目标基站BS₁的传播时间差；v为信号传播速度，取3*10⁸m/s。

优选地，所述步骤3)中使用k-NN分类算法，以其他基站BS_i到目标基站BS₁的距离差Dbb_i1作为判断标准进行筛选，每类中仅保留一个基站。

优选地，所述步骤3)中其他基站BS_i到目标基站BS₁的距离差Dbb_i1的计算公式为：

优选地，所述步骤4)之后还包括：

5)运行α优化算法，迭代优化加权因子α的值，根据优化后的加权因子α，更新计算得到移动终端MT的坐标(x,y,z)。

优选地，所述优化加权因子α的迭代次数为大于5次，每次迭代优化后舍弃超过1或者小于0的值。

优选地，所述α优化算法的公式为：

L＝ντ_i

其中：L为中间参数，Dmbi₁为移动终端MT与到达目标基站BS₁、其他基站BS_i的距离差。

本发明提供了一种基于基站的精确定位移动终端的方法，重点提出了一种在复杂环境下的高精度高效率定位。该方法中，我们考虑视距与非视距情况同时存在的传播环境，通过引入加权因子表达测量值与实际值之间的关系，设计算法进行计算及优化。另外，考虑到基站的数目较多，为了提高计算速度和保证精确度，首先对基站进行分类操作，在计算过程中，同一类中的基站仅选取其中的一个的测量值参与计算。试验结果表明，本发明提出的综合算法计算复杂度较低、收敛速度快、效率较高，最终计算出的终端位置坐标精确度高。

本发明与现有技术相比具有如下突出特点：

1.采用矩阵运算的形式计算终端坐标与优化算法，相比于现有技术，速度更快，时间复杂度更低；

2.本发明为提高定位精确度而设计的优化算法思路新颖，收敛速度快，每次迭代对不满足其应属范围的加权因子值进行舍弃，有效避免了误差较大测量值对结果的影响，大大提升了优化效率；

3.使用k-NN分类算法，依据基站与目标基站之间的距离进行分类，去除冗余基站，速度更快；实验表明，分类之后的定位精确度更高。

附图说明

图1为本发明的流程图。

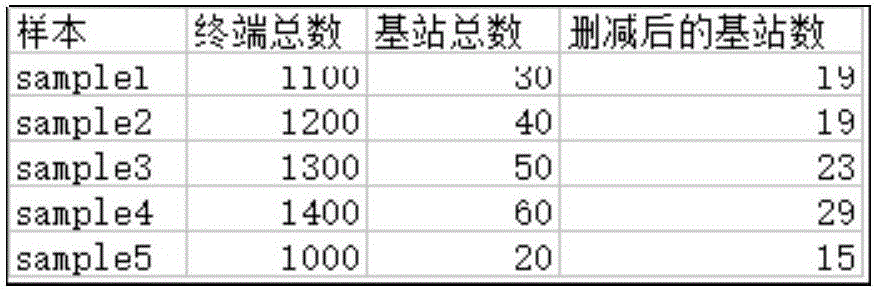
图2为样本数据表。

图3为仿真结果表1。

图4为仿真结果表2。

图5为误差5m内基站数目关于定位精度曲线图。

图6为误差5m内迭代次数关于定位精度曲线图。

具体实施方式

以下结合附图和具体实施例对本发明作进一步的详细描述。

本发明一种基于无线通信基站的三维定位方法引用了TDOA算法。

TDOA与时钟同步

信号到达时间差(Time Difference of Arrival,TDOA)是指同一移动终端(Mobile Terminal)MT发出的信号的到达不同基站(Base Station)BS的时间差。此种测量值的获取并不要求移动终端MT与基站BS的时钟同步，而仅要求所有基站BS时钟同步，因此在一定程度上降低了定位实施复杂度和计算复杂度。己有相关研究结果表明，基于TDOA的定位算法具有抗干扰能力强、计算精度高等优势，并在蝉窝通信网络、WLAN室内定位等诸多定位领域中得到普遍应用。假设在时间t内有两个相同的信号从移动终端MT分别发射向基站BS₁与BS₂，并且己知移动终端MT与基站BS₁的距离为D₁，与基站BS₂的距离为D₂，ε为发射端与接收端的时钟同步误差，那么基站BS ₁与基站BS₂接收到的信号时间差为：

根据上式可知，TDOA算法对收、发端的时钟同步没有要求，减少了时间误差变量，对构建算法模型具有一定的优化。

α-TDOA算法

综合考虑视距与非视距情况，测量、噪声等误差，发现误差对于数据的反映表现为测量值的偏大，基于其总是引起正的误差这一事实，同时参考定位效率与精确度，我们提出α-TDOA算法模型。首先随机初始化加权因子α(0<α<1)，使得：αvτ_i＝D_i-D₁。因此

通过移向可得

其中i＝2,3,...,N，用上式减去

可得到：

其中i＝3,4,...N,已知MT和BS_i的坐标分别是(x,y,z)和(X_i,Y_i,Z_i)，展开可以得到：

D_i²＝X_i²-2X_ix+x²+Y_i²-2Y_iy+y²+Z_i²-2Z_iz+z²

将上式结果代入(2)中：

其中i＝3,4,...N,我们把上面的式子重写为：

S_i+A_ix+B_iy+C_iz＝0

其中：

且

将上述N-2个等式写成矩阵的形式：

由此消除了D₁，那么MT的坐标(x,y,z)可以通过下面的方式获得：

本发明所需要的基站数目至少为5个。

如图1所示，本发明一种基于无线通信基站的三维定位方法的具体步骤为：

1)获取基站BS坐标，计算出移动终端MT到基站B的传播时间，作为TOA测量值。

2)从所有基站BS中选取一个为目标基站定为BS₁，其他基站定为BS_i，i为大于1的自然数。

3)计算其他基站BS_i到目标基站BS₁的距离差Dbb_i1，并筛选其他基站BS_i，更新TOA测量值并计算移动终端MT到筛选后的其他基站BS_i的传播时间。

使用k-NN分类算法，以其他基站BS_i到目标基站BS₁的距离差Dbb_i1作为判断标准进行筛选，每类中仅保留一个基站。Dbb_i1的计算公式为：

4)运行α-TDOA算法，得到移动终端MT的坐标(x,y,z)；所述α-TDOA的运算公式为：

其中，

上式中，α为加权因子，α∈(0,1)，A_i为第一参数；B_i为第二参数，C_i为第三参数；S_i为第四参数，(X₁,Y₁,Z₁)为目标基站BS₁的坐标，(X_i,Y_i,Z_i)为第i个其他基站BS_i的坐标；τ_i为移动终端MT到其他基站BS_i与目标基站BS₁的传播时间差；v为信号传播速度，取3*10⁸m/s。

5)运行α优化算法，迭代优化加权因子α的值，根据优化后的加权因子α，更新计算得到移动终端MT的坐标(x,y,z)。

优化加权因子α的迭代次数为大于5次，每次迭代优化后舍弃超过1或者小于0的值。

α优化算法的公式为：

L＝ντ_i

其中：L为中间参数，Dmbi₁为移动终端MT与到达目标基站BS₁、其他基站BS_i的距离差。

本发明中所需最少基站数目为五个。

仿真实验

以下仿真数据于个人PC环境中取得，其中操作系统：Win64位，处理器：Intel酷睿i5-6300HQ 2.3GHz，内存8GB，仿真软件为matlab R2015a 64位。我们从实际数据的测量结果文件中读取移动终端MT到基站BS的传播时间为TOA测量值，其中基站分布范围为1000×1000米(样本数据表如下所示)，仿真按照定位方法流程图依次执行，结果图2样本数据表所示：

图3为仿真结果表1，图3中误差范围表示计算出的移动终端MT位置坐标与实际终端位置坐标之间的欧氏距离。正确率定义为(计算出的移动终端MT的位置坐标与各自的实际位置坐标之间的欧氏距离在允许误差范围内的移动终端MT数目)/所有的移动终端MT数目。将给定的基站BS按其位置坐标进行分类，去掉多余的基站BS数据。根据本文算法模型，有5个基站BS的测量值P可以定位出终端坐标，更多的基站BS测量值用于提高定位的精确度。该表格表明：在同一允许误差范围内，随着参与计算的基站数目的增加，正确率也随之提高。表中部分样本在参与定位基站达到一定数目时无正确率数据，这是由在经过k-NN算法分类之后，筛选后的剩余基站数目小于表中所列出的数目而导致的。

图4为仿真结果表2，图中通过5次试验，结果表明：在同一允许误差范围内，随着加权因子α迭代次数的增加，计算出的终端位置坐标的正确率也越高；由表中数据还可以提取出如下重要信息：当迭代次数超过5次后，在允许误差为5米的条件下，普遍可以得到95％以上的正确率。

图5为误差5m内基站数目关于定位精度曲线图，图5中的结果显示，sample1-sample5中，终端误差范围在5m之内，正确率与定位基站数目的关系：sample1，定位基站数为5时，正确率最小，为33.09％；随着基站数的增加，正确率呈上升趋势，当定位基站数为13时，正确率趋于稳定，为98.73％；最高正确率超过99％；Sample2，定位基站数为5时，正确率最小，为29.75％；随着基站数的增加，正确率呈上升趋势，当定位基站数为19时，正确率最高，为97.42％；Sample3，定位基站数为5时，正确率最小，为12.23％；随着基站数的增加，正确率呈上升趋势，当定位基站数为23时，正确率最高，为87.77％；Sample4，定位基站数为5时，正确率最小，为16.93％；随着基站数的增加，正确率呈上升趋势，当定位基站数为29时，正确率最高，为93.93％；Sample5，定位基站数为5时，正确率最小，为51.7％；随着基站数的增加，正确率呈上升趋势，当定位基站数为15时，正确率最高，为99％。

图6为误差5m内迭代次数关于定位精度曲线图，图6中的结果显示，sample1-sample5中，终端误差范围在5m之内，正确率与迭代次数的关系，总体来说，收敛速度先快后慢，分别的：sample1，迭代1次，正确率为91.45％；5次迭代之后，正确率趋于稳定，接近99％；sample2，迭代1次，正确率为84.67％；随迭代次数增加，正确率呈上升趋势，最高为98％；sample3，迭代1次，正确率为90％；5次迭代之后，正确率趋于稳定，接近99％；sample4，迭代1次，正确率为83.21％；随迭代次数增加，正确率呈上升趋势，最高为98％；sample5，迭代1次，正确率为66.5％；5次迭代之后，正确率趋于稳定，接近99％。

本说明书中未作详细描述的内容属于本领域专业技术人员公知的现有技术。