一种上行链路大规模MIMO系统的信号检测方法与流程

本发明涉及无线通信技术领域，具体涉及一种大规模MIMO上行多用户信号检测的方法。

背景技术：

近两年来，通信界已经开始提出了5G技术的设想，新的研究工程已经在全球范围内开展起来，致力于5G的研究中心开始成立。2013年，在匈牙利首都布达佩斯召开的世界通信大会上，众多重要讲座和研讨会都围绕着5G技术来展开，并且成功解决了很多关键的技术理念，明确了关于5G标准化进程的时间节点，例如2016年到2018年将进行标准化，2020年开始商用。尽管5G还没有形成正式的标准，但是全世界范围内，包括政府的基金项目和企业的研发项目都在开展对5G关键技术的研究，争取主导权。

学术界已经提出，为了突破5G通信技术的瓶颈，5G移动通信系统将采用大规模多输入多输出MIMO传输技术来支持超过10Gbps的峰值传输速率和上百bps/Hz的频谱效率。随着天线数目的巨大提高，大规模MMO技术的优势得以充分挖掘的同时，其增加的计算复杂度超过了集成电路技术的发展。特别是大规模MIMO信号检测算法复杂度高，硬件实现难度大，成为下一代无线通信系统实用化亟待解决的问题。

传统的MIMO检测算法包括最优算法和次优算法。其中，最优的MIMO检测，包括最大似然和最大后验概率检测算法，它们是一个NP-hard问题,这两种算法能够达到最优的检测性能，但是因为其复杂度会随着天线数量指数增长，这给无线通信集成电路的设计带来严峻的挑战，而通常仅仅被用来当作性能对比的参考标准。次优算法又包括线性和非线性的算法。线性的检测算法包括MF、ZF和MMSE等，这些线性检测算法的算法可以通过格基规约的方法来提升性能。非线性的包括多级的干扰消除算法、树搜索、球形译码等。此外，还有一系列来自于机器学习和人工智能领域的非线性算法，比如基于邻近搜索的算法，它们来自于组合最优化理论，包括似然提升搜索，禁忌搜索。又比如PDA，置信传播，基于图的消息传递算法，以及MCMC算法等，这些算法也很有潜力能达到接近最优的性能。然而，在大规模MIMO系统中，很多传统MIMO检测算法变得不适应，同时有些低复杂度的算法的性能表现接近最优检测算法。

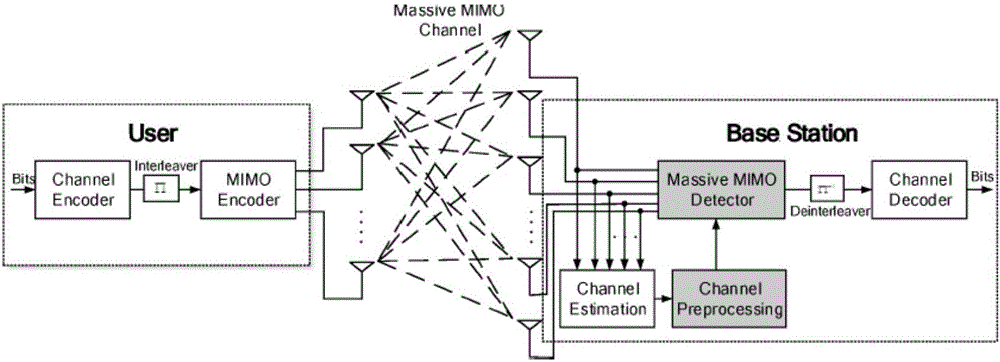
如图1所示，考虑一个多用户的大规模MIMO系统上行链路，该系统可以表示为大规模的基站天线(用N表示天线数目)同时服务于多个用户(用M表示用户数目)。多用户大规模MIMO上行链路的系统模型可以表示成y＝Hx+n，其中x＝[x₁,x₂,...,x_M]表示M×1的发送信号向量，其每个元素表示来自M-QAM的星座点符号每个元素的平均功率为E_s。n表示N×1独立同分布的复高斯噪声向量，每个元素的均值为0，方差为σ²。理想信道估计矩阵表示成H，维度为N×M，信道矩阵中的任意一项h_i,j表示从第j个发送天线到第i个接收天线的信道增益。y＝[y₁,y₂,…,y_N]^T表示N×1的接收向量。接收信噪比定义成N/M×1/σ²。

现有技术中，大规模MIMO上行链路多用户信号检测采用MMSE(Minimum Mean Square Error,最小均方误差)检测算法，MMSE检测算法为x＝(H^HH+σ²I)^-1H^Hy，由于其矩阵求逆和Gram矩阵H^HH的存在，算法复杂度分别为O(NM²)和O(M³)。当大规模MIMO系统中通信用户数较多时，MMSE检测算法的复杂度非常高，很难硬件实现。

技术实现要素：

本发明的目的是克服上述现有技术的不足，提供一种上行链路大规模MIMO系统的信号检测方法，将低复杂度的性能接近最优的，并且易于硬件实现的大规模MIMO上行链路多用户信号检测方法。

为实现上述方案，本发明技术方案如下：

一种上行链路大规模MIMO系统的信号检测方法，其特点在于，包括如下步骤：

步骤一：按照用户指定的天线数和调制方式配置检测层数；利用信道估计获取信道传递矩阵H以及利用干扰消除技术获取接收向量y，并做联合优化使接收信号的信噪比最大化。

步骤二：将MMSE检测算法转换成等效的增广矩阵，具体如下：

MMSE检测x＝(H^HH+σ²I)^-1H^Hy等效转换成增广矩阵的形式其中z＝σ^-1(y-Hx)，x为发送向量，H为信道矩阵，y为接收判决变量向量，σ²为噪声向量的方差，I代表单位向量。

步骤二：利用滤波矩阵的主对角线近似矩阵，计算迭代的初始解的估计x₀，公式如下：

x₀＝D^-1H^Hy，

其中，D表示滤波矩阵H^HH+σ²I的主对角线元素；

步骤三：按列计算迭代的矩阵求逆，公式如下：

其中，λ表示松弛因子，x_k,i表示k次迭代之后的预测发送向量，h_i表示矩阵的第i列，i＝1,2,…,M，k＝1,2,…；

步骤四：在迭代过程中计算软判决信息，并将计算结果输出，公式如下：

其中e_i代表单位向量，表示k次迭代之后用于计算软判决信息的信号。

所述MMSE检测的等效转换中，Gram矩阵的计算被分解，降低了之后迭代计算的复杂度。

所述初始解估计方法中，利用滤波矩阵的主对角线元素来近似求解初始解，降低迭代次数，提高算法收敛速度。

所述迭代Kaczmarz算法中，将算法修改为按列进行迭代，更加适应大规模MIMO信道矩阵的信道增强效应，提高迭代速度。

所述软判决信息的计算中，软信息的计算利用了迭代过程中的中间值，而不是等到迭代结束后计算，降低了计算复杂度。

一种上行链路大规模MIMO系统多用户信号检测的FPGA实现，利用了高层次工具进行信号检测方法的设计与实现。

与现有技术相比，本发明的有益之处在于：

做了FPGA的实现以及性能评估，与已有的基于Neumann级数、共轭梯度算法的检测方案相比，显著的改善了检测的性能，进一步逼近了最优的检测性能，同时维持了较低的计算复杂度。

附图说明

图1为大规模MIMO检测的原理图

图2为上行链路多用户大规模MIMO系统示意图

图3为本发明实施例中大规模MIMO上行链路多用户检测方法的流程示意图

图4为天线配置为128×16下本发明检测方法与Neumann级数方法和共轭梯度方法的性能仿真曲线

图5为天线配置为128×32下本发明检测方法与Neumann级数方法和共轭梯度方法的性能仿真曲线

具体实施方式

下面结合附图和实施例，对本发明的具体实施方式做进一步描述

参照图2所示，本发明首先介绍上行链路大规模MIMO系统模型，多输入多输出无线通信系统的框图如图2所示，大规模MIMO上行链路的系统模型可以表示成y＝Hx+n。

本实施例中提供了一种大规模MIMO上行链路多用户信号检测的方法，如图3中所示，以128×16天线的系统为例，即M为16，N为128，该检测方法主要包括：

信道获取和接收向量获取：

首先，由用户根据指定的天线数目和调制方式配置底层的检测层数，本实施例中为128和16；利用信道估计获取信道传递矩阵H以及利用干扰消除技术获取接收向量y，并做联合优化使接收信号的信噪比最大化。

等效转换：信道矩阵的规模为128×16，转换成实数形式后为256×32，由传统的MMSE检测算法可以得到x＝(H^HH+σ²I)^-1H^Hy为32×1的预测发送向量，对公式进行等效的变换，可以将公式代表的MMSE检测转换成等效的增广矩阵形式，如公式

其中z＝σ^-1(y-Hx)，可以发现，上式矩阵相乘展开之后与MMSE检测具有相同的形式。可以令s＝(z^T,x^T)^T，上面的公式可以写成其中和分别代表等效增广的信道传输矩阵和接收信号向量，转换后的增广矩阵规模为144×144。

公式(3)可以重写为以下两个公式：

(σI_2N H)s＝y (4)

(H^H -σI_2M)s＝0 (5)

初始化：由于矩阵H^HH+σ²I具有对角占优的特性，可以用该矩阵的对角近似作为算法的初始解。这样做可以很大程度上提高算法的性能，提高算法的迭代的速度，而只增加少量的复杂度。初始解可以表示为

x₀＝D^-1H^Hy＝D_invH^Hy (6)

其中D表示滤波矩阵H^HH+σ²I的主对角成分，D_inv表示D的逆矩阵。

本实施例中，初始化之后的迭代过程主要包括：通过将Kaczmarz算法运用到增广矩阵代表的线性系统中，从而可以避免Gram的矩阵的计算，同时也避免了等效滤波的计算。传统的Kaczmarz算法是按照矩阵行的形式进行迭代，本发明改进Kaczmarz算法的迭代形式，修改为按照按列的形式进行迭代，这一做法是利用了大规模MIMO系统的信道增强效应，能够提高算法迭代的速度。

让H＝(h₁,h₂,…,h_M)，I＝(e₁,e₂,…,e_M)，带入Kaczmarz算法到公式(5)可以得到

其中i＝1,2,…,M，k＝1,2,…，h_i表示H的第i列，e_i代表单位向量。

由s＝(z^T,x^T)^T，z＝σ^-1r，上式可以转换成以下两个公式

令r＝y-Hx，并且由z＝σ^-1r，公式(8)可以解得

其中i＝1,2,…,M，k＝1,2,…，并且有

最终经过k次外层迭代之后得到的向量即为所求的估计向量。

在本实施例中，可以调整松弛因子λ的大小，来改变算法迭代的收敛速度，通常，合适的松弛因子大小在0.7<λ<1.2之间。

软判决信息计算：本判决例可以通过以下的迭代公式计算软判决的信号，然后利用该信号计算软信息，

其中i＝1,2,…,M，k＝1,2,…。经过M次内层迭代之后，最终W^-1的估计值为利用该估计值可以计算出最终的软信息并输出结果，如公式(12)到(14)所示

其中和分别表示第b个比特位表示的0和1的符号子集，μ_i和v_i表示等效的信道增益和NPI方差，

本实施例还仿真平台进行验证，并且与传统的基于Neumann级数和共轭梯度的方法进行了性能比较。如图4和图5所示，在128×16和128×32天线配置下，本发明的检测算法在性能方面有显著的提升，更加逼近最佳的检测性能，而且复杂度方面也会更低。

以上显示和描述了本发明的基本原理、主要特征和优点。本行业的技术人员应该了解，上述实施例不以任何形式限制本发明，凡采用等同替换或等效变换的方式所获得的技术方案，均落在本发明的保护范围内。