一种基于线性加权最小二乘法的时间同步方法与流程

本发明涉及时间同步技术领域，具体涉及一种基于线性加权最小二乘法的时间同步方法。

背景技术：

时间同步技术是使整个无线传感器网络保持同一个时间标准的技术，它是一个分布式系统中的各个节点协同工作的最基本的支撑技术。不同的应用对时间同步的精度、范围、寿命、能量等有着不同的要求。当无线传感器网络用于变电站的带电检测和故障定位时，时间同步的精度直接影响到定位的准确性，虽然已经存在很多用在网络通信中的高精度的时间同步算法，然而，跟传统的通信网络不同的是，无线传感器网络中，传感器节点的计算能力和能量是有限的，传统用于计算机网路的NTP同步机制以及高成本的GPS同步机制并不适用。

现有的用于无线传感器网络的时间同步算法有参照广播同步协议(RBS)，双向成对同步协议(TPSN)，延迟测量同步协议(DMTS)和泛洪式时间同步协议(FTSP)等，还有基于这些算法的一些改进算法。RBS通过引入一个参考节点，周期性地广播同步数据包，接收节点记录并彼此交换收到数据包的时间来完成同步。TPSN则是典型的基于发送者-接收者的双向时间同步方法，子节点通过一种握手机制获取父节点的时标，用计算出的时钟偏差值调整本地时钟。延迟测量时间同步机制(DMTS)是一种简单直观的基于发送者-接收者的单向时间同步方法，DMTS通过测量估计数据包从发送到被接收过程中的各种延迟来完成同步。FTSP是一种基于发送者和接收者间的单向时间同步协议，节点通过广播来将节点的本地时间传给接收节点。相对于其他算法，FTSP算法由于采用线性拟合的方法估计时钟漂移和时钟偏移，精度较高。在统计学和参数估计理论中，最大似然法、最小方差无偏估计,卡尔曼滤波，最小二乘估计均可以用于参数的估计。最大似然法和最小方差无偏估计对消息的传输延迟的分布很敏感，若实际的传输延迟和假定的传输延迟模型不吻合，那么求出的估计量会有较大误差；而卡尔曼滤波方法对时钟的模型较为敏感，由于传感器节点配备的晶振价格较为低廉，晶振的稳定性易受环境影响，当同步周期较长时，若把节点时钟建立成一阶模型会有较大偏差。而最小二乘法对观测数据没有任何概率假设，所以无需任何先验知识，只需被估计量的观测信号模型即可估计信号参量。所以传统的FTSP算法一般采用线性最小二乘法来对数据进行线性拟合。但是线性最小二乘法是假设每次的观测噪声是一样的，而在无线传感器网络的每次同步过程中，越旧的时标对当前的观测带来的噪声越大，所以同等地对待各次观测量是不合理的。本发明介绍一种线性加权最小二乘法可以给予观测噪声小的观测量以较大的权值，降低观测噪声对同步精度的影响，从而进一步提高同步的精度。

技术实现要素：

本发明的目的在于提供一种基于线性加权最小二乘法的泛洪式时间同步方法，对泛洪式时间同步算法中的线性回归方法进行改进，消除观测噪声对同步精度的影响。针对节点搜集的时间对中的观测噪声，采用线性加权最小二乘法对时间进行线性拟合，在求得时钟漂移和时钟偏移的同时，降低观测噪声对同步精度的影响，从而实现高精度的同步。

一种基于线性加权最小二乘法的时间同步方法，其特征是，包含以下步骤：

S1、初始化时任意选定一节点作为根节点；此根节点周期性地广播同步数据包，同步数据包中包含MAC层的时标TimeStamp、根节点识别标志RootID、同步数据包的序列号SeqNum；其余节点为非根节点，非根节点在根节点记录myRootID中记录自己所属的根节点号，其时标TimeStamp与所属根节点的时标TimeStamp同步；

S2、非根节点在网络工作时启动一个超时定时器，若在约定时间内没有收到任何同步数据包，那么超时定时器加1，当超时定时器的值超过预设的值时，该节点定义自己为根节点，也周期性地广播同步数据包；

S3、非根节点接收到同步数据包时，必须对来自不同根节点的同步数据包进行过滤，只接受满足特定条件的同步数据包，并更新本地的线性回归表，按线性加权最小二乘法构造拟合直线，得到时钟漂移a和时钟偏移b；

S4、非根节点根据S3得到的时钟漂移a和时钟偏移b调整本地时钟，与根节点同步后，非根节点同样地广播同步数据包，其中，时标TimeStamp为同步后本地的时钟值，根节点识别标志RootID保持不变。

上述的一种基于线性加权最小二乘法的时间同步方法，其中，所述步骤S3中，满足下列2个条件之一的同步数据包才被接收：

条件一：RootID<myRootID；

条件二：(SeqNum>highestSeqNum)&&(RootID＝＝myRootID)；

其中，highestSeqNum表示同步的轮数，myRootID表示该节点所属的根节点号。

上述的一种基于线性加权最小二乘法的时间同步方法，其中，所述步骤S3中，构造拟合直线的方法是线性最小二乘法，其包含以下步骤：

令x_i为观测向量，为观测矩阵，θ为M维的被估计量，n_i为观测噪声，构造线性观测方程：

记X＝[x₀ x₁ … x_L-1]^T为L次的观测向量，对应的观测矩阵记为观测噪声向量N＝[n₀ n₁ … n_L-1]^T，则L次的观测方程为：

X＝Hθ+N (2)

令W＝diag(w₀,w₁,…,w_L-1)为权重矩阵，按照线性最小二乘法计算，得误差函数J_w(θ)：

J_w(θ)＝(X-Hθ)^TW(X-Hθ) (3)

其中，基于线性加权最小二乘算法中每次只用线性回归表中最新的K对时标来进行拟合，构造权重矩阵为：

W＝diag(0,…,0,r^K-1,…,r,1) (4)

令x_i＝Ts_i,h_i＝[Tr_i 1]，θ＝[a b]^T，a为时钟漂移，b为时钟偏移，则误差函数转换成：

其中，Ts_i为发送节点第i次同步时发送的时标，Tr_i为接收节点第i次接收数据包时的本地时标；

当

时，误差函数J(θ)最小，记可以求得：

现有的线性最小二乘法是假设每次的观测噪声是一样的，本发明介绍了一种线性加权最小二乘法，可以给予观测噪声小的观测量以较大的权值，使求出的时钟漂移更贴近真实传感器节点的晶振频率变化。通过降低观测噪声对同步精度的影响，可以进一步提高同步的精度。

附图说明

图1是本发明线性加权最小二乘法的步骤图。

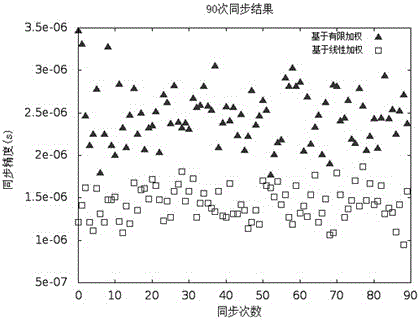
图2是本发明线性加权最小二乘法与传统的有限加权最小二乘法的精度仿真对比图。

图3是本发明中所述实施例的网络节点分布图。

具体实施方式

以下结合附图，通过详细说明一个较佳的具体实施例，对本发明做进一步阐述。

如图1所示，一种基于线性加权最小二乘法的时间同步方法，包含以下步骤：

S1、初始化时任意选定一节点作为根节点；此根节点周期性地广播同步数据包，同步数据包中包含MAC层的时标TimeStamp、根节点识别标志RootID、同步数据包的序列号SeqNum；其余节点为非根节点，非根节点在根节点记录myRootID中记录自己所属的根节点号，其时标TimeStamp与所属根节点的时标TimeStamp同步。

S2、非根节点在网络工作时启动一个超时定时器，若在约定时间内没有收到任何同步数据包，那么超时定时器加1，当超时定时器的值超过预设的值时，该节点定义自己为根节点，也周期性地广播同步数据包。所述预设的值由操作者根据本网络中节点数量、网络规模不同而选取不同的数值。

S3、非根节点接收到同步数据包时，必须对来自不同根节点的同步数据包进行过滤，只接受满足特定条件的同步数据包，并更新本地的线性回归表，按线性加权最小二乘法构造拟合直线，得到时钟漂移a和时钟偏移b。

S4、非根节点根据S3得到的时钟漂移a和时钟偏移b调整本地时钟，与根节点同步后，非根节点同样地广播同步数据包，其中，时标TimeStamp为同步后本地的时钟值，根节点识别标志RootID保持不变。

上述的一种基于线性加权最小二乘法的时间同步方法，其中，所述步骤S3中，满足下列2个条件之一的同步数据包才被接收：

条件一：RootID<myRootID；

条件二：(SeqNum>highestSeqNum)&&(RootID＝＝myRootID)；

其中，highestSeqNum表示同步的轮数，myRootID表示该节点所属的根节点号。

上述的一种基于线性加权最小二乘法的时间同步方法，其中，所述步骤S3中，构造拟合直线的方法是线性最小二乘法，其包含以下步骤：

令x_i为观测向量，为观测矩阵，θ为M维的被估计量，n_i为观测噪声，构造线性观测方程：

记X＝[x₀ x₁ … x_L-1]^T为L次的观测向量，对应的观测矩阵记为观测噪声向量N＝[n₀ n₁ … n_L-1]^T，则L次的观测方程为：

X＝Hθ+N (2)

令W＝diag(w₀,w₁,…,w_L-1)为权重矩阵，按照线性最小二乘法计算，得误差函数J_w(θ)：

J_w(θ)＝(X-Hθ)^TW(X-Hθ) (3)

其中，基于线性加权最小二乘算法中每次只用线性回归表中最新的K对时标来进行拟合，构造权重矩阵为：

W＝diag(0,…,0,r^K-1,…,r,1) (4)

令x_i＝Ts_i,h_i＝[Tr_i 1]，θ＝[a b]^T，a为时钟漂移，b为时钟偏移，则误差函数转换成：

其中，Ts_i为发送节点第i次同步时发送的时标，Tr_i为接收节第i次接收数据包时的本地时标；

当

时，误差函数J(θ)最小，记可以求得：

采用线性加权最小二乘法能有效提高同步精度。图2所示是在NS2网络仿真平台中搭建的仿真环境：节点数为30个，随机分布在100米*100米的范围内，节点时钟漂移为-10ppm～10ppm间的均匀分布，同步精度以节点两两之间的时间差的均值衡量，同步90次，同步间隔为20s。参与线性回归的时标对数K为8，基于有限加权最小二乘法的洪泛时钟同步协议FTSP同步误差为1.8μs～4.9μs，如▲所示；基于线性加权最小二乘法的FTSP算法的同步误差为0.8μs～1.9μs，如□所示。

图3为一个由7个节点组成的传感器网络，初始化时选择节点0为根节点，节点1、2在节点0的广播范围内，节点3、4、5在节点1的广播范围、节点5、6在节点2的广播范围内。

首先节点0每隔20s的间隔(interval)广播一个同步数据包，数据包中携带发送时的本地时标T_s。节点1和2收到数据包后记录下本地时标T_r，并用T_s和T_r作为一对时标更新线性回归表。对于大小为6(K＝6)的线性回归表，更新过程如下：当本地已收到的有效同步数据包数量小于6时，新获得的时标对直接加入线性回归表，大于6时，每次要丢弃回归表中最旧的那对时标，然后把新的时标放进去，即线性回归表中总存放的是最新的6对时标(Tr_L-6，Ts_L-6)、(Tr_L-5，Ts_L-5)、(Tr_L-4，Ts_L-4)、(Tr_L-3，Ts_L-3)、(Tr_L-2，Ts_L-2)、(Tr_L-1，Ts_L-1)。之后利用线性加权最小二乘法构造拟合直线，求出时钟漂移a和时钟偏移b。

权重r取0.9，待估计量θ＝[a b]^T，a为时钟漂移，b为时钟偏移。线性观测矩阵的误差函数可以转换成：

要令误差函数最小，则令：

记可以求得，当权重r取0.9时：

之后节点1和2的本地时钟调整为T_sync＝a×T_local+b，然后节点1和2开始像根节点一样广播同步数据包。节点3、4、5、6分别与节点1和2同步。由于节点5同时处于节点1和2的广播范围内，所以当节点5收到来自节点1或2的同步数据包时，节点5留下先收到的数据包，抛弃另一个数据包。对于最大跳数为2的网络，第一次全网同步需要2×K×interval的时间，之后每个同步周期便可进行一次全网同步。

尽管本发明的内容已经通过上述优选实施例作了详细介绍，但应当认识到上述的描述不应被认为是对本发明的限制。在本领域技术人员阅读了上述内容后，对于本发明的多种修改和替代都将是显而易见的。因此，本发明的保护范围应由所附的权利要求来限定。