一种非正交多址接入系统的功率分配方法与流程

本发明涉及无线通信技术领域，更具体地，涉及一种非正交多址接入系统的功率分配方法。

背景技术：

随着移动通信的快速发展，频谱资源变得越来越紧缺，面对飞速增长的移动业务需求，如何有效提高有限频谱资源的利用率成为第5代(5g)移动通信系统亟待解决的关键问题之一。由于具备有效提高系统容量的特点，非正交多址(non-orthogonalmultipleaccess，noma)技术被广泛认为是很有前途的多址技术。noma的基本思想是在发送端采用功率复用技术以非正交方式发送，主动引入干扰信息，在接收端通过串行干扰消除(successiveinterferencecancellation，sic)，接收机实现正确解调，虽然接收机的复杂度有一定程度的提高但却可以很好的提高频谱利用率。

在非正交多址接入系统中，功率资源在多用户间的分配策略也是研究的热点之一。根据非正交多址技术中接收端串行干扰消除的解码策略，为了达到系统最大吞吐量，发送端会把功率资源尽可能的向强用户(即距离发送端较近的用户)倾斜。这种情况会极大地损害弱用户(即距离发送端较远的用户)的通信性能，从实际应用的角度来看这种单一策略没有考虑到通信系统各用户资源分配的公平性。因此，必须采取相应措施来避免资源的利用不充分同时尽可能的提高系统性能。

技术实现要素：

本发明要解决的问题是：提出一种通过优化资源在多用户间的合理分配使系统总效用最大化的非正交多址接入系统的功率分配方法。

本发明为实现上述目的所提出的技术方案如下：

一种非正交多址接入系统的功率分配方法，包括以下步骤：

s1.初始化迭代系数和一组满足约束条件的功率分配方案；

s2.基于功率分配方案计算每个用户的信道均衡因子和松弛变量；

s3.基于计算的信道均衡因子和松弛变量的值对每个用户的功率分配进行优化；

s4.对每个用户优化后的功率分配进行整合，得到经过优化的功率分配方案，然后计算系统在优化的功率方案下的总效用；

s5.使用经过优化的功率分配方案重复执行步骤s2～s4直至系统总效用收敛，收敛时将对应的经过优化的功率分配方案作为最优的分配方案进行输出。

优选地，计算信道均衡因子的具体过程如下：

其中

其中k表示迭代次数，hn表示基站到第n个用户的信道响应；pn表示分配给用户n的发射功率；cn表示信道均衡因子，en定义为估计信号sn的均方误差。

优选地，所述计算松弛变量的具体过程如下：

优选地，所述对每个用户的功率分配进行优化的具体过程如下：

与现有技术相比，本发明的有益效果是：

本发明提出了一种非正交多址接入系统的功率分配方法，采用提出的功率分配方法，系统可在兼具公平性和尽可能提高和速率的情况下达到效用最大化。

附图说明

图1为本发明提供的方法的收敛过程示意图。

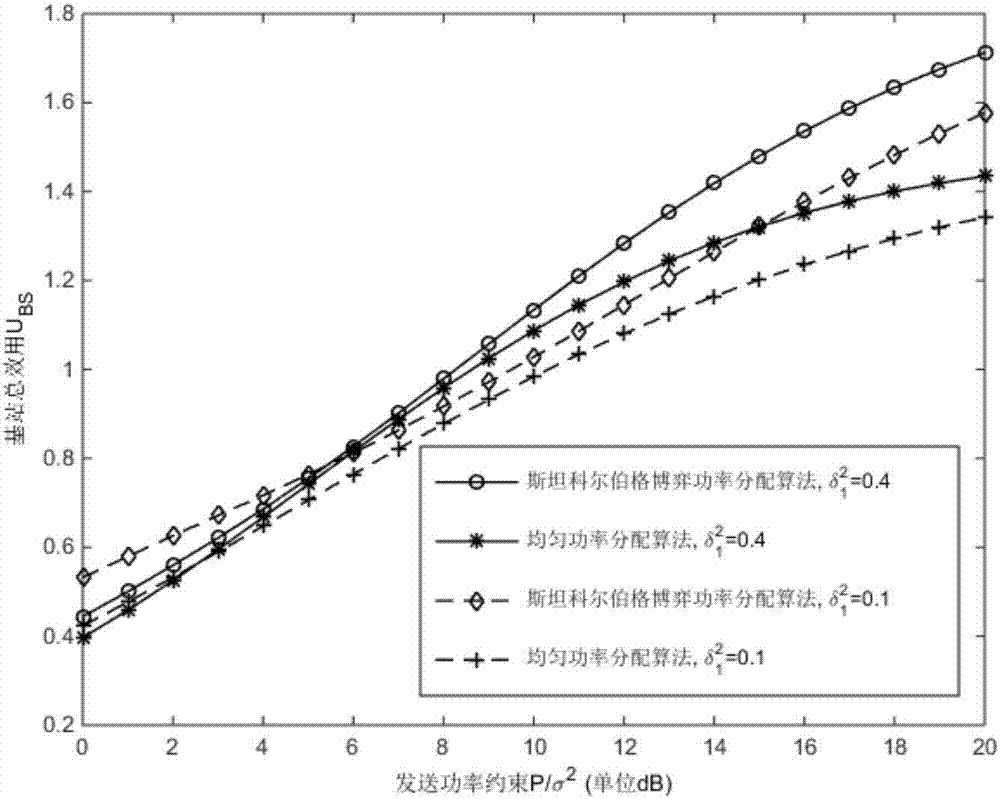
图2为对于不同信道响应的方差，在不同总发送功率约束下，基于本发明的功率分配方案和传统均匀功率分配方案在系统总效用上的对比图。

图3为在不同总发送功率约束下，基于本发明的功率分配方案和传统均匀功率分配方案在系统和速率上的对比图。

图4为本发明提供的方法流程图。

具体实施方式

附图仅用于示例性说明，不能理解为对本专利的限制；

为了更好说明本实施例，附图某些部件会有省略、放大或缩小，并不代表实际产品的尺寸；

对于本领域技术人员来说，附图中某些公知结构及其说明可能省略是可以理解的。

下面结合附图和实施例对本发明的技术方案做进一步的说明。

实施例1

本发明适用的通信系统模型由一个单天线基站和n个单天线接收用户组成；基站到第n个用户的信道响应表示为hn，其中假设基站端能够完全知道整个网络系统的信道状态信息(channelstateinformation，csi)；因此，基站能够适当地分配其发射功率以提高通信系统的通信性能；不失一般性，假设基站到各用户的信道响应满足不等式|h1|≤|h2|≤…≤|hn|。

根据非正交多址接入(noma)技术协议，发送端采用叠加编码技术，因此第n个用户的接收信号可表示为：

其中pn表示基站分配给第n个用户的发送功率，表示第n个用户端的加性高斯噪声。

各用户端执行串行干扰消除后，可将弱用户的信息完全解码并从干扰信号中去除，故第n个用户端的可达速率表达式为：

在此非正交多址无线通信系统中，基站和多用户间采用斯坦科尔伯格博弈的策略，基站(领导者)为分配给各用户的功率定价来最大化收入，用户(跟随者)根据基站的定价决定发送功率来最大化效用。

最大化基站(领导者)收入的优化问题可表述为：

最大化用户(跟随者)效用的优化问题可表述为：

其中，un＝rn-λnpn(λn)，表示用户n的效用函数，该效用函数由收入和支出两部分组成，收入部分由可达速率提供，支出部分由功率消耗所产生的的代价得到。

问题(3)和(4)构成斯坦科尔伯格博弈(主从博弈，基站为主动者，用户端为从动者)。

为求解主从博弈问题，我们首先用引理1将其转化为常见优化问题，通过凸优化的方法求解该优化问题来寻找原问题的斯坦科尔伯格均衡点。

引理1：给定单价当

满足条件时，用户n的最优发送功率满足等式

证明：通过求解问题(4)的最优解可得：

说明：当时，由于价格过高，用户n将不参与博弈；此时n个用户的通信系统将变为(n-1)个用户的通信系统；因此，我们只考虑(5)式满足的情况。

由此，原问题可重建为：

其中问题(8)为目标函数非凸的优化问题，我们通过引入松弛变量来处理。

引理2：令(a是正实数)，则有：

且等式右边的最优解为：a＝2^1-b.；

证明：f(a)是凹函数，则最优解可由求解可得。

用户n执行串行干扰消除后的接收信号为：

定义估计信号sn的均方误差(mse)函数：

上式通过展开计算可得：

通过凸优化知识可得使得en取得最小值的最优解

带回(12)式则有：

由上式可得：

然后，利用引理2和(15)，问题(8)被等价地转化为均方误差最小化问题：

其中，an为引入的松弛变量。当an和cn均取最优解时，目标函数为

问题(16)的目标函数是非线性的，接下来通过将其解耦成三个优化子问题，并采用交替迭代方法来求解信道均衡因子、松弛变量和功率分配。

具体来说就是在第k步迭代中，首先给定第(k-1)步迭代求得的最优功率值此时通过解以下优化问题来求解第k次迭代最优信道均衡因子：

该问题为凸问题且有闭式解：

得到第k步迭代的最优解代入求解如下优化问题来得到松弛变量an在第k次迭代时的最优值：

由引理2可得该问题闭式解：

其中：

得到第k步迭代的最优解和后，代入求解优化问题：

该问题是关于变量pn的一个凸优化问题，可以使用cvx工具箱直接求解。

由上面的分析可知，问题(18)和(19)均存在闭式最优解且问题(22)为凸问题，故每次迭代得到的目标函数值是单调非减；由于基站的发射总功率约束，使得该值存在上界，所以最终该迭代的解会收敛到一个稳定解。

在以上基础上，本发明提供的方法包括以下流程：

步骤0：设置系统参数；

步骤1：初始化迭代系数k＝0，给定一组满足约束条件的功率分配

步骤2：计算信道均衡因子和松弛变量：

forn＝1：n

计算

计算

其中

endfor

步骤3：求解功率分配问题：

步骤4：计算系统总效用，检验是否收敛，若收敛，结束此过程，当前所得功率分配结果即为最优功率分配方案；否则设置k＝k+1并以本次迭代所得功率分配结果为下次迭代初始值，跳转到步骤2。

实施例2

本发明效果可以通过下面仿真实验结果进一步说明，仿真实验的基本流程参照图4。

对于图1，设置系统中用户个数n＝3。基站到各用户的信道响应是均值为0、方差分别为的独立同分布复高斯随机变量，且基站总发射功率为p/σ²＝20db。

对于图2和图3，设置系统中用户个数n＝2。强用户的信道方差弱用户信道方差分别设置为及

(六)仿真分析与结果

图1是给定发送功率的条件下，本发明中的迭代算法的收敛过程图。由仿真结果图可以直观的看出该算法可以很快收敛到稳定解。

图2是对于不同信道响应的方差，在不同总发送功率约束下，基于本发明的功率分配方案和传统均匀功率分配方案在系统总效用上的对比。从图2可以看出在任意功率约束下，基于本发明的功率分配方案总是优于传统均匀功率分配方案。

图3是在不同总发送功率约束下，基于本发明的功率分配方案和传统均匀功率分配方案在系统和速率上的对比。从图3可以看出基于本发明的功率分配方案在保证系统和速率性能的前提下充分考虑了强弱用户间的公平性。所以不难看出，基于本发明的功率分配方案的性能优于传统均匀功率分配方案方案。

显然，本发明的上述实施例仅仅是为清楚地说明本发明所作的举例，而并非是对本发明的实施方式的限定。对于所属领域的普通技术人员来说，在上述说明的基础上还可以做出其它不同形式的变化或变动。这里无需也无法对所有的实施方式予以穷举。凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明权利要求的保护范围之内。