一种私钥定长的密文策略属性基加密方法与流程

本发明涉及信息安全技术领域，具体是一种私钥定长的密文策略属性基加密方法。

背景技术：

作为一种较成熟的加密方式，公钥加密已经被广泛采用，但是传统的公钥加密在实现过程中需要借助一对密钥——公钥和私钥，其中公钥被加密方用来加密明文信息、私钥被解密方用来解密密文信息，而且此两密钥具有一一对应性。但在当前被广泛研究并付诸实践的共享存储、云计算、云制造等网络场景下，用户数量、被访问数据量均较为巨大，且数据拥有者需要与数据使用者维持一对多的关系，因此将传统公钥加密策略应用于此类场景时将会导致系统工作效率较低、系统维护开销较大，甚至出现系统无法正常工作的情况，给信息的安全传输及高效的访问控制带来了较大挑战，属性基加密能够较好地解决以上问题。

属性基加密可细分为密文策略属性基加密(CP-ABE)和密钥策略属性基加密(KP-ABE)。其中，CP-ABE的核心思想是，加密方将加密策略表示为访问结构(即公钥)并完成信息的加密，解密方只有在拥有满足该访问结构的属性集合(即私钥)时才能解密成功，此时的隐私策略由加密方制定，不但能够实现数据加密，还能通过对潜在数据解密方进行筛选完成对数据的访问控制。例如，借助于该类策略，数据提供者制定访问策略“(计算机学院AND教师)OR教务处职员”，并借助于这一策略完成对数据的加密操作，由此限定只有满足这一访问策略的用户才能完成对数据的解密及使用。显然，此类解决方案较好地处理了将传统公钥加密应用于新型网络场景中时所遇到的系统开销大、数据使用者信息无法预先获取、公私钥一一对应等问题，对云计算等新型网络场景具有更强的适用性。

作为属性基加密的核心基础部件，访问结构起着举足轻重的作用。门限结构、LSSS矩阵、与门及分布矩阵等多种结构已被采用来开发CP-ABE，但这些结构在表达能力及表达效率等方面并不理想。

简化有序二叉决策图(ROBDD)不但能够实现对任意布尔函数的极简表示，还能高效完成布尔变量及函数间的任意布尔操作，因此该结构是一种属性基加密策略中访问结构的理想选择。基于这一出发点，本发明对访问结构进行深入研究，充分开发ROBDD的高效性能，以求进一步提升CP-ABE在工作效率、扩展性等方面的性能表现。

与本发明相关的基础理论知识

(1)访问结构

本质上而言，访问策略是一条规则R，能够根据输入属性集合的状态无异议的得出1或0，只有当该规则对属性集S返回1时，称S满足R，记为与之相对的是S不满足R，记为

访问结构便是上述访问策略的直观表达，具体表现形式有阈值门、与或树等。

(2)双线性映射及双线性群

①双线性映射：存在素数阶为p的群G₀、G₁，且群G₀的生成元为g，若映射e:G₀×G₀→G₁具有以下性质，则称该映射为双线性映射：

a)双线性性：对于任意u,v∈G₀及a,b∈Z_p，满足e(u^a,v^b)＝e(u,v)^ab；

b)非退化性：e(g,g)≠1。

②双线性群：如果群G₀内的运算及双线性映射e:G₀×G₀→G₁均具备可计算性，则称G₀为双线性群。

(3)简化有序二叉决策图

①二叉决策图：对于从{0,1}ⁿ到{0,1}的布尔函数f(x₁,x₂,…,x_n)，二叉决策图是用于表示布尔函数族#f(x₁,x₂,…,x_n)的一个有向无环图，它满足：

a)二叉决策图中结点分为根结点root、终结点和内部结点三类。

b)终结点仅有2个，分别表示布尔常量0和1。

c)每个非终结点u具有四元组属性(f^u,var,low,high)，其中，f^u表示结点u所对应的布尔函数，f^u∈#_πf(x₁,x₂,…,x_n)(如果u是根结点，则f^u＝f(x₁,x₂,…,x_n))；var表示结点u的标记变量；low表示u.var＝0时，结点u的0分支子结点；high表示u.var＝1时，结点u的1分支子结点。

d)每个非终结点均具有两条输出分支弧，将它们和各自的两个分支子结点连接在一起。结点u和u.low的连接弧称为0-边，结点u和u.high的连接弧称为1-边。

e)二叉决策图的任一有向路径上，布尔函数f(x₁,x₂,…,x_n)中的每个变量至多出现一次。

在图形表示中，通常用方框表示终结点(即)，用圆圈表示其它结点，假设结点之间的连接弧的方向向下，0-边用虚线表示，1-边用实线表示。

②有序二叉决策图：对于从{0,1}ⁿ到{0,1}的布尔函数f(x₁,x₂,…,x_n)和给定变量序π，在表示布尔函数族#f(x₁,x₂,…,x_n)的二叉决策图中，如果任一有向路径上的变量x₁,x₂,…,x_n均以变量序π所规定的次序依次出现，则称该二叉决策图为布尔函数f(x₁,x₂,…,x_n)的有序二叉决策图。

③简化有序二叉决策图：对于某一有序二叉决策图，如果其内部节点满足：

a)对于节点u，u.low≠u.high。

b)对于两个节点u和v，满足(u.low≠v.low)∨(u.high≠v.high)∨((u.low≠v.low)∧(u.high≠v.high))。

则进一步称该有序二叉决策图为简化有序二叉决策图。

技术实现要素：

本发明的目的在于解决现有技术中存在的技术问题，提供一种私钥定长的密文策略属性基加密方法。该方法对新型ROBDD访问结构、与ROBDD访问结构相关的策略表示方法、用户可满足性判定、CP-ABE所包含的多个具体算法进行了形式化表述；该方法在算法时间复杂度、存储空间占用量、安全性等方面都具有较好表现，并且能够支持任意布尔表达式所表述的访问策略、生成占用空间极小且定长的私钥、实现快速解密，并最终使系统工作效率高，系统维护开销小。

实现本发明目的的技术方案是：

一种私钥定长的密文策略属性基加密方法，具体实现过程中，共包含4个实体：数据加密方(即数据拥有者)、数据解密方(即数据使用者)、授权中心、云端存储服务器，具体实现步骤如下：

1)系统建立：由授权中心执行Setup算法，选择双线性群G₀、G₁，定义双线性映射e:G₀×G₀→G₁，通过运算生成系统公钥PK和主密钥MK；

2)明文加密：由数据加密方执行Encrypt算法，根据预先定义的访问策略生成相应的ROBDD访问结构，并基于该ROBDD访问结构进一步完成对明文数据M的加密操作，最终生成密文数据CT；

3)私钥生成：由授权中心执行Keygen算法，根据用户提供的属性集合S，通过与步骤2)中的ROBDD访问结构间的路径匹配生成用户私钥SK；

4)密文解密：由数据解密方执行Decrypt算法，主要操作是借助于递归算法实现自身所拥有私钥SK与ROBDD访问结构间的匹配，最终结果有两种：如果私钥SK合法则解密成功并输出明文数据M，否则解密失败；

经过上述步骤，数据加密方借助于ROBDD实现了访问策略的高效表达及实现，并进一步完成了数据的高效加密工作；数据解密方能够获得授权中心为其生成的定长私钥，并在私钥合法的情况下完成对密文的快速解密。

所述步骤1)中，授权中心选择双线性群G₀、G₁，定义双线行映射e:G₀×G₀→G₁；随机选择素数p阶循环群Z_p中的元素y,t₀,t₁,…,t_n-1,t₀',t₁',…,t_n-1'；令最终生成系统公钥和主密钥

所述步骤2)中,数据加密方首先需要根据具体的访问策略生成相应的布尔函数，并进一步构造与该布尔函数相应的ROBDD结构；在该ROBDD结构的基础之上，按照由上而下、从左至右的顺序对所有节点进行重新编号，将最终得到的ROBDD访问结构表述为：

上述(1)式中ID、I分别为ROBDD结构中所含全部非终节点的编号、全部变量所组成的集合，本质上可使用四元组<id,i,high,low>表示，id为节点编号、i为节点上的属性编号、high为本节点1-分支节点编号、low为本节点0-分支节点编号，high域及low域的作用是维护节点间的连接关系；其中编号为0和1的节点具有固定的表示意义，即终节点

进一步的，在ROBDD结构中，根节点root与终节点间的任意路径均称为有效路径；若属性集S中的属性能与ROBDD结构中的任意一条有效路径相匹配，则称属性集S满足访问结构ROBDD，记为

进一步的，数据加密方，借助于访问结构完成对数据为M∈G₁的加密操作；其中ROBDD访问结构所含有效路径的总数为T，并将其表示为R＝{R₀,R₁,…,R_T-1}。加密操作具体执行如下：

随机选择s∈Z_p并计算定义C_Rt(R_t∈R)为与路径直接相关的密文组件，其数学表述为：

上述(2)式中，R_t为路径编号，I_t为路径R_t上所包含的全部属性之集合，最终生成的密文表示为

在该步骤中，主要的计算量为群G₀中的|T|+1次指数运算和∑|I_t-1|次乘法运算、群G₁中的1次指数运算和1次乘法运算；密文的主要存储量包括访问结构ROBDD、群G₀中的|T|+1个元素及群G₁中的1个元素。

所述步骤3)中,授权中心根据用户提供的属性集S生成用户私钥SK，对于默认私钥生成操作具体包含如下步骤：

①查询ROBDD结构中编号为2的节点(即root)，将其定义为当前节点，设置t_SK＝0；

②读取当前节点中保存的信息对于其中所含的属性i：如果i∈S∧i＝i，执行t_SK+＝t_i，转到③；如果执行t_SK+＝t_i'，转到④；

③根据当前节点的high域信息查找其1-边子节点，如果到达终节点(或)，转到⑤；否则将该子节点定义为当前节点并转到②；

④根据当前节点的low域信息查找其0-边子节点，如果到达终节点(或)，转到⑤；否则将该子节点定义为当前节点并转到②；

⑤随机选择r∈Z_p，计算

经过上述步骤，最终生成的用户私钥为

该步骤中主要的计算量为群G₀中的2次指数运算，用户私钥占用的存储空间为群G₀中的2个元素，即私钥定长。

所述步骤4)中,解密用户借助于自身拥有的私钥SK完成对密文CT的解密工作，假设待解密的密文为解密用户拥有的私钥为解密过程可通过以下递归算法实现：

A解密用户首先查询ROBDD结构中编号为2的节点(即root)，将其定义为当前节点；

B读取当前节点中保存的信息对于当前节点中所含的属性i，如果i∈S∧i＝i，转到C；如果转到D；

C根据当前节点的high域信息查找其1-边子节点：

a)若1-边子节点为终节点终止递归算法，返回解密失败；

b)若1-边子节点为终节点转到E；

c)若1-边子节点为非终节点，将其定义为当前节点并转入B继续执行；

D根据当前节点的low域信息查找其0-边子节点：

a)若0-边子节点为终节点终止递归算法，返回解密失败；

b)若0-边子节点为终节点转到E；

c)若0-边子节点为非终节点，将其定义为当前节点并转入B继续执行；

E若当前已成功匹配的有效路径为R_t，依次计算：

提示解密成功并返回密文M；

该步骤中，Decrypt算法的最大计算量为2次线性对计算、G₁中的2次乘法运算，此时解密算法的计算量与属性数量、密文长度等均无关，为常量，则用户能够成功高效的完成密文的解密工作并得到明文数据。

有益效果：由上述技术方案可以看出，本发明首先提出的一种私钥定长的密文策略属性基加密方法，是基于ROBDD的访问结构，随后基于ROBDD设计完成了一种CP-ABE方法。与现有技术相比，由于本发明采用ROBDD重新设计CP-ABE中的访问结构，使得新访问结构具备更强表达能力及扩展性，能够在不增加系统开销的情况下同时支持正值属性及负值属性，能够支持属性在访问策略中的多次出现，能够完成AND，OR及NOT等属性间的所有操作；进一步的，本专利基于ROBDD访问结构重新构造的CP-ABE在算法时间复杂度、存储空间占用量、实现快速解密等方面都具有较好表现。

附图说明

图1是本发明实施例中CP-ABE的整体框架示意图；

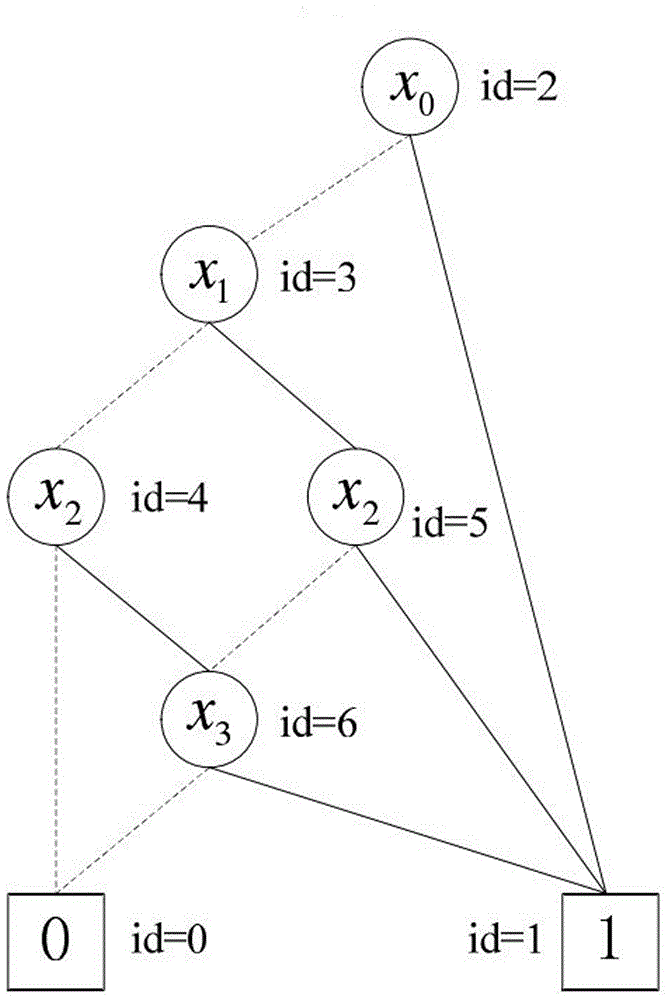
图2是本发明实施例中布尔函数f₁(x₀,x₁,x₂,x₃)的ROBDD表示图；

图3是本发明实施例中KeyGen算法的流程图；

图4是本发明实施例中Decrypt算法的流程图；

图5是本发明实施例中不同属性集、密钥元素及解密路径间的关系图。

具体实施方式

下面将结合附图和实施例对本发明做进一步阐述，但不是对本发明的限定。

实施例：

一种私钥定长的密文策略属性基加密方法，以ROBDD作为访问结构而设计CP-ABE方案的整体框架示意图如图1所示，共包含4个实体：数据加密方，即数据拥有者；数据解密方，即数据使用者；授权中心；云端存储服务器。该加密方法主要包含以下4个基本算法：

1)Setup算法，由授权中心执行，主要进行以下操作：选择阶为p的双线性群G₀，具有生成元g，双线行映射表示为e:G₀×G₀→G₁；随机选择Z_p中的元素y,t₀,t₁,…,t_n-1,t₀',t₁',…,t_n-1'。令进一步生成系统公钥及主密钥

2)Encrypt(PK,M,ROBDD)算法，由数据拥有者执行，主要完成数据的加密操作，加密用户拥有的数据为M∈G₁，所使用的访问结构为假设该结构中所含有效路径的总数为T，并将其表示为R＝{R₀,R₁,…,R_T-1}，加密操作执行如下：

随机选择s∈Z_p并计算定义C_Rt(R_t∈R)为与路径直接相关的密文组件，其数学表述为该式中，R_t为路径编号，I_t为路径R_t上所包含的全部属性之集合。最终生成的密文表示为

在上述加密算法中，主要的计算量为群G₀中的|T|+1次指数运算和∑|I_t-1|次乘法运算、群G₁中的1次指数运算和1次乘法运算；密文的主要存储量包括访问结构ROBDD、群G₀中的|T|+1个元素及群G₁中的1个元素。

3)Keygen(ROBDD,S,MK)算法，由授权中心执行，以根据用户提供的属性集S生成用户私钥SK。KeyGen算法的流程图如图3所示，

用户拥有的全部属性用集合S表示，对于默认KeyGen算法运行如下：

①查询ROBDD结构中编号为2的节点(即root)，将其定义为当前节点，设置t_SK＝0；

②读取当前节点中保存的信息对于其中所含的属性i：如果i∈S∧i＝i，执行t_SK+＝t_i，转到③；如果执行t_SK+＝t_i'，转到④；

③根据当前节点的high域信息查找其1-边子节点，如果到达终节点(或)，转到⑤；否则将该子节点定义为当前节点并转到②；

④根据当前节点的low域信息查找其0-边子节点，如果到达终节点(或)，转到⑤；否则将该子节点定义为当前节点并转到②；

⑤随机选择r∈Z_p，计算最终生成的用户私钥为

该算法主要的计算量为群G₀中的2次指数运算，用户私钥占用的存储空间为群G₀中的2个元素，即私钥定长。

4)Decrypt(CT,SK)算法，由解密用户执行，以使用自身拥有的私钥SK完成对密文CT的解密工作。Decrypt算法的流程图如图4所示，

假设待解密的密文为解密用户拥有的私钥为解密过程可通过简单的递归算法实现：

A解密用户首先查询ROBDD结构中编号为2的节点(即root)，将其定义为当前节点；

B读取当前节点中保存的信息对于当前节点中所含的属性i，如果i∈S∧i＝i，转到C；如果转到D；

C根据当前节点的high域信息查找其1-边子节点：

a)若1-边子节点为终节点终止递归算法，返回解密失败；

b)若1-边子节点为终节点转到E；

c)若1-边子节点为非终节点，将其定义为当前节点并转入B继续执行；

D根据当前节点的low域信息查找其0-边子节点：

a)若0-边子节点为终节点终止递归算法，返回解密失败；

b)若0-边子节点为终节点转到E；

c)若0-边子节点为非终节点，将其定义为当前节点并转入B继续执行；

E若当前已成功匹配的有效路径为R_t，依次计算：

提示解密成功并返回密文M。

由以上推导可知，该步骤中，Decrypt算法的最大计算量为2次线性对计算、G₁中的2次乘法运算，此时由此可知，解密算法的计算量与属性数量、密文长度等均无关，为常量，则用户能够成功高效的完成密文的解密工作并得到明文数据。

假设共有3位解密用户，拥有属性集分别为S₁＝{x₀,x₁}、S₂＝{x₁,x₂}、S₃＝{x₁,x₃}，在使用图1中ROBDD结构进行加密的情况下，此3位用户的解密路径、与之相应的密钥元素如下图5所示，表明他们能够解密成功并获得明文。

本发明实施例还提供相应的基于简化有序二叉决策图的访问结构的构造方法，以下将进行详细说明：

(1)基于ROBDD的访问结构

本发明提出了ROBDD访问结构，该访问结构是非单调的，能够支持正值属性及负值属性，并可实现属性间的与、或、非等任意布尔操作，能够实现对访问策略的灵活高效表达。在给定访问策略后，生成ROBDD访问结构的过程主要包含以下几步骤：

①访问策略的布尔函数表示

首先将访问策略中的各个属性使用变量x_i(1≤i≤n)表示，其中n为属性总量，继而将使用自然语言描述的访问策略转换为布尔函数表示f(x₁,x₂,…,x_n)。

其中需要指出的是门限运算的布尔函数表达转换方法：门限运算简记为T(t,n)，表示共有个属性总量为n，拥有其中任意t个元素的用户便能够完成门限运算T(t,n)，对于加密系统而言，完成门限运算T(t,n)便意味着解密成功。

关于构造门限运算T(t,n)的布尔函数表达，首先从n个属性中任意选取t个互不相同的属性构成组合，根据组合数公式可以得知此类组合共有C(n,t)个，记为Com₁,Com₂,…,Com_C(n,t)；

对上述C(n,t)个组合中分别包含的t个元素进行合取操作，并将结果记为Con₁,Con₂,…,Con_C(n,t)；

将上述C(n,t)个合取结果进行析取操作，得出门限运算T(t,n)的布尔函数表达，记为

②根据布尔函数获得相应的ROBDD表示

针对同一函数，不同的变量序会生成截然不同的ROBDD结构，其各自占用的表示空间(结构所含节点数量)也差别巨大。因此，在通过应用递归过程构造布尔函数的ROBDD表示之前应规定变量序π。根据布尔函数构造其ROBDD表示的算法如下：

算法：ROBDD的构造

输入：布尔函数f及变量最大编号n-1

输出：布尔函数f在变量序π:x₀<x₁<…<x_n-1下的ROBDD表达

按照由上而下、从左至右的顺序对所有节点进行重新编号，并将最终得到ROBDD访问结构表述为：

上述(1)中ID、I分别为ROBDD结构中所含全部非终节点的编号、全部变量所组成的集合。本质上可使用四元组<id,i,high,low>表示：id,为节点编号、i为节点上的属性编号、high为本节点1-分支节点编号、low为本节点0-分支节点编号，high域及low域的作用是维护节点间的连接关系。需要指出的是，编号为0和1的节点具有固定的表示意义，即终节点

有效路径：在ROBDD结构中，根节点root与终节点间的任意路径均称为有效路径。

对ROBDD结构的满足性：给定访问结构ROBDD及属性集S，如果S中的属性能够与ROBDD结构中的任意一条有效路径相匹配，则称属性集S满足访问结构ROBDD，记为

例如：根据访问策略得到布尔函数、并最终构造ROBDD结构。其中访问策略为：拥有属性x₀或者属性(x₁,x₂,x₃)中的任意两个属性的用户能够完成解密。

根据上述访问策略，得出对应的布尔函数为：f₁(x₀,x₁,x₂,x₃)＝x₀+x₁x₂+x₁x₃+x₂x₃。

对于上述布尔函数，在变量序π:x₀<x₁<x₂<x₃下的ROBDD构造过程如下：首先根据香农分解规则并借助上述递归算法实现布尔函数的ROBDD表示；随后对结构中所含的节点进行重新编号，并最终得到相应的ROBDD访问结构，如图2所示，其数学表达式为

(2)基于ROBDD的CP-ABE构造

本专利提出的CP-ABE方案支持正值属性i和负值属性因此为了叙述方便，使用统一标识i(取值为i或)表示属性。假设系统属性集为N，其中所含n个元素编号为{0,1,…,n-1}。