一种基于符号检测的MMSE干扰对齐方法与流程

本发明属于无线通信系统领域，具体的属于无线通信干扰信号处理方法。

背景技术：

近来，为了消除蜂窝移动通信系统小区间干扰，业界提出了干扰对齐(interferencealignment)，并且针对该技术开展了广泛的研究。为了实现干扰的对齐，发射机和接收机必须进行联合设计，这一点一般情况下比较难实现。为了解决这个问题，现有技术中提出了很多不同的迭代设计方法，包括最小干扰泄露(minimizingtheinterferenceleakage，mil)、最大化信干噪比(maximumsignal-to-interference-plus-noiseratio，max-sinr)、最小均方误差(minimum-mean-square-error，mmse)等。作为一种的干扰对齐设计方法，mmse在各种不同的通信场景下的设计得到了广泛的研究，体现了最佳的性能。

现有技术中在mmse的干扰对齐计算中，对于具有k个发射端和k个接收端的对称mimo干扰系统，为了简化计算，对于发射码流向量做了取统计平均处理，并将发射端预编码矩阵初始化为随机酉矩阵，使用该随机酉矩阵和信道矩阵进行迭代计算获得最优的预编码矩阵和合并矩阵。其具体方法流程如下：

步骤1：初始化随机酉矩阵vi

步骤2：

步骤3：

步骤4：

步骤5:返回步骤2，持续迭代α次数。

其中orth{a}表示对矩阵a进行正交化处理，变量α为迭代次数，变量为信噪比。

在上述的迭代计算中，为了在计算中消除未知的码流sj的影响，传统的方法在计算ui和vi的过程中采取了对sj取统计平均的处理。然而，在实际计算中，由于实际的码流与取统计平均处理的码流存在一定误差，并且一般情况下，干扰信道中用户数越少，统计意义下的误差越大。但若在干扰对齐迭代计算中直接使用实际发射码流向量进行计算，迭代计算中可能由于符号检测误差太大而引起干扰无法较好的对齐，尤其是在高信噪比环境。

技术实现要素：

本发明的目的在于克服上述不足，提出了一种基于符号检测的mmse干扰对齐方法(symbol-detection-aided-mmseia，sda-mmseia)，能够降低误码率，提升均方误差性能。

为了达到上述目的，本发明包括以下步骤：

s1：使用信道矩阵h和初始化的预编码矩阵进行迭代运算，获得第一合并矩阵u1和第一预编码矩阵v1；

s2：使用所述第一合并矩阵u1和接收信号y得到发射码流

s3：使用信道矩阵h、所述发射码流和所述第一预编码矩阵v1进行迭代运算，获得第二合并矩阵u2和第二预编码矩阵v2；

s4：使用第二合并矩阵u2和接收信号y得到最优的发射码流

其中，步骤s1具体包括：

s11：初始化发射端的预编码矩阵v以及迭代计数器m，将m初始化为0；

s12：根据信道矩阵h和所述预编码矩阵v获得第一中间合并矩阵u′，

s13：根据所述信道矩阵h和所述第一中间合并矩阵u′获得第一中间预编码矩阵v′；

s14：使用所述第一中间预编码矩阵v′替换所述预编码矩阵v，将m值加1，若m的值不等于α-β，则返回步骤s12进行迭代运算，若m的值等于α-β，将得到的u′作为第一合并矩阵u1，将得到的v′作为第一预编码矩阵v1。

其中，步骤s3具体包括：

s31：初始化迭代计数器n为0；

s32：根据所述信号矩阵h、所述发射码流和所述第一预编码矩阵v1获得第二中间合并矩阵u″；

s33：根据所述信号矩阵h、所述发射码流和所述第二中间合并矩阵u″获得第二中间预编码矩阵v″；

s34：使用所述第二中间预编码矩阵v″替换所述第一预编码矩阵v1，使用检测到的发射码流替换所述将n值加1，若n的值不等于β，则返回步骤s32进行迭代运算，若n的值等于β，将得到的u″作为第二合并矩阵u2，将得到的v″作为第二预编码矩阵v2。

其中，初始化发射端的预编码矩阵为随机酉矩阵。

其中，步骤s12具体为：

步骤s13具体为：

其中，k为对称mimo干扰系统发射端和接收端的个数，hi,j为从发射端j到接收端i的信道矩阵；vi为发射端i的预编码矩阵；orth{a}表示对矩阵a进行正交化处理，变量为信噪比，为通信链路的反向链路的信道矩阵。

其中，步骤s2具体为：

其中，步骤s32具体为：

步骤s33具体为：

其中，步骤s4具体为：

与现有技术相比，本发明采用传统的迭代方法进行了第一步的计算，而在第二步迭代中将符号检测考虑进去，也就是边检测边将检测到的符号引入到迭代计算中，通过这种方法，有效提高了mmse干扰对齐的性能，降低误码率，在高信噪比区域增益明显。

附图说明

图1为本发明基于符号检测的干扰对齐方法的示意图；

图2为本发明与现有技术在均方误差的概率密度函数仿真图；

图3为本发明与现有技术随迭代次数增加的均方误差仿真图；

图4为本发明当α为100时，β取值变化时均方误差仿真图；

图5为本发明与现有技术在不同信噪比下符号检错率ser的仿真结果图。

具体实施方式

下面结合附图对本发明做进一步的说明。

图1示出了本发明提出的基于符号检测的mmse干扰对齐方法的流程图。本发明假设了一个对称的mimo干扰系统，有k个发射端，k个接收端，每个发射端发射的信号对于其中一个接收端是有用信号，而对其他接收端来说则为干扰信号，则第i个接收端接收到的信号可表示为

其中yi为接收到的信号；hi,j为从发射端j到接收端i的信道矩阵；vi为发射端i的预编码矩阵；si为发射码流向量；ni为接收端噪声向量，噪声均值为0、方差为σ²。

接收端通过合并矩阵ui的共轭转置对接收到的信号向量yi进行迫零处理，从而合并后的接收信号(判决码流)为

mmse干扰对齐算法的核心思想就是通过将发射码流和合并后的码流的均方误差最小化得到，即通过下面的式子求矩阵ui

其中tr[.]为求矩阵的迹，定义矩阵函数为

此时最优的矩阵ui由函数导数为零时的统计均值给出，即由均值条件给出如下

在该通信链路的反向链路的信道矩阵并将ui和vi分别用作预编码矩阵和迫零合并矩阵，则可以得出最优的vi为

实际迭代计算中，为了在计算中消除未知的码流sj的影响，首先，在计算ui和vi的过程中采取了对sj取统计平均的处理，即有

其中p为码流发射功率。

此时，最优的ui和vi由下式给出

在按照公式(8)和(9)迭代α-β次之后，获得了最优的ui和vi。

之后，按照公式(2)计算获得发射端的码流。

之后，在公式(5)-(6)中替换码流向量后得到如下公式

按照公式(10)和(11)迭代β次之后，获得了基于符号检测的最优的ui和vi。

之后，使用公式(2)计算获得发射端的码流，获得最终的发射端码流。

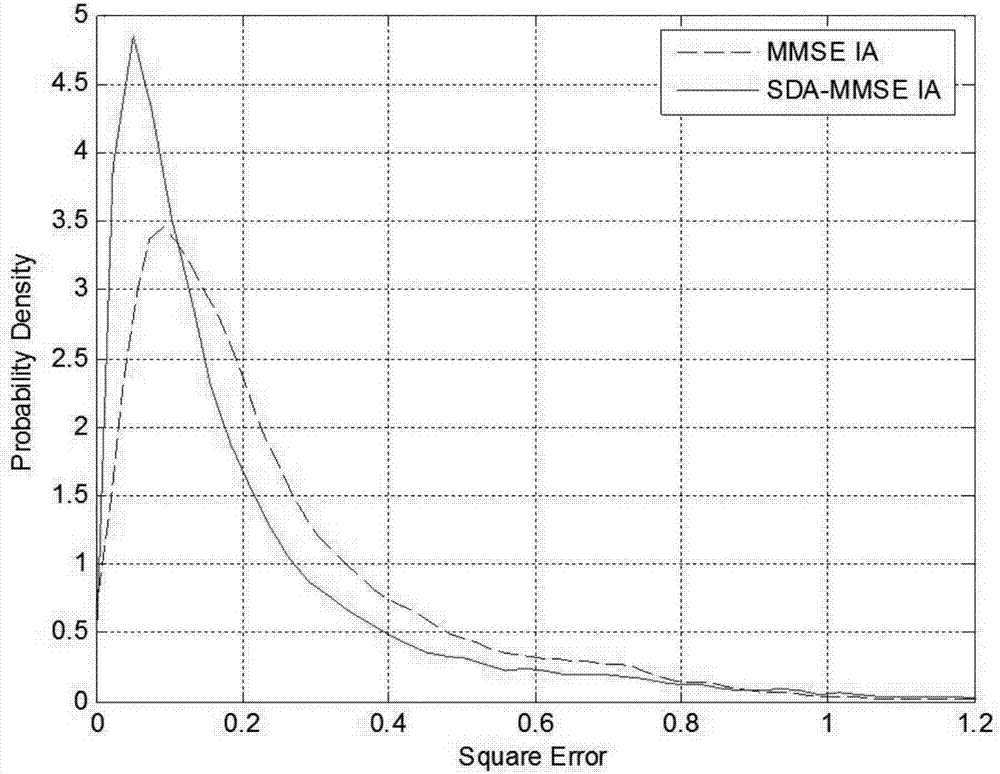
图2为传统方法(mmseia)和本方法所提出的新方法(symbol-detection-aided-mmseia，sda-mmseia)在均方误差的概率密度函数结果，从中可以看出所提方法的均方误差更多的分布在较低区域。

图3为传统方法和本发明所提出的新方法的均方误差在随着迭代次数α增加而变化的结果，从中可以看出，不管变量α如何增加，所提新方法具有更低的均方误差。

为了更好的设置α和β的值，以使其能够获得最优的性能，本发明假设一个3用户对称干扰mimo信道，其中每个发射端为4天线发送2个独立码流、接收端为4天线接收，调制方式为qpsk，迭代次数α＝100。

对于一个固定的α其对应的最佳参数β可以通过仿真得出，在不同网络参数配置下其最优值不一样。从图4可以看出α＝100时最优的β＝7。

图5给出了传统方法和本发明所提出的新方法在不同信噪比下的符号检测错误率ser的仿真结果。从图中不难看出，所提方法优于传统方法，尤其是在高信噪比区域增益最为明显。

尽管前面公开的内容示出了本公开的示例性实施例，但是应当注意，在不背离权利要求限定的本公开的范围的前提下，可以进行多种改变和修改。

以上所述的具体实施方式，对本公开的目的、技术方案和有益效果进行了进一步详细说明，所应理解的是，以上所述仅为本公开的具体实施方式而已，并不用于限定本公开的保护范围，凡在本公开的精神和原则之内，所做的任何修改、等同替换、改进等，均应包含在本公开的保护范围之内。