一种基于贝叶斯估计和种子节点邻居集合的链路预测方法与流程

本发明涉及网络科学和链路预测领域，特别是指一种基于贝叶斯估计和种子节点邻居集合的链路预测方法。

背景技术：

现实生活中的复杂系统可以使用复杂网络进行研究，网络中的节点代表复杂系统中的个体，连边代表系统中节点之间的相互关系。链路预测是复杂网络的重要研究领域之一，因为链路预测可以对网络的演化过程中节点之间可能产生的链路进行预测，所有可以提前预判出网络的演化趋势，并且可以判断出网络中并不存在的“幽灵边”，能够更好的帮助研究人员研究网络的内在规律。

链路预测问题受到研究人员的广泛关注。相比较而言，基于网络结构的链路预测算法相对于基于网络节点属性信息的预测算法更加可靠、准确。共同邻居(cn)算法是一种基于网络结构的经典链路预测算法，这种算法又被称为结构等价算法，即节点之间有很多的共同邻居节点，那么这两个节点就越相似，在cn算法的基础之上衍生出的链路预测算法有salton算法、jaccard算法、sorenson算法、hpi(大度节点有利指标)、hdi(大度节点不利指标)、lhn-i算法、aa算法和ra算法等等，其中salton算法又被称为余弦相似性算法，sorenson算法常被用于生态学数据的研究，hpi算法常被用来分析新陈代谢网络的拓扑相似性，aa算法的思想是度小的共同邻居节点的贡献大于度大的共同邻居节点，ra算法是在aa算法的基础之上，受资源分配过程的启发而提出来的；基于路径的相似性算法，主要包括了局部路径指标(localpath，lp)、katz算法lhn-ii算法，这些算法克服了cn算法使用的网络有效信息过少的缺点，从全局的角度利用网络的有效信息，因此，一定程度上提高了链路预测的精确性。

上述的一些经典算法主要考虑的是网络中的拓扑结构特性，即两个节点之间的网络特征越相似，那么这两个节点之间越有可能产生链路，这些方法在很多网络中的仿真被证实是有效的，但是这些传统的经典算法大部分只考虑了没有直接连边的节点对之间长度为二的路径的中间节点的度数信息，并没有考虑长度大于二的路径的中间节点的属性，事实上网络中的这些属性对于节点对之间产生链路有很大的作用。传统的基于种子节点邻居集合的链路预测算法只是考虑了种子节点之间路径长度等于2的路径的中间节点，而且只是统计了这些长度为2的路径的中间节点，对这些节点并没有作出区分，所以无法区分这些中间节点的重要性。

技术实现要素：

为了克服现有的基于种子节点邻居集合的链路预测方法只考虑路径长度等于2和3的路径的中间节点，并且，只考虑这些节点的度数而导致的预测精度不高的不足，本发明提出了一种准确度较高的基于贝叶斯估计和种子节点邻居集合的链路预测方法。

本发明解决其技术问题所采用的技术方案是：

一种基于贝叶斯估计和种子节点邻居集合的链路预测方法，包括以下步骤：

步骤一：建立网络模型g(v,e)，v代表网络中的节点集合，e代表网络中的连边集合，网络的节点总数记为n,用u表示网络中节点对的集合，|u|＝n(n-1)/2表示网络中节点对的总数；

步骤二：任意选取网络中的两个节点x和y作为种子节点，计算它们之间存在直接连边的可能性：

其中，|e|表示网络中实际存在的连边总数，a1表示x和y两个节点之间存在直接连边；

步骤三：计算网络中任意两个节点x和y之间不存在直接连边的概率：

其中，a0表示x和y两个节点之间不存在直接连边；

步骤四：根据节点x和y之间长度为2或者3的路径的一个中间节点vw的度信息，计算节点x和y之间产生连边的概率：

p(a1|vw)＝cw

其中，cw＝2ew/kw(kw-1),kw表示节点vw的度数，ew表示节点vw的kw个邻居节点之间实际存在的边数；

步骤五：根据节点x和y之间长度为2或者3的路径的一个中间节点vw的度信息，计算节点x和y之间不产生连边的概率：

p(a0|vw)＝1-cw；

步骤六：根据贝叶斯估计的方法，计算节点x和y之间长度为2和3的路径的任意一个中间节点vw的似然值

步骤七：对节点x和y之间长度为2和3的路径的每一个中间节点，重复步骤四至步骤六，计算每一个中间节点的似然值

步骤八：计算节点x和y的相似性分数：

其中q表示节点x和y之间长度为2和3的所有路径的中间节点的数量，mx表示节点x的一阶和二阶邻居数量之和，x的一阶邻居指的是和x距离为1的节点，x的二阶邻居指的是和x距离为2的节点；my表示节点y的一阶和二阶邻居数量之和；

步骤九：遍历整个网络，对任意两个未连接节点，重复步骤二至步骤八，计算所有未连接节点对之间的相似性分数，并按照相似性分数值从高到低排列顺序，取前b个相似性分数值对应的节点对为预测连边，其中，b为设定的一个正整数，b≤d，d为网络中所有未连接节点对的数量。

本发明的有益效果为：考虑网络中两个未连接节点之间路径长度等于2或3的局部路径，区分网络中的中间节点的度数对产生链路的贡献，提出了一种基于贝叶斯估计和种子节点邻居集合的链路预测方法，链路预测准确度较高。

附图说明

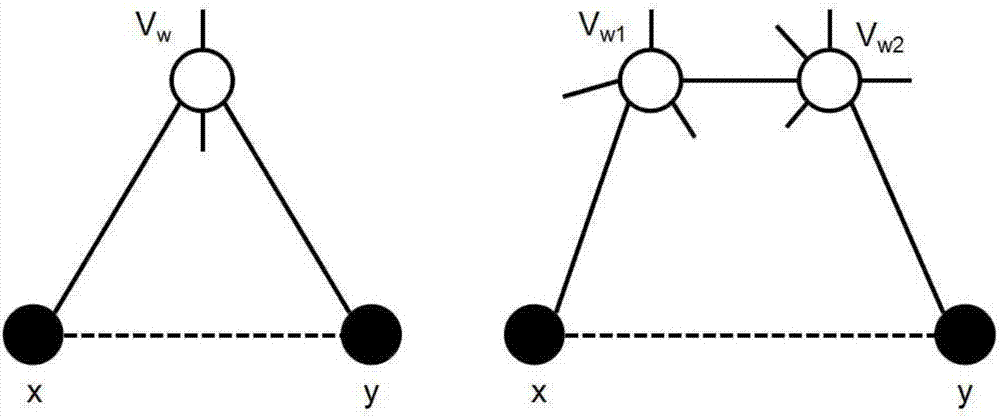
图1为网络中的任意一个不存在直接连边的节点对之间的不同中间节点对这个节点对之间产生链路的影响。

具体实施方式

下面结合附图对本发明做进一步说明。

参照图1，一种基于贝叶斯估计和种子节点邻居集合的链路预测方法，包括以下步骤：

步骤一：建立网络模型g(v,e)，v代表网络中的节点集合，e代表网络中的连边集合，网络的节点总数记为n,用u表示网络中节点对的集合，|u|＝n(n-1)/2表示网络中节点对的总数；

步骤二：任意选取网络中的两个节点x和y作为种子节点，即图1中黑色圆点表示，计算它们之间存在直接连边的可能性：

其中，|e|表示网络中实际存在的连边总数，a1表示x和y两个节点之间存在直接连边；

步骤三：计算网络中任意两个节点x和y之间不存在直接连边的概率，如图1所示：

其中，a0表示x和y两个节点之间不存在直接连边；

步骤四：根据节点x和y之间长度为2或者3的路径的一个中间节点vw(如图1所示)的度信息，计算节点x和y之间产生连边的概率：

p(a1|vw)＝cw

其中，cw＝2ew/kw(kw-1),kw表示节点vw的度数，ew表示节点vw的kw个邻居节点之间实际存在的边数；

步骤五：根据节点x和y之间长度为2或者3的路径的一个中间节点vw(如图1所示)的度信息，计算节点x和y之间不产生连边的概率：

p(a0|vw)＝1-cw；

步骤六：根据贝叶斯估计的方法，计算节点x和y之间长度为2和3的路径的任意一个中间节点vw的似然值

步骤七：对节点x和y之间长度为2和3的路径的每一个中间节点，重复步骤四至步骤六，计算每一个中间节点的似然值

步骤八：计算节点x和y的相似性分数：

其中q表示节点x和y之间长度为2和3的所有路径的中间节点的数量，mx表示节点x的一阶和二阶邻居数量之和，x的一阶邻居指的是和x距离为1的节点，x的二阶邻居指的是和x距离为2的节点；my表示节点y的一阶和二阶邻居数量之和；

步骤九：遍历整个网络，对任意两个未连接节点，重复步骤二至步骤八，计算所有未连接节点对之间的相似性分数，并按照相似性分数值从高到低排列顺序，取前b个相似性分数值对应的节点对为预测连边，其中，b为设定的一个正整数，b≤d，d为网络中所有未连接节点对的数量。

如上所述，本专利实施的具体实现步骤使本发明更加清晰。在本发明的精神和权利要求的保护范围内，对本发明作出的任何修改和改变，都落入本发明的保护范围。