一种RSA加解密处理方法和装置与流程

本申请涉及数据加密领域，尤其涉及一种rsa加解密处理方法和装置。

背景技术：

rsa算法是1977年由罗纳德·李维斯特(ronrivest)、阿迪·萨莫尔(adishamir)和伦纳德·阿德曼(leonardadleman)一起提出的。1987年首次公布，当时他们三人都在麻省理工学院工作。rsa就是他们三人姓氏开头字母拼在一起组成的。

rsa算法是目前最有影响力的公钥加密算法，它能够抵抗到目前为止已知的绝大多数密码攻击，已被iso推荐为公钥数据加密标准。

rsa算法基于一个十分简单的数论事实：将两个大质数相乘十分容易，但是想要对其乘积进行因式分解却极其困难，因此可以将乘积公开作为加密密钥。

处理rsa算法的传统方式是通过软件来处理。但是通过软件处理rsa算法，在加解密过程中，运算量非常大，需要加大芯片级系统soc(systemonchip)的ram空间才能通过软件处理rsa算法。而且通过软件处理rsa算法，其运算速率较慢，在系统时钟较慢的soc上，通过软件处理rsa算法一般无法在规定的时间内完成运算。替代地，采用硬件电路处理rsa算法可以大大提升rsa算法的运算速率。

用硬件电路处理rsa算法，其核心是需要根据c＝m^emodn运算生成密文，根据m＝c^dmodn运算生成明文，式中，c为密文，m为明文，(e,n)为rsa公钥，(d,n)为rsa密钥。

现有的利用硬件电路处理rsa算法的方法中，运算明文和密文的方式是先直接求出乘幂，然后再求出乘幂对n的模，但是，这种运算方式由于要进行模幂运算，运算量非常大，尤其是当m、n为比较大的数值时，用硬件电路实现需要占用大量的硬件资源，而且运算耗时非常长，无法在规定的时间内利用有限的硬件资源处理完rsa算法。

技术实现要素：

有鉴于此，本申请提供了一种rsa加解密处理方法和装置，以减少rsa加解密过程中的运算量，实现rsa算法在规定的时间内利用有限的硬件资源处理完成。

为了解决上述技术问题，本申请采用了如下技术方案：

一种rsa加密处理方法，包括：

获取rsa公钥以及明文m，所述rsa公钥为e和n；

判断e是否大于0；

当e大于0时，判断e是否为偶数；

当e为偶数时，更新e值以及通过模乘运算更新明文m，其中，e＝e/2，m＝m*mmodn；返回执行所述判断e是否大于0的步骤；

当e为奇数时，更新e值以及通过模乘运算更新第一中间变量d，其中，e＝e-1，d＝d*mmodn，返回执行所述判断e是否大于0的步骤；设定d的初始值等于1；

当e＝0时，输出第一中间变量d值，输出的d值为rsa密文；

其中，所述模乘运算包括：乘运算和对所述乘运算的乘积采用移位相减的方式进行取模运算。

可选地，设定所述乘运算的乘积为x，所述对所述乘运算的乘积采用移位相减的方式进行取模运算，具体包括：

将n向左移位，判断左移位后的n的位宽与x位宽的差值是否在预设范围内，直到左移位后的n的位宽与x的位宽的差值在预设范围内；

比较x和n的大小关系，当x大于n时，通过x＝x-n的减法运算更新x，并将n逐位向右移位，直到右移后的n的值恢复到左移之前的n的初始值，将最后一次更新后的x值确定为取模结果。

可选地，所述将n向左移位，判断左移位后的n的位宽与x位宽的差值是否在预设范围内，直到左移位后的n的位宽与x的位宽的差值在预设范围内，具体包括：

设定一第二中间变量a，并且设定a的初始值等于n，即a＝n；

判断x是否大于或等于2a；

当x≥2a时，将a左移一位，即a＝2a，返回执行所述判断x是否大于或等于2a的步骤，直至x<2a。

可选地，所述比较x和n的大小关系，当x大于n时，通过x＝x-n的减法运算更新x，并将n按位向右移位，直到n的值恢复到左移之前的n的初始值，将最后更新后的x值确定为取模结果，具体包括：

当x<2a时，判断x是否大于或等于a；

当x≥a时，更新x和a的值，其中，x＝x-a，a＝a/2；

判断a是否等于n；

当a＝n时，输出x值，x值作为取模结果，结束取模运算；

当a不等于n时，返回执行判断x是否大于或等于a的步骤；

当x<a时，更新a的值，其中，设定a＝a/2，返回执行判断a是否等于n。

一种rsa加密处理装置，包括：

输入单元，用于输入rsa公钥以及明文m，所述rsa公钥为e和n；

第一判断单元，用于判断e是否大于0；

第二判断单元，用于当e大于0时，判断e是否为偶数；

第一更新单元，用于当e为偶数时，更新e值，并触发所述第一判断单元，其中，e＝e/2；

第一模乘运算单元，用于当e为偶数时，通过模乘运算更新明文m，m＝m*mmodn；

第二更新单元，用于当e为奇数时，更新e值，并触发所述第一判断单元，其中，e＝e-1；

第二模乘运算单元，用于当e为奇数时，更新第一中间变量d，并触发所述第一判断单元，其中，d＝d*mmodn，d的初始值等于1；

输出单元，用于当e＝0时，输出第一中间变量d值，输出的d值为rsa密文；

其中，所述第一模乘运算单元和/或所述第二模乘运算单元均分别包括：乘运算子单元和对所述乘运算的乘积采用移位相减的方式进行取模运算的取模运算子单元。

可选地，所述取模运算子单元包括：

左移位子单元，用于将n向左移位；

判断子单元，用于判断左移位后的n的位宽与x位宽的差值是否在预设范围内，若判断结果为否，触发所述左移位子单元，直到左移位后的n的位宽与x的位宽的差值在预设范围内；

比较子单元，用于若判断结果为是，比较x和n的大小关系；

减法运算子单元，用于当x>n时，通过x＝x-n的减法运算更新x；

右移位子单元，用于当x>n时，将n逐位向右移位，并触发所述比较子单元，直到右移后的n值恢复到左移之前的n的初始值；

确定子单元，用于当右移后的n值恢复到左移之前的n的初始值时，将最后一次更新后的x值确定为取模结果。

一种rsa解密处理方法，包括：

获取rsa私钥以及密文c，所述rsa私钥为d和n；

判断d是否大于0；

当d大于0时，判断d是否为偶数；

当d为偶数时，更新d值以及通过模乘运算更新密文c，其中，d＝d/2，c＝c*cmodn；返回执行所述判断d是否大于0的步骤；

当d为奇数时，更新d值以及通过模乘运算更新第二中间变量d’，其中，d＝d-1，d'＝d'*cmodn，返回执行所述判断d是否大于0的步骤；设定d’的初始值等于1；

当d＝0时，输出第二中间变量d’值，输出的d’值为rsa明文；

其中，所述模乘运算包括：乘运算和对所述乘运算的乘积采用移位相减的方式进行取模运算。

可选地，设定所述乘运算的乘积为x’，所述对所述乘运算的乘积采用移位相减的方式进行取模运算，具体包括：

将n向左移位，判断左移位后的n的位宽与x’位宽的差值是否在预设范围内，直到左移位后的n的位宽与x’的位宽的差值在预设范围内；

比较x’和n的大小关系，当x’大于n时，通过x’＝x’-n的减法运算更新x’，并将n逐位向右移位，直到右移后的n的值恢复到左移之前的n的初始值，将最后一次更新后的x’值确定为取模结果。

一种rsa解密处理装置，包括：

获取单元，用于获取rsa私钥以及密文c，所述rsa私钥为d和n；

第一判断单元，用于判断d是否大于0；

第二判断单元，用于当d大于0时，判断d是否为偶数；

第一更新单元，用于当d为偶数时，更新d值并触发所述第一判断单元，其中，d＝d/2；

第一模乘运算单元，用于通过模乘运算更新密文c，并触发所述第一判断单元，其中，c＝c*cmodn；

第二更新单元，用于当d为奇数时，更新d值并触发所述第一判断单元，其中，d＝d-1；

第二模乘运算单元，用于当d为奇数时，通过模乘运算更新第二中间变量d’，并触发所述第一判断单元，其中，d'＝d'*cmodn，设定d’的初始值等于1；

输出单元，用于当d＝0时，输出第二中间变量d’值，输出的d’值为rsa明文；

其中，所述第一模乘运算单元和/或所述第二模乘运算单元均分别包括：乘运算子单元和对所述乘运算的乘积采用移位相减的方式进行取模运算的取模运算子单元。

可选地，所述取模运算子单元包括：

左移位子单元，用于将n向左移位；

判断子单元，用于判断左移位后的n的位宽与x’位宽的差值是否在预设范围内，若判断结果为否，触发所述左移位子单元，直到左移位后的n的位宽与x’的位宽的差值在预设范围内；

比较子单元，用于若判断结果为是，比较x’和n的大小关系；

减法运算子单元，用于当x’>n时，通过x’＝x’-n的减法运算更新x’；

右移位子单元，用于当x’>n时，将n逐位向右移位，并触发所述比较子单元，直到右移后的n值恢复到左移之前的n的初始值；

确定子单元，用于当右移后的n值恢复到左移之前的n的初始值时，将最后一次更新后的x’值确定为取模结果。

相较于现有技术，本申请具有以下有益效果：

本申请提供的rsa加解密处理方法中，无需直接计算乘幂，而是将密文和明文计算公式中的乘幂逐步化简为模乘运算，并且对每步模乘运算均采用移位相减的取模方法对乘积进行取模运算，将对最后一步化简到的模乘运算进行取模运算得到的取模结果作为rsa密文和明文。

在本申请提供的rsa加解密处理方法中，在取模运算过程中，通过左移位的方法将n的位宽与乘积的位宽的差值缩小到预设范围内，再采用减法运算以及右移位的方法进行取模运算，该取模运算过程运算量较小，耗时较短，如此提高了rsa加解密过程的处理速率，缩短了运算时间，从而使得rsa算法能够在规定的时间内利用有限的硬件资源处理完成。

附图说明

为了清楚地理解本申请的具体实施方式，下面将描述本申请具体实施方式时用到的附图做一简要说明。显而易见地，这些附图仅是本申请的部分实施例。

图1是本申请实施例提供的rsa加密处理方法流程示意图；

图2是本申请实施例提供的取模运算实现方式的流程示意图；

图3是本申请实施例提供的rsa加密处理方法的一个示例的流程示意图；

图4是本申请实施例提供的rsa加密处理装置结构示意图；

图5是本申请实施例提供的取模运算子单元的结构示意图；

图6是本申请实施例提供的rsa解密处理方法流程示意图；

图7是本申请实施例提供的取模运算实现方式的流程示意图；

图8是本申请实施例提供的rsa解密处理装置结构示意图。

具体实施方式

为了减少rsa加解密过程中的运算量，实现rsa算法在规定的时间内利用有限的硬件资源处理完成，本申请提供的rsa加解密处理方法中，将生成加密明文的计算公式c＝m^emodn和生成解密明文的计算公式m＝c^dmodn中的模幂运算逐步化简为模乘运算，然后对每步化简的模乘运算利用移位相减的方法进行取模运算，直到消掉模幂运算中的幂运算。在取模运算过程中，通过左移位的方法将n的位宽与乘积的位宽的差值缩小到预设范围内，再采用减法运算以及右移位的方法进行取模运算，该取模运算过程运算量较小，耗时较短，如此提高了rsa加解密过程的处理速率，缩短了运算时间，从而使得rsa算法能够在规定的时间内利用有限的硬件资源处理完成。

下面结合附图对本申请的具体实施方式进行详细描述。

图1是本申请实施例提供的rsa加密处理方法流程示意图。如图1所示，该生成方法包括以下步骤：

s101、获取rsa公钥(e，n)以及明文m。

为了提高安全性，公钥e和n的数值较大。在rsa算法应用过程中，n的值位宽一般都在512比特以上。

s102、判断e是否大于0。

s103、当e大于0时，判断e是否为偶数。

s104、当e为偶数时，更新e值以及通过模乘运算更新明文m，其中，e＝e/2，m＝m*mmodn；返回执行步骤s102；

s105、当e为奇数时，更新e值以及通过模乘运算更新第一中间变量d，其中，e＝e-1，d＝d*mmodn，返回执行步骤s102；设定d的初始值等于1；

s106、当e＝0时，输出第一中间变量d值，输出的d值为rsa密文。

其中，所述模乘运算可以具体包括：首先进行乘运算得到乘积x，然后再对乘积x采用移位相减的方式进行取模运算。

其中，乘运算比较简单，采用本领域管用的技术手段即可。

然而，取模运算的常规运算方式一般是通过试商的方法来实现。例如在计算xmodn时，首先比较x与n的大小关系，当x≥n时，更新x值，其中，x＝x-n，返回执行所述判断x是否大于n；当x<n时，将x作为数据x对n的模。也就是说，采用试商的方法计算xmodn时，如果x≥n，设定x＝x-n，一直循环减下去，直至x<n为止。这种取模运算方法在x和n的位宽较小的时候很实用，而且很方便，但是，如果x和n的位宽都很大的情况下，这种运算方式就非常地耗时，很难满足rsa算法时间要求。

为了提高取模运算的运算效率，使得rsa算法在规定时间内完成，本申请可以采用移位相减的方法对所述乘积x进行取模运算得到取模结果。

采用移位相减的方法对乘积x进行取模运算得到取模结果可以具体包括以下步骤：

步骤a：将n向左移位，判断左移位后的n的位宽与x位宽的差值是否在预设范围内，直到左移位后的n的位宽与x的位宽的差值在预设范围内；

步骤b：比较x和n的大小关系，当x大于n时，通过x＝x-n的减法运算更新x，并将n逐位向右移位，直到右移后的n的值恢复到左移之前的n的初始值，将最后一次更新后的x值确定为取模结果。

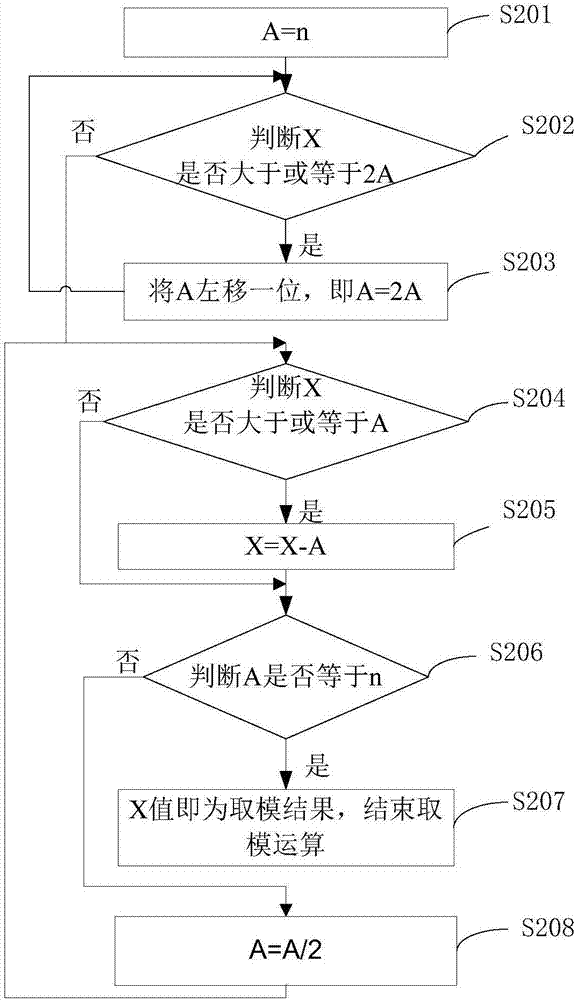
作为示例，采用移位相减的方法对所述乘积x进行取模运算得到取模结果的具体实现方式如图2所示，其包括以下步骤：

s201、设定一中间变量a，并且设定a的初始值等于n，即a＝n。

s202、判断x是否大于或等于2a，如果是，执行步骤s203，如果否，执行步骤s204。

s203、将a左移一位，即a＝2a，返回执行步骤s202。

在计算机中，数值一般是以二进制的形式存在。在本申请实施例中，将中间变量a整体向左移动一位，并在最后一位上补0。作为示例，以中间变量a为1101b为例说明。将a左移一位，更新后的a为11010b。

s204、判断x是否大于或等于a，如果是，执行步骤s205，如果否，执行步骤s206。

s205、当x≥a时，更新x的值，其中，x＝x-a。

s206、判断a是否等于n，如果是，执行步骤s207，如果否，返回执行步骤s208。

s207、当a＝n时，x值即为取模结果，结束取模运算；

s208、当a≠n时，更新a的值，更新a值具体通过将a右移一位，即a＝a/2实现，返回执行步骤s204。

以上为本申请实施例提供的移位相减的取模运算方法的具体实施方式。

其中，步骤s201至s203为上述步骤a的一种可能的具体实现方式。步骤s204至s208为上述步骤b的一种可能的具体实现方式。

通过该具体实施方式，能够将取模运算转换为较少的减法运算，从而大大降低了取模运算的复杂度，进而能够利用有限的硬件资源在规定的时间内处理完成rsa加密算法。

为了更清楚地理解本申请提供的rsa加密处理方法的具体实施方式，下面以e＝4为例说明本申请提供的rsa加密处理方法的具体实现方式，该示例的实现过程可以如图3所示，其包括以下步骤：

s301、初始化中间变量d的值，设定d的初始值等于1。

s302、获取rsa公钥(e，n)以及明文m。

s303、判断4是否大于0，如果是，执行步骤s304。

根据数学基础知识可知4>0，判断结果为是，因此，执行步骤s304。

s304、判断4是否为偶数，如果是，执行步骤s305。

根据数学基础知识可知，4为偶数，判断结果为是，所以，执行步骤s305。

s305、更新e值以及通过模乘运算更新m值，其中，e＝e/2＝4/2＝2，m＝m*mmodn。

在本申请实施例中，通过模乘运算更新m值，具体可以如下：先计算模乘运算m*mmodn中的乘运算m*m，得到乘积a；再利用移位相减的取模运算方式对所述乘积a进行取模运算得到取模结果，得到的取模结果即为更新后的m值。

s306、判断2是否大于0，如果是，执行步骤s307。

根据数学基础知识可知，2>0，判断结果为是，执行步骤s307。

s307、判断2是否为偶数，如果是，执行步骤s308。

根据数学基础知识可知，2为偶数，判断结果为是，执行步骤s308。

s308、更新e值以及通过模乘运算更新m值，其中，e＝e/2＝2/2＝1，m＝m*mmodn。

s309、判断1是否大于0，如果是，执行步骤s310。

根据数学基础知识可知，1>0，判断结果为是，执行步骤s310。

s310、判断1是否为偶数，判断结果为否，执行步骤s311。

根据数学基础知识可知，1为奇数，判断结果为否，执行步骤s311。

s311、更新e值以及通过模乘运算更新d值，其中，e＝e-1＝1-1＝0，d＝d*mmodn＝1*mmodn＝mmodn。

在本申请实施例中，通过模乘运算更新d值，具体可以如下：先计算模乘运算d*mmodn中的乘运算d*m，得到乘积b；然后再对所述乘积b进行取模运算得到取模结果，得到的取模结果即为更新后的d值。

s312、判断0是否大于0，如果否，执行步骤s313。

根据数学基础知识可知，0＝0，判断结果为否，执行步骤s313。

s313、输出d值，输出的d值作为rsa加密密文，然后结束运算。

以上为本申请实施例提供的rsa加密处理方法的具体实施方式，在本申请提供的rsa加密处理方法中，无需计算乘幂，而是将密文计算公式中的乘幂逐步化简为模乘运算，并且对每步模乘运算均采用移位相减的取模方法对乘积进行取模运算，将对最后一步化简到的模乘运算进行模运算得到的取模结果作为rsa密文。在取模运算过程中，通过左移位的方法将n的位宽与乘积的位宽的差值缩小到预设范围内，再采用减法运算以及右移位的方法进行取模运算，该取模运算过程运算量较小，耗时较短，如此提高了rsa加密过程的处理速率，缩短了运算时间，从而使得rsa算法能够在规定的时间内利用有限的硬件资源处理完成。

通过验证用硬件处理rsa加密算法，在e位宽为24比特，n位宽为1024比特的情况下，模乘运算用0.13μm工艺综合之后面积为49万平方微米，考虑到最差的情况，计算一次m^emodn(m取最大值，e取最大值，n取最小值2)需要时间为(2048+4)*256*24＝12,607,488个时钟周期，如果采用30mhz的系统时钟最差的情况需要0.4s，可以满足绝大部分rsa算法的时间要求。因而，通过该方法，可以用很少的数字逻辑面积并且可以保持较快的运算速率，因此，该方法解决了通过硬件实现rsa算法需要占用大量的硬件资源而且运算耗时非常长的问题。

以上为本申请实施例提供的rsa加密处理方法的具体实施方式。基于上述实施例提供的rsa加密处理方法的具体实施方式，本申请实施例还提供了rsa加密处理装置的具体实施方式。图4是本申请实施例提供的rsa加密处理装置结构示意图。如图4所示，该rsa加密处理装置包括：

输入单元41，用于输入rsa公钥以及明文m，所述rsa公钥为e和n；

第一判断单元42，用于判断e是否大于0；

第二判断单元43，用于当e大于0时，判断e是否为偶数；

第一更新单元44，用于当e为偶数时，更新e值。并触发所述第一判断单元，其中，e＝e/2；

第一模乘运算单元45，用于当e为偶数时，通过模乘运算更新明文m，m＝m*mmodn；

第二更新单元46，用于当e为奇数时，更新e值，并触发所述第一判断单元，其中，e＝e-1；

第二模乘运算单元47，用于当e为奇数时，更新第一中间变量d，并触发所述第一判断单元，其中，d＝d*mmodn，d的初始值等于1；

输出单元48，用于当e＝0时，输出第一中间变量d值，输出的d值为rsa密文；

其中，所述第一模乘运算单元45和/或所述第二模乘运算单元47均分别包括：乘运算子单元和对所述乘运算的乘积采用移位相减的方式进行取模运算的取模运算子单元。

其中，如图5所示，取模运算子单元可以具体包括：

左移位子单元51，用于将n向左移位；

判断子单元52，用于判断左移位后的n的位宽与x位宽的差值是否在预设范围内，若判断结果为否，触发所述左移位子单元51，直到左移位后的n的位宽与x的位宽的差值在预设范围内；

比较子单元53，用于若判断结果为是，比较x和n的大小关系；

减法运算子单元54，用于当x>n时，通过x＝x-n的减法运算更新x；

右移位子单元55，用于当x>n时，将n逐位向右移位，并触发所述比较子单元，直到右移后的n值恢复到左移之前的n的初始值；

确定子单元56，用于当右移后的n值恢复到左移之前的n的初始值时，将最后一次更新后的x值确定为取模结果。

需要说明，本申请实施例提供的rsa加密处理装置可以为由硬件电路组成的装置。其中，输入单元41和输出单元48可以为数据输入/输出接口。第一判断42和第二判断单元43可以为比较器。第一模乘运算单元45和第二模乘运算单元47可以为模乘运算器。作为一示例，第一模乘运算单元45和第二模乘运算单元47可以为同一模乘运算单元，该模乘运算单元对不同的输入数据进行模乘运算。本申请实施例提供的rsa加密处理装置能够大大降低rsa加密处理过程所需的运算时间。

基于与rsa加密处理方法相同的工作原理，本申请还提供了rsa解密处理方法的具体实施方式。具体参见以下实施例。

图6是本申请实施例提供的一种rsa解密处理方法流程示意图。如图6所示，该rsa解密处理方法包括：

s601、获取rsa私钥以及密文c，所述rsa私钥为d和n。

s602、判断d是否大于0。

s603、当d大于0时，判断d是否为偶数。

s604、当d为偶数时，更新d值以及通过模乘运算更新密文c，其中，d＝d/2，c＝c*cmodn'；返回执行步骤s602。

s605、当d为奇数时，更新d值以及通过模乘运算更新第二中间变量d’，其中，d＝d-1，d'＝d'*cmodn'，返回执行步骤s602；设定d’的初始值等于1；

s606、当d＝0时，输出第二中间变量d’值，输出的d’值为rsa明文；

其中，所述模乘运算包括：乘运算和对所述乘运算的乘积采用移位相减的方式进行取模运算。

其中，所述模乘运算可以具体包括：首先进行乘运算得到乘积x’，然后再对乘积x’采用移位相减的方式进行取模运算。

为了提高取模运算的运算效率，使得rsa算法在规定时间内完成，本申请可以采用移位相减的方法对所述乘积x’对n进行取模运算得到取模结果。

采用移位相减的方法对乘积x’对n进行取模运算得到取模结果可以具体包括以下步骤：

步骤a’：将n向左移位，判断左移位后的n的位宽与x’位宽的差值是否在预设范围内，直到左移位后的n的位宽与x’的位宽的差值在预设范围内；

步骤b’：比较x’和n的大小关系，当x’大于n时，通过x’＝x’-n的减法运算更新x’，并将n逐位向右移位，直到右移后的n的值恢复到左移之前的n的初始值，将最后一次更新后的x’值确定为取模结果。

作为示例，采用移位相减的方法对所述乘积x’进行取模运算得到取模结果的具体实现方式如图7所示，其包括以下步骤：

s701、设定一中间变量a，并且设定a的初始值等于n，即a＝n。

s702、判断x’是否大于或等于2a，如果是，执行步骤s703，如果否，执行步骤s704。

s703、将a左移一位，即a＝2a，返回执行步骤s702。

在计算机中，数值一般是以二进制的形式存在。在本申请实施例中，将中间变量a整体向左移动一位，并在最后一位上补0。作为示例，以中间变量a为1101b为例说明。将a左移一位，更新后的a为11010b。

s704、判断x’是否大于或等于a，如果是，执行步骤s705，如果否，执行步骤s706。

s705、当x’≥a时，更新x’和a的值，其中，x’＝x’-a。

s706、判断a是否等于n，如果是，执行步骤s707，如果否，返回执行步骤s708；

s707、当a＝n时，x’值即为取模结果，结束取模运算；

s708、当a≠n时，更新a的值，其中，设定a＝a/2，返回执行步骤s704。

其中，步骤s701至s703为上述步骤a’的一种可能的具体实现方式。步骤s704至s708为上述步骤b’的一种可能的具体实现方式。

需要说明，图7所示的取模运算过程与图2所示的取模运算过程相同，其不同之处仅在于数据不同。

以上为本申请实施例提供的rsa解密处理方法的具体实施方式，在本申请提供的rsa解密处理方法中，无需计算乘幂，而是将明文计算公式中的乘幂逐步化简为模乘运算，并且对每步模乘运算均采用移位相减的取模方法对乘积进行取模运算，将对最后一步化简到的模乘运算进行取模运算得到的取模结果作为rsa明文。在取模运算过程中，通过移位的方法将n的位宽与乘积的位宽的差值缩小到预设范围内，再采用减法运算以及右移位的方法进行取模运算，该取模运算过程运算量较小，耗时较短，如此提高了rsa解密过程的处理速率，缩短了运算时间，从而使得rsa算法能够在规定的时间内利用有限的硬件资源处理完成。

以上为本申请实施例提供的rsa解密处理方法的具体实施方式。基于上述实施例提供的rsa解密处理方法的具体实施方式，本申请实施例还提供了rsa解密处理装置的具体实施方式。图8是本申请实施例提供的rsa解密处理装置结构示意图。如图8所示，该rsa解密处理装置包括：

获取单元81，用于获取rsa私钥以及密文c，所述rsa私钥为d和n；

第一判断单元82，用于判断d是否大于0；

第二判断单元83，用于当d大于0时，判断d是否为偶数；

第一更新单元84，用于当d为偶数时，更新d值并触发所述第一判断单元，其中，d＝d/2；

第一模乘运算单元85，用于通过模乘运算更新密文c，并触发所述第一判断单元，其中，c＝c*cmodn；

第二更新单元86，用于当d为奇数时，更新d值并触发所述第一判断单元，其中，d＝d-1；

第二模乘运算单元87，用于当d为奇数时，通过模乘运算更新第二中间变量d’，并触发所述第一判断单元，其中，d'＝d'*cmodn，设定d’的初始值等于1；

输出单元88，用于当d＝0时，输出第二中间变量d’值，输出的d’值为rsa明文；

其中，所述第一模乘运算单元85和/或所述第二模乘运算单元88均分别包括：乘运算子单元和对所述乘运算的乘积采用移位相减的方式进行取模运算的取模运算子单元。

作为一具体示例，所述取模运算子单元包括：

左移位子单元，用于将n向左移位；

判断子单元，用于判断左移位后的n的位宽与x’位宽的差值是否在预设范围内，若判断结果为否，触发所述左移位子单元，直到左移位后的n的位宽与x’的位宽的差值在预设范围内；

比较子单元，用于若判断结果为是，比较x’和n的大小关系；

减法运算子单元，用于当x’>n时，通过x’＝x’-n的减法运算更新x’；

右移位子单元，用于当x’>n时，将n逐位向右移位，并触发所述比较子单元，直到右移后的n值恢复到左移之前的n的初始值；

确定子单元，用于当右移后的n值恢复到左移之前的n的初始值时，将最后一次更新后的x’值确定为取模结果。

需要说明，在本申请实施例中的取模运算子单元与上述rsa加密处理装置中的取模运算子单元的结构相同，其不同之处在于，本申请施例中的取模运算子单元是对乘积x’进行取模运算。

需要说明，本申请实施例提供的rsa解密处理装置可以为由硬件电路组成的装置。本申请实施例提供的rsa加密处理装置能够大大降低rsa加密处理过程所需的运算时间。

以上仅为本申请的实施例而已，并不用于限制本申请。对于本领域技术人员来说，本申请可以有各种更改和变化。凡在本申请的精神和原理之内所作的任何修改、等同替换、改进等，均应包含在本申请的权利要求范围之内。