自组织网络云计算中的任务卸载与功率分配联合决策方法与流程

本发明属于移动通信技术领域，特别涉及一种自组织网络adhoc云计算中的任务卸载与功率分配联合决策方法。

技术背景

在过去的三十年里，移动通信从语音业务到移动宽带数据业务得到了飞速发展，深深地改变着人们的生活水平和生活方式。随着制造工艺不断进步和制造成本不断降低，以智能手机为代表的移动设备快速普及，给人们的生活带来了极大的便利。而随着智能手机、平板等智能设备的不断推广，应用程序开发人员也已经把许多优秀的应用程序搬移到更加简便的移动设备上来，虽然智能终端的处理能力近年来不断提高，然而依然受到cpu性能、续航能力、储存容量等因素的限制，难以应对大数据时代各种数据的指数级增长，尤其是在处理一些计算密集型的任务时，更是表现欠佳，比如运算速度缓慢、掉电迅速等，使得智能移动终端在续航能力和响应速度上都远远低于普通pc机。

为了更好的为移动用户提供服务，移动云计算技术通过将本地计算任务卸载到云端或者本地微云的方式，扩展终端计算能力和移动设备的续航能力。

然而在有些场景中(如adhoc无线网络环境)没有可用的云基础设施或本地微云，不能保证移动终端可以随时随地的接入，或者由于服务器距离太远而造成较大的延迟和通信成本，进而造成资源任务卸载的失败。而adhoc云是一种无需任何预设网络设施的自组织云，具有部署快速和扩展灵活等特点，非常适合移动云计算环境下的任务卸载。在移动adhoc云中，各个移动设备通过adhoc网彼此共享它们的空闲资源，这一方式可以有效地缓解移动云计算中高延迟、低吞吐量等的瓶颈，另外，还可以提高终端设备的处理效率和续航能力。然而，由于计算任务迁移过程的复杂性，在adhoc云计算中依然存在很多问题亟待解决。比如，如何提高移动adhoc云计算环境中任务迁移效率；如何选择更加合适的计算代理；如何对移动设备有限的功率资源更加合理利用；如何控制任务卸载时延与能耗之间的关系等。另外，代理为客户端处理任务时，将会占用自身的处理空间，消耗自身的资源，在很多情况下，要求其他终端无偿提供帮助是不切实际的。

技术实现要素：

为了解决以上问题，本发明提供一种adhoc云计算中的任务卸载与功率分配联合决策方法。

本发明一种adhoc云计算中的任务卸载与功率分配联合决策方法，如图1所示；

s1、对移动终端进行划分，将在adhoc云网络中具有计算密集型任务的终端作为客户端，具有空闲资源的终端作为代理节点；

s2、定义客户端为买方、代理节点为卖方，利用买卖模型，分析买卖双方的行为并定义效用函数；

s3、以买卖双方最大化各自的收益效用为依据，分析得到买卖双方各自的最优解；

s4、客户端根据当前的网络环境选择为代理节点卸载多少计算任务，从而确定客户端自身功率分配策略。

优选地，步骤s2中买方收益效用为受到代理节点帮助卸载而带来的收益减去为向代理支付的任务卸载费用、任务提交过程的数据传输开销、系统传输时延惩罚及买方能耗开销。

优选地，步骤s2中卖方收益效用为买方向卖方支付的费用减去代理节点计算成本、代理节点结果返回的数据开销、卖方能耗开销。

优选地，步骤s3所述以买卖双方最大化各自的收益效用为依据，分析得到买卖双方各自的最优解包括寻求买方最优解获得买方最优任务卸载量及功率资源分配决策值。

优选地，根据买方最优解获得买方最优任务卸载量及功率资源分配决策值，寻求卖方最优解，获得卖方的最优价格决策值以及最优分配功率资源。

优选地，步骤s4所述客户端根据当前的网络环境选择为代理节点卸载多少计算任务，从而确定客户端自身功率分配策略，包括：客户端卸载任务量从0开始，代理节点报价从成本开始，根据wj^*＝f1(pij^*,vj,λ1^*)计算买方此时的卸载任务量wj和根据pij^*＝f2(wj^*,vj,λ2^*)计算功率资源分配决策值p^*ij，根据pji^*＝g2(wj^*,vj^*,φj^*)计算分配的功率pji^*，并带入vj^*＝g1(wj^*,pji^*,φj^*)，更新代理节点的报价，直到卖家报价收敛至最优，并以此得到最优的卖家发送功率，代理节点将此时的代理节点价格反馈给客户端；其中，wj^*表示买方卸载任务量，pij^*和pji^*表示最优功率资源分配决策值，vj^*表示卖方最优价格决策值，λ1^*和λ2^*是当得到w^*j和p^*ij的拉格朗日乘子，φj^*是当得到vj^*和pji^*的拉格朗日乘子。

本发明针对现有adhoc云计算中任务卸载算法的不足，以控制系统时延和能耗为基础，综合adhoc云计算环境中多属性决策问题，建立任务卸载与功率分配联合优化的理论分配模型，提出一种adhoc云计算中任务卸载与功率分配的分布式联合优化的激励机制。在均衡时延及能耗的基础上，协同调用可以利用的空闲资源对计算任务进行分发卸载，而为激励移动终端资源共享，以客户端(请求资源方)作为买方，以代理端(资源共享方)作为卖方，利用分布式买卖博弈机制，分别建立买卖双方的最优化模型，并提出基于斯坦伯格均衡的报价策略，作为一种有偿的任务卸载机制。

与现有技术相比本发明不仅可以有效地协调任务卸载与功率分配之间的关系，提高任务卸载效率以及系统资源利用率，还可以改善系统时延与能耗之间的均衡问题；采用买卖博弈的有偿任务卸载激励机制可以有效地激励代理端进行资源共享。

附图说明

图1为本发明任务卸载与功率分配联合决策方法流程示意图；

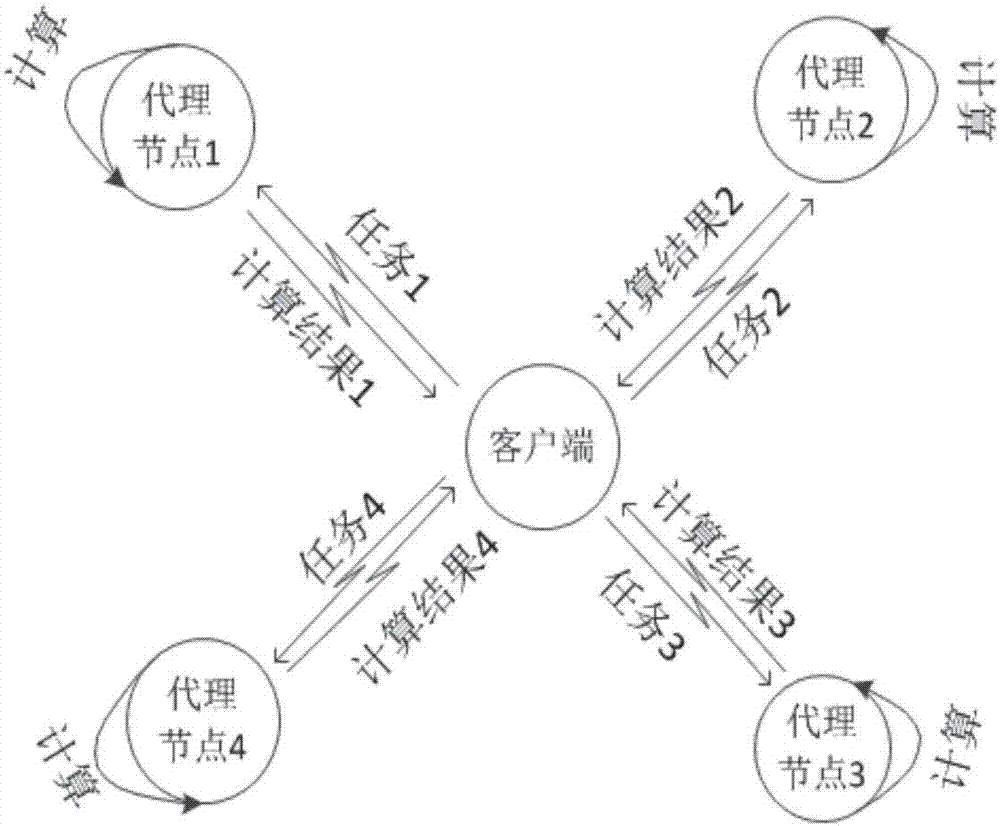
图2为本发明的资源卸载系统模型示意图；

图3为本发明任务卸载过程示意图；

图4为斯坦克伯格问题的两层主从决策结构示意图；

图5为本发明与现有技术系统收益仿真对比结果图；

图6为本发明与现有技术通信成本对比结果图；

图7为本发明与现有技术系统能耗对比结果图；

图8为本发明与现有技术系统延迟仿真对比结果图。

具体实施方案

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图对本发明实施例进一步详细说明。

本发明对移动终端进行划分，将在adhoc云网络中具有计算密集型任务的终端作为客户端，具有空闲资源的终端作为代理节点。

如图2所示，在adhoc移动云环境中，云网络中具有计算任务卸载请求移动终端为客户端，具有空闲资源的共享移动终端称为代理节点，客户端ci将自身的部分计算任务通过无线网络(如wifi、3g、4g等)卸载给代理节点aj，代理节点计算，然后将计算结果返回给客户端。相对于传统方法，使用任务卸载方法提高了客户端的任务处理效率，节省自身能耗。

图3为任务卸载过程所花时间。包括任务提交过程的时间t1，代理节点执行过程的时间t2、计算结果返回的时间t3。

假定任务传输中信道为加性高斯白噪声信道，且不考虑各终端移动性。用lij表示ci到aj的无线链路，用rij、pij表示链路lij上的数据流速率及消耗的功率。则：

其中，bij表示链路lij上的通信带宽，是信道增益，dij是ci到aj的传输距离，k为衰落因子，nij表示链路lij上的平均噪声功率。同理，用lji表示aj到ci的无线链路，rji，pji表示链路lji上数据流速率及消耗的功率，nji表示链路lji上的平均噪声功率。则有

bji表示链路lji上的通信带宽，gji是信道增益。假设客户端ci将任务分配到代理aj上可以获得任务卸载收益uij(wj)如下：

其中，θ是一个大于零的参量，是代理aj的处理能力。

为便于分析，假定代理终端aj需要等到ci将任务wj提交完成后才进行计算处理，并设定代理返回结果的大小为接收到数据大小的ρ倍(0＜ρ≤1)，则：

dij(wj)＝wj

dji(wj)＝ρdij(wj)

其中，dij(wj)为任务提交量，dji(wj)为计算结果返回量。

本发明定义客户端为买方、代理节点为卖方，利用买卖模型，分析买卖双方的行为并定义效用函数。

图4为本发明中买卖决策结构图。本发明的买卖博弈主要包括买方效用函数，卖方效用函数，双方策略。

为了充分利用代理节点帮助客户端卸载任务，需要确定客户端到每个代理节点的最优的任务卸载量wj。因此，本发明定义每一个客户端作为一个买方，每个代理节点为卖方。买方将支付给每个卖方一定的报酬激励卖方有偿任务卸载wj。另一方面，卖方进行有偿任务卸载的价格为每单位任务支付价格vj，卖方以此获取收益。

买方效用函数。买方效益来源为，受到代理节点帮助卸载而带来的收益减去为向代理支付的任务卸载费用、任务提交过程的数据传输开销、系统传输时延惩罚及买方能耗开销。

买方效用函数可以定义为：

其中，uj(wj)为受到代理节点帮助卸载而带来的收益，为买方bi向卖方支付的费用，vj表示卖方帮助买方任务卸载的单位价格，记为报价；qij(wj,pij)为任务提交过程的数据传输开销，为系统传输时延惩罚，为买方能耗开销。

由买方效用函数定义可知，买方旨在获取最大收益，因此买方效用函数最优化问题定义如下：

maxmize:

卖方效用函数。卖方效益来源为，买方向卖方支付的费用减去代理节点aj计算成本、代理节点结果返回的数据开销、卖方能耗开销。

卖方效用函数可以定义为:

其中，为卖方能耗开销，为代理节点aj的计算成本，qji(wj,pji)为代理节点将结果返回的数据传输开销。

由卖方效用函数定义可知，卖方旨在获取最大收益，因此卖方效用函数最优化问题定义如下：

maxmize:

本发明以买卖双方最大化各自的收益效用为依据，分析得到买卖双方各自的最优解

买卖双方最优解分析：

(1)买方最优解。移动adhoc云计算环境中，买方会根据卖方的属性及信道状态等信息为不同的卖方划分不同的计算任务，由于买方旨在最大化自身收益，综合提高卸载数据的处理效率，因此可以通过观察买方的效用函数与向卖方支付的费用关系判断:

其中αij为客户端单位时间传输开销因子。为客户端的时延惩罚因子。由计算可知即是分别关于wj，pij的凸函数。

因此买方最优化问题可以利用拉格朗日乘子法求解约束优化问题：

其中λ1，λ2为拉格朗日乘子。利用卡罗需-库恩-塔克条件kkt(karush-kuhn-tucker)可得：

当且时，可以得到一个买方最优任务卸载量w^*j及最优功率资源分配决策值p^*ij：

wj^*＝f1(pij^*,vj,λ1^*)

pij^*＝f2(wj^*,vj,λ2^*)

其中f1是wj的函数，f2是pij的函数，λ1^*和λ2^*是当得到w^*j和p^*ij的拉格朗日乘子。

(2)卖方最优解。将带入卖方效用函数最优问题定义式。值得注意的是，上式对于卖方而言为一个是一个典型的非合作博弈，需要考虑卖价vj和收益之间的权衡。如果卖方sj的卖价vj较低，买方更愿意购买更大的资源。显然，随着vj的增加，卖方的收益不断提高，但同时买方的代价也会增加，从而降低买方的收益，使得购买卖方资源wj的意愿降低，最终影响到卖方的收益。因此，vj一定存在一个特定值，使得买方不能继续通过增加wj的购买来提高其收益，此时如果继续增加vj，买方会减小wj的购买量，从而降低卖方的收益。因此，卖方存在最优卖价。

同理：

其中，ηj为代理节点aj单位时间计算能耗销开销。由计算可知且即是关于vj，pji的凸函数。因此卖方最优化问题可以利用拉格朗日乘子法求解约束优化问题：

其中，φj为拉格朗日乘子。当且可以得到卖方的最优价格决策值vj^*，以及最优分配功率资源pji^*。

vj^*＝g1(wj^*,pji^*,φj^*)

pji^*＝g2(wj^*,vj^*,φj^*)

其中g1是vj的函数，g2是pji的函数，φj^*是当得到vj^*和pji^*的拉格朗日乘子。

因此，买方先得到一个最优任务卸载量wj^*和最优功率资源分配pij^*。卖方在这一前提下得到最优卖价vj^*和最优功率资源分配pji^*。

斯塔克伯格博弈均衡解的存在性：

在本实施例中，证明了买卖双方的最优解wj^*和vj^*即为斯塔克伯格博弈均衡解，并通过下面的性质及证明说明了均衡解的最优。首先定义博弈的斯塔克伯格均衡解如下:

定义：wj^se和vj^se是斯塔克伯格均衡解，如果对于任意的j∈[1,n]，当代理终端的单位价格(报价)vj固定时，有：

同时，当客户端所分配的计算卸载wj固定时，有：

通过下面通过三个引理，证明

引理1.当vi固定不变时，在wj^*这一点上取得最大值，其中0≤wj^*≤wtotal。

证明：

则是关于wj的凸函数，且0≤wj^*≤wtotal，因此wj^*满足定义，是斯塔克伯格均衡解wj^se。

引理2.对于代理节点aj，随vj的增加而减少。

证明：对wj^*关于vj的一阶导可得：

其中上式说明wj^*是关于vj的减函数。这也符合实际物理场景，即当价格vj升高时，客户端会减少对该代理的计算任务wj购买。

引理3.最优确定时，lsj(vj,pji,φj)就是关于vj的凸函数。

证明：

显然所以，是关于vj的凸函数，且vj^*是se均衡解vj^se。

综上可得，最优解(wj^*,vj^*)为最优任务卸载决策，同时也是斯塔克伯格均衡解(wj^se,vj^se)。

本发明客户端根据当前的网络环境选择为代理节点卸载多少计算任务，从而确定客户端自身功率分配策略

代理节点为获得最高的目标收益，每个卖家基于系统环境和计算卸载任务成本逐渐增加其卖价vj，直到收益不能再改善为止，此时卖价在约束条件下达到最优，代理收益达到最大。此过程中，逐渐从正数变为0，也同时表明了卖家不能再通过提高卖价来提高自身收益。

因此设计一价格更新函数，允许每个卖家不断修改卖价，逐步达到收益最优。而在每次迭代过程中，卖家收益随卖价vj更新，直到最终收敛到最优报价vj^*。为了获得最优报价，价格迭代从开始，即：

又由于因此得到：

上式进一步描述：v≤i(v)。其中v＝(v11,...,vmm)，vij为代理节点aj向请求客户端ci处理计算任务的报价，则所构建的价格更新函数为i(v)＝(i11(v),...,imm(v))。进一步得到卖家报价的更新过程如下：

v(t+1)≤i(v(t))

假设客户端卸载任务量wj从0开始，代理节点报价vj从成本开始，根据wj^*＝f1(pij^*,vj,λ1^*)计算此时的wj和pij，并带入vj^*＝g1(wj^*,pji^*,φj^*)，更新代理节点的报价及功率，直到卖家报价收敛至最优，并以此得到最优的发送功率。代理节点将价格反馈给客户端，则客户端的最优任务策略确定。

图5－图8分别为现有的集中式waspa算法、本发明的分布式waspa算法、现有的贪婪式算法下的系统收益、通信成本、能耗以及系统延迟。

从图5中可以看到，当卸载任务量较小时，随着任务量的增加系统收益快速增加，这是由于任务卸载量越多，系统收益越高；而随着任务卸载量变大(如大于100mbit时)，系统收益增加逐渐减慢，甚至开始减小，这是由于任务卸载不断增大，任务卸载时延与系统能耗也变得越来越大，并成为影响系统收益的主要原因；另外，从图中可以看到，集中式waspa算法的收益最高，分布式waspa算法的收益次之，这是由于集中式waspa算法是基于系统全局信息，以系统全局收益最大为目标，可以得到使得系统收益最优的任务卸载及功率分配策略，但是算法时间复杂度较高，而分布式waspa算法是基于个体收益最大化制定任务卸载策略，显然个体的收益最大化不一定能够使得系统全局收益达到最大化，但分布式waspa算法的时间复杂度较低；此外，基于贪婪式ga算法的收益最低，这是由于ga算法在制定自身任务卸载策略时，并没有充分考虑终端功率对系统时延和卸载能耗的影响。

在图6－8中，可以看到虽然集中式waspa算法的通信成本最低，同时有较低的传输延，但与分布式waspa算法相比也造成了系统能耗较高。而从图8中可以看到，ga算法虽然以充足的传输功率获得较低的任务传输延迟，但这也造成了系统能耗和任务传输成本的增加。

以上所举实施例，对本发明的目的、技术方案和优点进行了进一步的详细说明，所应理解的是，以上所举实施例仅为本发明的优选实施方式而已，并不用以限制本发明，凡在本发明的精神和原则之内对本发明所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。