频分全双工低速高精度边带抑制方法与流程

本发明属于无线通信与微波技术领域，针对宽带频分全双工收发器的边带泄露问题提出低速高精度边带抑制解决方法,具体是频分全双工低速高精度边带抑制方法。此技术可应用于未来5g无线通信系统。

背景技术

得益于双工机的使用，频分全双工收发器的发射通道和接收通道可实现天线共享。由于发射信道中功率放大器的非线性作用，发射端频谱会出现带外频谱衍生问题，内嵌于频分收发器中的滤波器可以在一定程度上对接收频段和发射频段进行隔离。但当边带泄露能量过高时，剩余的带外频谱会泄露到接收端，降低接收机的灵敏度。

针对发射端带外频谱泄露问题，目前依据解决方案的实施位置，分为发射端和接收端抑制策略。发射端抑制方案在发射信道中插入预失真矫正模块对功率放大器的带外非线性进行矫正，消除严重的带外频谱泄露现象，频分双工机中的滤波器将进一步抑制带外干扰信号，从而提高接收端的敏感度。接收端抑制方案则允许带外频谱泄露的存在(即放宽对发射端线性度的要求)，通过多种不同的方法产生相同或近似的带外干扰信息，最后将干扰信息在接收端减掉，从而还原出原始接收信息。

由于接收端抑制策略是本专利的主要研究方向，现就切实有效的数字边带抑制方案做进一步介绍。数字边带抑制策略主要采用功率放大器行为模型对其非线性特性进行建模。具体操作为：1.功率放大器的原始信息经过功率放大器行为模型(也作边带抑制模型)还原出功率放大器的全带输出频谱；2.数字滤波器将对应的泄露干扰信号截取出来，将干扰信号从接收信息中减掉。至此，带外频谱衍生对接收机敏感度下降的影响将会消除。

然而，在5g无线通信系统中，发射信号的带宽在不断的增大，由于功率放大器的非线性作用，输出信号带宽将延拓为输入信号带宽的5倍。为了能完整的还原出功率放大器的输出频谱，数字端抑制算法的工作速率也将以5倍的速度增加。这就无形中增加了整个系统中adc，dac，以及数字模块的运算速率(即工作带宽)。若在操作过程中，降低工作带宽，则会导致频谱混叠现象，频谱混叠将会降低拟合的泄露频谱精度，进而破坏边带抑制效果。为解决5g中超大工作带宽问题，文章《digitalsuppressionoftransmitterleakageinfddrftransceivers:aliasingeliminationandmodelselection》提出了低速数字边带抑制算法。此算法提供了频谱混叠消除方案，使低速边带抑制方案首次在理论上成为可能。

频谱混叠现象出现的原因归咎于所需采样点的丢失，上述文章提出了遗失采样点补偿技术，此项技术摈弃了传统繁琐的上采样技术，在低速运行的情况下利用模型交叉项拟合遗失的数据点，并加以理论证明。同时，文章也提及，模型仅能近似遗失数据点，并不能做到精确还原数据信息。经过本专利申请人的长期研究，发现上述模型精度低的原因是由于没有合理考虑信号相位的非线性特性补偿。因此，本专利针对现有技术中存在的不足，在频谱混叠消除方案的基础上进行技术改进，提出新颖低速高精度数字边带抑制方法。此外，相对于现存技术，所述技术需要的模型系数更少。

技术实现要素：

本发明的目的是针对现有技术存在的不足，提出新颖低速高精度数字边带抑制方法。本发明抑制方法具体包括以下四个步骤：输入信号频谱搬移，边带抑制模型构建，边带频谱截取以及干扰信息消除。

步骤(1)、输入信号频谱搬移。

由于频分全双工收发器的发射频点和接收频点在射频域上存在差值，但矫正模型工作在信号基带，也就是基带的发射信号和接收信号中心频点为0。将所述差值进行补偿，可以确保边带抑制模型生成的边带干扰信息落在接收频段，即干扰信号的中心频点与接收频点相同(都为dc)，有利于后续的边带消除工作。频移过程可以通过频谱搬移算法实现，如公式(1)：

其中，和为功率放大器的输入信号和频谱搬移之后的信号。δω为接收频点和发射频点的频率差值。n为采样点个数。fs是采样频率。j为虚数符号。

步骤(2)、边带抑制模型的构建

将步骤(1)频谱搬移之后的信号作为边带抑制模型的输入，用于生成功率放大器输出频谱。传统的抑制模型为dvr模型(依据上述背景技术提及的文章)：

其中，是模型输出信号，βk是在输入信号范围内等距划分的k个域值结点。m是模型记忆长度。为模型系数。θ是采样点的相位。此模型通过绝对值运算产生无限延拓的频谱，具有较强的非线性拟合能力。本专利基于传统的dvr模型，对其进行技术改进，提出了高精度的新颖模型，下面将从原理上进行推导解说。

dvr边带抑制模型可以实现频谱混叠消除功能，原理可以通过一个简单的实例进行解说。假设采样数据序列由于欠采样的原因，丢失了偶数位的数据点理论上一个遗失的采样点，可以通过相邻的两个数据点的平均值进行近似。因此，数据点可以通过公式(3)进行近似还原：

功率放大器的非线性主要通过记忆多项式进行表述，则遗失数据点的三阶无记忆多项式表述为：

其中，θ1,θ3分别是采样点的相位。公式(4)表明三阶无记忆高阶项中包含交叉项和为了将遗失数据点的高阶非线性特征表述在dvr模型中，dvr模型结合自身模型的特点采用交叉项对遗失高阶非线性近似拟合，如此可以有效地消除由低速运行速率导致的信息遗失问题，即频谱混叠现象。

上述dvr模型主要是补偿跟模值相关的非线性特性，而相位信息由采样点自带的相位信息直接提供。如果对公式(4)进行深入研究，可以发现多项式的表述不仅仅跟模值相关的非线性特性有关，(虽然模值相关的非线性因素占主导作用)，但是相位相关的非线性特性在数据还原过程中也起着重要的作用，即在公式(4)中的相位差信息cos(θn-θn+i)＝cos(δθn)。相位差信息可以通过模型(2)进行部分补偿，但是要得到精确的还原效果却十分困难。主要原因是相位差变化的动态范围会随着采样率的下降而增大。在采样率足够高时，采样点之间的相位基本相同，也就是说相位差趋于零。观察发现89％的相位差的cos值落在(0.98,1]的狭窄区间内，也就是与相位差有关的非线性特性不占主导地位，大部分可以通过定值来还原。当采样率下降6倍频后，落在区间(0.98,1]仅占29％,(0.85,0.98]占36％，(0.5,0.85]占19％，(0,0.5]占16％,可见相位差的动态范围急剧扩散。因为，在低速条件下，相位差在构建模型过程中是一个不可忽视的重要变量。

从前面的公式推导可以看出，相位差cos(θn-θn+i)＝cos(δθn)由(4)得来，而(4)是由(3)推导而来。如果交叉项表征模值相关的非线性特性，那么求和项与交叉项的嵌套可以表征相位相关的非线性特性。前面的例子是通过均值方法代替求和项，但均值表达式是最简单的一种情况，为了增加模型的灵活度和拟合能力并尽量降低模型的复杂度，此处提出新求和项表达式为引入的λ可以依据具体的信号特性对相邻采样点进行权重分配。

根据dvr模型中的非线性表达特征，通过表征模值相关的非线性特征，将求和项与交叉项进行嵌套，最后得到了本专利所述新模型：

所述模型(5)与dvr模型相比较，除了增加了变量λ，还增加了非线性项的复杂度以提高模型拟合的准确性，比如将第三求和项中最后相乘的替换成本专利所述模型采用了更少的模型系数，但却有效地提高低速数字边带抑制模型的精度。

步骤(3)、边带频谱截取。

由于边带抑制模型产生的输出信号在频谱上无限延拓，为了限制边带信息的信号带宽，采用数字滤波器滤除带外多余信息，此操作可以通过如下公式(6)实现

其中，为滤波后的边带信号，是滤波之后的模型系数，h滤波器的脉冲响应，*表示为滤波器的卷积运算符。

步骤(4)、边带干扰信号消除。

最后，接收信号减去边带干扰信号，恢复原始信号的保真度。

其中，和分别是接收信号和消除干扰信息后的原始信号。

对于所述模型的参数提取问题，本专利提出如下解决方案。由于所述模型系数与模型为非线性相关，参数提取分为两步：首先，设置λ为定值，此时剩余模型系数与模型关系转变为线性关系，剩余的模型系数可以通过最小二乘法进行提取；接下来，在一定范围内对λ进行数值遍历，对应每一个λ模型的剩余系数通过最小二乘法获得，通过边带抑制效果对比，寻找模型的局部最优解。

所述模型的优势：所述模型(5)在dvr模型基础上进行技术改进，不仅可以实现频谱混叠消除功能，而且可以提高边带抑制精度。后续的实施例子中将对两个模型进行结果对比，从而对本专利的可行性和高精度性提供依据。

附图说明

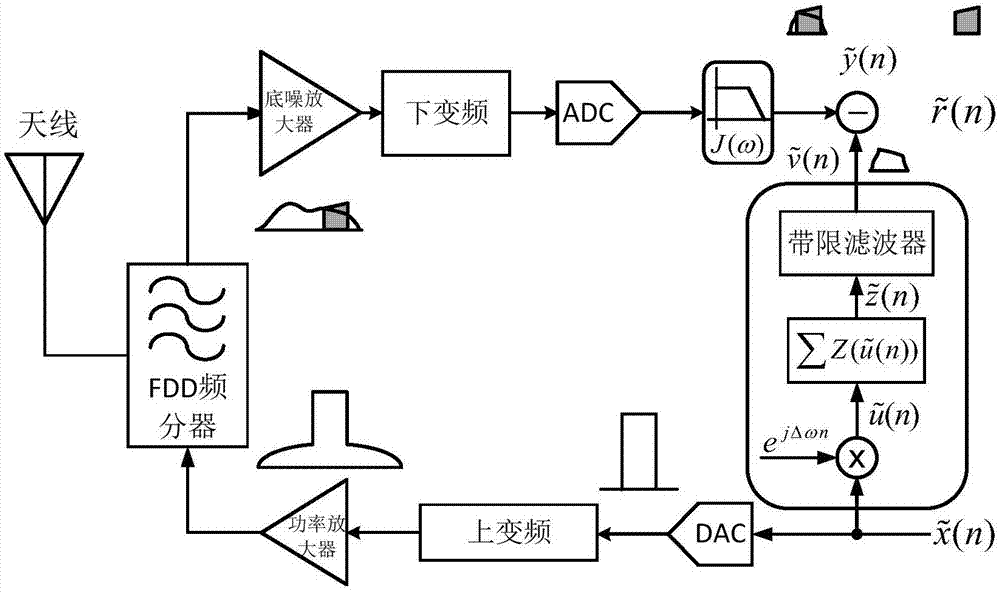
图1是本发明的频分全双工边带抑制方法的系统图；

图2是本发明的测试系统架构图；

图3是相位差值分布图；

图4是全带边带抑制效果图；

图5是降采样频谱混叠效果图；

图6是系数λ相对于nmse的数值关系图；

图7是现存技术和所述技术的边带抑制效果对比图。

具体实施方式

下面结合具体实施例对本发明做进一步分析。

如前所述，图1解释了带外频谱衍生对接收端信号的干扰机理，并结合本专利提出的具体数字边带抑制算法，对方案的步骤进行了分步解说。为了更好的解释此模型的应用过程和应用效果，搭建如图2所示的系统构架图。系统包含电脑，fpga基带模块，函数信号发生器，频谱分析仪以及核心元器件功率放大器。20mhz的基带信号作为激励源，经过上变频模块，上变频到2.14ghz射频信号，通过功率放大器传送至天线。在此实例系统中，由于测试系统的硬件限制，没有接入接收机，而是利用反馈电路将功率放大器的全带输出信号下变频到基带，通过adc采集回来，边带干扰信息通过滤波器截取出来，作为模型的目标函数，即模型的输出参考信号。因此，系统的接收信道响应被视为理想状态。此处的目的是在实验环境相同的情况下，对现有的技术和所述技术进行实验对比，虽然接收信道的响应为理想状态，但仍然可以公平地对比两个模型的边带抑制性能。

本发明抑制方法具体包括以下四个步骤：输入信号频谱搬移，边带抑制模型构建，边带频谱截取以及干扰信息消除。

步骤(1)、输入信号频谱搬移。

由于频分全双工收发器的发射频点和接收频点在射频域上存在差值，但矫正模型工作在信号基带，也就是基带的发射信号和接收信号中心频点为0。将所述差值进行补偿，可以确保边带抑制模型生成的边带干扰信息落在接收频段，即干扰信号的中心频点与接收频点相同(都为dc)，有利于后续的边带消除工作。频移过程可以通过频谱搬移算法实现，如公式(1)：

其中，和为功率放大器的输入信号和频谱搬移之后的信号。δω为接收频点和发射频点的频率差值。n为采样点个数。fs是采样频率。j为虚数符号。

步骤(2)、边带抑制模型的构建

将步骤(1)频谱搬移之后的信号作为边带抑制模型的输入，用于生成功率放大器输出频谱。传统的抑制模型为dvr模型(依据上述文章)：

其中，是模型输出信号，βk是在输入信号范围内等距划分的k个域值结点。m是模型记忆长度。为模型系数。θ是采样点的相位。此模型通过绝对值运算产生无限延拓的频谱，具有较强的非线性拟合能力。本专利基于传统的dvr模型，对其进行技术改进，提出了高精度的新颖模型，下面将从原理上进行推导解说。

dvr边带抑制模型可以实现频谱混叠消除功能，原理可以通过一个简单的实例进行解说。假设采样数据序列由于欠采样的原因，丢失了偶数位的数据点理论上一个遗失的采样点，可以通过相邻的两个数据点的平均值进行近似。因此，数据点可以通过公式(3)进行近似还原：

功率放大器的非线性主要通过记忆多项式进行表述，则遗失数据点的三阶无记忆多项式表述为：

其中，θ1,θ3分别是采样点的相位。公式(4)表明三阶无记忆高阶项中包含交叉项和为了将遗失数据点的高阶非线性特征表述在dvr模型中，dvr模型结合自身模型的特点采用交叉项对遗失高阶非线性近似拟合，如此可以有效地消除由低速运行速率导致的信息遗失问题，即频谱混叠现象。

上述dvr模型主要是补偿跟模值相关的非线性特性，而相位信息由采样点自带的相位信息直接提供。如果对公式(4)进行深入研究，可以发现多项式的表述不仅仅跟模值相关的非线性特性有关，(虽然模值相关的非线性因素占主导作用)，但是相位相关的非线性特性在数据还原过程中也起着重要的作用，即在公式(4)中的相位差信息cos(θn-θn+i)＝cos(δθn)。相位差信息可以通过模型(2)进行部分补偿，但是要得到精确的还原效果却十分困难。主要原因是相位差的变化的动态范围会随着采样率的下降而增大。此问题可以结合图3进行说明，在采样率足够高时，采样点之间的相位基本相同，也就是说相位差趋于零。图3(a)发现89％的相位差的cos值落在(0.98,1]的狭窄区间内，也就是与相位差有关的非线性特性不占主导地位，大部分可以通过定值来还原。当采样率下降6倍频后，落在区间(0.98,1]仅占29％,(0.85,0.98]占36％，(0.5,0.85]占19％，(0,0.5]占16％,图3(b)可见相位差的动态范围急剧扩散。因为，在低速条件下，相位差在构建模型过程中是一个不可忽视的重要变量。

从前面的公式推导可以看出，相位差cos(θn-θn+i)＝cos(δθn)由(4)得来，而(4)是由(3)推导而来。如果交叉项表征模值相关的非线性特性，那么求和项与交叉项的嵌套可以表征相位相关的非线性特性。前面的例子是通过均值方法代替求和项，但均值的表达式是最简单的一种情况，为了增加模型的灵活度和拟合能力并尽量降低模型的复杂度，此处提出新的求和项表达式为引入的λ可以依据具体的信号特性对相邻采样点进行权重分配。

根据dvr模型中的非线性表达特征，通过表征模值相关的非线性特征，将求和项与交叉项进行嵌套，最后得到了本专利所述新模型：

所述模型(5)与dvr模型相比较，除了增加了变量λ，还增加了非线性项的复杂度以提高模型拟合的准确性，比如将第三求和项中的最后相乘的替换成本专利所述模型可以有效提高低速数字边带抑制模型的精度。

步骤(3)、边带频谱截取。

由于边带抑制模型产生的输出信号在频谱上无限延拓，为了限制边带信息的信号带宽，采用数字滤波器对带外多余信息滤除，此操作可以通过如下公式(6)实现

其中，为滤波后的边带信号，是滤波之后的模型系数，h滤波器的脉冲响应，*表示为滤波器的卷积运算符。

步骤(4)、边带干扰信号消除。

最后，接收信号减去边带干扰信号，恢复原始信号的保真度。

其中，和分别是接收信号和消除干扰信息后的原始信号。

全带的采样率为368.64mhz，假设发射频点和接收频点的差值为30.72mhz，此处给出全带的边带抑制效果图4作为参考基准。泄露频谱曲线为发射信道频谱泄露的能量曲线。抑制后噪声曲线是将拟合的干扰信号减掉之后的残余干扰噪声。可以观察到在全带采样率的情况下，残余干扰已经接近系统噪声。接下来，368.64mhz高频速率经降采样至61.44mhz，图5说明在低速速率下的频谱混叠现象。泄露频谱(无混叠)是全带的信道频谱泄露能量曲线，泄露频谱(有混叠)是降采样之后的信道频谱泄露能量曲线，混叠频谱是前两个频谱相减得到的混叠频谱曲线。可以观察到混叠频谱能量和全带频谱泄露能量基本相同，暗示频谱混叠对接收信息造成较强干扰。

在频谱混叠存在的情况之下，现有技术和所述技术通过低速边带抑制矫正模型生成带外干扰信息。现有技术的模型参数设置为：m＝3，k＝10，共需要83个系数。所述技术参数设置为：m＝4，k＝5，共需要59个模型系数。dvr模型的参数提取采用最小二乘法。所述模型的参数提取采用发明内容中所述方案，对λ进行遍历，后利用最小二乘法求解模型系数，通过效果对比获得局部最优解。可依据归一化均值方差(nmse)的数值获得最优解。nmse用以表征模拟干扰信号和真实泄露信号的相似度，数值越小，相似度越高。图6表述了系数λ相对于nmse的数值关系。实验结果表明λ＝1.75为边带抑制效果的局域最佳值，同时λ＝1跟最佳值的边带抑制效果相仿。因此，在一般的情况下，可以将λ设为固定值1，从而降低模型参数提取的复杂度。图7表述现存技术和所述技术消除边带干扰后的效果图，泄露频谱曲线为真实信道频谱泄露的能量曲线，dvr模型指基于dvr模型边带抑制的残余噪声，所述模型(λ＝1.75)指所述模型当λ＝1.75时的边带抑制残余噪声，所述模型(λ＝1)指所述模型当λ＝1时的边带抑制残余噪声。可以看出所述技术的底噪数值更低，表明边带干扰消除之后原始信息的保真度更高。并且λ＝1所述模型的边带抑制效果与λ＝1.75的边带抑制效果相近。相关的指标数值罗列在表一中，所述技术比现存技术不仅所需的模型系数少，并且在nmse和底噪方面分别提升了2～3db。

表一.现存技术和所述技术各项指标对比。

实例测量和结果分析表明所述专利方法可以提高低速数字边带抑制矫正的精度，并且所需模型系数更少。