一种基于格的高效紧凑加密方法与流程

1.本发明涉及密码技术，尤其涉及基于格的后量子加密方法。


背景技术：

2.ibm的工程师们预测在未来的二十年内，量子计算机必将被大规模应用。一旦量子计算机被大规模制造出来，大多数基于离散对数、椭圆曲线离散对数或者大整数分解的公钥密码系统都将会被攻破。因此无论我们是否能够准确预测量子计算时代的到来时间，我们都需要将目前的信息安全系统提升到抗量子级别。
3.格密码是目前对抗量子攻击的主要数学方法之一。在密码学中，和其他古典的格困难问题(例如svp和cvp)相比，lwe(learning with error) 问题已经被证明有更加全面的功能。
4.对于正连续数σ＞0与x∈r，定义高斯函数令表示上的一维离散高斯分布，由概率密度函数决定。令表示在上的n维球面离散高斯分布，其中每个坐标都独立于给定正整数n和q，它们都是安全参数λ中的多项式中的参数，并给定整数向量和一个定义在上的概率分布χ，随机均匀选择噪音e
←
χ，令a
q,x,χ
是上的分布，并输出噪音分布χ通常被认为是离散高斯概率分布但是也可以采用其他的分布。
5.在判定型lwe假设中，对足够大的安全参数λ，概率多项式时间算法无法以不可忽略的概率来区分a
q,s,χ
和上的均匀分布。即使敌手看到多项式多个样本，且秘密向量x是从χ
n
随机选取的，这也是成立的。
6.mlwe问题是lwe问题的变体。来自mlwe分布的样本形式为其中为环，为m阶分圆多项式，l和h为矩阵样本的维度，从环中随机选取计算得到y
i
＝a
i
x+e
i
，所有样本使用相同的和相同或不同的其中，i用于标记次数，与分别为两个分布，分布参数记为η1与η2，分布可相同也可不同。mlwe问题是从多项式个来自mlwe分布的样本中恢复x。具体地，对于敌手a，定义
[0007][0008]
如果没有最多运行t时间的算法a的优势大于ε，我们称(t,∈)-mlwe
h,l,η
困难性假设成立。
[0009]
基于mlwe的困难性，可构造公钥加密机制。一个公钥加密机制可由算法构成的三
元组pke＝(gen,enc,dec)来给出，对于任意的κ∈n，有
[0010]
1)gen：密钥生成算法，是一个概率多项式时间算法，输入1
κ
并输出一对字符串(pk,sk)，(pk,sk)分别被称为公钥和私钥，该过程可以写作(pk,sk)
←
gen(1
κ
)。
[0011]
2)enc：加密算法，是一个概率多项式时间算法，其从明文空间msp 取公钥消息m，并从随机数空间随机选取r，并产生密文c∈{0,1}
*
，该过程记为c
←
enc
pk
(m；r)。
[0012]
3)dec：解密算法，是一个确定性的多项式时间算法，输入密钥sk和密文c∈{0,1}
*
，并返回消息m∈msp。
[0013]
如果对任意的κ∈n，每对(pk,sk)都由gen(1
κ
)生成，且每个m∈msp，都有e[max
m∈msp
pr[dec
sk
(enc
pk
(m))≠m]]≤δ，则说该pke机制是δ正确的。
[0014]
一个密钥封装机制kem＝(cen,encaps,decaps)包括了三种算法。输入安全参数κ，密钥生成算法gen输出密钥对(pk,sk)，pk也定义了一个有限的密钥空间κ。而封装算法encaps在输入pk时输出二元组(k,c)，其中c是密钥k的一个封装，而k则包含在密钥空间κ中。确定的解封装算法decaps在输入sk和一个密钥封装c后，输出密钥k＝decaps(sk,c)∈κ，或符号
⊥
以表示c不是一个有效的密钥封装。
[0015]
如果pr[decaps(sk,c)≠k|(pk,sk)
←
gen(1
κ
)；(k,c)
←
encaps(pk)]≤δ，那么我们称kem是δ正确的。


技术实现要素：

[0016]
一种基于格的高效紧凑加密方法，其中，一个字符串或者值α都表示二进制的值，|α|表示α二进制的长度；对于任意实数x，表示小于等于x的最大整数，表示大于等于x的最小整数，对于任意的正整数a和b，用lcm(a,b)表示a和b的最小公倍数；对于任意的并且i＜j，用[i,j]表示整数集合{i,i+1,...,j-1,j}；对于任意的正整数t，令表示表示中的元素默认表示为[0,t-1]，但有时会明确表示为会明确表示为表示群中二进制长度为n的元素集合；
[0017]
如果s是一个有限集合，那么|s|表示它的基数，并且x
←
s表示均匀随机的从s中取一个元素；对于两个集合我们定义 a+b＝{a+b|a∈a,b∈b}；对于一个加法群(g,+)，元素x∈g并且子集 x+s表示将s中每一个元素都和x相加结果的集合；对于一个集合s，用 u(s)表示s的一个均匀分布；对于任意的r中的离散随机变量x， supp(x)＝{x∈r|pr[x＝x]＞0}；
[0018]
如果d表示一个概率分布，那么x
←
d表示根据d选择一个元素并赋值给x；如果α既不是一个算法也不是一个集合，那么x
←
α就表示简单的赋值操作；如果a是一个概率算法，那么a(x1,x2,...；r)表示将x1,x2,...作为输入， r为随机种子a的运算结果；我们用y
←
a(x1,x2,...；r)表示随机选取r并令y为 a(x1,x2,...；r)的实验；用pr[r1；...；r
n
:e]表示事件e在一连串有序的随机过程 r1,...,r
n
之后发生的概率；如果对于任意的c＞0，对于所有的λ＞λ
c
，都存在一个λ
c
使得f(λ)＜1/λ
c
，那么函数f(λ)是可忽略的；定义环其中，为m阶分圆多项式；r
q
中的元素为n维多项式，其形式为a0+a1x1+a2x2+...+
a
n-1
x
n-1
，其中n是一个正整数；正整数l和h为矩阵样本的维度，表示h
×
l维的矩阵，每个元素为环r
q
上的n维多项式；对于输入是向量的函数，其运算是对向量的每一维分别处理计算；
[0019]
mlwe分布中的样本形式为mlwe问题是从多项式个来自mlwe分布的样本中恢复秘密值x；具体地，从环中随机选取计算得到y
i
＝a
i
x+e
i
，所有样本使用相同的和相同或不同的其中，正整数i用于标记次数，与分别为两个概率分布，分布参数记为η1与η2，分布可相同也可不同；对于敌手a定义
[0020][0021]
如果没有最多运行τ时间且优势大于ε的算法a，我们称(τ,∈)-mlwe
h,l,η
困难性假设成立；其中，τ是关于n的多项式，ε是关于n的可忽略函数；
[0022]
一个非对称共识算法akc＝(params,con,rec)，其中参数定义如下：
[0023]
1)params＝(q,m,g,d,aux)表示系统参数，2≤m,g≤q,且都为正整数，aux表示由(q,m,g,d)确定的辅助信息，其值可能为空；除非特别说明，本发明方法中的m＝2或4；
[0024]
2)v
←
con(σ2,k2,params)，con()为一种多项式时间算法，在输入为 (σ2,k2,params)的条件下，算法输出信号其中，其中，其中n和n
′
以及n为正整数，其值相等或不等；
[0025]
3)k1＝rec(σ1,v,params)，rec()为一种确定性多项式算法，在输入为 (σ1,v,params)的情况下，rec()输出的结果为其中，
[0026]
本发明的第一方面，所述方法包括：
[0027]
生成加密所需的系统参数(λ,n,q,χ,akc,l,h,t1,t2)；其中，λ为安全参数， q≥2，χ为噪音分布，l和h为正整数并且为λ的多项式，表示维度大小，t1和t2为压缩函数中使用的参数，用于发送密文时减小带宽而进行的操作；
[0028]
公私钥生成：解密者采样得到随机种子seed
←
{0,1}
κ
，seed的长度是正整数κ，利用gen输入种子seed生成矩阵a，其中，是一个伪随机生成器，将长度为κ的随机字符串映射到的矩阵a；所述解密者采样及其中，与分别为两个分布，用于采样l
×
1维的向量，其中向量的每一维元素是r
q
上的多项式，所述分布相同或不同；和/或作为私钥的一部分；所述解密者计算公钥 y1＝compress1(ax1+e1)，并将y1与seed作为公钥的一部分发送给加密者；其中，compress1()为一种压缩函数，该压缩函数的输入输出为二者均为环r
q
上l
×
1维的向量，每一维为n维多项式但多项式每一维的系数削减t1比特，其中t1≥0是整数；
[0029]
加密方法：所述加密者从中选取k2作为待加密消息，并根据得到的随机种子seed，使用相同的伪随机数发生器gen生成矩阵a＝gen(seed)；所述加密者采样
以及其中，与分别为两个相同或不同的分布，用于采样l
×
1维的向量，分布用于采样n维多项式，η1，η2，η3相等或不等；所述加密者计算：
[0030]
1)y2＝compress2(a
t
x2+e2)；其中，compress2()为一种压缩函数，该压缩函数的输入输出为均为环r
q
上l
×
1维的向量，每一维均为n维多项式但多项式每一维的系数削减t2比特，其中t2≥0是整数；加密者使用的compress2()与解密者使用的 compress1()函数相同或不同；
[0031]
2)σ2＝decompress1(y1)
t
·
x2+e
σ
；其中，decompress1()为一种解压缩函数，加密者使用的decompress1()需与解密者使用的compress1()函数对应，该解压缩函数的输入为输出解压缩结果，二者均为环r
q
上的l
×
1维向量，与e
σ
∈r
q
相加得到σ2∈r
q
，为n维多项式；
[0032]
3)v
←
con(σ2,k2,params)；其中，con()为非对称密钥共识akc中定义的多项式算法，输入为(σ2,k2,params)，算法con()输出
[0033]
所述加密者将和作为密文的一部分发送给所述解密者；
[0034]
解密方法：所述解密者收到y2与v以后，执行以下步骤：
[0035]
1)其中，decompress2()为一种解压缩函数，与加密者使用的compress2()相对应，该解压缩函数的输入输出解压缩结果，二者均为环r
q
上的l
×
1维向量，相乘得到σ1∈r
q
，为n维多项式；
[0036]
2)k1＝rec(σ1,v,params)；其中，rec()为确定性多项式算法，在输入为(σ1,v,params)的情况下，rec()输出的结果为
[0037]
con()和rec()有如下计算方式：对于多项式的每一个系数和和k2中的每一维系数
[0038]
1)共识方式-1：或者其中是v中对应维度的值；和/或
[0039]
2)共识方式-2：其中是v中对应维度的值；和/或
[0040]
3)共识方式-3：其中是v中对应维度的值；和/或
[0041]
4)共识方式-4：其中是v中对应维度的值；和/或
[0042]
5)共识方式-5：其中
是v中对应维度的值；和/或
[0043]
6)共识方式-6：其中是v中对应维度的值；和/或
[0044]
7)共识方式-7：其中是v中对应维度的值；和/或
[0045]
compress1()和/或compress2()的计算方式为如下的compress()； decompress1()和/或decompress2()的计算方式为如下的decompress()；令t≥0为一个整数且t∈{t1，t2}，如果t＝0表示不用做压缩和解压缩；注意对于发明方法实际应用中compress1()和/或compress2()所采用的具体的t值可以相等对应于t1＝t2，也可以不等对应于t1≠t2；对于多项式的每一个系数，记为
[0046]
1)压缩和解压缩方式-1：decompress(y)＝2
t
y；
[0047]
2)压缩和解压缩方式-2：decompress(y)＝2
t
y+2
t-1
；
[0048]
3)压缩和解压缩方式-3：decompress(y)＝2
t
y-2
t-1
；
[0049]
上面三种方式，但是如果y＝2
t-1
时压缩函数额外输出一个标识符，解压缩函数输入除了y还有这个标识符，此时解压缩输出2
t
y+2
t-1
或2
t
y-2
t-1
[0050]
4)压缩和解压缩方式-4：y＝compress(x)＝|2
t
x/q|或x/q|或decompress(y)＝|qx/2
t
|或
[0051]
5)压缩和解压缩方式-5：
[0052]
令n＝256或n＝512，l∈{1,2,3,4}，m∈{2,4,8，16，32,64,128,256}，g＝2
δ
,δ≥1为正整数；令分别是中心二项分布或均匀分布或是定义在有限区间的离散高斯分布或定义在有限区间的一个离散分布或定义在有限区间的包含上述分布的组合分布；
[0053]
具体而言，参数选取如下：
[0054]
·
参数集-1：n＝256，l＝2，η1＝η2＝η3＝1，q≤3329；
[0055]
·
参数集-2：n＝256，l＝3，η1＝η2＝η3＝1，q≤3329；
[0056]
·
参数集-3：n＝256，l＝2，η1＝η2＝η3≤4，q≤3329或q≤7681；
[0057]
·
参数集-4：n＝256，l＝4，m＝4，η1＝η2＝η3≤4，q≤3329或q≤7681；
[0058]
·
参数集-5：η1≠η2，q≤3329或t1＝0或q≤7681且n＝512；
[0059]
·
参数集-6：η1≠η2，q≤7681，且使用上述1)-3)压缩或解压缩函数；
[0060]
·
参数集-7：η1＝η2＝2且q≤3329，或η1＝η2＝4且q≤7681，且使用上述1)-4) 压缩或解压缩函数；
[0061]
·
参数集-8：n＝256，l＝3，m＝2，t1＝0，t2＝2，η1＝η2＝η3＝2，q≤3329， g＝8或16，且使用上述1)-3)压缩或解压缩函数；或n＝256，l＝2， m＝2，t1＝0，t2＝2，η1＝η2＝η3＝2，q≤3329，g＝8或16或4，且使用上述1)-4)压缩或解压缩函数；
[0062]
·
参数集-9：n＝256，l＝3，m＝2，t1＝t2＝4，η1＝1，η2＝η3＝4，q≤7681， g＝8或
16，且使用上述1)-5)压缩或解压缩函数；
[0063]
·
参数集-10：m≥3，或者使用共识方式-3或4或5或6或7，或者使用上述共识方式-1的con或rec共识机制且使用上述压缩和解压缩方式-3或4或5，或者使用上述共识方式-2的con或rec共识机制且使用上述压缩和解压缩方式-1或2或3或4，n＝256或512， l≥2，m≥2，t1≥0，t2,≥0，η1>0，η2>0,η3>0，q≤7681，g≥2。
[0064]
本发明的第二方面，所述方法包括：与与分别为三个分布，所述分布相同或不同，令η∈{η1,η2,η3}，所述分布的每一个分布为如下分布之一：
[0065]
1)[-η,η]上的均匀分布；
[0066]
2)中心二项分布b
η
，定义b
η
为sample(a0,
…
,a
η
,b1,
…
,b
η
)
←
{0,1}
2η
并输出的结果；
[0067]
3)[-η,η]上的离散高斯分布；
[0068]
4)有限区间上的包含上述分布的组合分布，比如中心二项分布和均匀分布的和或差。
[0069]
本发明的第三方面，所述方法包括：
[0070]
·
参数集-11：n＝256，l＝2，η1＝η2＝η3＝1，q≤3329，t1＝t2＝3，g＝8；
[0071]
·
参数集-12：n＝256，l＝2，η1＝η2＝η3＝1，q≤3329，t1＝0，t2＝3或4，g＝4 或8或16或32；
[0072]
·
参数集-13：n＝256，l＝3，η1＝η2＝η3＝1，q≤3329，t1＝t2＝3，g＝32；
[0073]
·
参数集-14：n＝256，l＝3，η1＝η2＝η3＝1，q≤3329，t1＝0，t2＝3，g＝8；
[0074]
·
参数集-15：n＝512，l＝2，η1＝η2＝η3＝2，q≤3329，t1＝0，t2∈{0，1，2}， g∈{8,16，32，64}；
[0075]
·
参数集-16：n＝512，l＝2，η1＝η2＝η3＝1，q≤3329，t1＝0，t2＝2，g＝8；
[0076]
·
参数集-17：n＝512，l＝2，η1＝η2＝η3＝1，q≤3329，t1＝t2＝2，g＝8；
[0077]
·
参数集-18：n＝256，l＝4，m＝4，η1＝η2＝η3＝2或4，q≤7681；
[0078]
·
参数集-19：n＝256，l＝4，η1＝η2＝η3＝2，q≤7681，t1＝t2＝1，g∈{16，32}；
[0079]
·
参数集-20：n＝256，l＝4，η1＝η2＝η3＝2，q≤7681，t1＝0，t2∈{0，1，2}， g∈{8，16}；
[0080]
·
参数集-21：n＝256，l＝2，m＝2,，η1＝η2＝η3＝1，q≤3329，t1＝0，t2＝4，g∈{8，16}；或n＝256，l＝3，m＝2,，η1＝η2＝η3＝1，q≤3329，t1＝0，t2＝3， g∈{4，8}；或n＝512，l＝2，m＝2,，η1＝η2＝η3＝1，q≤3329，t1＝0，t2＝3， g∈{8，16，32}；或n＝256，l＝4，m＝4,，η1＝η2＝η3＝1，q≤3329， t1＝0，t2∈{0,1}，g∈{32，64,128}；
[0081]
·
参数集-22：n＝256，l＝2，m＝2,，η1＝η2＝η3＝1，q≤3329，t1＝t2＝3，g∈{4,8}；或n＝256，l＝3，m＝2,，η1＝η2＝η3＝1，q≤3329， t1∈{3,4}，t2∈{3，4}，g∈{8，16,32,64}；或n＝512，l＝2，m＝2,，η1＝η2＝η3＝1， q≤3329，t1＝t2＝2，g∈{4，8，16}；或n＝256，l＝4，m＝4,，η1＝η2＝η3＝1， q≤3329，t1∈{0,1},t2∈{0,1}，g∈{16.32}；
[0082]
·
参数集-23：n＝256，l＝2，m＝2,，η1＝η2＝η3＝2，q≤7681，t1＝t2＝4，g∈{4,8，16}；或n＝256，l＝2，m＝2,η1∈{1，4}，η2＝η3∈{4，1}，q≤7681， t1∈{3，4,5}，t2∈{4，5}，g∈{4，8，16}；
[0083]
·
参数集-24：n＝512，l＝2，m＝2,η1＝η2＝η3＝2,q≤7681， t1∈{2,3}，t2∈{2，3}，g∈{4，8，16，32,64}；或n＝512， l＝2，m＝2,η1∈{1，4}，η2＝η3∈{4，1},q≤7681，t1∈{0，1，2,3,4},t2∈{0，1，2,3,4}，g∈{2，4,8，16,32，64,128,256}；
[0084]
·
参数集-25：n＝256，l＝4，m＝4,，η1＝η2＝η3＝2，q≤7681， t1∈{0，1，2},t2∈{0，1，2}，g∈{4,8，16,32，64}；或n＝256， l＝4，m＝4,η1∈{1，4}，η2＝η3∈{4，1},q≤7681，t1∈{0，1，2,3,4},t2∈{0，1，2,3,4}， g∈{2，4,8，16,32，64,128,256}。
[0085]
本发明的第四方面，所述方法包括：当m≥3，或者使用共识方式-3 或4或5或6或7，或者使用上述共识方式-1的con或rec共识机制且使用上述压缩和解压缩方式-3或4或5，或者使用上述共识方式-2的con 或rec共识机制且使用上述压缩和解压缩方式-1或2或3或4，参数设置如下：
[0086]
·
参数集-26：n＝256，l＝2，η1＝2，η2＝η3＝12，，q≤7681，t1＝3，t2＝4，，g＝8；
[0087]
·
参数集-27：n＝256，l＝3，η1＝1，η2＝η3＝4，，q≤7681，t1＝4，t2＝4，g＝16；
[0088]
·
参数集-28：n＝512，l＝2，η1＝2，η2＝η3＝8,，q≤12289，t1＝2或3，t2＝3 或4，g＝16；
[0089]
·
参数集-29：n＝256，l＝2，η1＝η2＝η3＝2，q≤3329，t1＝0，t2＝2或3， g＝8；
[0090]
·
参数集-30：n＝256，l＝3，η1＝η2＝η3＝2，q≤3329，t1＝0，t2＝2或3， g＝16；
[0091]
·
参数集-31：n＝256，l＝4，η1＝η2＝η3＝2，q≤3329，t1＝0，t2＝1或2， g＝32；
[0092]
·
参数集-32：n＝256，l＝4，m＝4，η1＝η2＝η3＝2，q≤7681，t1＝0，t2＝2， g＝32或64或128；
[0093]
·
参数集-33：n＝256，l＝4，m＝4，η1＝η2＝η3＝1，q≤3329，t1＝0，t2＝1或 2，g＝32或64或128或256；
[0094]
·
参数集-34：n＝256，l＝4，m＝4，η1＝η2＝η3＝1，q≤3329，t1＝1，t2＝1， g＝1024或512或2048；
[0095]
·
参数集-35：n＝256，l＝4，m＝4，η1＝η2＝η3＝1，q≤3329， t1＝0，t2＝0，g＝8或16或32或64或128或256。
[0096]
如上所述的方法，在具体计算两个多项式的乘法时，需要对多项式进行快速数论变换(ntt变换)。所述参数中，部分参数无法进行完整的传统ntt变换，可采取新型的ntt变换进行处理。
附图说明
[0097]
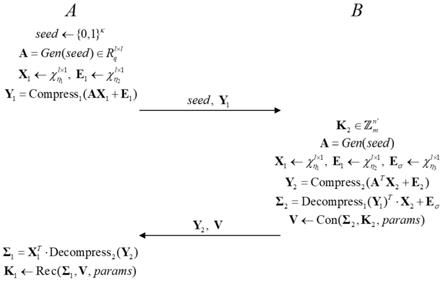
图1示例性地表示出了非对称共识算法的过程；
[0098]
图2示例性地表示出了本发明的基于格的加密方法。
具体实施方式
[0099]
生成加密所需的系统参数(λ,n,q,χ,akc,l,h,t1,t2)；其中，λ为安全参数， q≥2，χ为噪音分布，l和h为正整数并且为λ的多项式，表示维度大小，t1和t2为压缩函数中使用的参数，用于发送密文时减小带宽而进行的操作；
[0100]
公私钥生成(见图2)：解密者采样得到随机种子seed
←
{0,1}
κ
，seed的长度是正整数κ，利用gen输入种子seed生成矩阵a，其中，是一个伪随机生成器，将长
度为κ的随机字符串映射到的矩阵a；所述解密者采样及其中，与分别为两个分布，用于采样l
×
1维的向量，其中向量的每一维元素是r
q
上的多项式，所述分布相同或不同；和/或作为私钥的一部分；所述解密者计算公钥 y1＝compress1(ax1+e1)，并将y1与seed作为公钥的一部分发送给加密者；其中，compress1()为一种压缩函数，该压缩函数的输入输出为二者均为环r
q
上l
×
1维的向量，每一维为n维多项式但多项式每一维的系数削减t1比特，其中t1≥0是整数；
[0101]
加密方法(见图2)：所述加密者从中选取k2作为待加密消息，并根据得到的随机种子seed，使用相同的伪随机数发生器gen生成矩阵 a＝gen(seed)；所述加密者采样以及其中，与分别为两个相同或不同的分布，用于采样l
×
1维的向量，分布用于采样n维多项式，η1，η2，η3相等或不等；所述加密者计算：
[0102]
1)y2＝compress2(a
t
x2+e2)；其中，compress2()为一种压缩函数，该压缩函数的输入输出为均为环r
q
上l
×
1维的向量，每一维均为n维多项式但多项式每一维的系数削减t2比特，其中t2≥0是整数；加密者使用的compress2()与解密者使用的 compress1()函数相同或不同；
[0103]
2)σ2＝decompress1(y1)
t
·
x2+e
σ
；其中，decompress1()为一种解压缩函数，加密者使用的decompress1()需与解密者使用的compress1()函数对应，该解压缩函数的输入为输出解压缩结果，二者均为环r
q
上的l
×
1维向量，与e
σ
∈r
q
相加得到σ2∈r
q
，为n维多项式；
[0104]
3)v
←
con(σ2,k2,params)；其中，con()为非对称密钥共识akc中定义的多项式算法，输入为(σ2,k2,params)，算法con()输出
[0105]
所述加密者将和作为密文的一部分发送给所述解密者；
[0106]
解密方法(见图2)：所述解密者收到y2与v以后，执行以下步骤：
[0107]
1)其中，decompress2()为一种解压缩函数，与加密者使用的compress2()相对应，该解压缩函数的输入输出解压缩结果，二者均为环r
q
上的l
×
1维向量，相乘得到σ1∈r
q
，为n维多项式；
[0108]
2)k1＝rec(σ1,v,params)；其中，rec()为确定性多项式算法，在输入为(σ1,v,params)的情况下，rec()输出的结果为
[0109]
con()和rec()有如下计算方式(见图1)：对于多项式的每一个系数和和k2中的每一维系数
[0110]
1)共识方式-1：或者其中是v中对应维度的值；和/或
[0111]
2)共识方式-2：其中是v中对应维度的值；和/或
[0112]
3)共识方式-3：其中是v中对应维度的值；和/或
[0113]
4)共识方式-4：其中是v中对应维度的值；和/或
[0114]
5)共识方式-5：其中是v中对应维度的值；和/或
[0115]
6)共识方式-6：其中是v中对应维度的值；和/或
[0116]
7)共识方式-7：其中是v中对应维度的值；和/或
[0117]
compress1()和/或compress2()的计算方式为如下的compress()； decompress1()和/或decompress2()的计算方式为如下的decompress()；令t≥0为一个整数且t∈{t1,t2}，如果t＝0表示不用做压缩和解压缩；注意对于发明方法实际应用中compress1()和/或compress2()所采用的具体的t值可以相等对应于t1＝t2，也可以不等对应于t1≠t2；对于多项式的每一个系数，记为
[0118]
1)压缩和解压缩方式-1：decompress(y)＝2
t
y；
[0119]
2)压缩和解压缩方式-2：decompress(y)＝2
t
y+2
t-1
；
[0120]
3)压缩和解压缩方式-3：decompress(y)＝2
t
y-2
t-1
；
[0121]
上面三种方式，但是如果y＝2
t-1
时压缩函数额外输出一个标识符，解压缩函数输入除了y还有这个标识符，此时解压缩输出2
t
y+2
t-1
或2
t
y-2
t-1
[0122]
4)缩和解压缩方式-4：y＝compress(x)＝|2
t
x/q|或x/q|或decompress(y)＝|qx/2
t
|或
[0123]
5)压缩和解压缩方式-5：
[0124]
令n＝256或n＝512，l∈{1,2,3,4}，m∈{2,4,8，16，32,64,128,256}，g＝2
δ
,δ≥1为正整数；令分别是中心二项分布或均匀分布或是定义在有限区间的离散高斯分布或定义在有限区间的一个离散分布或定义在有限区间的包含上述分布的组合分布；
[0125]
具体而言，参数选取如下：
[0126]
·
参数集-1：n＝256，l＝2，η1＝η2＝η3＝1，q≤3329；
[0127]
·
参数集-2：n＝256，l＝3，η1＝η2＝η3＝1，q≤3329；
[0128]
·
参数集-3：n＝256，l＝2，η1＝η2＝η3≤4，q≤3329或q≤7681；
[0129]
·
参数集-4：n＝256，l＝4，m＝4，η1＝η2＝η3≤4，q≤3329或q≤7681；
[0130]
·
参数集-5：η1≠η2，q≤3329或t1＝0或q≤7681且n＝512；
[0131]
·
参数集-6：η1≠η2，q≤7681，且使用上述1)-3)压缩或解压缩函数；
[0132]
·
参数集-7：η1＝η2＝2且q≤3329，或η1＝η2＝4且q≤7681，且使用上述1)-4) 压缩或解压缩函数；
[0133]
·
参数集-8：n＝256，l＝3，m＝2，t1＝0，t2＝2，η1＝η2＝η3＝2，q≤3329， g＝8或16，且使用上述1)-3)压缩或解压缩函数；或n＝256，l＝2， m＝2，t1＝0，t2＝2，η1＝η2＝η3＝2，q≤3329，g＝8或16或4，且使用上述1)-4)压缩或解压缩函数；
[0134]
·
参数集-9：n＝256，l＝3，m＝2，t1＝t2＝4，η1＝1，η2＝η3＝4，q≤7681， g＝8或16，且使用上述1)-5)压缩或解压缩函数；
[0135]
·
参数集-10：m≥3，或者使用共识方式-3或4或5或6或7，或者使用上述共识方式-1的con或rec共识机制且使用上述压缩和解压缩方式-3或4或5，或者使用上述共识方式-2的con或rec共识机制且使用上述压缩和解压缩方式-1或2或3或4，n＝256或512， l≥2，m≥2，t1≥0，t2,≥0，η1>0，η2>0,η3>0，q≤7681，g≥2。
[0136]
本发明的第二方面，所述方法包括：与与分别为三个分布，所述分布相同或不同，令η∈{η1,η2,η3}，所述分布的每一个分布为如下分布之一：
[0137]
1)[-η,η]上的均匀分布；
[0138]
2)中心二项分布b
η
，定义b
η
为sample(a0,
…
,a
η
,b1,
…
,b
η
)
←
{0,1}
2η
并输出的结果；
[0139]
3)[-η,η]上的离散高斯分布；
[0140]
4)有限区间上的包含上述分布的组合分布，比如中心二项分布和均匀分布的和或差。
[0141]
本发明的第三方面，所述方法包括：
[0142]
·
参数集-11：n＝256，l＝2，η1＝η2＝η3＝1，q≤3329，t1＝t2＝3，g＝8；
[0143]
·
参数集-12：n＝256，l＝2，η1＝η2＝η3＝1，q≤3329，t1＝0，t2＝3或4，g＝4 或8或16或32；
[0144]
·
参数集-13：n＝256，l＝3，η1＝η2＝η3＝1，q≤3329，t1＝t2＝3，g＝32；
[0145]
·
参数集-14：n＝256，l＝3，η1＝η2＝η3＝1，q≤3329，t1＝0，t2＝3，g＝8；
[0146]
·
参数集-15：n＝512，l＝2，η1＝η2＝η3＝2，q≤3329，t1＝0，t2∈{0，1，2}， g∈{8,16，32，64}；
[0147]
·
参数集-16：n＝512，l＝2，η1＝η2＝η3＝1，q≤3329，t1＝0，t2＝2，g＝8；
[0148]
·
参数集-17：n＝512，l＝2，η1＝η2＝η3＝1，q≤3329，t1＝t2＝2，g＝8；
[0149]
·
参数集-18：n＝256，l＝4，m＝4，η1＝η2＝η3＝2或4，q≤7681；
[0150]
·
参数集-19：n＝256，l＝4，η1＝η2＝η3＝2，q≤7681，t1＝t2＝1，g∈{16，32}；
[0151]
·
参数集-20：n＝256，l＝4，η1＝η2＝η3＝2，q≤7681，t1＝0，t2∈{0，1，2}， g∈{8，16}；
[0152]
·
参数集-21：n＝256，l＝2，m＝2,，η1＝η2＝η3＝1，q≤3329，t1＝0，t2＝4， g∈{8，
16}；或n＝256，l＝3，m＝2,，η1＝η2＝η3＝1，q≤3329，t1＝0，t2＝3， g∈{4，8}；或n＝512，l＝2，m＝2,，η1＝η2＝η3＝1，q≤3329，t1＝0，t2＝3， g∈{8，16，32}；或n＝256，l＝4，m＝4,，η1＝η2＝η3＝1，q≤3329， t1＝0，t2∈{0,1}，g∈{32，64,128}；
[0153]
·
参数集-22：n＝256，l＝2，m＝2,，η1＝η2＝η3＝1，q≤3329，t1＝t2＝3， g∈{4,8}；或n＝256，l＝3，m＝2,，η1＝η2＝η3＝1，q≤3329， t1∈{3,4}，t2∈{3，4}，g∈{8，16,32,64}；或n＝512，l＝2，m＝2,，η1＝η2＝η3＝1， q≤3329，t1＝t2＝2，g∈{4，8，16}；或n＝256，l＝4，m＝4,，η1＝η2＝η3＝1， q≤3329，t1∈{0,1},t2∈{0,1}，g∈{16.32}；
[0154]
·
参数集-23：n＝256，l＝2，m＝2,，η1＝η2＝η3＝2，q≤7681，t1＝t2＝4， g∈{4,8，16}；或n＝256，l＝2，m＝2,η1∈{1，4}，η2＝η3∈{4，1}，q≤7681，t1∈{3，4,5}，t2∈{4，5}，g∈{4，8，16}；
[0155]
·
参数集-24：n＝512，l＝2，m＝2,η1＝η2＝η3＝2,q≤7681， t1∈{2,3}，t2∈{2，3}，g∈{4，8，16，32,64}；或n＝512， l＝2，m＝2,η1∈{1，4}，η2＝η3∈{4，1},q≤7681，t1∈{0，1，2,3,4},t2∈{0，1，2,3,4}， g∈{2，4,8，16,32，64,128,256}；
[0156]
·
参数集-25：n＝256，l＝4，m＝4,，η1＝η2＝η3＝2，q≤7681， t1∈{0，1，2},t2∈{0，1，2}，g∈{4,8，16,32，64}；或n＝256， l＝4，m＝4,η1∈{1，4}，η2＝η3∈{4，1},q≤7681，t1∈{0，1，2,3,4},t2∈{0，1，2,3,4}， g∈{2，4,8，16,32，64,128,256}。
[0157]
本发明的第四方面，所述方法包括：当m≥3，或者使用共识方式-3 或4或5或6或7，或者使用上述共识方式-1的con或rec共识机制且使用上述压缩和解压缩方式-3或4或5，或者使用上述共识方式-2的con 或rec共识机制且使用上述压缩和解压缩方式-1或2或3或4，参数设置如下：
[0158]
·
参数集-26：n＝256，l＝2，η1＝2，η2＝η3＝12，，q≤7681，t1＝3，t2＝4，，g＝8；
[0159]
·
参数集-27：n＝256，l＝3，η1＝1，η2＝η3＝4，，q≤7681，t1＝4，t2＝4，g＝16；
[0160]
·
参数集-28：n＝512，l＝2，η1＝2，η2＝η3＝8,，q≤12289，t1＝2或3，t2＝3 或4，g＝16；
[0161]
·
参数集-29：n＝256，l＝2，η1＝η2＝η3＝2，q≤3329，t1＝0，t2＝2或3， g＝8；
[0162]
·
参数集-30：n＝256，l＝3，η1＝η2＝η3＝2，q≤3329，t1＝0，t2＝2或3， g＝16；
[0163]
·
参数集-31：n＝256，l＝4，η1＝η2＝η3＝2，q≤3329，t1＝0，t2＝1或2， g＝32；
[0164]
·
参数集-32：n＝256，l＝4，m＝4，η1＝η2＝η3＝2，q≤7681，t1＝0，t2＝2， g＝32或64或128；
[0165]
·
参数集-33：n＝256，l＝4，m＝4，η1＝η2＝η3＝1，q≤3329，t1＝0，t2＝1或 2，g＝32或64或128或256；
[0166]
·
参数集-34：n＝256，l＝4，m＝4，η1＝η2＝η3＝1，q≤3329，t1＝1，t2＝1，g＝1024或512或2048；
[0167]
·
参数集-35：n＝256，l＝4，m＝4，η1＝η2＝η3＝1，q≤3329，t1＝0，t2＝0， g＝8或16或32或64或128或256。
[0168]
如上所述的方法，在具体计算两个多项式的乘法时，需要对多项式进行快速数论变换(ntt变换)。所述参数中，部分参数无法进行完整的传统ntt变换，可采取新型的ntt变换进行处理。
[0169]
发明方法的创新性和困难性说明
[0170]
发明方法在实际应用中的有效性(包括计算效率、带宽、错误率等) 严重依赖具体参数的选取。而这些参数的选取需要综合考量大量因素，并需要编程测试。其中一个重要的难点是错误率的分析。发明方法的具体错误率依赖于所采用的压缩函数compress和解压缩函数decompress，以及所采用的具体的非对称共识机制中的con和rec算法。据我们所知，针对不同压缩方式和共识机制的错误率分析目前并不完备，特别是针对发明方法的砍比特方式的压缩方式的精确错误率和程序都是空白。
[0171]
我们回顾一下，本发明的第二方面所描述的压缩方式：
[0172][0173]
首先对本发明的第三方面所描述的共识机制(方式2)证明如下引理：
[0174]
引理1.1记则共识算法要满足正确性，要求参数满足条件(2d+2)
·
2＜q
·
(1-2/g)。
[0175]
证明：根据定义，存在ε1∈{0,1/2}，ε2∈(-1/2,1/2]，使得 v＝g(σ2+qk2/2+ε1)/q+ε2+θ
·
g。代入k1的表达式可得
[0176][0177]
所以存在ε3∈(-1/2,1/2]使得
[0178][0179]
根据假设，存在和δ∈[-d,d]使得σ2＝σ1+θ'
·
q+δ。所以，我们有
[0180][0181]
要达到正确性，则要求|2
·
δ/q+2
·
(ε1+ε3)/g+2ε2/g|≤2d/q+2/q+1/g＜1/2即可。整理可得(2d+2)
·
2＜q
·
(1-2/g)。
[0182]
当q＝7681，g＝8时，计算可得这种共识应满足的条件为 d＜1439.6875＜1440。
[0183]
我们记∈1＝a
·
x1+e
1-decompress(compress(a
·
x1+e1))，∈2＝a
t
·
x2+e2-ꢀ
decompress(compress(a
t
·
x2+e2))，则图中的σ
1-σ2为
[0184][0185]
当采用本发明的第二方面的方式1的压缩函数时，有
[0186][0187]
当采用本发明的第二方面的方式4的压缩函数时，有
[0188][0189]
这里，我们有
[0190][0191]
记ε2＝a
t
·
x2+e
2-decompress(compress(a
t
·
x2+e2))，ε1＝a
·
x1+e1ꢀ-
decompress(compress(ax1+e1))，则
[0192][0193]
这里，ε'∈[-1/2,1/2)，
[0194][0194]
当|err|＜q/4-1/2时，可以正确解密。
[0195]
主要分析n＝256,l＝3这一组参数的错误率，这也是发明方法实际应用中常用的参数。
[0196]
下面我们对比两种情况下的误差表达式。
[0197]
情况l：采用本发明的第二方面的方式4压缩并采用本发明的第三方面的方式2共识机制，原始加密算法的误差为识机制，原始加密算法的误差为其中，其中，这里的y1对应为t1不等零情况的decompress(compress(ax1+e1))，或对应t1等零情况的ax1+e1。根据模lwe假设将c
v
的系数看成服从分布 (在python代码中，
)。当满足条件 err＜q/4时可以正确解密，即为err＜1920.25(满足err＜q/4-1/2即可正确解密)。
[0198]
情况2：采用本发明的第二方面的方式4压缩并采用本发明的第三方面的方式1共识机制，则误差为当 err＜d＜(q(1-2/g)/2-1)/2＝1439.7时，共识算法满足正确性，即能正确解密。
[0199]
定义：我们称一个上的离散概率分布d是中心对称的，如果-d＝d，即离散概率分布d是中心对称的，如果对任意的x
←
d，pr[x]＝pr[-x]均成立。
[0200]
注意到，上述误差的计算都可以看做是在上进行的，没有经过mod 运算。错误率的计算逻辑是：在模lwe的假设下，将ε1,ε2,ε
v
的系数看做是服从分布：x-decompress compress x,然后通过枚举，用程序算出x1,x2,e1,e2,e
σ
服从的中心二项分布列和ε1,ε2,ε
v
对应的分布列。再枚举计算e
i-ε
i
,(e
i-ε
i
)x
j
的分布列。注意到(e
i-ε
i
)x
j
的每一个系数由l
·
n个独立服从此分布的系数的加和。
[0201]
我们使用δ来表示则对应的情况2的错误率计算是估计分布δ取值大于(q(1-2/g)/2-2)/2＝1439.1875的概率，情况1 是计算δ-ε
v
取值大于q/4＝1920.25的概率。现在来重新回顾一下引理的证明，采用情况1的共识算法，k1的表达式为
[0202][0203]
我们实际上可以换一种共识上界的证明，注意到按照我们的符号表示，σ2为rec的输入，我们可以假设σ2是均匀分布的。此时，
[0204][0205]
这里，根据假设服从分布：当||σ
2-σ
1-ε
v
||
∞
＜q/4-1/2时，可以推出k1＝k2。引理的证明中相当于取了ε
v
的绝对上界来推出的|σ
1-σ2|的上界d应满足的条件。但是，ε
v
是一个概率分布。以具体的参数为例，ε
v
的取值在 [-480,480]之间，以一定的概率取每个值。这样，|σ
1-σ2|小于1440时，一定可以推出k1＝k2。但是，1440＜|σ
1-σ2|＜1920时，由于ε
v
的存在，也有一定的概率使得k1＝k2。在实际应用中，也是根据模lwe假设计算的，服从一定的概率分布的变量。所以，采用直接从lwe解密角度的方式来计算误差，是更直接的算出变量服从的概率分布，然后枚举计算解密错误发生的概率。这样，相当于更直接的计算，将概率“分散”了。对于不同的参数(主要是)，ε
v
的分布不同。根据上面的推理和观察，我们进行编程实验，并做大量的测试来确定发明方法的具体参数取值，以取得最佳的效率、带宽和错误率效果。