一种降低时延违约概率的传输方法

1.本发明属于移动通信领域，尤其涉及一种降低时延违约概率的传输方法。


背景技术：

2.随着社会的不断发展，用户对数据的传输速率和传输质量有了更高的要求。而多输入多输出技术能在相同的时频资源上服务多个用户，既能减弱信道相关性对系统性能的影响，又可获得更高的传输速率，故受到了广泛关注。
3.相对于只传输一种信息的传统多用户广播方案，速率分拆技术能够减轻用户间干扰带来的影响，提升系统自由度、频谱效率、能量效率和可靠性，降低信道状态信息反馈开销，是当前无线网络通信的热点技术之一。
4.目前5g场景中的低时延要求的短包通信以及mimo-rsma技术的联合研究都引起了极大关注，有关rsma优于sdma和noma的有限块长度编码已有初步研究可以证明。但是短包通信中的系统性能与长包通信有很大的不同，因此短包通信会对mimo-rsma系统的性能产生很大的影响，为了更好的将此系统应用在未来5g的发展中，基于mimo-rsma系统的短包通信的时延研究是非常有意义的。


技术实现要素：

5.为了提高无线通信网络的时延性能，本发明公开了在单小区下行传输链路中一种降低时延违约概率的传输方法。
6.本发明实施例提供了如下技术方案：
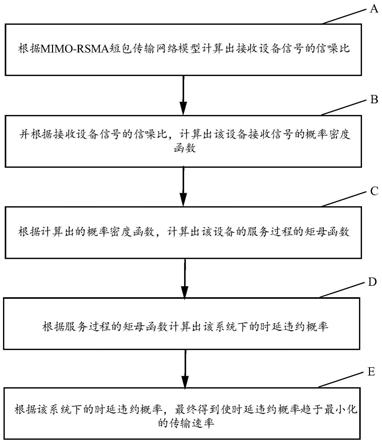
7.mimo-rsma短包传输网络模型中最小化时延违约概率下的传输速率的计算，其特征在于，包括如下步骤：
8.步骤a，根据mimo-rsma短包传输网络模型计算出接收设备信号的信噪比；
9.步骤b，根据接收设备信号的信噪比，计算出该设备接收信号的概率密度函数；
10.步骤c，根据计算出的概率密度函数，计算出该设备的服务过程的矩母函数；
11.步骤d，根据服务过程的矩母函数计算出该系统下的时延违约概率；
12.步骤e，根据该系统的时延违约概率，最终可以得到使时延违约概率趋于最小化的传输速率。
13.其中，步骤a具体包括：
14.a1，根据mimo-rsma短包传输模型，基站发送的信息需要拆分为公有信息和私有信息，通过信道估计得出基站与用户k之间的信道为hk∈cm×1，故公有信息的sinr为私有信息的sinr为其中是公共数据流sc的预编码器， p1＝,...,＝pk＝hk(h
khhk
)-1
分别是数据流s1,...,sk的预编码器，pc、pj表示给公共数据流和私有数据流分配的发射功率。其中k表示用户数，且k∈k。
15.其中，步骤b具体包括：
16.b1，根据接收设备公有信息的信噪比，分别求得其分子分母的概率密度函数为其中其中m表示基站发射天线数，γ(k)＝(k-1)！；
17.b2，根据公有信息信噪比分子分母的概率密度函数，若要求整体分式的概率密度函数(pdf)，需要求分子与分母的联合pdf，其联合pdf表示为其中t＝z+1；
18.b3，同理求得私有信息的信噪比为
19.其中，步骤c具体包括：
20.c1，矩母函数的串联性质具体表示为其中分别为公有部分信噪比与私有信号信噪比概率密度函数的矩母函数，且其中θ、xc为公有部分的系统参数，x为系统整个传输过程的时间参数；
21.c2，根据公有部分信噪比的pdf求其矩母函数，即其中、n为短包传输的块长度，v
c,k
＝1-(1+γ
c,k
)-2
为公有信息部分的信道色散，且q-1
为q函数的逆函数，ε
c,k
为公有信息的误块率，γ(s,x)、γ(s,x)分别为上不完全伽马函数和下不完全伽马函数；
22.c3，同理，根据私有部分信噪比的pdf求其矩母函数为其中εk为私有信息的误块率，其中vk＝1-(1+γk)-2
为私有信息部分的信道色散，且
[0023][0024]
c4，服务过程的矩母函数为
[0025][0026]
其中，步骤d具体包括：
[0027]
d1，假定到达过程服从泊松分布，其矩母函数为其中λ为数据平均到达速率；
[0028]
d2，根据布尔不等式存在时延违约概率为其中， d为时延参数，假设时延违约概率范围为(0,1]，则
[0029]
其中，步骤e具体包括：
[0030]
e1，为了便于分析，固定私有信息部分的传输速率，则根据时延违约概率表达式可以将时延违约概率约束下的传输速率表示为其中其中表示均值符号；
[0031]
e2，取关于r
c，k
的二阶导数具体表达式为根据ε
c,k
(n,γ
c,k
)的近似表达式可得可得大于0，其中c(γ
c,k
)＝log2(1+γ
c,k
)，如此可判断
[0032]
e3，令根据q函数的性质即
其中对进行简化为其中
[0033]
e4，最终可以得出最小化时延违约概率时系统传输的速率为其中为抛物线圆柱函数。
[0034]
与现有技术相比，上述技术方案具有以下优点：
[0035]
本发明利用了随机网络演算(snc)等分析工具，分析了下行单小区用户接收端信噪比的pdf，并且根据此pdf，能够求出其服务过程的矩母函数，从而计算出其时延违约概率，最终求出使得时延违约概率趋于最小化时的系统传输速率的值。
附图说明
[0036]
为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。
[0037]
图1为本发明一个实施例所提供的一种基于mimo-rsma短包传输网络中使时延违约概率趋于最小化的传输方法。图2为本发明一个实施例所提供的一种基于mimo-rsma短包传输网络 中使时延违约概率趋于最小化的传输方法应用的系统模型示意图。
具体实施方式
[0038]
正如背景技术部分所述，如何降低无线通信网络中传输时延的违约概率为本领域人员亟待解决的问题。
[0039]
本发明的核心思想在于，利用了随机网络演算(snc)等分析工具，分析了下行单小区用户接收端信噪比的pdf，并且根据此pdf，能够求出其服务过程的矩母函数，从而计算出
其时延违约概率，最终求得使其时延违约概率趋于最小化的传输速率。
[0040]
参见图1，本发明实施例提供单小区下行传输链路中一种降低时延违约概率的传输法，具体为mimo-rsma短包传输网络模型中最小化时延违约概率下的传输速率的计算，所述方法包括：
[0041]
步骤a，根据mimo-rsma短包传输网络模型计算出接收设备信号的信噪比；
[0042]
步骤b，根据接收设备信号的信噪比，计算出该设备接收信号的概率密度函数；
[0043]
步骤c，根据计算出的概率密度函数，计算出该设备的服务过程的矩母函数；
[0044]
步骤d，根据服务过程的矩母函数计算出该系统下的时延违约概率；
[0045]
步骤e，根据该系统的时延违约概率，最终可以得到使时延违约概率趋于最小化的传输速率。
[0046]
其中，步骤a具体包括：
[0047]
a1，根据mimo-rsma短包传输模型，基站发送的信息需要拆分为公有信息和私有信息，通过信道估计得出基站与用户k之间的信道为hk∈cm×1，故公有信息的sinr为私有信息的sinr为其中是公共数据流sc的预编码器， p1＝,...,＝pk＝hk(h
khhk
)-1
分别是数据流s1,...,sk的预编码器，pc、pj表示给公共数据流和私有数据流分配的发射功率。其中k表示用户数，且k∈k，
[0048]
其中，步骤b具体包括：
[0049]
b1，根据接收设备公有信息的信噪比，分别求得其分子分母的概率密度函数为其中其中m表示基站发射天线数，γ(k)＝(k-1)！；
[0050]
b2，根据公有信息信噪比分子分母的概率密度函数，若要求整体分式的概率密度函数(pdf)，需要求分子与分母的联合pdf，其联合pdf表示为其中t＝z+1；
[0051]
b3，同理求得私有信息的信噪比为
[0052]
其中，步骤c具体包括：
[0053]
c1，矩母函数的串联性质具体表示为其中分别为公有部分信噪比与私有信号信噪比概率密度函数的矩母函数，且其中θ、xc为公有部分的系统参数，x为系统整个传输过程的时间参数；
[0054]
c2，根据公有部分信噪比的pdf求其矩母函数，即
其中、n为短包传输的块长度，v
c,k
＝1-(1+γ
c,k
)-2
为公有信息部分的信道色散，且q-1
为q函数的逆函数，ε
c,k
为公有信息的误块率，γ(s,x)、γ(s,x)分别为上不完全伽马函数和下不完全伽马函数；
[0055]
c3，同理，根据私有部分信噪比的pdf求其矩母函数为其中εk为私有信息的误块率，其中vk＝1-(1+γk)-2
为私有信息部分的信道色散，且
[0056][0057]
c4，服务过程的矩母函数为
[0058][0059]
其中，步骤d具体包括：
[0060]
d1，假定到达过程服从泊松分布，其矩母函数为其中λ为数据平均到达速率；
[0061]
d2，根据布尔不等式存在时延违约概率为其中， d为时延参数，假设时延违约概率范围为(0,1]，则
[0062]
其中，步骤e具体包括：
[0063]
e1，为了便于分析，固定私有信息部分的传输速率，则根据时延违约概率表达式可以将时延违约概率约束下的传输速率表示为
其中其中表示均值符号；
[0064]
e2，取关于r
c,k
的二阶导数具体表达式为根据ε
c,k
(n,γ
c,k
)的近似表达式可得可得大于0，其中 c(γ
c,k
)＝log2(1+γ
c,k
)，如此可判断
[0065]
e3，令根据q函数的性质即其中对进行简化为其中
[0066]
e4，最终可以得出最小化时延违约概率时系统传输的速率为其中为抛物线圆柱函数。
[0067]
与现有技术相比，上述技术方案具有以下优点：
[0068]
本发明利用了随机网络演算(snc)等分析工具，分析了下行单小区用户接收端信噪比的pdf，并且根据此pdf，能够求出其服务过程的矩母函数，从而计算出其时延违约概
率，最终求出使时延违约概率趋于最小化时的系统传输速率的值。
[0069]
本发明的技术方案中，在针对密集型物联网业务信息传输与处理中无法准确保证业务的及时处理，提出了一个时延性能的指标——时延违约概率；根据密集型物联网业务传输系统的模型，计算出接收设备的信噪比；根据计算的信噪比求其pdf，根据其pdf计算出服务过程的矩母函数。这样，利用矩母函数的串联性质，可以求出时延违约概率，最终求出使得时延违约概率最小化的系统传输速率。这里利用随机网络演算对网络性能进行分析，相比排队论，随机网络演算(snc)更适合用于一般的到达过程和服务过程，而不需要假设到达过程和服务过程符合某种特殊分布函数，因此，随机网络演算在分析网络性能方面比排队论更具优势，被广泛用于网络数据流的传输性能分析。且相比于确定性网络演算，snc能够取得一个更符合实际网络的性能边界。
[0070]
下面详细介绍本技术的技术方案：
[0071]
考虑一个下行链路传输的单小区，小区基站装有m根发射天线，基站同时在瑞利衰落信道上向k个单天线用户发送消息(如图2)，为满足低时延需求，用短包进行通信，采用速率拆分方案，基站将要发送给用户k(k∈k)的消息wk分为公有部分和私有部分(w
k0
,w
k1
)，所有用户信息的公共部分使用共享的码本编码为公共流sc，而私有部分各自编码为私有流sk，则基站要传输的全部数据流为：
[0072][0073]
数据流经过线性预编码器进行预编码，其中是数据流sc的预编码器，p1,...,pk分别是数据流s1,...,sk的预编码器，且私有流经过zfbf预编码，同时以匹配波束成形的方式对公共流进行预编码，最后将私有流与公共流进行线性叠加后基站发射信号为：
[0074][0075]
假设发射机处知道完美的csi，基站发射功率为p，分配给公共消息功率为pc＝p(1-t)，基于注水算法给私有消息分配功率为p1,...pk，t∈(0,1]表示功率分配因子。公共流的预编码器是以的匹配波束成形。且私有流预编码器p1＝,...,＝pk＝h(hhh)-1
。表示信道衰落矩阵。用户k 的接收信号为：解码过程如下：首先通过将私有流视为噪声解码公共流，用户k在通过sic消除解码后的公共流后，将其他用户的私有流视为噪声来解码其私有流。其中hk∈cm×1是基站与用户k之间的信道，x∈cm×1是发送信号，tr(pph)≤p，是接收端具有单位方差的加性高斯白噪声。
[0076]
信噪比分布的推导：
[0077]
利用短包进行传输，用于传输的信道编码的块长度相当小，有限块长度的信道编码将导致显著的性能损失，发射机可以通过选择低于信道容量的速率来降低传输错误的概率，但是传输错误不能忽略。因此当给定用户的错误概率以及块长度时，下行链路传输的可实现的公共速率表示为：
[0078][0079]
其中，v
c,k
表示信道色散v
c,k
＝1-(1+γc)-2
，q-1
(
·
)表示的逆函数，γ
c,k
表示用户uk的公共信号与干扰加噪声比。为了确保所有的用户都能解码公共流，公有信息的sinr为：
[0080][0081]
γc＝min(γ
c,1
,...,γ
c,k
)
[0082]
私有速率为：
[0083][0084]
其中，vk＝1-(1+γk)-2
，γk表示用户uk的私有信号与干扰加噪声比。
[0085][0086]
a:针对求其pdf
[0087]
由于公共流采用匹配波束成形预编码为了更好的分析，将γc重写为：
[0088][0089]
考虑到已有参考文献表明服从γ(k,1)的分布，令则 x的
概率密度函数可以表示为：
[0090][0091]
其中，γ(
·
)表示伽马函数，其表达式为：
[0092][0093]
接下来求分母的pdf：
[0094]
根据现有文献可知服从自由度为2k的卡方分布，则z的概率密度函数可以表示为：
[0095][0096]
这里，x与z为相互独立的随机变量，已知信噪比γc与x、z的关系为：
[0097][0098]
若要求信噪比的概率密度函数，则需要求的pdf和x与的联合概率密度。
[0099]
由于之前已求出z的概率密度函数，则令z+1＝t，随机变量t的pdf为：
[0100][0101]
因为x与t相互独立,故可以求的pdf为：
[0102][0103]
采取以下方法求γc的pdf的闭合表达式：直接利用现有文献的参考公式(如下)：
[0104][0105]
则可以根据上式将积分处理为：
[0106][0107]
其中，k'＝k+1，w(
·
)是惠特克函数。
[0108]
则可以得出最终γc信噪比的pdf为：
[0109][0110]
又因
[0111][0112][0113][0114]
已知贝塔函数存在
[0115]
根据合流超几何函数1f1(k；2k+1；γc)在当2k为整数时消失，可以得出：
[0116][0117]
则最终公共信息的概率密度函数为：
[0118][0119]
b:针对私有求其pdf
[0120]
根据现有文献可以得知其服从自由度为2(m-k+1)的卡方分布。则其 pdf为：
[0121][0122]
随机网络演算求时延违约概率：
[0123]
利用矩母函数求解时延问题，主要考虑业务的到达过程和服务过程：
[0124]
到达过程：
[0125]
①
假设数据流到达过程遵循平均速率为λk的泊松分布，则其表示为：
[0126][0127]
则到达过程的矩母函数形式为：
[0128][0129]
服务过程：
[0130]
将公有信息和私有信息的服务看做是两个串联的过程
[0131]
则公有部分服务过程存在：则服务过程为： s
c,k
＝r
c,k
ny，同理，所以我们可以推导出公有部分服务过程中的矩母函数变换如下：
[0132]
已知：则存在公有信息的矩母函数为：
[0133][0134]
详细化简部分：
[0135]
其积分部分为
[0136][0137]
令
[0138]
其中
[0139]
同理，私有部分的矩母函数变换如下：
[0140][0141]
将其积分部分化为：
[0142]
[0143][0144][0145]
至此，两部分的矩母函数已全部推出，假定两部分相互独立，则根据矩 母函数的定义，则服务总过程为：则同样将求出的上式代入。
[0146]
可以得到时延违约概率为：
[0147][0148][0149]
可见，本技术利用了随机网络演算(snc)等分析工具，分析了下行单小区用户接收端信噪比的pdf，并且根据此pdf，能够求出其服务过程的矩母函数，从而计算出其时延违约概率，最终求得使其时延违约概率趋于最小化的传输速率。
[0150]
本说明书中各个部分采用递进的方式描述，每个部分重点说明的都是与其他部分的不同之处，各个部分之间相同相似部分互相参见即可。
[0151]
对所公开的实施例的上述说明，使本领域专业技术人员能够实现或使用本发明。对这些实施例的多种修改对本领域的专业技术人员来说将是显而易见的，本文中所定义的一般原理可以在不脱离本发明的精神或范围的情况下，在其它实施例中实现。因此，本发明将不会被限制于本文所示的实施例，而是要符合与本文所公开的原理和新颖特点相一致的最宽的范围。