一种运动平台矢量脱靶量参数估计修正方法与流程

本发明涉及矢量脱靶量测量测量技术领域，特别是一种运动平台矢量脱靶量参数估计修正方法。

背景技术：

现代战争中，导弹由于其具有精确的制导性能而倍受青睐，对于各种新型制导武器的研制日趋重要。然而对于制导武器性能的测试却存在高成本、难度大、实验条件难以满足等问题。因此采用目标上安装脱靶量测量设备来检测武器性能。制导武器的性能一般在弹与靶的遭遇段得到比较集中的体现，因此在靶场试验中，通过测量制导武器在遭遇段的运动参数(包括标量脱靶量参数(作用距离L₀，导弹运动速度v₀，脱靶量r₀)和矢量运动参数(脱靶点坐标，导弹运动轨迹的方位角与俯仰角)，可以确定导弹在接近目标这一过程中在空中的运动轨迹，从而检验制导武器的精度，评定其性能的优劣。

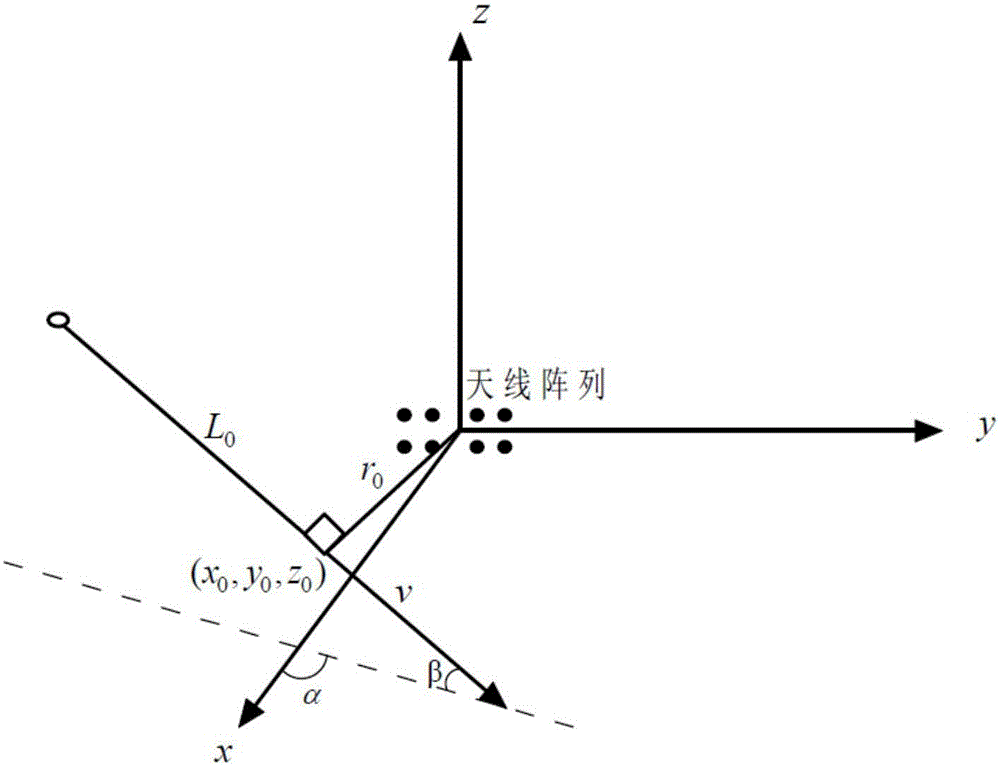
矢量脱靶量测量实际上是要测量弹靶遭遇段导弹的运动轨迹。假设弹靶遭遇段目标作匀速直线运动，导弹运动轨迹与测量雷达收发天线阵的关系如图1。在图中定义的系统测量坐标中，设靶标位于坐标原点。显然，目标的直线运动轨迹可由五个参数唯一确定：脱靶点的坐标(x₀,y₀,z₀)；弹道运动轨迹与oxy平面的夹角既弹道倾角β；运动轨迹方向角既弹道偏角α。加上目标运动速度v和目标脱靶时刻t₀(或起始时刻目标到脱靶点的距离L₀)，目标在空间运动的整个时间历史就可唯一确定。因此，矢量脱靶量测量的任务就是设法测量这些运动参数：

标量脱靶量测量原理是弹靶交会过程中目标回波的多普勒频率随时间而变化，变化规律由导弹与目标的相对速度v、标量脱靶量r₀、脱靶时刻t₀(起始时刻目标到脱靶点的距离L₀)决定。对应不同的参数，多普勒频率随时间的变化规律也不同。因此，只要测得交会过程目标回波多普勒频率随时间的实际变化曲线，采用最优化方法对其作最优拟合，就可得到标量脱靶量参数。

设脱靶量测量设备安装在靶标上，导弹相对靶标作匀速直线运动，设导弹运动速度为v，导弹运动轨迹与靶标最近点到靶标的距离即标量脱靶量为r₀，时间参考点t＝0时刻，导弹与脱靶点的距离为L₀。若脱靶量测量设备发射波长为λ，根据多普勒效应，则导弹反射回到接收天线的回波信号多普勒频率变化为：

只要测得交会过程目标回波的多普勒频率随时间的实际变化曲线就可以根据下面公式，求解如下非线性最小二乘问题。

矢量脱靶量的测量原理是通过测量弹靶交会过程中空间位置不同的接收天线接收的目标回波相位差随时间变化曲线，通过与运动轨迹模型的相位差最优拟合，估计出矢量脱靶量参数。

假设脱靶点的坐标为(x₀,y₀,z₀)，M个接收天线的坐标为(x_i,y_i,z_i)，其中i＝1,2,3....M，导弹的弹道偏角和弹道倾角分别为α和β，t时刻导弹的轨迹的坐标为(x(t),y(t),z(t))。由于导弹与各接收天线的斜距不同，不同的接收天线在同一时刻接收到的目标回波存在相位差，第i与第j路天线接收到的多普勒回波的相位差为：

其中r_i(t)和r_j(t)分别是第i和第j路在t时刻导弹到接收天线的瞬时距离：

其中,

显然，不同的接收天线接收的目标回波相位差随时间变化的规律与脱靶点的坐标(x₀,y₀,z₀)、弹道偏角α、弹道倾角β以及{v,L₀,r₀}有关，导弹运动速度为v，导弹运动轨迹与靶标最近点到靶标的距离即标量脱靶量为r₀，时间参考点t＝0时刻，导弹与脱靶点的距离为L₀。因此，只要测得交会过程目标回波的M-1条相位差随时间的实际变化曲线，在获得{v,L₀,r₀}的测量结果后，可构造如下准则函数

式中和分别为在t_i时刻目标反射回波的理论相位差和实际估计相位差。通过求解如下约束非线性优化问题就可获得目标运动轨迹的矢量脱靶量参数{(x₀,y₀,z₀),α,β}的估计：

矢量脱靶量参数估计需要获得目标回波到各路接收天线间的相位差，而由回波数据估计出的多普勒信号的相位差实际上包括两部分：一部分是目标回波到达两路接收天线间的时间差产生的相位差；另一部分是由接收机相位不一致产生的相位差。显然，前者含有目标运动轨迹的有用信息，后者，则需要从回波相位差的估计值中去除。多普勒频率和天线间回波相位差的估计是数据处理的核心部分，估计性能的好坏直接影响到脱靶量参数的准确性。由于目标运动过程中多普勒频率和回波相位差不断变化，要获得准确的瞬时多普勒频率和瞬时回波相位差，就会面临很多困难。

载体晃动是我们不得不面对的问题。如将矢量脱靶量测量装置安装在靶船目标上，用于检测弹道导弹或者反舰导弹攻击靶船时导弹的各项性能参数，即计算导弹与靶船交汇过程中的矢量脱靶量参数。由于靶船受到海况等其他因素的影响，会导致船只有较大的起伏，会导致各个天线接收通道观测到的回波信号相位具有较大的误差，从而影响矢量脱靶量参数的估计值，使得最终估计得到的导弹性能参数不可靠，导致实验的失败。因此，对运动平台矢量脱靶量参数估计的修正显得尤为重要。

对于此问题，通常是选择在做实验时保持载体稳定或者具有较小的晃动，从而尽量降低载体晃动对观测数据的影响。然而，微小的扰动也会带来较大的误差，在后面将会给出扰动对误差的分析，而且稳定的环境下实验数据也不具有代表性；

另一种解决思路是在载体上安装4个GPS天线，通过4个天线实时测出各个仿真时刻载体的偏航角、俯仰角、横滚角。然后将矢量脱靶量测量设备的天线置于三轴转台上，通过实时控制系统接收GPS或惯导系统测得的载体摆动数据，解算成相应的转台伺服修正控制指定，实时控制转台来抵消载体的运动，消除载体运动带来的回波数据测量误差。

以上两种方法均是以“维稳”为指导思想，第一种方法对实验要求太苛刻，而且不具有实验代表性；第二种方法则实现难度较大，如果载体运动频率太快，由于测量数据分析、处理、伺服接收控制参数均存在一定的延时，因此实时性难以保证，难以修正载体带来的观测误差。

技术实现要素：

本发明要解决的技术问题为：通过从数据估计的目标函数出发，去补偿载体运动带来的数据误差，将载体平台的运动等效于导弹运动的航迹数据，并采用改进的非线性参数估计算法，实现运动平台矢量脱靶量参数的估计修正。

本发明采取的技术方案具体为：一种运动平台矢量脱靶量参数估计修正方法，包括以下步骤：

S1，通过安装于运动平台上的测量装置，以测量周期Δt₁对运动平台的偏航角α_k、俯仰角β_k和横滚角数据θ_k进行测量获取，测量值α_k、β_k、θ_k即第k个测量时间段kΔt₁获取到的运动平台姿态数据；

S2，设置多个天线接收通道用于接收目标回波数据，分别对各天线接收通道接收到的目标回波数据进行处理，包括：对目标回波数据进行分时处理，即按照不同目标运动速度设置相应的数据处理帧长度Δt，基于数据处理帧长度对目标回波数据进行处理，进而得到对应各天线接收通道的目标回波信号随时间变化的多普勒频率信息f_di(t_k)和相位信息i代表通道序号，即接收天线的编号；

S3，基于各个通道对应的多普勒频率信息数据和对应的时间数据，分别构造相应的目标函数：

其中，t＝0时刻导弹与脱靶点的距离L₀，导弹运动速度v，和标量脱靶量r₀为待估计参数，t_n＝n×Δt，n为数据帧数，为t_n时刻对应的多普勒测量值，λ为测量装置的发射信号波长；

通过求解下式：

分别得到对应各个通道的L₀，v，r₀的估计值，再对所有通道得到的各估计值取平均值，得到标量脱靶量参数测量值；

S4，对于各个通道得到的相位信息对不同通道之间进行相位做差，得到不同通道之间的相位差数据l和i分别代表第l和第i个接收通道；

S5，基于步骤S3得到的标量脱靶量参数依据矢量估计约束条件：

构造目标参数空间，其中x₀，y₀，z₀，α，β为矢量脱靶量测量参数，由空间几何关系，可知矢量目标参数满足如下关系：

-r₀≤x₀,y₀,z₀≤r₀，0≤α≤π,0≤β≤π/2，

在上述范围内，对于x₀,y₀,z₀和α,β分别以一定的间隔来撒点，得到可行解空间构成的解的结合；

S6，基于步骤S1获得的运动平台状态测量数据，结合步骤S4得到的相位差数据，构造矢量参数估计的目标函数，以对运动平台的运动进行补偿：

定义P＝Δt₁/Δt，按照运动平台数据测量周期Δt₁对矢量参数估计的目标函数进行分时建模，以在每个时间段，对各个天线接收通道的天线坐标位置进行修正；

建立的分时目标函数为：

其中，M,N代表天线接收通道的个数，L为目标回波数据的分时处理总帧数，α,β,x₀,y₀,z₀为待估计的矢量脱靶量参数，为对步骤S4中得到的相位差数据按照运动平台测试周期进行分时处理后的数据，其中t_km＝(kP+m)Δt＝nΔt，k为运动平台数据测量的周期标号，m代表在每一次运动平台测量周期内数据的时间标号，m＝n(mod P)，mod代表同余运算，

为匹配模板函数，其中含有待估计矢量未知参数，构造过程如下：

6-1基于步骤S3得到的标量脱靶量参数L₀，v，r₀的估计值，构造未修正的含矢量估计参数的匹配模板函数：

上式中，x_i,y_i,z_i为第i个接收天线的坐标；

6-2在运动平台运动数据的各测量周期内，根据下式对天线坐标位置x_i,y_i,z_i进行修正：

M＝M_z×M_y×M_x (66)

上式中，x_i',y_i',z_i'即修正后的天线坐标位置；

6-3将6-1中，式(63)和式(64)中的x_i,y_i,z_i换成修正后的x_i',y_i',z_i'，即得到重构的修正后的匹配模板函数将修正后的匹配模板函数代入分时目标函数式(61)，即得到重构的分时目标函数；

S7，对步骤S6重构的分时目标函数进行优化，对步骤S5中得到的可行解空间中的各个解，分别计算其适应度对，即对应的函数值大小，找出适应度最好即函数值最小的点，也即全局次优解，将该解作为非线性估计函数fmincon的初始值，进而寻找全局次优解附近的最优解，得到全局最优解，作为参数估计的最优值，即得到要估计的矢量脱靶量相关参数。其中非线性估计技术为目前使用很成熟的非线性估计算法，利用最小二乘估计算法作为其核心算法，通过最速梯度下降法等相关成熟的最优值搜索算法来寻找误差最小时对应的待估计参数的值，得到全局最优解，该方法为目前成熟使用的算法。

由于矢量脱靶量构造的目标函数形式比较复杂，估计的参数较多，普通的非线性估计算法都得不到满意的结果，采用遗传算法与非线性估计算法结合的方法进行估计，遗传算法具有较好的全局寻优性，普通的非线性估计算法则有较好的局部最优性。因此可利用先通过遗传算法找到全局极优值，再以此作为普通非线性算法的初值进行估计，寻找全局最优的思想来实现。但仿真表明，采用该种方法需要大量的种群和遗传代数，需花费较大的运算量，且由于种群的构造、交叉、遗传、变异都具有一定的随机性，并不能保证能得到最优估计值。

而本发明秉承先寻找全局最优，再寻找局部最优的思想，但对上述思想进行了改进，抛弃了利用遗传算法寻找局部最优，而利用约束条件：

来均匀撒点，寻找局部最优，再将局部最优值作为非线性估计函数fmincon的初始值进行迭代寻找全局最优。

进一步的，本发明步骤S1中，通过安装在运动平台上的GPS系统或惯导系统实时测量运动平台的姿态数据。

为了使得数据处理的结果更准确可靠，本发明步骤S2中，用于接收目标回波数据的通道数量为8个。

步骤S2中，对各天线接收通道接收到的目标回波数据首先进行过门限检测，得到包含目标回波的有效数据段，然后对过门限检测后得到的目标回波数据进行分时处理检测。门限可根据试验对象的数据特征进行设置，门限检测可滤除无效数据段，进一步提高数据处理结果的相关性和可靠性。

优选的，本发明中，对于经过门限检测后得到的目标回波数据，按照不同目标运动速度，分别设置对应的数据处理帧长度：目标运动速度为100m/s以下时，数据处理帧长度为6～10ms；目标运动速度为100～300m/s时，数据处理帧长度为2～4ms；目标运动速度为300～800m/s时，数据处理帧长度为0.5～2ms；目标运动速度为1000m/s以上时，数据处理帧长度为0.5ms以下。高速目标通常采用滑窗处理来增加数据有效帧数。

在进行相位做差时，理论上每两个通道之间都需要做一次相位差，但实际应用时，只需要使用其中部分相位差数据即可。优选的，本发明步骤S4中，对于各个通道得到的相位信息选取其中一个通道的相位信息数据，分别与其它各通道之间进行做差，得到其它各通道与所选取通道之间的相位差数据如可选取第一通道的相位数据作为参考，与其它七个通道分别做差，得到相应的相位差数据。

本发明的有益效果为：本发明不将目光锁定在运动平台的“维稳”上，而是从数据估计的目标函数出发，采用等效思想完成数据修正，以补偿载体运动带来的数据误差，即运动平台产生的运动等效作用于导弹运动的航迹数据，进而得到修正后的矢量脱靶量参数估计结果。在对重构的目标函数进行寻优时，首先采用遗传算法进行全局寻优，然后采用非线性散发进行局部寻优，避免了较大的运算量，运算的效率提高同时寻优效果较好。

仿真结果和实验结果都表明，采用本发明的估计算法，不仅在求解时间上大大缩短，而且改进了估计结果的不稳定性，使得每次估计都能得到最优估计值。

附图说明

图1所示为导弹运动轨迹与测量雷达收发天线阵的关系示意图；

图2所示为本发明方法流程示意图。

具体实施方式

以下结合附图和具体实施例进一步说明。

矢量脱靶量测量设备通常装在运动平台上，如靶船，因此导弹攻击目标的仿真实验中，载体不可避免的会受到一些外界因素而产生晃动，幅度可大可小，晃动频率可能很慢，也可能很快，对测量数据带来较大的影响，从而导致最终的参数估计结果具有较大的误差，使得实验结果不具备参考性，无法对导弹的性能进行评估，还可能导致实验的失败，因此需要对数据进行修正。载体晃动对估计数据的影响如表1和表2所示：

表1 载体运动对标量脱靶量参数估计的影响

表2 载体运动对矢量脱靶量参数估计的影响

表1和表2中，标量测量值和矢量测量值下，括号内为真值。

由表一可以看出，随着载体运动角度的变化，标量脱靶量参数受到的影响很小，基本可以忽略不计。

由表二数据可以看出，随着载体运动角度表达，矢量脱靶量参数的误差也逐渐增大，当载体的晃动角度大于10°时，带来的位置误差已经超多10％，角度误差更大。

本发明给出了一种纯数据的修正方法，该方法通过对参数估计过程中的目标函数和估计出的结果进行补偿，完成对估计数据的修正。

步骤S1，首先通过安装在运动平台上的GPS系统或惯导系统实时测量得到运动平台的偏航角、俯仰角、横滚角数据；

步骤S2，通过八个接收通道接收目标回波数据，根据实验对象设置相应的检测门限，对个通道的回波信号进行门限检测，得到包含目标回波的有效数据段。根据目标种类的不同，对目标有效回波数据进行分时处理，即按照不同的目标运动速度，设置不同的数据处理长度。通常100m/s以下的目标数据长度为6～10ms，100～300m/s为2～4ms,300～800m/s为0.5～2ms,1000m/s以上为0.5ms以下，高速目标通常采用滑窗处理来增加数据有效帧数。根据设置的数据帧长度对各个通道接收到的目标回波数据进行处理，以得到对应各个通道的目标回波信号随时间变化的多普勒频率信息和相位信息；

每次数据处理得到一个回波信号多普勒频率变化函数f_di(t_k)，参考式(21)，i为通道序号，即接收天线的编号，t_k为测量时刻；

通过对整个目标数据段进行处理，得到各个通道目标多普勒频率信息，并根据第一通道各帧多普勒对应的频率点，找到相应的索引，即将第一通道的数据按帧处理，对各帧数据做chirpZ变换将数据变换到频域，找出幅度最大点对应的下标，该下标即为索引。以此索引为参考，取出各帧数据中该索引对应的相位值参考式(3)和式(4)、(5)：

一般是对各个接收通道的每一帧数据进行FFT处理，通过找到频域数据幅度最大值对应的标号，并以该标号作为参考去找到其他接收通道数据FFT变换后对应的相位值，得到各个接收通道的目标回波信号随时间变化的多普勒频率信息f_di(t_n)和相位信息

步骤S3，基于各个通道对应的多普勒频率信息数据和对应的时间数据，构造相应的目标函数：

其中，L₀，v，r₀为待估计参数，t_n＝n×Δt，Δt为帧处理时长，为t_n时刻对应的多普勒测量值。通过求解：

得到对应的各个通道的L₀，v，r₀的估计值，再对八个通道的数据区平均，得到本次实验测量的标量脱靶量参数测量值；

步骤S4，对于各个通道得到的相位信息t_k＝k×Δt，i为通道序号，两两通道之间进行相位做差，得到不同通道之间的相位差，理论上每两个通道之间都需要做一次相位差，实际应用中，只需要使用其中部分相位差数据即可，本发明中采用第一通道的相位数据位参考，其他七个通道均与第一通道相位做差，得到对应的相位差数据

步骤S5，利用步骤S3中得到的标量脱靶量参数及其脱靶量运动的几何关系，得到矢量估计约束条件

其中x₀，y₀，z₀，α，β为矢量脱靶量测量参数。

依据上述约束条件，构造目标参数空间，由空间几何关系，易知矢量目标参数满足如下关系：

-r₀≤x₀,y₀,z₀≤r₀，0≤α≤π,0≤β≤π/2，

在上述关系范围内，对于x₀,y₀,z₀和α,β分别以一定的间隔来撒点，得到可行解空间构成的解的集，在本次实验中，x₀,y₀,z₀以0.5为间隔撒点，α,β以5°为间隔撒点，在结合约束条件，去掉不符合要求的参数点，形成新的可行解的点集。

步骤S6：基于步骤S1获得的运动平台运动数据重新构造目标函数，以对运动平台的运动进行补偿。我们已经由惯导系统测得各个时间运动平台载体的姿态角数据，结合步骤S4中得到的相位差数据，构造矢量参数估计的目标函数。

在构造目标函数过程中，需要对平台的运动进行补偿。我们已经由惯导系统测得各个时间运动平台载体的姿态角数据，因此在目标函数构造过程中，对相应的匹配模板进行分时处理，按照惯导的测试数据时间间隔对匹配模型进行分时设计。

假设惯导测试数据周期为Δt₁，在本次实验中，采用的惯导系统数据测量周期为10ms，步骤二中使用的数据处理帧长度为Δt，则P＝Δt₁/Δt，按照惯导测试数据的周期对目标函数进行分时建模，在每个时间段，根据惯导的测试数据，对八个接收天线的坐标位置进行修正，分时建立匹配模型函数，从而构建分时目标函数如下：

其中，M,N为天线通道的个数，在实际中，我们采用8个接收天线通道，L为目标回波数据的分时处理总帧数，α,β,x₀,y₀,z₀为待估计的矢量脱靶量参数，为步骤S4中得到的相位差数据进行按平台测试周期分时后的数据，l,i代表第l和第i个接收通道。

t_km＝(kP+m)Δt₂＝nΔt₂，k代表运动平台数据测试的周期标号，m代表在每一次运动平台测试周期内数据的时间标号，n是数据帧数，m＝n(mod P)，mod代表同余运算；

为匹配模板函数，其中含有待估计矢量未知参数，构造过程如下：

6-1基于步骤S3得到的标量脱靶量参数L₀，v，r₀的估计值，构造未修正的含矢量估计参数的匹配模板函数：

即得到未修正的匹配函数上式中，x_i,y_i,z_i为第i个接收天线的坐标；

6-2在每个惯导测量周期内，即目标函数对应的第k个时间段内，我们已经由惯导系统测得该时段的运动平台的姿态数据偏航角(α_k)、俯仰角(β_k)和横滚角数据(θ_k)，则根据下式，在各测量周期内，对天线接收坐标x_i,y_i,z_i数据进行修正：

M＝M_z×M_y×M_x (66)

上式中，x_i',y_i',z_i'即修正后的天线坐标位置；6-3将6-1中，式(63)和式(64)中的x_i,y_i,z_i换成修正后的x_i',y_i',z_i'，即得到重构的修正后的匹配模板函数将修正后的匹配模板函数代入分时目标函数式(61)，即得到重构的分时目标函数；

步骤S7，对步骤S6重构的分时目标函数进行优化，对步骤S5中得到的可行解空间中的各个解，分别计算其适应度对，即对应的函数值大小，找出适应度最好即函数值最小的点，也即全局次优解，将该解作为非线性估计函数fmincon的初始值，进而寻找全局次优解附近的最优解，得到全局最优解，作为参数估计的最优值，即得到要估计的矢量脱靶量相关参数。

由于矢量脱靶量构造的目标函数形式比较复杂，估计的参数较多，普通的非线性估计算法都得不到满意的结果，采用遗传算法与非线性估计算法结合的方法进行估计，遗传算法具有较好的全局寻优性，而普通的非线性估计算法则由较好的局部最优性。因此采用先通过遗传算法找到全局极优值，在以此作为普通非线性算法的初值进行估计，寻找全局最优的思想来实现。仿真表明，采用该种方法需要大量的种群和遗传代数，需花费较大的运算量，且由于种群的构造、交叉、遗传、变异都具有一定的随机性，并不能保证能得到最优估计值。

在本发明中，我们秉承先寻找全局最优，在寻找局部最优的思想，对该算法进行改进，抛弃了遗传算法寻找局部最优，而利用约束条件：

来均匀撒点，寻找局部最优。

表3 采用本发明的方法修正后的矢量脱靶量参数

由表3的数据可知，采用本发明的数据修正方法，对数据进行修正后，载体晃动对估计数据带来的误差基本已经消除，剩下的误差均是由估计带来的。

仿真结果和实验结果都表明，采用改进后的估计算法，不仅在求解时间上大大缩短，而且改进了估计结果的不稳定性，使得每次估计都能得到最优估计值。