利用心率回复率量测体能状态的方法与装置与流程

本发明关于一种量测体能状态(例如：心肺功能/自律神经调节状态)的方法及装置，特别是关于一种利用心率回复率量测体能状态(例如：心肺功能/自律神经调节状态)的方法或装置。
背景技术：
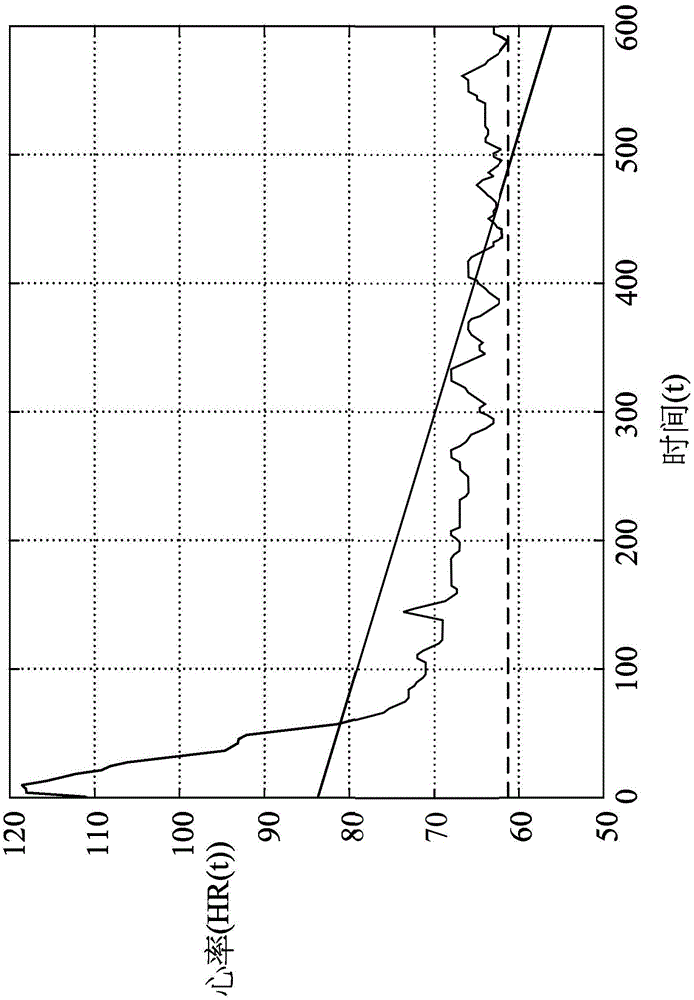
：哈佛登阶测验是1943年由美国哈佛大学疲劳研究所Brouha教授所提出的，是以登阶运动后的心率恢复率来判定心肺机能的一种简便而有效的方法。当初的设计是受测者在规定时间内，以一定的上下登阶频率反复运动。所述台阶阶高20时(50.8公分)，登阶频率为每分钟上下踏台30次，运动时间通常为3分钟，最长为5分钟。在运动结束后，记录登阶测验运动后休息时1分到1分30秒、2分至2分30秒与3分至3分30秒的三个心跳数，以恢复期心跳数计算体能指数。心肺耐力指数的计算方式，是以运动的时间(秒数)乘以100为分子，三次心跳的和乘以2为分母，以判定人体心肺耐力优劣、于身体负荷下的调整与恢复能力，指数越高的人，肌耐力越好，心肺能力越强。经许多研究验证运动后心率回复(heartraterecovery)是自律神经调控心率及心肺功能的重要表现，而运动后心率回复率(heartraterecoveryrate)评估体能状态的重要指标之一，例如心肺功能与自律神经调控，且与心血管疾病的死亡率下降有正相关。在回复期中，心率是依循非线性关系下降，在现有技术中却均采用线性回归方式计算运动后心率回复率，如图1所示，而且是在运动后1-5分钟，以非连续续性方式量测心率来计算运动后心率回复率，因此量测精确度不佳。因此，有必要发展出一种在运动后持续一段时间(如10-15分 钟)以连续性方式量测心率且以非线性回归方式计算运动后心率回复率的方法或装置，而更准确地评估体能状态(例如：心肺功能/自律神经调节状态)。技术实现要素：本发明目的在于提供一种量测体能状态(例如：心肺功能/自律神经调节状态)的方法与装置，其利用非线性回归方程式计算运动后心率回复率，改善现有技术中以线性回归方程式计算运动后心率回复率所产生的不精确的问题。为达上述目的并解决现有技术之缺点，本发明提供一种利用运动后心率回复率量测体能状态(例如：心肺功能/自律神经调节状态)的方法，其包括以下步骤：在一个体运动后量测所述个体在一回复期的心率；根据所述个体的心率，计算所述个体心率的一非线性回归方程式，所述非线性回归方程式中包括一代表所述个体的运动后心率回复率的参数；及根据所述参数决定所述个体体能状态(例如：心肺功能/自律神经调节状态)。在本发明之一实施例中，所述非线性回归方程式包含指数回归方程式或对数回归方程式。在本发明之一实施例中，所述指数回归方程式由以下公式定义：HR(t)＝HRd×C(-K×t)+HRr或是HR(t)＝(HR0-HRr)×C(-K×t)+HRr，其中t为时间，HR(t)为在时间t时的心率，HRr为静止心率，HR0为回复期开始时的心率，HRd为回复期开始时的心率与静止心率之差异，K为所述代表所述个体的运动后心率回复率的参数，C为一常数。在本发明之一实施例中，一运动后心率回复半衰期与代表所述个体的运动后心率回复率的参数K的关系由以下公式定义：其中t1/2为所述运动后心率回复半衰期。在本发明之一实施例中，所述对数回归方程式由以下公式定义：HR(t)＝a ×logct+R，其中t为时间，HR(t)为在时间t时的心率，R为与静止心率相关的参数，a为所述代表所述个体的运动后心率回复率的参数，C为一常数。在本发明之一实施例中，所述常数C为自然常数e。在本发明之一实施例中，所述个体运动为登阶运动。在本发明之一实施例中，在所述个体运动后量测所述个体在一回复期的心率的步骤包括在所述个体运动后连续性地量测所述个体在一回复期的心率。为达上述目的并解决现有技术之缺点，本发明提供一种利用运动后心率回复率量测体能状态(例如：心肺功能/自律神经调节状态)的装置，其包括一心率量测单元，用于在一个体运动后量测所述个体在一回复期的心率，并输出一数位化心率讯号；一心率处理单元，连接所述心率量测单元，用于接收所述数位化心率讯号，并根据所述个体的心率，计算所述个体心率的一非线性回归方程式，所述非线性回归方程式中包括一代表所述个体的运动后心率回复率的参数，及根据所述参数决定所述个体体能状态(例如：心肺功能/自律神经调节状态)。在本发明之一实施例中，所述非线性回归方程式包含指数回归方程式或对数回归方程式。在本发明之一实施例中，所述指数回归方程式由以下公式定义：HR(t)＝HRd×C(-K×t)+HRr或是HR(t)＝(HR0-HRr)×C(-K×t)+HRr，其中t为时间，HR(t)为在时间t时的心率，HRr为静止心率，HR0为回复期开始时的心率，HRd为回复期开始时的心率与静止心率之差异，K为所述代表所述个体的运动后心率回复率的参数，C为一常数。在本发明之一实施例中，一运动后心率回复半衰期与代表所述个体的运动后心率回复率的参数K的关系由以下公式定义：其中t1/2为所述运动后心率回复半衰期。在本发明之一实施例中，所述对数回归方程式由以下公式定义：HR(t)＝a×logct+R，其中t为时间，HR(t)为在时间t时的心率，R为与静止心率相关的参数，a为所述代表所述个体的运动后心率回复率的参数，C为一常数。在本发明之一实施例中，所述常数C为自然常数e。在本发明之一实施例中，所述个体运动为登阶运动。在本发明之一实施例中，所述心率量测单元用于在所述个体运动后连续性地量测所述个体在一回复期的心率。在本发明之一实施例中，所述装置为一穿戴装置。附图说明图1是根据现有技术中以线性回归方程式量测运动后心率回复率的示意图。图2是根据本发明一实施例中利用运动后心率回复率量测一个体体能状态(例如：心肺功能/自律神经调节状态)的方法的步骤示意图。图3是根据本发明一实施例中以指数回归方程式量测运动后心率回复率的示意图。图4是根据本发明一实施例中以对数回归方程式量测运动后心率回复率的示意图。图5至第5C图是三个不同个体在进行相同运动强度的运动持续相同期间后量测其心率资料，再根据本发明的方法所计算出的指数回归方程式图形。图6是根据本发明一实施例中以指数回归方程式量测运动后心率回复率的另一示意图。图7是根据本发明的量测体能状态(例如：心肺功能/自律神经调节状态)的装置的结构示意图。具体实施方式请参考图2，其为根据本发明一实施例中利用运动后心率回复率量测一个体体能状态(例如：心肺功能/自律神经调节状态)的方法的步骤示意图。所述利用运动后心率回复率量测一个体体能状态的方法，包括以下步骤：步骤S100：在所述个体运动后量测所述个体在一回复期的心率，步骤S200：根据所述个体的连续性心率，计算所述个体心率的非线性回归方程式，所述非线性回归方程式中包括一代表所述个体的运动后心率回复率的参数，及步骤S300：根据所述参数决定所述个体体能状态(例如：心肺功能/自律神经调节状态)。在本发明一实施例中，所述个体所进行的运动包括任何能提高心率之运动，例如登阶、爬山、跑步、走路、球类运动、舞蹈、游泳、瑜珈或划船等，以上所述之运动仅为实施范例，不应以此限制本发明。在本发明一实施例中，本发明量测所述个体在一回复期的心率的方法包括侦测心电讯号、心音及脉搏等。侦测心电讯号通常是利用至少一对电极进行侦测，而侦测心电讯号的可以分为侵入式或非侵入式的方法。当本发明之方法实施在植入式医疗装置时，可以利用侵入式心电讯号量测方法，当本发明之方法实施在穿戴式装置时，可以利用非侵入式心电讯号量测方法。基于穿戴式装置的便利性，在以下的实施列中，本发明皆是利用穿戴式装置以非侵入式的方法量测心电讯号，然这不表示其他的心率量测方法不可行。以上所举例之心率量测方法仅为实施范例，不应以此限制本发明。本发明中所述恢复期(recoveryperiod)为一个体在运动结束后心率开始下降至静止心率(restingheartrate)的一段期间。所述恢复期从运动结束后即开始，当心率下降至静止心率后结束。静止心率是指一个体在无运动状态下的心率，此时心脏在每单位时间内泵送最少量的血液，对人类而言，静止心率一般为每分钟40-100下，而视个体与运动习惯而有差异，通常有运动习惯之个体的静止心率较没有运动习惯的心率低，代表其心脏每次搏动可以泵送较 多血液。而本发明的运动后心率回复率(heartraterecoveryrate)是指在恢复期中个体的心率下降速率。量测所述个体的心率可以在恢复期前期、中期、后期或是整段恢复期中进行一段期间，所述期间可以为1、2、3、4、5、6、7、8、9、10、11、12、13、14、15、16、17、18、19、20、21、22、23、24、25、26、27、28、29或30分钟等，或是1-30分钟内所包含的所有数值范围，而在本发明中优选为10-15分钟或3-5分钟，以上所述之量测期间仅为实施范例，不应以此限制本发明。本发明中以连续性方式量测心率是指在所述期间内量测心率多次，且每次量测的时间间隔不超过10秒，在本实施范例中，是每隔1秒量测一次心率。这与现有技术中每隔数十秒或是一分钟才量测一次的非连续性的量测方式有所不同，在现有技术中由于量测次数少，所以精确度不佳，也因此只能使用线性回归方法计算运动后心率回复率，造成更大的误差。在回复期中，心率是依循非线性关系下降，在现有技术中却均采用线性回归方式计算运动后心率回复率，因此量测准确度不佳。而本发明中式以非线性回归方式计算运动后心率回复率的方法或装置，而更准确地评估体能状态(例如：心肺功能/自律神经调节状态)。本发明的非线性回归方式是指根据从所述个体量测的心率资料，计算出所述心率资料的非线性回归方程式。所述非线性回归方程式包括指数方程式、对数方程式、三角函数方程式、椭圆形方程式、圆形方程式、二次方程式、三次方程式及多次方程式等。因此，所有非线性方程式都可应用在本发明内。特别是，指数方程式、对数方程式更能符合回复期中心率下降的曲线，其中以指数方程式为最佳模式，因此在本说明书中以指数方程式、对数方程式作为实施范例，但不应以此限制本发明。请见图3，其为本发明一实施例中以指数回归方程式量测运动后心率回 复率的示意图，其横轴为时间，纵轴为心率，曲折的曲线代表个体的心率资料，平滑的曲线代表根据所述心率资料所计算的指数回归方程式。指数回归方程式公式定义如下：[通式一]HR(t)＝HRd×C(-K×t)+HRr，或是[通式二]HR(t)＝(HR0-HRr)×C(-K×t)+HRr，或是其中t为时间，HR(t)为在时间t时的心率，HRr为静止心率，HR0为回复期开始时的心率，HRd为回复期开始时的心率与静止心率之差异，K为所述代表所述个体的运动后心率回复率的参数，C为一常数，在本实施例中常数C为一自然常数e。请见图4，其为本发明一实施例中以对数回归方程式量测运动后心率回复率的示意图，其横轴为时间，纵轴为心率。对数回归方程式公式定义如下：[通式三]HR(t)＝a×logct+R其中t为时间，HR(t)为在时间t时的心率，R为与静止心率相关的参数，a为所述代表所述个体的运动后心率回复率的参数，C为一常数，在本实施例中常数C为一自然常数e。运动后心率回复半衰期(half-life)t1/2，即HR0降低一半HRd所需的时间，其与代表所述个体的运动后心率回复率的参数K的关系由以下公式定义：[通式四]在本实施例中常数因为C为一自然常数e，因此运动后心率回复半衰期t1/2与代表所述个体的运动后心率回复率的参数K的关系可由以下公式定 义：[通式五]因为K为所述代表所述个体的运动后心率回复率的参数，K越大则代表回复期心率降低速度越快，所以可以利用K的大小决定个体的体能状态(例如：心肺功能/自律神经调节状态)。请参考图5A至第图5C，其为三个不同个体在进行相同运动强度的运动，持续相同期间后量测其心率资料，再根据本发明的方法所计算出的指数回归方程式图形。其横轴为时间，纵轴为心率，曲折的曲线代表个体的心率资料，平滑的曲线代表根据所述心率资料所计算的指数回归方程式。请参考表1，其显示三个不同个体在进行相同运动强度的运动，持续相同期间后的心肺功能量测结果，其分别记录了回复期开始时的心率HR0、所述代表所述个体的运动后心率回复率的参数K、运动后心率回复半衰期t1/2以及代表准确度的判定系数R值(CoefficientofDeterminationorR-square)。在表1中，个体二的参数K最大，代表其运动后心率回复率最快，体能状态(例如：心肺功能/自律神经调节状态)最佳，因此在图5A中其心率的指数回归方程式图形下降得最陡峭，而其运动后心率回复半衰期t1/2也最短。在表1中，个体一的参数K最小，代表其运动后心率回复率最慢，体能状态(例如：心肺功能/自律神经调节状态)最差，因此在图5C中其心率的指数回归方程式图形下降得最平缓，而其运动后心率回复半衰期t1/2也最长。表一：HR0(次/分)K(秒-1)T1/2(秒)R值(判定系数)个体一133.211110.0118158.6942196.15％个体二126.355670.0197735.0604696.12％个体三129.320460.0150146.1797091.74％心率非线性回归方程式的实现方法：可以使用各种程式语言或是统计软体来计算心率非线性回归方程式，例如C++、Java、Python甚至是Excel、SAS，在本发明知中是利用Python来实现心率非线性回归方程式，然而必须注意的是所述的程式语言或统计软体仅为实施范例，不应以此限制本发明。首先利用Python寻找「最佳自然对数衰退方程式」，一般是采用最小平方法。「最小平方法」是一种数学优化技术，其通过最小化误差的平方和寻找数据的最佳函数匹配。目前市面上有许多最小平方法功能的程式库(1ibrary)可提供选用，所以在本实施范例中并不自行另外实现所述程式库，而是选用其中的一种适当的程式库。在本发明的实施范例中，是使用Python的SciPy程式库(SciPylibrary)中的curve_fit函数(curve_fitfunction)，curve_fit函数具有趋近(fit)的功能。此外并利用回调函数(callbackfunction)，其中的公式即为「最佳自然对数衰退方程式」。可透过将回调函数(callbackfunction)给予此curve_fit函数，curve_fit函数会根据时间与心率资料对回调函数(callbackfunction)中的「最佳自然对数衰退方程式」重复趋近(fit)以求得最符合心率资料的曲线方程式。其具体实现的程式码如下：[通式六]deffitFunc(t，a，b，c)：returna*np.exp(-b*t)+cfitParams，fitCovariances＝scipy.curve_fit(fitFunc，t，data)fitFunc即为回调函数(callbackfunction)，需要输入四个参数(arguments)： 分别为时间t、回复期开始时的心率与静止心率之差异a、所述代表所述个体的运动后心率回复率的参数b、静止心率c。而curve_fit函数(curve_fitfunction)输入三个参数(arguments)：分别为fitFunc、时间t、心率资料HR。其他运算细节应以及其他衰退方程式得实现方法是本领域通长技术人员可根据以上说明书内容推得而知，在本说明书中不再赘述。此外，必须注意的是以上所述的心率非线性回归方程式的实现方法，仅为一实施范例，不应以此限制本发明。线性回归方程式与非线性回归方程式的精确度比较：在此比较运用线性回归线与非线性回归线量测运动后心率回复率heartraterecoveryrate)的精确度。在本实施例比较中，所述的非线性回归线包括指数回归线与对数回归线。在本实施例比较中，是以判定系数(CoefficientofDetermination)或称R值(R-square)作为精确度的判定标准。判定系数是在回归分析中，用来了解在自变数X与依变数Y所建立的回归模式中，Y所呈现出来的讯息有多少是由X所影响而决定的。在本实验中，自变数X即为时间t，而依变数Y即为心率HR，所以R值在此所表示的为t对HR有多少的决定性。R值最高为1最低为0，越高越好，越高就代表本发明所限定的自变数对依变数有更大的决定性，也代表其他未知的自变数对依变数的影响更小。也同时可以解释，推导出来的自然对数衰退方程式与实测的曲线有多少的密合度(conformity)。因此，R值越高就代表本发明中此参数K对心率曲线有更大的意义。R值是根据以下公式计算出来的：[通式七]即为总平方合(totalsumofsquares)：残差平方合(residualsumofsquares)：也可以利用Python计算出R值，其具体实现的程式码如下：[通式八]forelemindata：SSTo+＝np.square(elem-AVG)SSResid+＝np.square(elem-fitFunc(t[index]，fitParams[0]，fitParams[1]，fitParams[2]))print″R-square″，1-SSResid/SSTo以上所述的R值计算方法，仅为一实施范例，不应以此限制本发明。请见图1与图3，其分别为根据现有技术中以线性回归方程式计算运动后心率回复率的示意图，以及本发明一实施例中以指数回归方程式计算运动后心率回复率的示意图。其横轴为时间，纵轴为心率，曲折的曲线代表个体的心率资料，直线代表根据所述心率资料所计算的线性回归方程式，平滑的曲线代表根据所述心率资料所计算的指数回归方程式。图中所述实施例的线性回归方程式的R值为0.4458，指数回归方程式的R值为0.9612。请见表2，其显示各种回归方程式的R值平均值，非线性回归方程式的R值显著较高，其中指数回归方程式精确度(0.8852)远高于线性回归方程式(0.5743)。其理由如下：图3中，回复期前期的心率迅速降低，回复期后期的心率逐渐水平地趋近于静止心率(restingheartrate)，而指数回归线密切地密合心率资料的曲线。相反地，在图1中，习用线性回归线仅能在回复期后期松散地符合心率资料的曲线，而在回复期前期严重地偏离心率资料的曲线，因此指数回归方程式的精确度远高于线性回归方程式。请见图6与图4，其分别为本发明一实施例中以指数回归方程式量测运动后心率回复率的另一示意图，以及本发明一实施例中以对数回归方程式量测运动后心率回复率的一示意图。其横轴为时间，纵轴为心率，曲折的曲线代表心率资料，平滑的曲线代表根据所述心率资料所计算的非线性回归方程。当前第1页1 2 3