用于控制应用的滚动时域状态初始化器的制作方法

申请人：加利福尼亚大学董事会。

本发明是在由国立卫生研究院(NIH)授予的资助编号为DP3DK094331和ROIDK085628的政府支持下进行的。政府对本发明拥有一定的权利。

背景技术：

我们的研究和开发的总体目标是用于向患有1型糖尿病(T1DM)的人自动输送胰岛素的人工胰腺(AP)(参见例如Cobelli等人[2009]，Harv ey等人[2010]，Cobelli等人[2011]，Zisser[2011]，Doyle III等人[2014])。特别地，考虑通过连续葡萄糖监测器(CGM)(Hovorka[2006])感测葡萄糖(用于反馈的测量)的AP。AP的关键要素是进行有效和安全的基于算法的胰岛素剂量分配的反馈控制法则。例如，已经提出了基于模型预测控制(MPC)的血糖控制器(Parker等人[1999]，Hovorka等人[2004]，M agni等人[2009]，Breton等人[2012]，Turksoy等人[2013])。我们的团队越来越关注于开发所谓的区域-MPC策略(Grosman等人[2010，2011]，van Heusden等人[2012]，Gondhalekar等人[2013，2014]。

实施每个MPC的关键要素是表征由其进行预测的初始条件的机制。存在两种主要方法。在基于一般的状态-空间模型的MPC中，通常采用状态判定器，例如Luenberger观察器或卡尔曼滤波器(参见例如Levine[2011])。或者，当使用输入-输出模型，例如具有外源性输入(ARX)的自回归模型时，初始条件最简单地由过去的输入和输出值组成(即使当使用该系统的状态-空间表示法时)。甚至对于基于ARX模型的预测控制，状态判断方法也受到我们的青睐，因为它使用于调节噪声抑制能力的处理(ha ndle)简单。在例如Magni等人[2007]中，采用输入-输出方法，其中指出“这种输入-输出MPC方案的主要优点是不需要观察器”。两个递归线性状态判断器(该类包括Luenberger-观察器和标准卡尔曼-滤波器)和输入-输出初始化是直接实施的，但有缺点。该项工作解决了这些缺点中的至少三个。初始化MPC预测的设备此后被简称为状态判断器，而不管其模型类别。所提供的状态判断器适用于一般的状态-空间模型以及输入-输出模型两者。

这里解决的第一个缺点是传感器重新校准不能很好地适应现有的状态判断器。CGM信号经受(至少)两种类型的噪声。首先，存在高频随机噪声，其影响在一定程度上可以通过调整递归状态判断器的增益来补救(Bequette[2004])。然后存在低频漂移，也被称为传感器偏差，这源于CGM传感器增益的缓慢波动特性和传感器位置的生理学变化。通过利用比CGM更准确的传感器进行不定时(sporadic)血糖测量来校正这些低频干扰，例如在维护血糖测量装置的时间点测量。随后相对于基准测量值“重新校准”CGM。在接收到重新校准的数据点时，递归状态判断器可以照常更新其状态判断，或者可能采用比使用CGM数据更新时更高的增益，以反映更高的置信度。Kuure-Kinsey等人[2006]提出了一种相关的方法，其用于基于卡尔曼滤波的估算葡萄糖，并且这样的方法看来对于估算葡萄糖的目的而言工作良好。然而，出于在MPC中状态初始化的目的，该策略是不理想的，因为在重新校准之后，状态判断器经历活跃的动态期(a period of lively dynamics)。这些积极的响应(energetic response)可能导致无意义的预测，会导致严重的过度输送(over-delivery)。因此，在我们的控制器中，大的重新校准之后是胰岛素输注速率被限制到患者的基础速率(basal rate)的时间段。这似乎是浪费，因为重新校准是将高保真数据引入系统。优选地，系统可以利用该数据并且在重新校准之后运行得更好，而不必经历有意的暂时性中断(crippling)。

第二个缺点是异步CGM数据不能被容纳在当前的递归状态判断器中，其中“异步”意味着CGM的采样周期可能不是固定的，并且此外，CGM和控制器运行更新的时间瞬时可能不相同。我们的控制器(物理控制器和离散时间预测模型)基于T＝5min的采样周期。典型的CGM大部分时间具有相同的采样周期。然而，CGM可能在高不确定性的时间期间延迟它们的输出。此外，一旦重新建立数据传输时，传感器和仪表之间的通信中断就导致延迟的测量更新。如果实际采样周期被延长，则基于固定采样周期的状态判断器可能过度估计数据的变化速率，并且不能补偿控制器更新时间与最新CGM测量之间的延迟。两个问题导致MPC预测以这样的方式初始化，即它们偏离(veer off)CGM轨迹，可能导致不适当的胰岛素输送。

第三个缺点是由于装置模型(plant-model)不匹配，基于模型的递归状态判断器不总能实现无偏移的判断(offset-free estimate)，即使在稳态下，当状态相对于模型、输入和测量的输出不被容许时。可以通过增加判断器增益来部分补偿偏移，但是这不期望地导致对高频噪声的响应性增加。

我们提供了克服前述三个缺点的状态判断策略。我们的解决方案基于滚动时域优化，而不是递归判断器。它的灵感来自但不等于滚动时域判断的普通观念(Rawlings和Mayne[2009])。所公开的方法进行优化以将连续时间函数拟合到CGM数据。通过在函数定义内包括葡萄糖输出值而非其导数的不连续性，直接适应传感器重新校准。重要的是，不连续性的大小不需要规定，而是通过优化来识别。数据拟合利用CGM时间戳(time-stamp)和控制器调用时间，因此异步数据采样被自然地处理。在优化之后，正好在控制器模型的采样周期T处对拟合的函数采样，忽略重新校准的不连续性，以合成输出轨迹。结合历史输入数据，并假设可观察性，构建当前模型状态以反映没有偏移的拟合输出轨迹。所公开的策略可以与卡尔曼滤波器或其他信号处理技术结合，以预处理CGM数据；然而，为了简洁，示例基于使用原始CGM数据。

技术实现要素：

成功的人工胰腺系统中的一个关键组件是控制算法，该系统被设计为将1型糖尿病人的血糖浓度维持在正常血糖区域(80-140mg/dL)内，该控制算法自动地指示待管理的胰岛素的输送给患有1型糖尿病的受试者。存在很多种控制算法；本发明可应用于或者基于“状态反馈”或者基于具有“自回归”组件的模型的控制策略类形，特别侧重于“模型预测控制”算法。我们的人工胰腺研究小组已设计并测试了用于人工胰腺治疗1型糖尿病的多种状态反馈模型预测控制策略。

一方面，对于其计算所基于的控制器，本发明基于血糖测量来表征模型状态(用于状态反馈控制器)或模型输出轨迹(用于基于自回归模型的控制器)，以便促进对血糖水平的优越控制。从目前可购得的血糖传感器获得的血糖测量具有使用于表征模型状态的当前机制产生退化或不适当的控制行为的属性。本发明的一个实施例是：1)适应血糖传感器重新校准，以便当重新校准传感器时，促进优越的控制；2)利用传感器测量的时间戳，以便当传感器测量经受不规则的采样间隔时，促进优越的控制；3)除了测量时间戳之外，利用控制器时间戳，以便当控制器和传感器更新时间不同步时，促进优越的控制。此外，与现有技术不同，本发明不依赖于模型，因此补偿了由于不可避免的装置模型不匹配导致的不良效应。

本发明可以与基于状态反馈或自回归模型的任何反馈控制策略一起使用。其与模型预测控制算法特别相关的原因是，由于预测控制器的行为是基于整个预测的轨迹，相比于仅依赖于当前模型状态，适当地初始化模型状态需要的是增加的优先级。简言之，利用预测控制，需要设置指向正确方向的预测。

一方面，本发明通过将连续时间函数拟合应用到所获得的血糖传感器测量，并随后在模型的采样周期处对拟合的连续时间函数采样，以便合成模型输出轨迹而起作用。这样，异步和不一致的传感器定时的影响被消除。通过在重新校准发生的那些时间瞬时包括拟合函数的值而非其导数的不连续性来适应传感器重新校准。重要地，在采样过程中不连续性被忽略。对于状态反馈控制，结合所保存的控制输入轨迹的历史值，从合成的输出轨迹构建当前模型状态。对于基于自回归模型的控制器，可以直接采用合成的模型输出轨迹，代替如当前标准程序的实际输出轨迹。

本发明提供了可并入到进行状态反馈模型预测控制的设备或算法中的状态初始化算法，用于基于血糖测量反馈来优化给1型糖尿病人的胰岛素输送，例如胰岛素泵、连续葡萄糖监测系统或人工胰腺。

本发明在帕多瓦大学/弗吉尼亚FDA公认的代谢模拟器上、和非相关研究的临床数据上、并扩展到计算机中和临床试验进行评估，作为人工胰腺、CGM设备或胰岛素泵的一部分实施。本发明提高了使用基于血糖测量作为反馈的模型预测控制的人工胰腺的能力，将1型糖尿病人的血糖水平维持在正常血糖范围(80-140mg/dL)内。

本发明执行以确保人工胰腺的控制算法正使用准确的过去数据点来进行未来计算，与任何MPC控制算法一起工作，并且可在开环连续葡萄糖监测中提供告警系统。

本发明包括多个其它方面。

一方面，本发明提供了基于模型输出的传感器测量来判断或初始化离散时间状态-空间动力学模型状态的状态判断器的方法，包括将连续时间函数拟合到获取的每个模型输出的传感器测量数据点，并且随后在恰好状态空间动力学模型(该状态-空间动力学模型的状态正在被判断或初始化)的采样周期处对连续时间函数采样，以便经由合成的输出轨迹构建模型状态；其中：

(a)通过允许拟合的函数的值而非导数在重新校准的点处是不连续的来包括传感器重新校准，并且其中，通过优化来识别不连续性的大小，并且其中在忽略重新校准的不连续性的情况下进行拟合函数的采样；

(b)函数拟合采用传感器测量时间戳和状态判断器调用时间，其中：

(i)通过在恰好判断器调用时间处开始的时间向后采样拟合函数来至少部分地减小传感器和状态判断器之间的延迟；以及

(ii)可以适应以不规则时间间隔或者以不是状态正在被判断或初始化的模型的采样周期的时间间隔收集的传感器数据；

(c)状态正在被判断或初始化的模型可以具有输入，并且如果存在输入，则在状态的构建中采用历史输入数据；

(d)模型的状态是可观察或可重构建的；

(e)当状态正在被判断或初始化的模型具有单个输出时，则构建当前模型状态以反映没有偏移的合成输出轨迹，并且当状态正在被判断或初始化的模型具有多个输出时，则采用权衡策略来协调不匹配输出。

这方面和其他方面可以由多种特定的实施例进一步限定，诸如：

其中传感器测量数据用卡尔曼滤波器或其他信号处理技术预处理；

其中所述方法被使用在生物医学应用中的自动化药物输送中，例如用于1型糖尿病或过程控制实施；

其中传感器是连续性葡萄糖监测器(CGM)，并且离散时间状态-空间动力学模型用于预测血糖浓度；

其中所述方法与诸如状态反馈模型预测控制(MPC)律的状态反馈控制律可操作地组合，以进行基于算法的胰岛素给药；

其中所述方法与诸如状态反馈模型预测控制(MPC)系统的状态反馈控制系统可操作地组合以输送胰岛素；

其中所述方法与告警和/或通知系统可操作地组合，其中所述告警和/或通知决策算法采用由离散时间状态-空间动力学模型进行的例如血糖预测的预测，所述离散时间状态-空间动力学模型在其告警和/或通知决策算法中使用模型的状态；和/或

其中所述方法适用于药物输送的医疗设备控制，例如适用于慢性医学病症或治疗的设备，诸如血压控制、血液透析控制、麻醉(例如，深度)控制、帕金森病治疗、白血病治疗、癌症治疗、HIV治疗。

另一方面，本发明提供了用于控制胰岛素输送以治疗1型糖尿病的方法，所述方法包括使用滚动时域优化以将连续时间函数拟合到连续葡萄糖监测(CGM)数据，其中：

(a)通过在函数定义内包括葡萄糖输出值而非其导数中的不连续性来适应传感器重新校准，并且其中通过优化来识别不连续性的大小；

(b)数据拟合采用CGM时间戳和控制器调用时间，从而自然地处理异步数据采样；

(c)在优化之后，在控制器模型的采样周期T处对拟合的函数采样，忽略重新校准的不连续性，以合成输出轨迹；以及

(d)结合历史输入数据，并且假设可观察性，构建当前模型状态以反映没有偏移的拟合输出轨迹。

另一方面，本发明提供了一种用于控制1型糖尿病应用的人工胰腺的胰岛素输送控制的滚动时域状态初始化器的方法，包括：

通过首先经由获取的连续葡萄糖监测(CGM)数据点拟合函数，然后在恰好状态正在被判断的模型的采样周期处对该函数采样来构建模型的状态，其中：

(a)通过允许拟合函数是不连续的来包括CGM传感器重新校准；

(b)传感器和控制器之间的延迟被至少部分地减轻；

(c)可以适应以不规则时间间隔或以不是状态正在被判断的模型的采样周期的时间间隔收集的数据；以及

(d)在判断过程中或期间不使用所述模型，而是判断模型的状态，其中，限制了最终结果的任何装置模型不匹配效应。

另一方面，本发明提供了一种用于治疗1型糖尿病的人工胰腺的模型预测控制(MPC)的方法，包括使用具有传感器重新校准和异步测量的状态判断，其中状态由通过对连续时间函数采样而合成的输出数据来构建，其中通过拟合到测量的连续葡萄糖监测(CGM)传感器数据，并且在传感器重新校准的时间-瞬时包括值而非导数的不连续性，来表征所述函数。

在另外的实施例中可以实践或实现多个方面，包括：

其中所述方法与卡尔曼滤波器或其它信号处理技术组合以预处理CGM数据；

该方法与模型预测控制(MPC)控制算法可操作地组合以输送药物，如胰岛素；和/或

该方法与告警系统可操作地组合，用于诸如开环CGM。

本发明还提供了被编程以实施本主题方法的控制器，以及药物输送系统，其包括被编程以实现主题方法的控制器，可选地包括状态监测系统、药物泵或计量系统和/或待输送药物。

本发明包括基本上如本文所述的算法和药物导向系统，以及所述的特定实施例的所有组合。本说明书中引用的所有出版物和专利申请通过引用并入本文，如同每个单独的出版物或专利申请被具体地并单独地指明通过引用并入本文。尽管为了清楚理解的目的，通过说明和示例相当详细地描述了前述发明，但是本领域普通技术人员将容易明白，在不脱离所附权利要求的精神或范围的情况下，根据本发明的教导，可以进行某些改变和变型。

附图说明

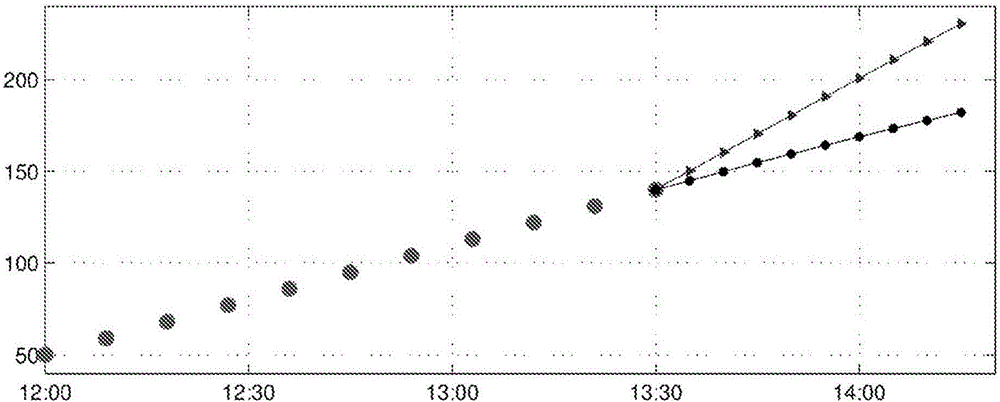
图1是装置模型不匹配的示意。葡萄糖[mg/dL]对比一天中的时间[h]。CGM＝280mg/dL(大点)。低增益线性判断器(三角形)。高增益线性判断器(正方形)。公开的判断器(黑点)。

图2是加长的采样周期的示意。葡萄糖[mg/dL]对比一天中的时间[h]。GCM和MPC同步。CGM(大点)增加率：1mg/dL/min。基于线性判断器的MPC预测(三角形)。所公开的基于判断器的MPC预测(黑点)。

图3是MPC更新和CGM之间4分钟延迟的示意。葡萄糖[mg/dL]对比一天中的时间[h]。CGM(大点)增加率：1mg/dL/min。基于线性判断器的MPC预测(三角形)。所公开的基于判断器的MPC预测(黑点)。

图4是使用MPC和CGM异步的示意。葡萄糖[mg/dL]对比一天中的时间[h]。MPC采样周期：5分钟。CGM采样周期7分钟。CGM(大点)增加率1mg/dL/min。上部：线性判断器，MPC预测(正方形)。下部：公开的判断器，MPC预测(黑点)。

图5是用线性状态判断器重新校准响应的示意，没有安全特性。葡萄糖[mg/dL]或胰岛素[U/5min]对比一天中的时间[h]。MPC和CGM同步：T＝5min。CGM(大点)。MPC预测(三角形)。判断的血糖值(灰色实线)。

图6是利用公开的状态判断器和没有安全特征的重新校准响应的示意。葡萄糖[mg/dL]或胰岛素[U/5min]对比一天中的时间[h]，MCP和CGM同步：T＝5min。CGM(大点)。MPC预测(三角形)。估计的血糖值(灰色实线)。

具体实施方式

用于人工胰腺的MPC以治疗T1DM的具有传感器重新校准和异步测量的状态判断。

提供了新型的状态判断方案，用于在基于连续葡萄糖监测(CGM)反馈的人工胰腺的模型预测控制(MPC)中使用，以治疗1型糖尿病。MPC策略的性能主要取决于预测的初始条件，通常由状态判断器来表征。通常使用的Luenberger观察器和卡尔曼滤波器在大部分时间是有效的，但是受到限制。我们的方法解决了三个特定的限制。首先，以合适的方式适应CGM重新校准和在递归状态判断器中导致高度动态响应的步骤变化。第二，所公开的策略不受异步的CGM测量影响，即既不是固定采样周期，也不是等于控制器的采样周期。第三，该方法不会遭受由于装置模型不匹配引起的偏移。所提供的方法是基于滚动时域优化。

设计；线性时不变胰岛素-葡萄糖模型

采用van Heusden等人的胰岛素-葡萄糖模型[2012]并总结如下。该模型是离散时间、线性时不变(LTI)系统，采样周期T＝5分钟[min]。时间步长索引由i表示。标量装置输入是每个采样周期输送的施用的胰岛素药剂u_IN，i[U]，并且标量装置输出是受试者的血糖值y_BG,i[mg/dL]。装置是围绕稳态的线性化的，假定通过应用受试者特异性、时间依赖性基础输入速率u_BASAL,i[U/h]来实现，并且假定产生稳定状态血糖输出y_s＝110[mg/dL]。

LTI模型的输入u_i和输出y_i定义为：

y_i:＝y_BG,i-y_s

我们分别通过z^-1来表示后向移位算子，通过Y(z^-1)和U(z^-1)来表示输入u_i和输出y_i的时域信号的z变换。从u到y的传递特性由下式描述：

其中，极点p₁＝0.98，p₂＝0.965，所谓的安全系数F＝1.5(无单位，可个性化，但在本文中固定为1.5)，受试者特定总的每日胰岛素量[U]，并且其中常量

用于设置正确的增益，并用于单位转换。1800的项源于用于判断相对于速效胰岛素的输送的血糖下降的“1800原则”(Walsh和Roberts[2006])。

用于控制合成(1)的状态-空间实现是：

x_i+1＝Ax_i+Bu_i (2a)

y_i＝Cx_i (2b)

n＝3

令并注意到等于从顶部到底部翻转的单位矩阵。

注释1:即(A,C)是可观察的。

标称模型预测控制概述

关于MPC的背景，参见：Rawlings和Mayne[2009]。令表示整数集合，表示正整数集合，且表示从a到b的连续整数的集合{a,…,b}。令表示预测时域，并且u和x表示输入u和状态x的预测值。然后，通过在每个步骤i应用预测的、优化的控制输入轨迹的第一控制输入MPC进行闭环控制，所述优化的控制输入轨迹通过最小化合适的成本函数J(·,·)来表征(为了简洁省略了细节)，

受制于适当的约束，并且进一步受制于使用模型(2)进行的预测：

预测的状态轨迹在(4)中被初始化为判断的模型状态，其值极大地影响所得到的MPC控制律的性能。不进行实际和判断状态之间的符号区分，因为(2)的状态x只能被判断。

控制器定时和输入历史。(2)的采样周期和控制输入u的控制器更新之间的时间间隔被假定为相同且等于T。为了简洁，我们进一步假设使用模型(2)的任何控制器访问精确控制输入历史，其中先前的控制输入u_i应用在恰好T的时间间隔处。通过τ_i＝τ_i-1+T表示控制器调用的实际时间瞬时。

传感器定时、传感器重新校准和输出历史。每个测量由三元组定义，其中表示随着每个新测量增加的测量索引，表示CGM输出，类似于(2b)的y(即，减去设定点y_s)，如在时间瞬时t_j处由CGM提供的。变量表示重新校准计数器，并且在每次重新校准传感器时递增(r_j：＝0)。

连续测量之间的时间间隔可以不是精确的T。然而，我们假设对于所有j，t_j-t_j-1＜2T。类似地，我们假设在τ_i处的控制器调用和在t_i的最近测量之间的时间间隔小于2T。如果间隔超过两个采样周期，则对于低倍数的采样周期的间隔，使用模型(2)的开环预测以“填充间隙”的策略可能是有用的。为了简洁，本文没有考虑这样的场景，尽管它们存在于临床控制器的实施中。

在时间t_i处的每个输出测量由于过程噪声和测量噪声而经受误差。然而，已经证明CGM噪声难以准确地建模(Hovorka[2006])，因此在本文中，我们没有对测量误差做出假设，并且在状态判断方案中没有包括利用噪声特性的感知知识的策略。然而，我们假设测量使得r_j≠r_j-1是精确的，因为r在传感器被重新校准时是递增的。所公开的状态判断策略实现了将高频干扰抑制到一定(可调谐)程度，但是即使没有最近的传感器重新校准，所公开的策略在低频测量偏差为零的假设下判断状态。

基于精确的输出和输入的状态重建。我们用I_a表示a×a单位矩阵，用0_{a,b}表示a×b零矩阵，并且用表示Kronecker乘积。

在每个步骤i，给定与控制器定时τ_i＝τ_i-1+T同步的过去输出(和现在)的精确序列并进一步给定过去控制输入的精确序列可以重建模型(2)的当前状态x_i，如下。令

因此：

x_i＝FX_i (7)

其中，在步骤i，除了X_i之外，所有的是已知的。由(5)和(6)：

然后，通过(5)和(7)表征当前状态x_i。(8)中的倒数由注释1存在，因为

通过输出轨迹拟合的状态判断。在每个步骤i，定义连续时间函数f:的参数θ_i∈Θ被识别，使得其紧密拟合最近的数据点。随后在时间瞬时τ_k，对连续时间函数f(t,θ_i)采样，以合成同步的、过去(和一个现在)输出值的轨迹结合过去控制输入的精确序列使用这种构造的输出轨迹，以通过本所描述的方案构建当前状态x_i的判断。

使用多项式的非约束最小二乘拟合进行函数拟合。可以考虑更一般的成本函数、更一般的函数f(·)以及约束，但是本文省略这些复杂性以集中在定时和传感器重新校准方面的优点。关于CGM数据点的定时和异步性质的益处在于，可以用以任意方式在时间上分布的数据点来进行函数拟合。关于传感器重新校准的重要的、新颖的功能是由于基于优化的性质(与递归判断器相反)，当发生重新校准时可以适应不连续性。不连续的大小无需知道，而是通过优化从数据中识别。假设在最近的历史中，发生至多一次重新校准，则在重新校准之前拟合数据点时包括不连续性，但是当拟合更新的数据点时不包括该不连续性。关键地，当对f(·)采样以合成值的构造的输出轨迹时，不包括不连续性。

优化惩罚从一个步骤到下一步骤的参数的偏差θ_i-θ_i-1，从而引入用于抑制高频干扰的“粘度”。

具有函数不连续性的数据拟合

为了在i继续进行时一致地解释参数θ_i的值，函数f(·)被适配为将当前时间τ_i移动到原点。考虑用于拟合的连续时间函数类别是p阶多项式

其中p是设计参数。令设计参数表示要考虑的测量历史的长度。对于每个步骤i，令表示最近测量的索引，并且令表示传感器重新校准之后的最近测量的索引。为d所指定的范围意味着在M长度历史时域内发生了重新校准。在M长度历史时域之前发生了最新重新校准的情况是简单的，且不进一步讨论。为了简洁，我们不讨论在历史时域M内具有多次重新校准的情况，尽管这种情况可以适应。

在步骤i,用于状态判断的测量是认为r_i＝r_j+1令表示由重新校准导致的测量不连续的(未知)大小，并且定义扩展参数不连续性拟合函数和数据之间的误差表示如下：

令表示惩罚误差e_(i,j)的成本,相对于进行测量的相对时间是时间相关的，但是相对于实际时间不是时间相关的。进一步地，令Q_i≥0表示用于惩罚参数偏差θ_i-θ_i-1的成本。优化扩展参数由以下的二次方程式的解来表征：

通常，应选择成本R_k使得R_k≥R_k+1，即，使得更近的测量比旧的测量更多地影响优化参数估计选择成本矩阵Q_i以惩罚(9)的参数a_(i,k)，并且通常应为对角线。较高的成本允许对例如经由Q_(1,1)的值或经由Q_(2,2)等的速度的变化率设置“粘度”。注意，在重新校准之后，期望选择Q_(1,1)＝0，以便于促进对重新校准步骤改变的瞬时响应。

输出轨迹构造

给定优化的参数通过在时间t∈{0,-T,-2T,…}对函数采样来定义用于通过本文描述的方法构建判断状态的合成输出轨迹。

说明性示例

在本节中，通过简单的数值示例来说明所公开的状态判断策略的行为和益处。参数选择是为了在合理范围内产生最简单的所公开策略的例子。使用(9)的多项式的阶数p＝1，即，我们进行直线拟合。注意，使用的数据点M的数量必须等于或超过函数拟合的自由度。因此，我们选择历史时域M＝3，便于一次重新校准的直线拟合。我们令R₁＝R₂＝1和R₃＝0.1，以惩罚关于最旧的数据点的误差，其小于与最近的两个数据点相关联的误差。最后，我们选择Q＝0_{2,2}，即，优化参数与前一步骤的无关。

我们比较所公开的状态判断器与基于模型(2)的线性状态判断器的响应：

装置模型不匹配的抑制

图1示出了线性状态判断器的增益L如何影响抑制装置模型不匹配的能力。CGM恒定在280mg/dL，并且以基础速率进行胰岛素输注。较高的增益L更有效地抑制不匹配，但导致对噪声响应性的增加。注意，在该示例中，线性状态判断器的状态被初始化以实现稳定状态下的CGM值。尽管这种优化的初始化，线性状态判断器的状态判断漂移，在判断器输出Cx_i和CGM信号中导致稳定状态不匹配。其原因是模型(2)是基于围绕y_s＝110mg/dL的线性化，并且升高的稳态CGM值与基础胰岛素输送不相容。相比之下，公开的状态判断器没有经受这样的不匹配，因为合成的输出轨迹仅基于CGM数据而不是模型(2)来构造，并且因为通过可观察性，此方案构建了与该构造的输出轨迹完全对应的状态。

MPC&CGM同步-采样周期不正确

在这个示例中，我们证明当CGM数据以每9分钟而不是T＝5min传输时(假设控制器同时更新，仅每9分钟发生一次)发生的情形。这不是MPC在实践中如何实现的(本文)；然而，该示例是有启发性的。

我们考虑以1mg/dL/min上升的CGM轨迹，每9min采样一次。CGM数据被递归地输入到判断器(10)，其不能利用数据的时间戳，因为模型(2)是基于T＝5min的采样周期。增益L选择为高，即，判断器是响应性的，并且良好地抑制输出误差。结果如图2所示。尽管实现了输出Cx_i的准确起始值，但是变化率显然被误初始化为高估的值，并且MPC预测偏离CGM轨迹。相比之下，所公开的判断器利用控制器的调用时间和CGM时间戳，并且以适当的方式考虑任意定时。基于所公开的判断器状态，MPC预测是CGM轨迹的延续。

MPC和CGM采样瞬时偏移

在该示例中，我们证明了所公开的判断器适应控制器更新时刻和CGM之间的延迟的能力。我们认为CGM轨迹的变化率为1mg/dL/min，每隔T＝5分钟有数据点。控制器每T＝5分钟更新，关于最新的CGM值延迟4分钟。结果绘制在图3中。尽管有延迟，线性判断器使得MPC预测开始于最近的CGM值。相比之下，所公开的判断器从位于CGM数据轨迹的延续上的外推值启动MPC预测。

当CGM的变化率低(大部分时间是低的)时，所公开的判断器关于延迟补偿的益处是可忽略的。然而，在例如摄取膳食或开始运动之后，CGM信号经历快速变化。正是在这些具有挑战性的时间，控制器的响应性是至关重要的。

MPC和CGM异步

在该示例中，我们考虑控制器按照意图以采样周期T＝5min更新控制输入的情况。CGM值以1mg/dL/min升高，但是仅每7分钟更新其值。由于采样周期中的这种不匹配，MPC和CGM有时同时更新，通常在它们之间存在延迟，并且其他时间自从先前的MPC更新以来没有发生CGM更新。

我们考虑具有高增益的线性状态判断器，在每个控制器调用时用最新的CGM值更新。所得到的MPC预测在图4的顶部子图中示出。预测产生围绕CGM轨迹的羽毛样扩散，其中这种扩散是葡萄糖值偏移以及变化速率的误初始化的结果。相比之下，在图4的底部子图中绘出的是当由所公开的判断器初始化时的MPC预测。预测紧密地重叠。由于控制器的调谐，它们不完全重叠；由于预测的胰岛素输送，预测略微向下偏离。

重新校准

所公开的方法的初始动机是合适地适应传感器重新校准-接下来说明。控制器和CGM同步到正确的采样周期；T＝5min。CGM读数为200mg/dL直到14:25，在14:30重新校准为250mg/dL，并且之后保持在该读数。

使用线性状态判断器的响应在图5中示出。参见估计的血糖水平(灰线)，可以看出，线性判断器在快速收敛方面表现令人满意。线性状态判断器具有高增益，导致判断器状态x的“强制”校正，以产生等于CGM值的输出Cx。然而，这种高增益判断不适于初始化MPC预测，由于在重新校准之后的延长期间的预测的高度动态响应。状态判断中的这种响应导致胰岛素输送中大的、不期望的过冲。低增益线性状态判断器在本文可能更期望用于MPC状态初始化，导致具有较少倾斜的预测，并且因此更保守的胰岛素输送。然而，低增益判断器导致缓慢收敛到正确的葡萄糖水平，并且依赖于葡萄糖值，由于装置模型不匹配而导致偏移。

图6示出了利用所公开的判断器的响应。估计的葡萄糖值在14:30瞬时地改变为重新校准的值，并且状态判断瞬时切换到新的值，其首先反映新的CGM值，并且其次反映在最近的历史中CGM轨迹的变化率。超出重新校准的MPC预测几乎不可见。所得到的胰岛素输送在重新校准时刻经历向上的阶跃变化。来自于稳态输送的两个短期偏差是由于泵的离散化和携带方案。在胰岛素步骤变化之前和之后，由于高血糖，需要超过基础速率的输送。因此，在状态判断器的快速瞬变期间强制基础输送的安全机制将对有效的葡萄糖控制构成障碍。

结论

公开了基于滚动时域优化的新型状态判断方案，以解决与用于基于CGM数据初始化MPC优化的递归状态判断器相关联的问题。使用简单的合成示例证明了所公开的策略的机制和益处。所公开的方法通过帕多瓦大学/弗吉尼亚州FDA公认的代谢模拟器(Kovatchev等人[2009])进行测试，并且在“正常”环境中，即当不处理启发该公开的问题实例时，与响应调谐的线性状态判断器相比较。当模拟更具挑战性的情景时，使用更接近类似于在临床试验中获得的CGM数据的CGM数据来验证所公开的判断器的性能。

所公开的方案为扩展提供了灵活的基础。(a)当远离重新校准时，所公开的方法可以与例如卡尔曼滤波器组合用于处理高频噪声。(b)使用多项式作为拟合函数来描述所公开的方法，但是Miller和Strange[2007]报告傅里叶级数对于拟合到CGM数据是有效的。(c)额外的CGM可以提供比仅仅血糖估计更丰富的数据，例如伴随的置信界限的估计。基于优化的方法提供了利用这种辅助信息的途径。(d)偏倚控制的概念-基于进一步的传感器或用户输入以定义好的方式操纵状态判断的能力-被促进，在检测到例如进餐、锻炼、泵故障或CGM敏感性突然丧失之后提供改进的安全性。

参考文献

Bequette,B.W.,Optimal Estimation Applications to Continuous Gluc ose Monitoring,In Proc.AACC American Control Conf.,958-962页,Bo ston,MA,USA,2004年6月。

Breton,M,Farret,A,Bruttomesso,D,Anderson,S,Magni,L,Pate k,S,Dalla Man,C,Place,J,Demartini,S,Del Favero,S,Toffanin,C,Hughes-Karvetski,C,Dassau,E,Zisser,H,Doyle III,F.J,De Nicolao,G,Avogaro,A,Cobelli,C,Renard,E,&Kovatchev,B.,Fully Integrat ed Artificial Pancreas in Type 1 Diabetes:Modular Closed-Loop Glucose Control Maintains Near Normoglycemia,Diabetes,61(9)：2230-2237,2012年6月。

Cobelli,C,Dalla Man,C,Sparacino,G,Magni,L,De Nicolao,G,&Kovatchev,B.P.,Diabetes:Models,Signals and Control,IEEE Rev.Biomed.Eng.,2:54-96,2009.

Cobelli,C,Renard,E,&Kovatchev,B.,Artificial Pancreas:Past,P resent,Future,Diabetes,60(11):2672-2682,2011年11月。

Doyle III,F.J,Huyett,L.M,Lee,J.B,Zisser,H.C,&Dassau,E.,B ench to Clinic Symposia-Closed Loop Artificial Pancreas Systems:En gineering the Algorithms,Diabetes Care,37:1191-1197,2014年。

Gondhalekar,R,Dassau,E,Zisser,H.C,&Doyle III,F.J.,Periodic-Zone Model Predictive Control for Diurnal Closed-loop Operation of an Artificial Pancreas,J.Diabetes Sci.Technol.,7(6):1446-1460,2013年11月。

Gondhalekar,R,Dassau,E,&Doyle III,F.J.,MPC Design for Rap id Pump-Attenuation and Expedited Hyperglycemia Response to Treat T1DM with an Artificial Pancreas,In Proc.AACC American Control Con f.,Portland,OR,USA,第4224-4230页,2014年6月。

Grosman,B,Dassau,E,Zisser,H.C,Jovanovic,L,&Doyle III,F.J.,Zone Model Predictive Control:A Strategy to Minimize Hyper-and Hypoglycemic Events,J.Diabetes Sci.Technol.,4(4):961-975,2010年7月。

Grosman,B,Dassau,E,Zisser,H,Jovanovic,L,&Doyle III,F.J.,Multi-Zone-MPC:Clinical Inspired Control Algorithm for the Artificial Pancreas,In Proc.18th IFAC World Congress,第7120-7125页,Milan,I taly,2011年8月。

Harvey,R.A,Wang,Y,Grosman,B,Percival,M.W,Bevier,W,Fin an,D.A,Zisser,H,Seborg,D.E,Jovanovic,L,Doyle III,F.J,&Dassau,E.,Quest for the Artificial Pancreas:Combining Technology with Treat ment,IEEE Eng.Med.Biol.Mag.,29(2)：53-62,2010。

Hovorka,R.,Continuous glucose monitoring and closed-loop system s,Diabetic Med.,23(1):1-12,2006年1月。

Hovorka,R,Canonico,V,Chassin,L.J,Haueter,U,Massi-Benedetti,M,Federici,M.O,Pieber,T.R,Schaller,H.C,Schaupp,L,Vering,T,&Wilinska,M.E.,Nonlinear model predictive control of glucose concen tration in subjects with type 1 diabetes.Physiol.Meas.,25:905-920,2004年7月。

Kovatchev,B.P,Breton,M,Dalla Man,C,&Cobelli,C.,In Silico Preclinical Trials:A Proof of Concept in Closed-Loop Control of Type1 Diabetes,J.Diabetes Sci.Technol.,3(1):44-55,2009年1月。

Kuure-Kinsey,M,Palerm,C.C,&Bequette,B.W.,A Dual-Rate Kal man Filter for Continuous Glucose Monitoring,In Proc.EMBS Annual I nt.Conf.,pages 63-66,New York City,NY,USA,2006年8月。

Levine,W.S,editor.,The Control Handbook,CRC Press,Boca Rato n,FL,USA,第2版,2011。

Magni,L,Raimondo,D.M,Dalla Man,C,De Nicolao,G,Kovatch ev,B,&Cobelli,C.,Model predictive control of glucose concentration in type 1diabetic patients:An in silico trial,Biomed.Signal Process.C ontrol,4(4):338-346,2009。

Magni,L,Raimondo,D.M,Bossi,L,Dalla Man,C,De Nicolao,G,Kovatchev,B,&Cobelli,C.,Model Predictive Control of Type 1 Diab etes:An in Silico Trial,J.Diabetes Sci.Technol.,1(6):804-812,2007年11月。

Miller,M&Strange,P.,Use of Fourier Models for Analysis and I nterpretation of Continuous Glucose Monitoring Glucose Profiles,J.Diab etes Sci.Technol.,1(5)：630-638,2007年9月。

Parker,R.S,Doyle III,F.J,&Peppas,N.A.,A Model-Based Algorit hm for Blood Glucose Control in Type I Diabetic Patients,IEEE Trans.Biomed.Eng.,46(2)：148-157,1999年2月。

Rawlings,J.B&Mayne,D.Q.,Model Predictive Control:Theory an d Design,Nob Hill Publishing,Madison,WI,USA,2009年8月。

Turksoy,K,Bayrak,E.S,Quinn,L,Littlejohn,E,&Cinar,A.,Mul tivariable Adaptive Closed-Loop Control of an Artificial Pancreas Witho ut Meal and Activity Announcement,Diabetes Technol.Ther.,15(5)：386-400,2013年5月。

van Heusden,K,Dassau,E,Zisser,H.C,Seborg,D.E,&Doyle III,F.J.,Control-Relevant Models for Glucose Control Using A Priori,Pati ent Characteristics,IEEE Trans.Biomed.Eng.,59(7):1839-1849,2012年7月。

Walsh,J&Roberts,R.,Pumping Insulin,Torrey Pines Press,San Diego,CA,USA,第4版,2006。

Zisser,H.,Clinical Hurdles and Possible Solutions in the Implement ation of Closed-Loop Control in Type 1 Diabetes Mellitus,J.Diabetes Sci.Technol.,5(5)：1283-1286,2011年9月。