检测动脉血管粘弹性的系统及方法与流程

本发明涉及一种检测动脉血管粘弹性的系统及方法，尤其涉及一种在体定量检测动脉血管粘弹性的系统及方法。

背景技术：

心脑血管疾病是心脏血管和脑血管疾病的统称，泛指由于高脂血症、血液黏稠、动脉粥样硬化、高血压等所导致的心脏、大脑及全身组织发生的缺血性或出血性疾病。众所周知，心血管疾病是人类头号的杀手，全球每年死于心脑血管疾病的人群高达1500万人，我国心脑血管病患高达2.9亿，年住院总费用超过700亿元，心血管病的疾病负担日渐加重，已成为我国重大的公共卫生问题。

动脉的力学特性在心血管功能中起核心作用，动脉僵硬度和各种心血管疾病之间有直接的关系，是心脑血管发病率和死亡率重要的预测因子。虽然动脉血管的粘弹性的变换一般是全身性的，并影响整个血管系统，但是不同位置的动脉血管的硬度对年龄增大、高血压、妊娠等因素的反应也不一样，往往动脉血管变硬，而主动脉血管变软，所以精确测量局部动脉显得十分重要。由于动脉血管壁的粘弹性随着血压的变化成非线性变化，这种非线性变化对整个心血管系统的健康运作至关重要，并且还可以检测出动脉粥样硬化中不稳定的板块。

为了获得局部的、瞬时、定量的硬度测量，不能依靠心脏泵血对血管产生的压缩波，因为心脏一秒大约产生一次波动，利用超声基于声辐射力的剪切波弹性成像可以满足一次心动周期下对血管壁进行多次瞬时测量，但是该方法有一定的局限性：第一，声辐射力用于血管检测的安全性有待考证；第二，此方法必须借助该团队拥有自主产权的快速剪切波成像设备才能实现，系统复杂，造价昂贵，不便于推广。

技术实现要素：

有鉴于此，有必要提供一种安全性更高的在体定量检测动脉血管粘弹性的系统及方法。

一种检测动脉血管粘弹性的系统，该系统包括主控机、与所述主控机电性连接的发射/接收模块及心电采集模块，与所述发射/接收模块分别电性连接的外部振子及超声探头，与所述心电采集模块分别电性连接的心电采集机，所述主控机包括处理模块、估计模块及配准模块，其中：所述发射/接收模块用于在心动周期下控制外部振子在靠近血管的皮肤上产生振动；所述发射/接收模块还用于在心动周期下驱动超声探头向皮肤发射检测脉冲，记录超声探头每个通道下的皮肤内血管组织的脉冲回波信号；所述处理模块用于根据上述记录的每个通道下的皮肤内血管组织的脉冲回波信号，计算得到每个通道的皮肤内血管组织的位移，并滤除所述位移中的脉搏波速度；所述心电采集模块用于在心动周期下触发心电采集机采集心电信号；所述估计模块用于根据上述得到的滤除脉搏波速度后每个通道的皮肤内血管组织的位移，求得应变波的瞬时传播速度，估计血管的瞬时粘弹性系数；所述配准模块用于将估计的血管的瞬时粘弹性系数与采集的心电信号在时间上配准，得到心动周期下不同时刻血管的弹性模量、粘性模量。

其中，所述超声探头为多通道超声探头。

所述的处理模块用于计算得到每个通道的皮肤内血管组织的位移，具体为：从检测振元接收到的射频信号经过超声前端电路的放大和模数转换的处理，再经过正交解调处理，得到射频信号的复包络；对某一检测点，对回波信号相邻帧的复包络信号进行互相关处理，提取出该点不同深度中组织振动的信号；计算所述检测点在某个深度上振动信号的相位，每一帧的相位减去相邻帧的相位，获得各帧的相位差，进而得到血管组织的随时间变化的位移曲线，对于相距z的两个检测点，可以通过两个检测点的某一深度的位移曲线求取相速度cl。

所述的估计模块基于兰姆波数学模型f(c,ω,μ1,μ2)＝0，具体包括：

i.假定<μ1,μ2>的一组初值；

ii.基于“最小二乘准则”得到相速度谱的估计即：

iii.计算估计的相速度谱与实测相速度谱cphase(ω)之间的误差平方和，表示为：

iv.若α(μ1,μ2)未达到预设的精度，更新的值，返回第ii步；

否则计算停止，所得是血管的瞬时粘弹性系数的估计值。

所述的配准模块具体用于：将估计的血管的瞬时粘弹性系数与采集的心电信号在时间上做配准，以得到心动周期下不同时刻的血管弹性模量和粘性模量。

本发明还提供一种检测动脉血管粘弹性的方法，该方法包括如下步骤：a.控制外部振子在靠近血管的皮肤上产生振动；b.多通道的超声探头向皮肤发射检测脉冲，记录每个通道下皮肤内血管组织的脉冲回波信号，并计算得到每个通道的皮肤内血管组织的位移，并滤除所述位移中的脉搏波速度，同时心电采集机开始采集心电信号；c.根据上述得到的滤除脉搏波速度后每个通道的皮肤内血管组织的位移，求得应变波的瞬时传播速度，估计血管的瞬时粘弹性系数；d.将估计的血管的瞬时粘弹性系数与采集的心电信号在时间上配准，得到心动周期下不同时刻血管的弹性模量和粘性模量。

其中，所述的步骤b包括：从检测振元接收到的射频信号经过超声前端电路的放大和模数转换的处理，再经过正交解调处理，得到射频信号的复包络；对某一检测点，对回波信号相邻帧的复包络信号进行互相关处理，提取出该点不同深度中组织振动的信号；计算所述检测点在某个深度上振动信号的相位，每一帧的相位减去相邻帧的相位，获得各帧的相位差，进而得到血管组织的随时间变化的位移曲线，对于相距z的两个检测点，可以通过两个检测点的某一深度的位移曲线求取相速度cl。

该方法还包括：在一个心动周期内，重复执行步骤a至步骤c。

所述的步骤c具体流程如下：

i.假定<μ1,μ2>的一组初值；

ii.基于“最小二乘准则”得到相速度谱的估计即：

iii.计算估计的相速度谱与实测相速度谱cphase(ω)之间的误差平方和，表示为：

iv.若α(μ1,μ2)未达到预设的精度，更新的值，返回第ii步；

否则计算停止，所得是血管的瞬时粘弹性系数的估计值。

所述的步骤d具体包括：将估计的血管的瞬时粘弹性系数与采集的心电信号在时间上做配准，以得到一个心动周期内不同时刻的血管弹性模量和粘性模量。

本发明检测动脉血管粘弹性的系统及方法，利用外部振子与超声相结合的方式在体定量检测动脉血管粘弹性，优点如下：(1)本发明采用外部振子代替超声探头，在体定量测量具有更高的安全性；(2)本发明既可以形成一个独立的设备，简单便携，也可以作为一个附加功能模块，加载在现有的彩超系统上使用，节约成本，便于推广。

附图说明

图1为本发明检测动脉血管粘弹性的系统的硬件架构图；

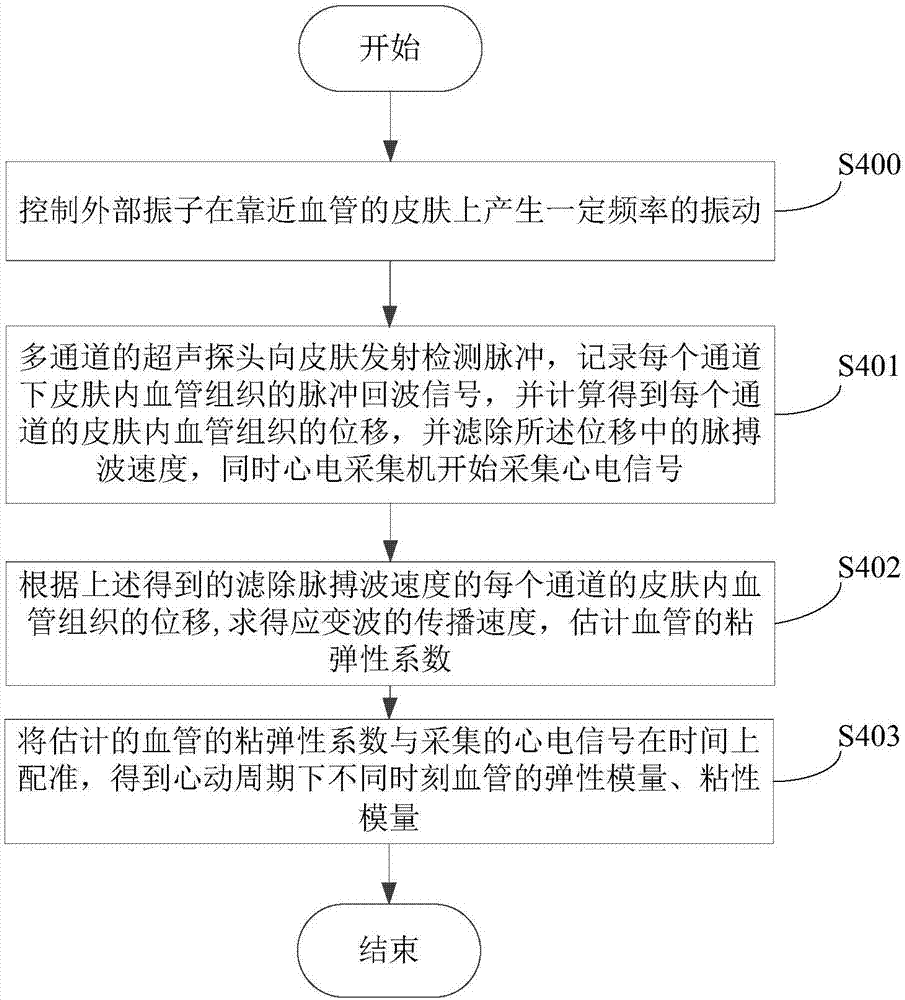
图2为本发明检测动脉血管粘弹性的方法的流程图。

具体实施方式

首先对本发明的物理基础进行如下介绍：

本发明使用外部振子(20hz-1000hz)充当振动源的激励方法，即将低频振动器置于体表，或者将振动器和超声探头集成在一起，以便操作。通过振动源向体内传播低频振动，用超声探头检测振动引起的剪切波在血管组织中传播时的速度信息。作用力施加于人体的体表，以激励皮下的血管组织，直接模拟了医生用手指以一定的频率按压人体组织实施检查的过程，更为直观简单并且安全性更高，由于血管是一种薄层管状结构的组织，剪切波在其内传播时，不断地角膜的上下边界发生作用，产生折射、反射及横波与纵波之间的模态转换而形成兰姆波。

对于浸在液体中的粘弹性薄板，假设薄板和液体的密度相近且它们中的可压缩波波数远小于兰姆波波数，则薄板中的非对称兰姆波弥散方程如下：

其中，kl＝ω/cl,ω是角频率，cl是频率相关的兰姆波相速度，是剪切波的波数，μ是剪切模量，ρm是样品的密度(与水的密度相近)，h等于样品厚度的一半。

通过引入voigt模型来描述粘弹性薄板的力学行为，剪切模量μ则表示为μ＝μ1+iωμ2，其中μ1和μ2分别是弹性模量和粘性模量。因此，方程(1)可化为关于兰姆波相速度cl、频率ω、弹性模量μ1和粘性模量μ2的数学模型，如下所示。

此式表明，兰姆波速度是弹性、粘性以及兰姆波频率的函数。通过测量兰姆波并在频域上分解得到各频率上的兰姆波速度cl(ω)，由非线性拟合即可估计出样品的弹性模量μ1和粘性模量μ2，这是本发明的物理基础。具体实现中，对角膜粘弹性的估计以方程(2)作为数学模型，或者对方程(2)进行一定的近似和简化，得到血管粘弹性估计的经验公式(须经过实验的验证)，作为估计的数学模型。

理论分析和实验研究表明，血管内的兰姆波的速度一般在3～10m/s，在医用超声上，这样的传播速度完全可以用既有的硬件检测到。

下面结合附图及具体实施例对本发明作进一步详细的说明。

参阅图1所示，是本发明检测动脉血管粘弹性的系统的硬件架构图。

该系统包括主控机101、发射/接收模块102、心电采集模块103、外部振子104、超声探头105及心电采集机106。其中：发射/接收模块102分别与主控机101、外部振子104、超声探头105电性连接；心电采集模块103分别与主控机101、心电采集机106电性连接。

所述主控机101控制整个系统的运作，负责整个系统的信号控制及数据处理。所述主控机101包括处理模块107、估计模块108及配准模块109。

所述发射/接收模块102包括发射电路及接收电路，发射电路包括信号发生器及功率放大器。所述心电采集模块103用于触发心电采集机106。所述外部振子104用于在皮肤表面产生振动。所述超声探头105包括多个通道，即多个检测振元，也称检测点，在本实施例中所述超声探头105包括2个通道，即通道a和通道b，所述通道之间具有微小间距。

所述发射/接收模块102用于控制外部振子104在靠近血管的皮肤上产生一定频率的振动。具体而言：

本实施例中首先将外部振子104放在靠血管的皮肤上，通过主控机101触发发射/接收模块102的发射控制，控制发射电路使外部振子104每0.1秒钟产生1次频率的振动，导致血管有一个微小的振动，所述振动以兰姆波的形式在血管中传播。

所述发射/接收模块102还用于驱动超声探头105向皮肤发射检测脉冲，记录每个通道下的皮肤内血管组织的脉冲回波信号。

所述处理模块107用于根据所述发射/接收模块102记录的每个通道下的皮肤内血管组织的脉冲回波信号，计算得到每个通道的皮肤内血管组织的位移，并滤除所述位移中的脉搏波速度。具体而言：

将接收到的所述检测脉冲的回波信号r(t,k)表示为一个二维信号。发射一次检测脉冲，则不同时刻t的回波信号表示组织中不同深度处的回波。在本实施例中，通道a、b以一定的脉冲重复频率发射检测脉冲，探测血管组织的位移，得到所述位移对时间的曲线，其原理与脉冲多普勒的原理相类似。

进一步地，按一定的脉冲重复频率发射多次检测脉冲，得到一个检测脉冲的回波序列，k表示该序列中回波的帧数。回波信号的幅度和相位受到该点组织振动的调制，通过一定的算法可从中提取出血管组织振动的相位变化。在具体实现时，从检测振元接收到的射频(rf)信号经过超声前端电路的放大和模数转换的处理，再经过正交解调处理，得到rf信号的复包络。对某一检测点，回波信号相邻帧的复包络信号进行互相关处理，提取出该点不同深度中组织振动的信号。

计算所述检测点在某个深度上振动信号的相位，每一帧的相位减去相邻帧的相位，获得各帧的相位差，进而得到血管组织的随时间变化的位移曲线。对于相距z的两个检测点，可以通过两个检测点的某一深度的位移曲线求取相速度cl。

所述心电采集模块103用于触发心电采集机106采集心电信号。

所述估计模块108用于根据上述得到的滤除脉搏波速度后每个通道的皮肤内血管组织的位移，求得应变波的瞬时传播的相速度，估计血管的瞬时粘弹性系数。

在本实施例中，根据上述得到通道a、b下的皮肤内血管组织的位移对时间的曲线可以计算出振动在两点传播的相速度，通过数学模型估计血管的粘弹性系数。

本实施例基于数学模型f(c,ω,μ1,μ2)＝0对弹性系数μ1和粘性系数μ2进行估计是典型的基于模型的非线性参数估计问题，采用非线性最小二乘估计方法解决。下面简单描述具体的流程：

i.假定<μ1,μ2>的一组初值；

ii.基于“最小二乘准则”得到相速度谱的估计即：

iii.计算估计的相速度谱与实测相速度谱cphase(ω)之间的误差平方和，表示为：

iv.若α(μ1,μ2)未达到预设的精度，更新的值，返回第ii步；

否则计算停止，所得是血管的瞬时粘弹性系数的估计值。

具体实现中可采用迭代法或搜索法等优化算法得到<μ1,μ2>的最优估计。

所述配准模块109用于将估计的血管的瞬时粘弹性系数与采集的心电信号在时间上配准，得到心动周期下不同时刻血管的弹性模量、粘性模量。具体而言：

本实施例中，在大约一秒的心动周期下，重复上述的方式激励血管振动并采集回波信号多次，与采集的心电信号在时间上做配准，从而得到心动周期下的不同时刻的血管弹性模量和粘性模量。

参阅图2所示，是本发明检测动脉血管粘弹性的方法较佳实施例的作业流程图。

步骤s400，控制外部振子104在靠近血管的皮肤上产生一定频率的振动。具体而言，主控机101通过发射/接收模块102控制外部振子104产生一定频率的振动，作用于外部振子104下面的血管组织使其产生振动，并向周围横向传播。

步骤s401，多通道的超声探头105向皮肤发射检测脉冲，记录每个通道下皮肤内血管组织的脉冲回波信号，计算得到每个通道的皮肤内血管组织的位移，并滤除所述位移中的脉搏波速度，同时心电采集机106开始采集心电信号。具体而言：

将接收到的所述检测脉冲的回波信号r(t,k)表示为一个二维信号。发射一次检测脉冲，则不同时刻t的回波信号表示组织中不同深度处的回波。在本实施例中，通道a、b以一定的脉冲重复频率发射检测脉冲，探测血管组织的位移，得到所述位移对时间的曲线，其原理与脉冲多普勒的原理相类似。

进一步地，按一定的脉冲重复频率发射多次检测脉冲，得到一个检测脉冲的回波序列，k表示该序列中回波的帧数。回波信号的幅度和相位受到该点组织振动的调制，通过一定的算法可从中提取出血管组织振动的相位变化。在具体实现时，从检测振元接收到的射频(rf)信号经过超声前端电路的放大和模数转换的处理，再经过正交解调处理，得到rf信号的复包络。对某一检测点，回波信号相邻帧的复包络信号进行互相关处理，提取出该点不同深度中组织振动的信号。

计算所述检测点在某个深度上振动信号的相位，每一帧的相位减去相邻帧的相位，获得各帧的相位差，进而得到血管组织的随时间变化的位移曲线。对于相距z的两个检测点，可以通过两个检测点的某一深度的位移曲线求取相速度cl。

步骤s402，根据上述得到的滤除脉搏波速度后每个通道的皮肤内血管组织的位移，求得应变波的瞬时传播的相速度，估计血管的瞬时粘弹性系数。

在本实施例中，根据上述得到通道a、b下的皮肤内血管组织的位移对时间的曲线可以计算出振动在两点传播的相速度，通过数学模型估计血管的粘弹性系数。

本实施例基于数学模型f(c,ω,μ1,μ2)＝0对弹性系数μ1和粘性系数μ2进行估计是典型的基于模型的非线性参数估计问题，采用非线性最小二乘估计算法解决。下面简单描述具体的流程：

i.假定<μ1,μ2>的一组初值；

ii.基于“最小二乘准则”得到相速度谱的估计即：

iii.计算估计的相速度谱与实测相速度谱cphase(ω)之间的误差平方和，表示为：

iv.若α(μ1,μ2)未达到预设的精度，更新的值，返回第ii步；

否则计算停止，所得是血管的瞬时粘弹性系数的估计值。

具体实现中可采用迭代法或搜索法等优化算法得到<μ1,μ2>的最优估计。

步骤s403，将估计的血管的瞬时粘弹性系数与采集的心电信号在时间上配准，得到心动周期下不同时刻血管的弹性模量、粘性模量。具体而言：

本实施例中，在大约一秒的心动周期下，重复上述的方式激励血管振动并采集回波信号多次，与采集的心电信号在时间上做配准，从而得到心动周期下的不同时刻的血管弹性模量和粘性模量。

本发明在心动周期下多次测量。因为在脉动的血管中，血压在变化，血压不同粘弹性也会不同，比如像橡皮筋一样，拉紧与放松状态下的硬度和弹性会不一样。因此，本实施例在大约一秒的心动周期下进行多次(≥10)测量，可以得到心动周期下不同时刻下的瞬时粘弹性谱，对诊断人体血管病变具有重要意义。本实施例中外部阵子激励的脉冲重复频率为10hz，即每0.1秒振动一次，每次振动都会发射一定量的检测脉冲检测位移随时间变化，获得血管的粘弹性系数。

本发明检测动脉血管粘弹性的系统，可以为独立的装置，也可以作为附加的功能模块，加载在普通彩超系统上。在作为附加的功能模块时，只需要在普通彩超系统上加载外部振子104、及心电采集机106即可实现，节约成本，方便简单。

虽然本发明参照当前的较佳实施方式进行了描述，但本领域的技术人员应能理解，上述较佳实施方式仅用来说明本发明，并非用来限定本发明的保护范围，任何在本发明的精神和原则范围之内，所做的任何修饰、等效替换、改进等，均应包含在本发明的权利保护范围之内。