一种用于生物光声内窥成像的光吸收系数重建方法与流程

本发明涉及一种利用生物腔体组织产生的光声信号重建组织光吸收系数空间分布的方法，属于医学成像技术领域。

背景技术：

光声层析成像是一种新型的非电离式生物医学功能成像方法，它结合了超声成像的高分辨率和光学成像的高对比度的优势。pat成像方法的逆问题包括声学和光学两方面：声学逆问题是指根据超声探测器采集到的光声信号(本质是超声波)重建组织内部的初始声压分布或空间光吸收能量密度；光学逆问题是指根据超声探测器采集到的光声信号或者据此重建出的光吸收能量密度，估算组织光学特性参数的空间分布，得到对组织光学特性的定量评价。光吸收能量密度是由局部的光吸收系数和光子数分布共同决定的，并不能反映组织的光学特性，而光吸收系数与组织的化学成分密切相关，正常和病变组织的光学特性参数之间通常有较明显的差异，因此组织光吸收系数的空间分布图可为疾病的早期诊断提供更加准确可靠的基础参考信息。但到目前为止，组织光吸收系数的重建方法仍不成熟，还有必要进一步进行研究。

技术实现要素：

本发明的目的在于针对现有技术之弊端，提供一种用于生物光声内窥成像的光吸收系数重建方法，以获取不同组织的光吸收系数之间的差异，为疾病的早期诊断提供机体组织变化的准确可靠的参考信息。

本发明所述问题是以下述技术方案解决的：

一种用于生物光声内窥成像的光吸收系数重建方法，所述方法首先根据超声探测器从各个角度采集的生物腔体组织产生的光声信号重建出光吸收能量分布的测量值；然后通过前向仿真获得光吸收能量分布的理论值；最后根据光吸收能量分布的测量值和理论值构造目标函数，并通过对目标函数进行优化，重建出腔体横截面上组织光吸收系数的空间分布。

上述用于生物光声内窥成像的光吸收系数重建方法，所述重建按以下步骤进行：

a.重建光吸收能量分布的测量值

在直线扫描模式下，根据超声探测器从各个测量角度采集到的周围组织产生的光声信号，得到光吸收能量分布的测量值：

其中，r是θ-l平面极坐标系中的一点，c是光在组织内的传播速度，hm(r)是位置r处的光吸收能量分布的测量值，z0是位置r处与组织表面θ轴之间的垂直距离，ri是与角度θi(i＝1,2,...,m)相对应的位置，cs是超声信号在组织中传播速度，β是组织的等压膨胀系数，cp是组织的比热容，pi(r,t)是超声探测器在时刻t、角度θi(i＝1,2,...,m)、位置r处采集到的组织产生的光声信号的声压；

b.通过前向仿真获得光吸收能量分布的理论值

首先，用由节点表示的面积元对成像区域进行离散化，并根据成像区域内每个节点处光扩散方程的差分形式，计算出位置r处的光子密度函数φ(r)；

然后根据位置r处的光子密度函数φ(r)得到光吸收能量密度的理论值h(r,μa(r))：

h(r,μa(r))＝μa(r)·h·f·φ(r)

其中，μa(r)是位置r处组织的光吸收系数，h是普朗克常数，f是入射光的频率；

c.重建光吸收系数的空间分布

假定组织的光散射系数已知，利用下式求得光吸收系数的空间分布：

其中，c是与光声信号采集系统有关的标定因子，是估算出的、待测区域内位置r处的光吸收系数。

本发明能够利用生物腔体组织产生的光声信号完整地重建出腔体横截面上组织光吸收系数的空间分布，为疾病的早期诊断提供机体组织变化的准确可靠的参考信息。

附图说明

下面结合附图对本发明作进一步说明。

图1是含有脂质斑块的血管横截面示意图；

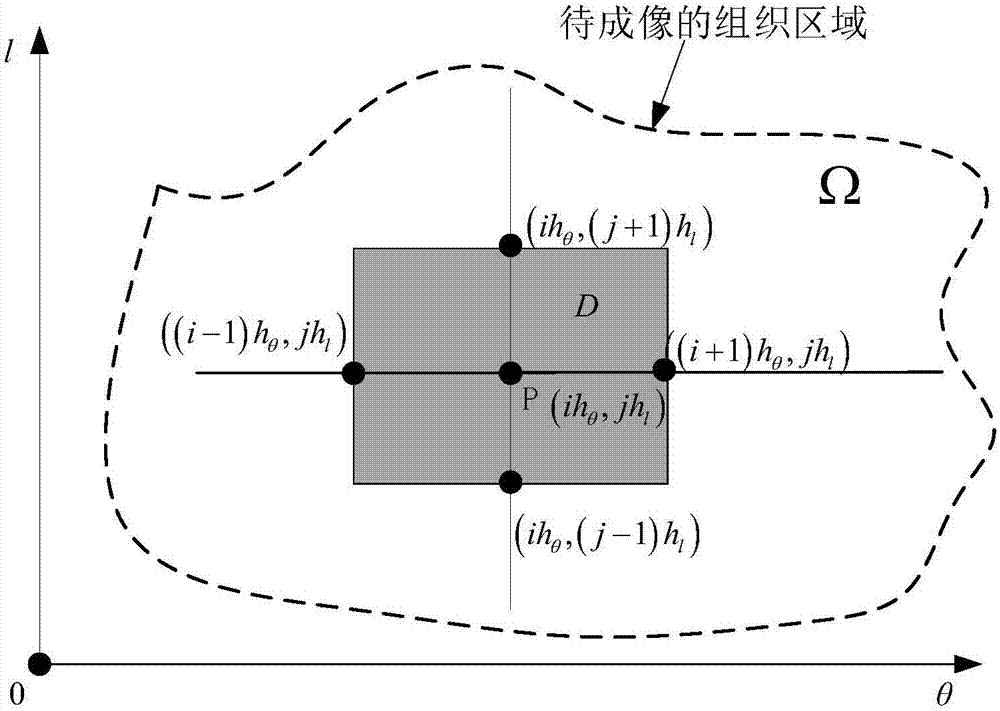
图2是θ-l极坐标平面内网格划分的内点示意图；

图3是θ-l极坐标平面内网格划分的边界点示意图；

图4是腔体成像区域内面向光源的边界点示意图。

文中各符号为：θ、极角；l、极径；θ-l、平面极坐标系；m、血管横截面被等角度分割的总份数；θi、成像导管的第i个测量角度，其中i＝1,2,...,m；r、θ-l平面极坐标系中的一点；hm(r)、位置r处的光吸收能量分布的测量值；z0、位置r处与组织表面θ轴之间的垂直距离；ri、θ-l平面中与角度θi(i＝1,2,...,m)相对应的位置；cs、超声信号在生物软组织中的传播速度；β、组织的等压膨胀系数；cp、组织的比热容；pi(r,t)、超声探测器在时刻t、角度θi、位置r处采集到的组织产生的光声信号的声压，其中i＝1,2,...,m；哈密顿算子；φ(r)、位置r处的光子密度函数；φ(r,rs,q)、时刻t位置r处的时域光子密度函数的laplace变换；δ(r-rs)、位置r处无向点源的laplace变换；q、laplace变换的复频率因子，当q＝0时，de是稳态扩散方程；ω、待成像的组织区域；c、光在组织内的传播速度；组织表面点处的外法向量；qs、光源强度；rs、θ-l平面极坐标系中光源所在位置；rf、扩散传输内反射系数；n、组织相对于环境的相对折射率；μa(r)、位置r处组织的光吸收系数；μs(r)、位置r处组织的光散射系数；μ′s(r)、位置r处组织的约化散射系数；g、组织的各向异性因子；d、ω中一个充分光滑的区域；hθ、沿θ轴的正向步长；hl、沿l轴的正向步长；p、区域d中的一点；(ihθ,jhl)、网格划分后θ-l坐标系中点p的坐标；φi,j、节点(ihθ,jhl)处的光子密度函数值；ki+1,j、点((i+1)hθ,jhl)处的k值；ki,j+1、点(ihθ,(j+1)hl)处的k值；ki-1,j、点((i-1)hθ,jhl)处的k值；ki,j-1、点(ihθ,(j-1)hl)处的k值；|ab|、线段ab的长度；|be|、线段be的长度；|ea|、线段ea的长度；|d|、区域d的面积；h(r,μa(r))、位置r处光吸收能量密度的理论值；h、普朗克常数；f、入射光的频率；c、与光声信号采集系统有关的标定因子；待测区域内位置r处估算出的光吸收系数；x、待求的μa(r)；f(x)、待优化的目标函数；位置r处光吸收系数的估计值；λ、正则化参数；x0、p0、光吸收系数和次梯度的初始值；xn+1、pn+1、n次迭代后的光吸收系数和次梯度；xn、pn、n-1次迭代后的光吸收系数和次梯度；<pn,x>、pn与x的内积；m、ne×n维的稀疏矩阵；ne、迭代次数；n、网格个数；|·|、l1准则；α、惩罚参数；ν、第n次迭代产生的残余量，其初始值v0＝0；shrink(·)、shrink算子；wn、第n次搜索的方向；b0、近似逆hessian矩阵的初始值；i、单位矩阵；bn、第n次迭代的近似逆hessian矩阵；an、步长；g(x)在xn的梯度。

具体实施方式

本发明的处理步骤包括：

1.由超声探测器接收到的光声信号重建光吸收能量分布的测量值

如附图1所示，以血管内光声成像为例，成像导管(超声探测器位于成像导管顶端，用于接收周围组织产生的光声信号)位于血管横截面的中心，周围由内向外依次为管腔、粥样硬化斑块、血管壁内膜/中膜和外膜。忽略超声探测器的孔径效应，将其看作理想的点换能器，其扫描轨迹为平行于成像平面的圆形轨迹。

血管横截面所在的坐标系是θ-l极坐标系，其中θ是极角，l是极径，坐标原点是成像导管中心，水平向右的方向为θ轴正方向。以坐标原点为中心，将血管横截面等角度分成m个扇区，成像导管的第i个测量角度是θi＝360(i-1)/m，其中i＝1,2,...,m。

在直线扫描模式下，根据超声探测器采集到的光声信号，得到光吸收能量分布的测量值：

其中，r是θ-l平面极坐标系中的一点，c是光在组织内的传播速度，hm(r)是位置r处的光吸收能量分布的测量值，z0是位置r处与组织表面θ轴之间的垂直距离，ri是与角度θi(i＝1,2,...,m)相对应的位置，cs是超声信号在生物软组织中的传播速度，β是组织的等压膨胀系数，cp是组织的比热容，pi(r,t)是超声探测器在时刻t、角度θi(i＝1,2,...,m)、位置r处采集到的组织产生的光声信号的声压。

2.通过前向仿真获得光吸收能量分布的理论值

首先，用由节点表示的面积元对成像区域进行离散化，并根据成像区域内每个节点处光扩散方程的差分形式，计算出位置r处的光子密度函数φ(r)。具体步骤如下：

采用准直光源模型，将光源视为组织边界处的内向光子流，进而嵌入到robin边界条件中，则边界含有光源项的de复频域表达式为：

其中，是哈密顿算子；r是θ-l坐标系中的一点；φ(r,rs,q)是时刻t位置r处的时域光子密度函数的laplace变换；δ(r-rs)是位置r处无向点源的laplace变换；q是laplace变换的复频率因子，当q＝0时，de是稳态扩散方程；ω是待成像的组织区域；c是光在组织内的传播速度；是组织表面点处的外法向量；qs是光源强度；rs是θ-l平面极坐标系中光源所在位置；rf是扩散传输内反射系数：

rf≈-1.4399n^-2+0.7099n^-1+0.6681+0.0636n(3)

式(3)中，n是组织相对于环境的相对折射率；μa(r)和μs(r)分别是位置r处组织的光吸收系数和散射系数；当μs'＞＞μa时

其中，μs′(r)是位置r处组织的约化散射系数：

μ′s(r)＝μs(r)(1-g)(5)

其中g是组织的各向异性因子。

在ω中取一个充分光滑的区域d∈ω，在θ-l平面内，对区域d进行矩形网格划分，沿θ轴和l轴的正向步长分别为hθ和hl，d中的一点p在θ-l坐标系中的坐标是(ihθ,jhl)，在区域d上，对式(2)进行积分，得到：

如附图2所示，阴影部分为区域d，若p是内点，则式(6)的差分形式为：

其中，φi,j是节点(ihθ,jhl)处的光子密度函数值；根据式(4)求出ki,j，其中，ki+1,j是在点((i+1)hθ,jhl)处的k值，ki,j+1是在点(ihθ,(j+1)hl)处的k值，ki-1,j是在点((i-1)hθ,jhl)处的k值，ki,j-1是在点(ihθ,(j-1)hl)处的k值。

如附图3所示，由弧线线段ab和be组成区域d，若p是边界点，则式(6)的差分形式为：

式中，|ab|、|be|和|ea|分别是线段ab、be和ea的长度；|d|是区域d的面积。

如附图4所示，光源沿l轴即径向入射，由弧线线段ab和be组成区域d，若p是面向光源的边界点，则式(6)的差分形式为：

然后，根据位置r处的光子密度函数φ(r)得到光吸收能量密度的理论值h(r,μa(r))：

h(r,μa(r))＝μa(r)·h·f·φ(r)(10)

其中，h是普朗克常数，f是入射光的频率。

3.重建光吸收系数的空间分布

假定组织的光散射系数已知，求解光吸收系数分布的问题表述为如下的非线性最小二乘问题：

其中，c是与光声信号采集系统有关的标定因子，是估算出的、待测区域内位置r处的光吸收系数。为表述方便，用x表示μa(r)，并定义：

f(x)＝||hm(r)-c·h(r,x)||²(12)

该最优化问题是一个病态问题，本发明方法采用tv正则化(gaoh,zhaoh.multilevelbioluminescencetomographybasedonradiativetransferequationpart1:l1regularization.opticsexpress,2010,18(3):1854-1871.)使其良态化，将待优化的目标函数改写为：

其中，是位置r处光吸收系数的估计值；λ是正则化参数，在迭代过程中设定λ＝1。

本发明采用bregman方法(gaoh,zhaoh,oshers.bregmanmethodsinquantitativephotoacoustictomography.camreport,2010,30(6):3043-3054)迭代求解式(13)的最优解。具体步骤如下：

设定各参数的初始值：光吸收系数x0＝0，次梯度p0＝0。第n次迭代后，光吸收系数xn+1与次梯度pn+1的结果为：

其中，<pn,x>是次梯度pn与x的内积。

在离散网格条件下，式(14)右端的tv项简化为

||x||tv＝|mx|(16)

其中，m是ne×n维的稀疏矩阵，ne是迭代次数，n是网格个数，|·|是l1准则。

令

dn＝mxn(17)

将式(14)转化为无约束问题：

其中，α是惩罚参数，取值为1。对式(18)进行n次迭代后的结果为：

νn+1＝νn+dn+1-mxn+1(21)

其中，vn+1是第n次迭代产生的残余量，其初始值ν0＝0；shrink算子的定义为：

设

求解xn+1＝argmin[g(x)]最小化问题的具体步骤如下：

步骤1：初始化，设x0＝0，近似逆hessian矩阵的初始值b0＝i；

步骤2：计算搜索方向：其中bn是第n次迭代的近似逆hessian矩阵；

步骤3：沿搜索方向找到下一个迭代点：

其中，an是步长；是g(x)在xn的梯度：

的更新方法是：

步骤4：根据判断迭代是否停止；

步骤5：更新搜索方向wn。