一种基于干扰观测器的主动型膝上假肢终端滑模控制方法与流程

本发明涉及主动型膝上假肢领域，是一种基于干扰观测器的主动型膝上假肢终端滑模控制方法。

背景技术：

众所周知，我国是世界上人口最多的国家，在如此庞大的人口基数下，残疾人的数量也十分巨大。我国政府曾先后于1987年和2006年进行了两次全国残疾人抽样调查，结果显示，肢体残疾者由1987年的755万人猛增至2006年的2412万人。而在2010年，中国残疾人联合根据第六次全国人口普查及第二次全国残疾人抽样调查结果，推算出2010年末我国肢体残疾将达到2472万人，而且随着近年来人口老龄化加剧，交通事故和自然灾害频发，这一数字仍在逐年增加。就目前的医疗水平而言，还没有任何技术手段可以让失去的肢体再生，因此，对于这些肢体残疾者而言，穿戴假肢是他们恢复运动能力的重要途径。随着科技的不断发展和人民生活水平的提高，传统的被动型假肢已经无法满足残疾人的需要，因此主动型下肢假肢已经成为康复领域的研究热点。

主动型膝上假肢的作用是代替截肢者失去的肢体，帮助穿戴者完成一系列动作，使穿戴者能够克服截肢所带来的生活上和工作上的障碍。控制主动型膝上假肢运动的最终目的是使穿戴者的行走步态达到与正常人一致的水平。目前应用于下肢假肢的控制方法中主要有专家控制和神经网络控制。申请号201110456535.6和申请号201010589305.2公开的假肢膝关节运动的控制方法均属于专家控制，前者通过霍尔传感器判定步态、步速后直接给出设定好的控制信号来控制假肢的行走。后者建立了下肢假肢自动训练专家知识库的方法，提出了使用迭代学习的方法来寻找使得假肢和健肢侧步态周期相差最小，在不同步态下对称性最好的假肢膝关节控制量来进行假肢控制。以上两种方案中的控制方法无法做到实时控制信号的调节，一旦系统由于各种原因出现扰动，就会导致控制效果变差。

鉴于现有假肢运动控制技术中存在的上述缺陷，对于主动型假肢的控制需要研发一种控制精度高、抗干扰能力强并且有较好时效性的控制方法。

技术实现要素：

针对现有技术的不足，本发明拟解决的技术问题是，提供一种基于干扰观测器的主动型膝上假肢终端滑模控制方法。该方法离线采集患者的基本信息数据，生成数据报告；在不改变基本构造和相互作用方式的前提下，将人体下肢简化为二连杆模型进行分析，针对人体行走过程中摆动期和支撑期的运动形式的差异，得出支撑期和摆动期的下肢动力学模型；对下肢动力学模型设计干扰观测器和终端滑模控制器。该方法将滑模变结构控制理论引入到主动型膝上假肢的控制中，在保留了传统滑模控制的抗干扰能力和快速响应等优点的同时，削弱了控制量的抖振程度，使模型系统的跟踪误差能够在有限时间内收敛到零。

本发明解决所述技术问题的技术方案是，提供一种基于干扰观测器的主动型膝上假肢终端滑模控制方法，其特征在于该方法包括以下步骤：

第一步，离线采集患者的基本信息数据，生成数据报告；

在患者膝关节、大腿、小腿、踝关节、脚趾和足跟六个部位左右侧各粘贴一个表面涂有反光物质的红外反光球；通过viconmx三维步态分析系统中的mx红外拍摄头捕捉红外反光球的运动轨迹，将患者的身高、体重、腿长、骻宽度、膝关节宽度和踝关节宽度数据传输到pc主机的viconmx三维步态分析系统软件中获取患者在不同路况条件下的膝关节角度信号和踝关节角度信号，并生成数据报告；

第二步，建立人体下肢动力学模型；

在人体正常行走时，根据行走过程中足部是否与地面接触，可将一个步态周期分为支撑期和摆动期；

当人体下肢处于摆动期时，摆动期下肢动力学模型简化为二连杆模型，对于该二连杆模型，摆动期的动力学模型如下：

其中，

g1＝(mst1rst1+mst2lst1)gcos(qst1)+mst2rst2gcos(qst1+qst2)

g2＝mst2rst2gcos(qst1+qst2)

其中大腿部分和小腿部分长度分别以lst1、lst2表示，大腿部分和小腿部分质心位置分别以rst1、rst2表示，髋关节部分和膝关节部分的角位移分别以qst1、qst2表示，髋关节部分和膝关节部分的角速度分别以表示，髋关节部分和膝关节部分的角加速度分别以表示，大腿和小腿质量分别用mst1、mst2，髋关节和膝关节力矩分别以τst1、τst2表示；

摆动期的控制主要在于膝关节的控制，由式(1)可以得到摆动期膝关节力矩为：

将髋关节角度看做随时间变化的函数，对式(2)进行整理，可以得到摆动期的动力学模型如下：

其中，qst＝qst2，hst＝0，tst＝τst2，

当人体下肢处于支撑期时，支撑期下肢动力学模型简化为二连杆模型，对于该二连杆模型，其动力学模型与摆动期的形式相同，但是在支撑期需要考虑人体躯干的重力在膝关节处产生的力矩；由于踝关节主要起到支撑作用，不提供主动力，因此不对踝关节进行控制，由此可以得到支撑期膝关节力矩为：

将踝关节角度看做随时间变化的函数，对式(4)进行整理，可以得到支撑期的动力学模型如下：

其中，qsw＝qsw2，hsw＝0，tsw＝τsw2，

th＝-m3gcos(qsw1+qsw2)

其中小腿部分和大腿部分长度分别以lsw1、lsw2表示，小腿部分和大腿部分质心位置分别以rsw1、rsw2表示，踝关节部分和膝关节部分的角位移分别以qsw1、qsw2表示，踝关节部分和膝关节部分的角速度分别以表示，踝关节部分和膝关节部分的角加速度分别以表示，小腿和大腿质量分别用msw1、msw2，踝关节和膝关节力矩分别以τsw1、τsw2表示，th为人体躯干的重力在膝关节处的力矩，m3为人体躯干部分的质量；

可以看出支撑期和摆动期的下肢动力学模型如式(6)，

第三步，干扰观测器的设计；

设动力学模型系统存在外界干扰d，令x1＝q，u＝t为膝关节的输入力矩，动力学模型系统如下：

对动力学模型系统设计干扰观测器如下：

其中是干扰观测器对x2的估计值，是对d的估计值，k1、k2是干扰观测器的系数，记

下面分析干扰观测器对干扰观测的准确程度：

设d为慢时变信号，因此的值很小，当k1取较大时，则有那么可以得到：

当k2＞0时，当时，因此当t→∞时，表明通过采用该观测器，能够对d进行有效的观测，从而实现对动力学模型系统扰动的补偿；

第四步，终端滑模控制器的设计；

终端滑模控制的滑模面选择为：

其中c为滑模系数；e为跟踪误差；为了保证终端滑模控制系统的全局鲁棒性，对于p(t)须有：当t＝0时，p(0)＝e(0)，为了确保终端滑模控制系统能够在t时刻跟踪上期望输出，p(t)应满足当t＝t时，p(t)＝0，构造如下p(t)多项式：

由t＝t时，p(t)＝0，解得：

对滑模面s求导可得：

其中x1d为期望输出，e＝x1-x1d，

因此控制律设计为：

其中

将us带入式(13)可以得到

终端滑模控制系统的稳定性分析过程如下：

首先取李雅普诺夫函数为：

对于李雅普诺夫函数，其导数为：

取闭环系统的李雅普诺夫函数为v＝v1+v2，根据式(9)和式(15)可得：

当时，s≡0根据李雅普诺夫稳定性判据，终端滑模控制系统稳定；

由于p(0)＝e(0)，所以s(0)＝0，表明终端滑模控制系统在初始时刻已经在滑模面上，从而保证了终端滑模控制系统的全局稳定性和鲁棒性；设计p(t)＝0，是为了保证e(t)＝0，并且满足式(11)求解的需要，从而保证跟踪误差在规定时间内收敛到零。

与现有技术相比，本发明有益效果在于：

(1)相较于专家控制，专家控制只能根据传感器信号判断出当前运动状态所属的阶段进而基于对应的控制模型计算出控制量，其控制目标是按照专家系统预先设计好的轨迹进行运动，是一种分段开环控制方法，无法根据外界干扰进行相应调节，一旦系统中由于各种原因出现扰动，就会导致控制效果变差。本方法属于闭环控制，可以根据外界干扰进行相应调节，有更好的鲁棒性和抗干扰能力，能对假肢有更好的控制效果。

(2)相较于神经网络控制，由于神经网络需要对假肢系统的数学模型进行在线辨识，而神经网络的结构一般比较复杂，复杂的网络结构会增加微处理器的运行负担，使控制过程的实时性变差。本方法响应速度快，无需系统在线辨识，能跟踪复杂的非线性系统，用于主动型下肢假肢的控制中具有很好的实时性。

(3)滑模控制具有快速响应、对参数变化及扰动不灵敏、能跟踪复杂的非线性系统等优点，但也存在引起系统抖振、跟踪误差无法在有限时间收敛到零的缺点，抖振会影响控制的精度，增加能量的消耗，甚至损坏控制器的执行机构。本方法通过设计干扰观测器对模型系统的误差和外界干扰进行估计并补偿，削弱了控制量的抖阵程度；通过设计非线性的终端滑模面，保证了模型系统的全局稳定性和鲁棒性，并且使跟踪误差能够在规定时间内收敛到零。

附图说明

图1为本发明基于干扰观测器的主动型膝上假肢终端滑模控制方法一种实施例的下肢摆动期动力学模型示意图；

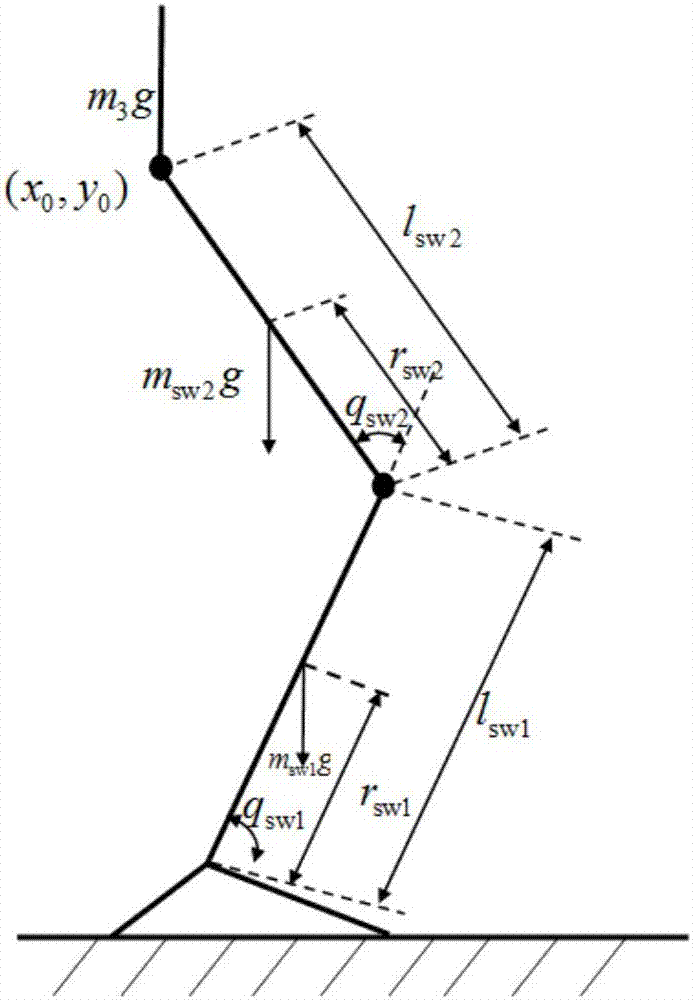
图2为本发明基于干扰观测器的主动型膝上假肢终端滑模控制方法一种实施例的下肢支撑期动力学模型示意图；

图3为正常人平地行走时髋关节、膝关节和踝关节角度曲线图；

图4为本发明基于干扰观测器的主动型膝上假肢终端滑模控制方法实施例1的控制效果图；(其中：图4(a)为平地行走时终端滑模控制器跟踪目标曲线效果图；图4(b)为平地行走时干扰观测器对扰动的观测效果图；图4(c)为平地行走时干扰观测器的误差曲线)

图5为本发明基于干扰观测器的主动型膝上假肢终端滑模控制方法实施例2的控制效果图；(其中：图5(a)为上楼梯时终端滑模控制器跟踪目标曲线效果图；图5(b)为上楼梯时干扰观测器对扰动的观测效果图；图5(c)为上楼梯时干扰观测器的误差曲线)

图6为本发明基于干扰观测器的主动型膝上假肢终端滑模控制方法实施例3的控制效果图；(其中：图6(a)为下楼梯时终端滑模控制器跟踪目标曲线效果图；图6(b)为下楼梯时干扰观测器对扰动的观测效果图；图6(c)为下楼梯时干扰观测器的误差曲线)

图7为本发明基于干扰观测器的主动型膝上假肢终端滑模控制方法实施例4的控制效果图；(其中：图7(a)为上斜坡时终端滑模控制器跟踪目标曲线效果图；图7(b)为上斜坡时干扰观测器对扰动的观测效果图；图7(c)为上斜坡时干扰观测器的误差曲线)

图8为本发明基于干扰观测器的主动型膝上假肢终端滑模控制方法实施例5的控制效果图；(其中：图8(a)为下斜坡时终端滑模控制器跟踪目标曲线效果图；图8(b)为下斜坡时干扰观测器对扰动的观测效果图；图8(c)为下斜坡时干扰观测器的误差曲线)

图9为使用matlab7.0软件中的simulink模块对控制过程进行仿真验证的结构图；

具体实施方式

下面给出本发明的具体实施例。具体实施例仅用于进一步详细说明本发明，不限制本申请权利要求的保护范围。

本发明提出了一种基于干扰观测器的主动型膝上假肢终端滑模控制方法(简称方法)，其特征在于该方法包括以下步骤：

第一步，离线采集患者的基本信息数据，生成数据报告；

利用国家康复辅具研究中心的vicon步态分析系统对患者下肢运动信息进行采集；vicon系统采用了被动式光学运动捕捉的原理，在患者膝关节、大腿、小腿、踝关节、脚趾和足跟六个部位左右侧各粘贴一个表面涂有反光物质的红外反光球；通过viconmx三维步态分析系统中的mx红外拍摄头捕捉红外反光球的运动轨迹，将患者的身高、体重、腿长、骻宽度、膝关节宽度和踝关节宽度数据传输到pc主机的viconmx三维步态分析系统软件中，先初始化建立静态模型并仿真出行走视频，生成完整的步态数据，最后加载动态模型，用polygon软件导出数据，最终获取患者在不同路况条件下的髋关节、膝关节和踝关节角度信号，并生成数据报告；其中数据传输过程为：任一个红外反光球被两台mx红外拍摄头同时所见，根据此刻mx红外拍摄头拍摄的图像和mx红外拍摄头参数，即可确定该点的位置，进而捕捉红外反光球的运动轨迹；mx红外拍摄头将数据通过mxnet传输到mxlink中，最后数据经由mxlink传输至pc主机中的viconmx三维步态分析系统的软件部分中；

viconmx三维步态分析系统包括硬件部分和软件部分；所述硬件部分包括六个mx红外拍摄头、mxnet、mxlink、mxcontrol和pc主机；所述mx红外拍摄头通过mxnet与mxlink连接；所述mxlink与pc主机连接；mxnet与mxcontrol连接；mxnet用于为mx红外拍摄头提供电源，且使mx红外拍摄头与pc主机或mxlink进行数据交换；mxlink具有增强数据传输的功能；vicon软件均安装于该pc主机内；所述软件部分中的workstation是vicon系统核心处理软件，用于设置和校准vicon动作捕捉系统，捕捉和处理动作数据。workstation利用各mx红外拍摄头处理后图像数据，综合校准数据，重新生成3d动作数据。在此软件中能够查阅和控制此3d数据，还可以传递至其它vicon操作软件，进行分析和使用，或者送至第三方应用装置，如用于数字动画或虚拟环境中进行后续操作。

第二步，建立人体下肢动力学模型；

在人体正常行走时，根据行走过程中足部是否与地面接触，可将一个步态周期分为支撑期和摆动期；其中，支撑期是指足部与地面接触的时期，支撑身体的重量实现重心转移；摆动期是指支撑期过后，足部完全腾空的时期；因为人体行走过程中摆动期和支撑期的运动形式存在较为明显的差异，所以下面分别对摆动期和支撑期进行动力学建模；

当人体下肢处于摆动期时，摆动期下肢动力学模型简化为二连杆模型如图1所示，对于该二连杆模型，摆动期的动力学模型如下：

其中，

g1＝(mst1rst1+mst2lst1)gcos(qst1)+mst2rst2gcos(qst1+qst2)

g2＝mst2rst2gcos(qst1+qst2)

其中大腿部分和小腿部分长度分别以lst1、lst2表示，大腿部分和小腿部分质心位置分别以rst1、rst2表示，髋关节部分和膝关节部分的角位移分别以qst1、qst2表示，髋关节部分和膝关节部分的角速度分别以表示，髋关节部分和膝关节部分的角加速度分别以表示，大腿和小腿质量分别用mst1、mst2，髋关节和膝关节力矩分别以τst1、τst2表示；

对于膝上截肢的残疾人而言，其大腿部分仍保留有部分残肢，可以认为其髋关节功能是正常的，无需控制；摆动期的控制主要在于膝关节的控制，由式(1)可以得到摆动期膝关节力矩为：

将髋关节角度看做随时间变化的函数，对式(2)进行整理，可以得到摆动期的动力学模型如下：

其中，qst＝qst2，hst＝0，tst＝τst2，

当人体下肢处于支撑期时，支撑期下肢动力学模型简化为二连杆模型如图2所示，对于该二连杆模型，其动力学模型与摆动期的形式相同，但是在支撑期需要考虑人体躯干的重力在膝关节处产生的力矩；由于踝关节主要起到支撑作用，不必提供主动力，因此可以不对踝关节进行控制，由此可以得到支撑期膝关节力矩为：

将踝关节角度看做随时间变化的函数，对式(4)进行整理，可以得到支撑期的动力学模型如下：

其中，qsw＝qsw2，hsw＝0，tsw＝τsw2，

th＝-m3gcos(qsw1+qsw2)

其中小腿部分和大腿部分长度分别以lsw1、lsw2表示，小腿部分和大腿部分质心位置分别以rsw1、rsw2表示，踝关节部分和膝关节部分的角位移分别以qsw1、qsw2表示，踝关节部分和膝关节部分的角速度分别以表示，踝关节部分和膝关节部分的角加速度分别以表示，小腿和大腿质量分别用msw1、msw2，踝关节和膝关节力矩分别以τsw1、τsw2表示，th为人体躯干的重力在膝关节处的力矩，m3为人体躯干部分的质量；

可以看出支撑期和摆动期的下肢动力学模型如式(6)，

因此在设计干扰观测器和控制律时，在支撑期和摆动期所采用的方法是相同的；

第三步，干扰观测器的设计；

设动力学模型系统存在外界干扰d，令x1＝q，u＝tu＝t为膝关节的输入力矩，动力学模型系统如下：

对动力学模型系统设计干扰观测器如下：

其中是干扰观测器对x2的估计值，是对d的估计值，k1、k2是干扰观测器的系数，记

下面分析干扰观测器对干扰观测的准确程度：

设d为慢时变信号，因此的值很小，当k1取较大时，则有那么可以得到：

当k2＞0时，当时，因此当t→∞时，表明通过采用该观测器，能够对d进行有效的观测，从而实现对动力学模型系统扰动的补偿；

第四步，终端滑模控制器的设计；

终端滑模控制的滑模面选择为：

其中c为滑模系数；e为跟踪误差；为了保证终端滑模控制系统的全局鲁棒性，对于p(t)须有：当t＝0时，p(0)＝e(0)，为了确保终端滑模控制系统能够在t时刻跟踪上期望输出，p(t)应满足当t＝t时，p(t)＝0，构造如下p(t)多项式：

由t＝t时，p(t)＝0，解得：

对滑模面s求导可得：

其中x1d为期望输出，e＝x1-x1d，

因此控制律设计为：

其中

将us带入式(13)可以得到

终端滑模控制系统的稳定性分析过程如下：

首先取李雅普诺夫函数为：

对于李雅普诺夫函数，其导数为：

取闭环系统的李雅普诺夫函数为v＝v1+v2，根据式(9)和式(15)可得：

当时，s≡0根据李雅普诺夫稳定性判据，终端滑模控制系统稳定；

由于p(0)＝e(0)，所以s(0)＝0，表明终端滑模控制系统在初始时刻已经在滑模面上，从而保证了终端滑模控制系统的全局稳定性和鲁棒性；设计p(t)＝0，是为了保证e(t)＝0，并且满足式(11)求解的需要，从而保证跟踪误差在规定时间内收敛到零。

在干扰观测器与终端滑模控制器设计好后，使用matlab7.0软件中的simulink模块对主动型膝上假肢终端滑模控制进行平地行走仿真验证，其结构如图9所示。图中左侧为控制假肢运动所需要的数据，分别为膝关节角度、踝关节角度和髋关节角度。右侧为基于干扰观测器的终端滑模控器的结构。ndo为非线性干扰观测器，tsmc为终端滑模控制器，plane为主动型膝上假肢模型，ytsmc为假肢模型系统的输出，输出的量是膝关节角度。

主动型膝上假肢模型中的参数包括人体各体段的质量、长度以及质心位置，这些参数可以通过国家质量监督检验检疫总局和国家标准化管理委员会联合发布的gb/t19245-2004《成年人人体惯性参数》和gb/t10000-88《成年人人体尺寸》两项国家标准计算得到，实施例1-5中取小腿长度lsw1＝lst2＝0.39m，大腿长度lst1＝lsw2＝0.42m，小腿质量msw1＝mst2＝2.2kg，大腿质量mst1＝msw2＝8.5kg，躯干质量m3＝36.71kg，小腿质心位置rsw1＝0.22m，rst2＝0.17m，大腿质心位置rsw2＝0.25m，rst1＝0.17m。所需的角度数据利用国家康复辅具研究中心的vicon步态分析系统对下肢运动信息进行采集，平地行走时髋关节、膝关节和踝关节角度如图3所示。

在实施例1-5中，由于动力学模型过于复杂时会对终端滑模控制器的设计带来很大的困扰，并且影响控制器的稳定性，为了简化动力学模型，在建模的时候没有将踝关节力矩考虑进去，因此将其当做未建模动态，看成“干扰”，并使用干扰观测器进行观测，踝关节力矩记为ta，令d＝ta。

实施例1

取滑模系数c＝0.1，干扰观测器系数k1＝1000，k2＝20，收敛时间t＝1s对平地行走进行仿真控制。图4(a)是平地行走时终端滑模控制器的控制效果，从图中可见，在平地行走时终端滑模控制器有很好的控制效果，能够快速、精确的跟踪上正常人行走时的角度曲线。图4(b)是平地行走时干扰观测器的估计值与实际值的对比，图4(c)是干扰观测器的误差曲线，可以看出干扰观测器的估计值很好的逼近了实际值，并且两者的误差在-0.04n·m/kg～0.04n·m/kg之间，对于实际值很小，在误差允许范围内。

实施例2

取滑模系数c＝0.1，干扰观测器系数k1＝800，k2＝15，输入上楼梯时髋关节、膝关节和踝关节角度，对上楼梯过程进行仿真验证，结果如图5(a)、图5(b)、图5(c)所示，可以看出干扰观测器能有效地对干扰进行观测，终端滑模控制器能够快速、精确的跟踪上正常人行走时的角度曲线。

实施例3

取滑模系数c＝0.1，干扰观测器系数k1＝800，k2＝20，输入下楼梯时髋关节、膝关节和踝关节角度，对下楼梯过程进行仿真验证，结果如图6(a)、图6(b)、图6(c)所示，可以看出干扰观测器能有效地对干扰进行观测，终端滑模控制器能够快速、精确的跟踪上正常人行走时的角度曲线。

实施例4

取滑模系数c＝0.2，干扰观测器系数k1＝1000，k2＝15，输入上斜坡时髋关节、膝关节和踝关节角度，对上斜坡过程进行仿真验证，结果如图7(a)、图7(b)、图7(c)所示，可以看出干扰观测器能有效地对干扰进行观测，终端滑模控制器能够快速、精确的跟踪上正常人行走时的角度曲线。

实施例5

取滑模系数c＝0.2，干扰观测器系数k1＝1000，k2＝20，输入下斜坡时髋关节、膝关节和踝关节角度，对下斜坡过程进行仿真验证，结果如图8(a)、图8(b)、图8(c)所示，可以看出干扰观测器能有效地对干扰进行观测，终端滑模控制器能够快速、精确的跟踪上正常人行走时的角度曲线。

从以上实验结果可以看出：对于五种地形，干扰观测器均能有效地对干扰进行观测，终端滑模控制器均有很好的控制效果，能够快速、精确的跟踪上正常人行走时的角度曲线。

本发明未述及之处适用于现有技术。