一种癫痫患者脑电信号的处理方法及系统与流程

本发明提供一种癫痫患者脑电信号的处理方法，属于非线性生理信号处理
技术领域：
。
背景技术：
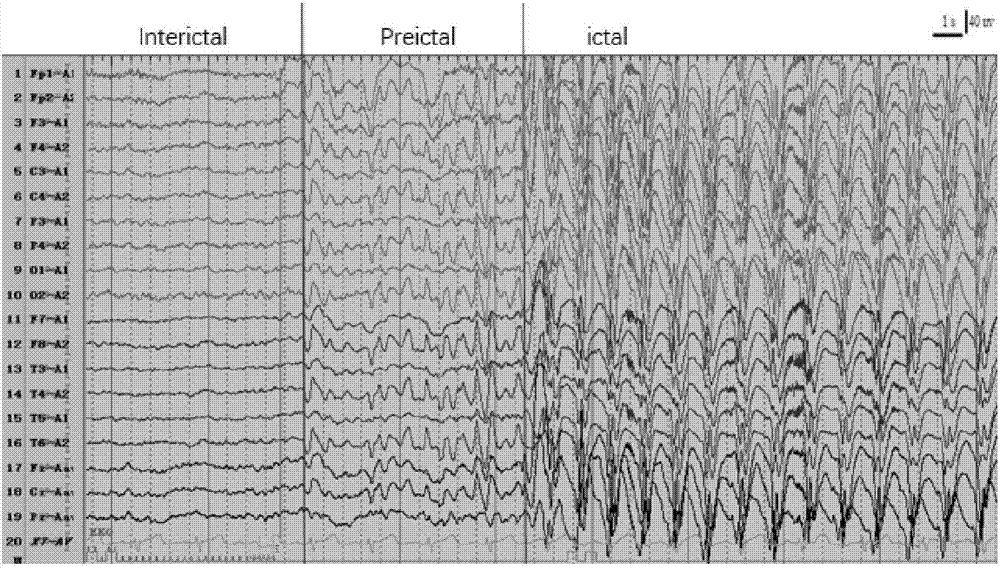
：癫痫是一种常见的、多发的慢性神经系统疾病，其发作是由于大脑的神经元活动的同步或过多而引起的神经元不规则和不规则的放电而引起的。在癫痫发作过程中，会引起运动、行为、意识和感觉等功能障碍，因此，癫痫发作可能导致各种致命的后果。全世界有超过5000万人患有癫痫，每年有超过200000例新发病例被确诊。癫痫的治疗手段有手术、药物、电刺激等方法，而在确定治疗手段之前，最关键的在于对疑似癫痫病人的检测。目前，癫痫的检测方法是基于医生的视觉检测，由于需要对病人的脑电信号进行长时间的检测，因此传统的医生检测方法是非常耗时耗力的，很多医院甚至由于相关医生不足导致检测速度过慢而耽误了病人的最佳治疗时机。另一方面，由于传统的癫痫检测依赖于医生的肉眼观察与主观判断，有时容易出错，这可能会导致意外的误诊。因此，迫切需要开发一种癫痫发作的自动检测方法，来减轻医生的工作量，同时也减少肉眼检测产生的误差而造成的误诊。故癫痫发作检测的自动化检测方法在临床上具有重要的应用价值。脑电(electroencephalogram，eeg)被广泛应用在癫痫检测分析中，人体脑电信号由上亿的神经元相互作用形成，因而具有时变、非线性、不稳定等特点，同时脑电数据信号在测量后会产生随机误差，并且脑电信号还会受到个体差异的影响，因此，对于脑电数据信号的分析成为难题。现存有多种癫痫信号预警的方法，但由于癫痫脑电信号本身的复杂性，导致各种算法的准确性、敏感性和特异性方面都存在各种各样的缺点，如准确性高了，特异性就降低等问题。另外，以往算法一般都只利用了单导脑电信号而忽略了同时采集的其他导脑电信号，容易造成提取的特征无法反映病人大脑的全局病理特性以及所有脑电信号之间的时间-空间关系，如当病人从一种状态(发作间歇期、发作期)进入到另外一种状态，在同一时刻不同部位采集到的脑电是具有不同特征的。因此现有脑电信号的处理方法无法准确检测患者的癫痫发作。技术实现要素：针对现有癫痫检测算法在准确性、敏感性、特异性方面存在的不足以及大多数算法只利用单导脑电信号的问题，本发明提供了一种基于多导脑电信号的癫痫患者脑电信号的处理方法。本发明的目的是通过以下技术方案实现的，一种癫痫患者脑电信号的处理方法，具体步骤包括：1)获取不含噪声的癫痫患者的多导脑电信号；2)将上述多导脑电信号分成若干数据段，采用最大互相关函数计算同一时间窗下的任意两段数据段的最大互相关系数，作为相应数据段的特征值，通过计算所有脑电信号之间的互相关系数构成特征矩阵；3)从互相关系数构成的特征矩阵中去除背景噪声特征，获取与癫痫发作相关的稀疏特征矩阵，作为最终的脑电信号的特征矩阵；4)采用最小二乘支持向量机算法分类癫痫患者脑电信号。进一步，本发明还可以采用kofn分析法来进一步校正经过最小二乘支持向量机分类的结果。作为一种优选方案，去除脑电信号噪声采用的离散小波变换方法是采用daubeches-4小波函数，滤波后选取频率为3～25hz波段的脑电信号。作为一种优选方案，将脑电信号分成若干数据段具体为：采用滑动时间窗的方法将任意两导脑电信号分为若干数据段，滑动时间窗长度为0.1s，滑动步长为0.05s，相邻的两时间窗有50％的重叠。作为一种优选方案，采用最大互相关函数计算最大互相关系数，具体为：将在同一时间窗的任意两导脑电信号数据段，利用下式计算得到每个数据段的最大互相关系数：其中n是时间窗的宽度(在本例中,n＝100)；ci,j是两导脑电信号的最大相关系数，取值范围为[-1，1]；τ表示两导脑电信号的不同步造成时间上的延迟长度；(xi,xj)表示两导脑电数据段；i,j表示两导脑电信号每个数据段的数据点的序数。作为一种优选方案，计算互相关系数构成特征矩阵具体为：将每个数据段计算得到的ci,j按照时间顺序依次排列构成特征矩阵d。作为一种优选方案，采用鲁棒性主成分分析法来获取与癫痫发作相关的稀疏特征矩阵，作为最终的相应脑电信号的特征矩阵,具体为：将最大相互关系数矩阵d采用鲁棒性主成分分析法分解为低秩矩阵a与稀疏矩阵e之和，其中低秩矩阵a表示脑电信号背景信息，稀疏矩阵e表示与癫痫发作相关的特征，稀疏矩阵e作为最终脑电信号的特征矩阵。作为一种优选方案，所述最小二乘支持向量机算法训练方法如下：将癫痫患者脑电信号数据库，随机分成70％与30％两部分，用70％的脑电数据来训练算法，用剩余的30％数据来测试算法，从而得到最小二乘支持向量机模型。作为一种优选方案，采用kofn分析法具体为：在连续n个数据段中至少有k个数据段被判断为发作，则将全部n个数据段视为癫痫发作作态，否则将n个数据段视为发作间歇期。本发明的有益效果是，本发明采用最大相关函数法计算得到每个数据段的最大相关系数矩阵；并采用鲁棒性主成分分析法，将特征矩阵进行分解，得到了与癫痫相关的稀疏特征矩阵，去除了背景噪声，使得特征矩阵更能反应癫痫发作相关特征；再采用最小二乘支持向量机算法分类癫痫患者脑电信号。本发明可以将癫痫发作与发作间歇期的判断转化为二分类问题，计算复杂度低，实时性好，同时准确度更高，可以用于快速识别脑电信号的特征变化并实时监测癫痫发作与否，实现癫痫发作的检测。通过本发明所提供的基于多导脑电信号的癫痫发作检测方法，应用于癫痫患者eeg信号，实现了癫痫检测的极高的准确性、敏感性和特异性。附图说明图1是本发明具体实施例的框图；图2是癫痫发作间歇期与发作期的原始脑电信号图；图3是经最小二乘支持向量机分类的癫痫发作前后脑电信号分类结果；图4是经kofn分析法后处理的癫痫发作前后脑电信号分类结果。具体实施方式下面结合附图对本发明作进一步详细说明。如图1所示，本发明基于多导脑电信号的癫痫患者脑电信号的处理系统，包括预处理模块、特征提取模块、特征选择模块、分类模块和后处理模块：(1)预处理模块对脑电数据进行预处理，将原始的19导脑电数据(如图2所示)逐一通过daubeches-4小波函数滤波去噪，滤波后选取频率为3～25hz波段的脑电信号。(2)特征提取模块将经过预处理之后的脑电信号分成若干数据段，具体为：采用滑动时间窗的方法将任意两导脑电信号分为若干数据段，滑动时间窗长度为0.1s，滑动步长为0.05s，相邻的两时间窗有50％的重叠。然后采用最大互相关函数计算最大互相关系数，具体为：将在同一时间窗的任意两导脑电信号数据段，利用下式计算得到每个数据段的最大互相关系数：其中n是时间窗的宽度(在本例中,n＝100)；ci,j是两导脑电信号的最大相关系数，取值范围为[-1，1]；τ表示两导脑电信号的不同步造成时间上的延迟长度；(xi,xj)表示两导脑电数据段；i,j表示两导脑电信号每个数据段的数据点的序数。对19导脑电数两两计算最大互相关系数，最终每一时间窗下，一共有19×(19-1)/2个最大互相关系数以及19个自相关系数，将这190个系数拉成一列，构成特征矩阵的一列。按照时间轴正向移动时间窗，计算脑电信号的全部相关系数，按照时间顺序依次排列，构成相关系数矩阵d。(3)特征选择模块本发明采用鲁棒性主成分分析法选择特征矩阵。鲁棒性主成分分析法能有效减少噪声特征的影响，同时有效消除异常值对投影矩阵的影响。本发明将特征提取模块中获得的相关系数矩阵d∈rm×n(m表示参数值，n表示采样数量)采用鲁棒性主成分分析法分解为低秩矩阵a与稀疏矩阵e之和，其中低秩矩阵a表示脑电信号背景信息，稀疏矩阵e表示与癫痫发作相关的特征，稀疏矩阵e作为最终脑电信号的特征矩阵。具体如下：该问题可以转化为：minl,s‖a‖*+λ‖e‖1,subjecttoa+e＝d,其中‖a‖*表示矩阵的核范数，‖e‖1表示矩阵的值，λ是正权重参数，取值为采用非精确增广拉格朗日乘子法求解该问题，具体如下：定义：x＝(a,e),f(x)＝‖a‖*+λ‖e‖1,h(x)＝d-a-e.则该拉格朗日函数为：其中y∈rm×n表示拉格朗日乘数矩阵，μ表示正值常数，<·,·>表示矩阵内积，表示frobenius范数。求解该问题的算法具体如下：输出的ak,ek即为所要求解的低秩矩阵a与稀疏矩阵e，其中稀疏矩阵e就是索要求的与癫痫相关的特征矩阵，作为最终输入到分类模块中的特征值。实验结果显示，使用稀疏矩阵e作为分类模型的输入比直接使用相关系数矩阵d作为分类模型的数据具有更高的准确性。(4)分类模块本发明采用最小二乘支持向量机判断脑电信号的发作状态。最小二乘支持向量机(leastsquaressupportvectormachine，ls-svm)是一种用改进的支持向量机，克服了支持向量机的高计算负担的缺点，具有更强的实时性，经常被使用来生理信号的识别分类，是一种二元分类器。构造最小二乘支持向量机的过程是用最小二乘法求解一个二次规划问题，找到分开两类训练数据的最优超平面过程。所谓最优超平面，是指分类面不仅能正确地分开两类数据，还能使两类之间的间隔最大。当输入n对数据(其中xi∈rn是第i个输入特征，yi∈r是对应的第i个类别标注，即对应的脑电信号发作状态)，可以通过下面的决策函数f(x)对其类别进行判定：其中αi为训练得到的拉格朗日因子，b是分类阈值，k(x,xi)是核函数。常见的核函数有线性核函数、poly核函数、mlp核函数和rbf核函数等，本发明比较了线性核函数、poly核函数、mlp核函数和rbf核函数之后，选择效果最好的rbf核函数。最小二乘支持向量机类的准确性取决于训练模型的质量，本发明选取初次发作的脑电数据建立最优训练模型。首先，依照前述预处理和特征提取、特征选择的流程处理脑电数据。训练方法如下：将癫痫患者脑电信号数据库，随机分成70％与30％两部分，用70％的脑电数据来训练算法，用剩余的30％数据来测试算法，从而得到最小二乘支持向量机模型及其相关性能指标。(5)后处理模块对经过最小二乘支持向量机模型分类之后的结果(如图3所示)采用kofn分析法进行后处理，具体为：在连续n个点中至少有k个点被判断为发作，则将全部n个点视为癫痫发作作态，否则将n个点视为发作间歇期。经过后处理之后的分类结果(如图4所示)，与未进行后处理的分类结果(如图3所示)相比较，在敏感度、特异性与准确性上有了较大的提高。实验结果采用本方法，利用北京大学第一医院癫痫诊断中心的已有的癫痫患者的脑电数据库，脑电信号全部采用nihonkohden数字视频eeg系统采集，包含19导的时域脑电信号。取其中37位患者，共57次发作的全部脑电数据，以及57×5分钟发作间歇期的脑电信号。全部脑电信号由北京大学第一医院的癫痫专家标记，将癫痫发作间歇期脑电信号标记为“0”类，将发作期脑电信号标记为“1”类。本次试验分别用三个指标评价分类性能，特异性(specificity)、敏感度(sensitivity)和准确率(accuracy)。三个指标的计算公式如下：其中tp,fp,tn,和fn分别表示真阳个数，假阳个数，真阴个数，假阴个数。将发作与发作间歇期的脑电数据分别随机分成70％与30％两份，对最小二乘支持向量机模型进行训练并测试其性能，具体结果见下表所示。从表中数据可知，使用rbf核函数的效果最好，而使用线性核函数的效果最差。表4种不同核函数下最小二乘支持向量机模型分类结果核函数类型敏感度(％)特异性(％)准确性(％)线性核函数50.455.147.3poly核函数95.581.090.5mlp核函数93.098.095.5rbf核函数98.0100.099.0脑电信号对癫痫研究具有重要价值，本发明使用基于多导脑电信号的癫痫发作检测方法癫痫患者脑电信号做了详细分析，敏感性为98.0％，特异性为100.0％,准确性为99.0％。本发明不局限于上述实施例所述的具体技术方案，凡采用等同替换形成的技术方案均为本发明要求的保护。当前第1页12