一种用于预测汽油辛烷值的方法与流程

本发明涉及石油化工领域，具体地涉及一种用于预测汽油辛烷值的方法。

背景技术：

汽油由多种组分调合而成，本申请发明人在实现本发明的过程中发现，无论这里的调合组分是指纯烃化合物还是某种组分油，调合过程中辛烷值都会呈现较明显的非线性规律。可以说，汽油辛烷值不仅与汽油中各调合组分自身的辛烷值有关，也与调合过程中各组分调合特性有关。近年来，在油品升级过程中，更多强调的是高辛烷值组分的添加比例，而相对忽视了调合过程中非线性调合效应可能对汽油辛烷值造成的贡献或者损失。而基于详细组成的辛烷值预测模型旨在解决这一难题，在分子水平上对汽油辛烷值进行认识的同时，达到辛烷值较高精度预测的目标。而这一模型建立的核心则是汽油组成-辛烷值数学表达关系的建立。

目前国内外一些研究机构给出了少量辛烷值与汽油组成数学关系的猜想，然而这些模型多由实验规律做出的假设推论而来，欠缺对辛烷值调合过程的深入认识及理论研究，受限于实验方法的基础，所得模型也有预测精度及适用范围方面的不足。

技术实现要素：

本发明实施例的目的是提供一种用于预测汽油辛烷值的方法，其可改善汽油辛烷值的预测精度。

为了实现上述目的，本发明实施例提供一种用于预测汽油辛烷值的方法，该方法包括：根据所述汽油内各组分及活性核转化率计算模型，计算活性核转化率；以及根据所述活性核转化率以及辛烷值计算模型，计算所述汽油辛烷值。

可选的，在根据所述活性核转化率以及辛烷值计算模型计算所述汽油辛烷值该之前，该方法还包括：根据所述汽油内各组分的相互作用关系及活性转化率校正模型，对所述活性核转化率进行校正。

另一方面，本发明提供一种机器可读存储介质，该机器可读存储介质上存储有指令，该指令用于使得机器执行本申请上述预测汽油辛烷值的方法。

辛烷值是正庚烷和异辛烷的量进行参比的、反应汽油抗爆震能力的指标。本案发明人认识：1)辛烷值是一个相对概念；2)辛烷值不止与汽油组成有关，还和燃烧过程中的反应化学相关，这是造成调合过程中辛烷值非线性的原因。本发明提供了一种汽油组成与辛烷值数学关系表达式的建立方法：借助研究烃类在气缸中的燃烧化学模型，分解燃烧过程，提出了体系中活性核转化率决定辛烷值大小的猜想，并以此为基础来计算辛烷值，从而可考虑到汽油中各调合组分调合过程中非线性调合效应可能对汽油辛烷值造成的贡献或者损失，使得汽油辛烷值的预测更为精确。

本发明实施例的其它特征和优点将在随后的具体实施方式部分予以详细说明。

附图说明

附图是用来提供对本发明实施例的进一步理解，并且构成说明书的一部分，与下面的具体实施方式一起用于解释本发明实施例，但并不构成对本发明实施例的限制。在附图中：

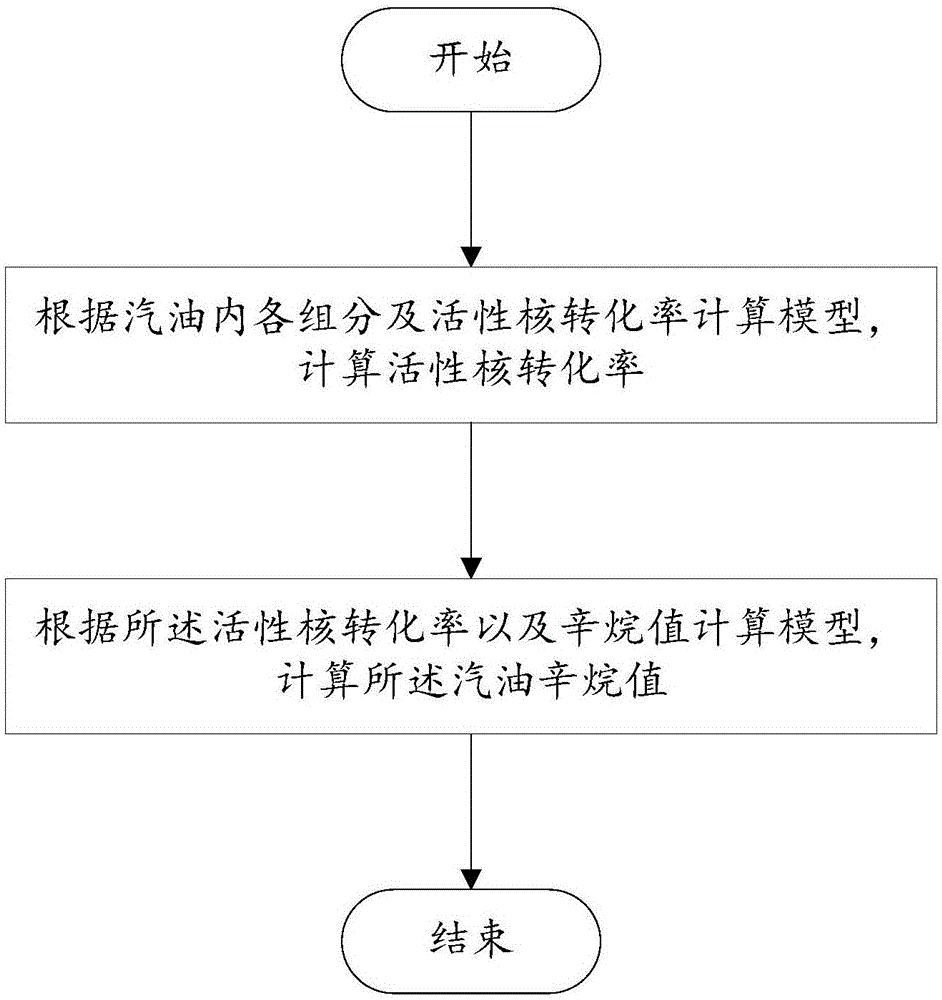
图1为本发明一实施例提供的用于预测汽油辛烷值的方法的流程图；

图2为本发明另一实施例提供的用于预测汽油辛烷值的方法的流程图；

图3为根据本发明第一实施例提供的用于预测汽油辛烷值的方法进行辛烷值预测的效果图；

图4为根据本发明第二实施例提供的用于预测汽油辛烷值的方法进行辛烷值预测的效果图；

图5为根据本发明第三实施例提供的用于预测汽油辛烷值的方法进行辛烷值预测的效果图；

图6a及图6b为根据本发明第四实施例提供的用于预测汽油辛烷值的方法进行辛烷值预测的效果图；

图7a及图7b为根据本发明第五实施例提供的用于预测汽油辛烷值的方法进行辛烷值预测的效果图；

图8为根据本发明第六实施例提供的用于预测汽油辛烷值的方法进行辛烷值预测的效果图；以及

图9为根据本发明第七实施例提供的用于预测汽油辛烷值的方法进行辛烷值预测的效果图。

具体实施方式

以下结合附图对本发明实施例的具体实施方式进行详细说明。应当理解的是，此处所描述的具体实施方式仅用于说明和解释本发明实施例，并不用于限制本发明实施例。

图1为本发明一实施例提供的用于预测汽油辛烷值的方法的流程图。如图1所示，本发明一实施例提供了用于预测汽油辛烷值的方法，该方法包括：根据所述汽油内各组分及活性核转化率计算模型，计算活性核转化率；以及根据所述活性核转化率以及辛烷值计算模型，计算所述汽油辛烷值。

该方案借助研究烃类在气缸中的燃烧化学模型，分解燃烧过程，提出了体系中活性核转化率决定辛烷值大小的猜想，并以此为基础来计算辛烷值，从而可考虑到汽油中各调合组分调合过程中非线性调合效应可能对汽油辛烷值造成的贡献或者损失，使得汽油辛烷值的预测更为精确。该方案借助燃烧机理，对汽油低温焰前燃烧反应过程进行简化，引入活性核转化率影响辛烷值的假设，把辛烷值模型建立分为活性核转化率的计算、活性核转化率的修正、以及辛烷值与活性核转化率的关联关系三个步骤进行各步骤建模，并最终组合成基于详细烃组成的辛烷值机理模型数学形式。

除了考虑各组分独自对体系中活性核转化率的影响外，在燃烧过程中各组分之间也会相互作用，增加新的活性核或惰性核生成途径，进而对体系内活性核转化率产生影响。图2为本发明另一实施例提供的用于预测汽油辛烷值的方法的流程图。优选地，如图2所示，在根据所述活性核转化率以及辛烷值计算模型计算所述汽油辛烷值该之前，该方法还包括：根据所述汽油内各组分的相互作用关系及活性转化率校正模型，对所述活性核转化率进行校正。

以下对上述技术方案中所涉及的三个模型进行分别介绍：

模型1：活性核转化率计算模型

具体而言，所述活性核转化率计算模型可选自以下中的一者，以计算体系内单位摩尔组分产生的活性核转化率qac：

模型1a：

其中，qac是单位摩尔组分产生的活性核转化率，[ni]表示i组分生成的活性核的含量，ni是i组分摩尔分数，υi是i组分体积分数，ki是低温焰前反应结束时，纯组分i生成活性核的转化率，βi是i组分的调合因子，其中，ρi是i组分的相对密度，mi是i组分的相对分子量。βi的取值最终需要通过实验数据进行回归，但通过简单推导可知，其值与i组分的密度和分子量的比值有关，由辛烷值定义可知，异辛烷和正庚烷的βi值为1，可以由此建立参比函数，获得每个组份的βi初值。

模型1b：

其中，ni·是i组分在低温焰前反应阶段产生的自由基摩尔分数，ni是i组分摩尔分数，θi是低温焰前反应阶段i组分生成自由基的反应速率，qi是i组分自由基进一步生成活性核的反应速率。该模型的建立基础是假设活性核与自由基的比值(即自由基变为活性核的能力)决定了辛烷值的大小。

模型1c：

其中，该模型1c内各参数的含义与上述模型1b内各参数的含义相同，该模型是在模型1b的基础上加入组分竞争氧化的猜想，参照吸附机理形成的模型。

模型2：活性转化率校正模型

除了考虑各组分独自对体系中活性核转化率的影响外，在燃烧过程中各组分之间也会相互作用，增加新的活性核或惰性核生成途径，进而对体系内活性核转化率产生影响。可通过对机理的不同假设，建立稳态方程，得到新增活性核与组成的函数关系。在此给出了2a、2b两种模型形式,可以计算出新增加的活性核数量，将其加入上述活性核转化率计算模型中，对活性核转化率qac完成修正。

所述活性转化率校正模型可选自以下中的一者，以对活性核转化率qac进行修正：

模型2a：

模型2a是由反应机理a建立的稳态方程推导而来的，稳态方程如2a’，其中，ki、分别是反应机理a的反应速率，ni、nj分别是i组分和j组分的摩尔分数，是i组分新增的活性核转化率。

反应机理a

该模型在考察某一组分燃烧反应时，假设其它组分作为反应的催化因素，影响该组分的反应历程。其中，a、b、c代表调合组分，[a]代表a组分通过该途径产生的活性核，代表活性核通过一系列分支链反应生成的氢氧自由基。这一过程中，活性核一旦生成，就会迅速发生分支链反应产生大量氢氧自由基，后者迅速放热燃烧产生爆震，而各调合组分如何生成活性核是低温焰前反应的决速步骤，因此活性核转化率即是影响爆震的重要指标。

模型2b：

模型2b是由反应机理b建立的稳态方程推导而来的，稳态方程如以下2b’所示，tij是i组分和j组分的交互作用参数，ni、nj分别是i组分和j组分的摩尔分数,是体系新增的活性核转化率。

反应机理b

该模型认为在考察某一组分燃烧反应时，体系中的两组分间相互作用，促进体系中的活性核或惰性核生成，影响总活性核比重。其中，a、b、c代表调合组分，[m]代表该途径新产生的活性核，代表活性核通过一系列分支链反应生成的氢氧自由基。

模型3：辛烷值计算模型

根据爆震原理分析，认为活性核转化率与爆震强度正相关。而根据辛烷值标准，爆震强度与辛烷值负相关，因此活性核转化率与辛烷值负相关。据此可提出多种活性核转化率与辛烷值关系的模型猜想。本发明给出四种辛烷值计算模型，所述辛烷值计算模型选自以下四种中的一者：

模型3a(线性函数)：ron＝aqac+b

模型3b(倒数函数)：ron＝a/qac+b

模型3c(二次函数)：ron＝a(qac+b)²+c

模型3d(指数函数)：ron＝exp(aqac+b)

其中，ron是辛烷值，qac是活性核转化率，a、b、c是修正参数。建模中应调整这些参数保证辛烷值与活性核转化率负相关规律。

上述三种模型总结如下表：

最终，辛烷值预测模型的数学关系式可为这三部分模型的组合，组合方式为：

辛烷值＝模型3(模型1+模型2)

在组合时，模型1、2都是可选部分，也可以完全不考虑。当只考虑模型3并采用线性模型3a时，最终得到的辛烷值模型就是最简单的线性模型。当这样的预测模型用于单一组分时，公式左边的辛烷值即为该纯组分的辛烷值，用oni代替，右边的υi的值为1，此时可以消掉模型中的大多数未知参数，达到简化模型的目的。另外，在采用模型2对模型1中的活性核转化率加以修正时，可以将新增的活性核加在模型1的分子之上，或令：

将新增活性核的量折算为新增的i组分摩尔分数，此时：

ni＝(1+ii)ni或ni＝(1+imix/ni)ni

做以上处理后，再将修正后的i组分摩尔分数代入模型1中计算活性核转化率。

本发明可对上述三个模型进行分别建模以及多个模型猜想，并利用上述三个模型组合形成最终的辛烷值预测模型，期间可考虑根据纯烃辛烷值数据简化模型相关参数，确定模型中各参数的理论解释及初值。最终，可利用成品油数据，对辛烷值预测模型中参数进行校正，最终得到完整的基于详细组成的辛烷值预测模型。

下面给出通过本发明建立辛烷值预测模型数学表达式的三个实施例。

实施例一

对于组合的三个部分，分别选取模型1a、模型2a、模型3a，代入纯烃辛烷值，简化中间参数，得到基于汽油详细组成的辛烷值预测模型表达式1a-2a-3a:

其中,p代表考虑参与模型2活性核转化率修正的组分，其中，ρi是i组分的相对密度，mi是i组分的相对分子量。oni为各纯组分的辛烷值，是已知参数，υi是i组分体积分数，βi、a为模型需要回归的参数，其中，βi的初值可由i组分的密度和分子量求取。

通过这样组合得到的模型表达式与exxon公司通过实验得到的公式相似，但是通过本方法得到的公式各参数都具有实际意义，并给出了关键参数βi的初值获取办法：根据辛烷值测试方法可知，正庚烷和异辛烷的βi为1，且密度和分子量也已知，按照βi参数意义，插值得到其它组分βi初值。

利用我们获取的194个成品油样本及67个组分油样本数据验证，该数学表达式对辛烷值有较好的预测精度。如图3所示，横坐标为样本实际测量的辛烷值，纵坐标为通过模型计算得到的辛烷值,“*”为模型参数训练集，“+”为模型参数测试集，结果显示标准偏差为0.513。

实施例二

对于组合的三个部分，分别选取模型1a、模型2b、模型3a，代入纯烃辛烷值，简化中间参数，得到基于汽油详细组成的辛烷值预测模型表达式1a-2b-3a:

其中，imix＝∑ijtijninj，tij为需要考虑参与模型2活性核转化率修正的i组分和j组分的交互作用参数，由模型回归得到。

同样利用实施例一中的方法得到参数βi初值，利用数据回归参数，并验证该表达式的预测效果。如图4所示，横坐标为样本实际测量的辛烷值，纵坐标为通过模型计算得到的辛烷值,“*”为模型参数训练集，“+”为模型参数测试集，结果显示标准偏差为0.488。

实施例三

对于组合的三个部分，分别选取模型1a、模型2a、模型3b，代入纯烃辛烷值，简化中间参数，得到基于汽油详细组成的辛烷值预测模型表达式1a-2a-3b:

式中各参数与实施例一相同。

同样利用实施例一中的方法得到参数βi初值，利用数据回归参数，并验证该表达式的预测效果，如图5所示，横坐标为样本实际测量的辛烷值，纵坐标为通过模型计算得到的辛烷值,“*”为模型参数训练集，“+”为模型参数测试集，结果显示标准偏差为0.532。

实施例四

可分别选取模型1a及3a，当对于纯烃时，模型1a可表达为：

qac＝ki(1)

模型3a的左边可用i组分纯烃辛烷值oni代替，变为：

oni＝aqac+b(2)

将(1)式代入(2)式中，可建立纯烃辛烷值oni与ki的关系：

将模型1a和(3)式重新代入模型3a中，可以消掉模型中的大多数未知参数，达到简化模型的目的，最终的辛烷值模型为：

其中,oni为各纯组分的辛烷值作为已知参数，vi是i组分体积分数，βi为i组分的调合因子，是模型需要回归的参数。通过少量的组成与辛烷值事实数据对模型进行训练，得到βi参数，就可以通过汽油组成预测其辛烷值。

对于该模型1a及3a的组合，可进行以下两个实施例来验证其有效性。

实施例1)，利用194个成品油样本及67个组分油样本数据对模型进行验证，其中20个数据作为训练集，剩余数据作为验证集使用。利用数据对模型参数回归后，模型对样本的辛烷值有较好的预测精度。如图6a所示，横坐标为样本实际测量的辛烷值，纵坐标为通过模型计算得到的辛烷值,“*”为模型参数训练集，“+”为模型参数测试集，结果显示其标准偏差为0.663。

实施例2)，将模型用于6组重整组分油和7组催化裂化组分油的预测，模型参数采用上述实施例1)中回归得到的参数，模型对样本的辛烷值有较好的预测精度。如图6b所示，横坐标为样本实际测量的辛烷值，纵坐标为通过模型计算得到的辛烷值,“*”为模型参数训练集，“+”为模型参数测试集，结果显示其标准偏差为0.371。

实施例五

可分别选取模型1c及3a，两者相组合并经过数学计算，简化中间参数，得到最终的辛烷值预测表达模型为：

其中,ni是i组分在低温焰前反应阶段产生的自由基摩尔分数，ni是i组分摩尔分数，θi是低温焰前反应阶段i组分生成自由基的反应速率，oni为各纯组分的辛烷值作为已知参数。

对于该模型1c及3a的组合，可进行以下两个实施例来验证其有效性。

实施例1)，利用194个成品油样本及67个组分油样本数据对模型进行验证，其中40个数据作为训练集，剩余数据作为验证集使用。利用数据对模型参数回归后，模型对样本的辛烷值有较好的预测精度。如图7a所示，横坐标为样本实际测量的辛烷值，纵坐标为通过模型计算得到的辛烷值,“*”为模型参数训练集，“+”为模型参数测试集，结果显示其标准偏差为0.649。

实施例2)，将模型用于某炼厂的70个催化裂化组分油的预测，模型参数采用上述实施例1)中回归得到的参数，模型对样本的辛烷值有较好的预测精度。如图7b所示，横坐标为样本实际测量的辛烷值，纵坐标为通过模型计算得到的辛烷值,“*”为模型参数训练集，“+”为模型参数测试集，结果显示其标准偏差为0.412。

实施例六

可分别选取模型1b及3a，两者相组合并经过数学计算，简化中间参数，得到最终的辛烷值预测表达模型为：

其中,oni为各纯组分的辛烷值作为已知参数，ni是i组分摩尔分数，θi是低温焰前反应阶段i组分生成自由基的反应速率，为模型需要回归的参数。通过少量的组成与辛烷值事实数据对模型进行训练，得到θi参数，就可以通过汽油组成预测其辛烷值。

利用194个成品油样本及67个组分油样本数据验证，该数学表达式对辛烷值有较好的预测精度。如图8所示，横坐标为样本实际测量的辛烷值，纵坐标为通过模型计算得到的辛烷值,“*”为模型参数训练集，“+”为模型参数测试集，结果显示标准偏差为0.663。

实施例七

可分别选取模型1a及3b，两者相组合并经过数学计算，简化中间参数，得到最终的辛烷值预测表达模型为：

其中,oni为各纯组分的辛烷值作为已知参数，vi是i组分体积分数，βi为模型需要回归的参数。通过少量的组成与辛烷值事实数据对模型进行训练，得到参数βi的值，就可以通过汽油组成预测其辛烷值。

利用194个成品油样本及67个组分油样本数据验证，该数学表达式对辛烷值有较好的预测精度。如图9所示，横坐标为样本实际测量的辛烷值，纵坐标为通过模型计算得到的辛烷值,“*”为模型参数训练集，“+”为模型参数测试集，结果显示标准偏差为0.681。

相应的，本发明实施例还提供一种机器可读存储介质，该机器可读存储介质上存储有指令，该指令用于使得机器执行本申请上述预测汽油辛烷值的方法。

以上结合附图详细描述了本发明实施例的可选实施方式，但是，本发明实施例并不限于上述实施方式中的具体细节，在本发明实施例的技术构思范围内，可以对本发明实施例的技术方案进行多种简单变型，这些简单变型均属于本发明实施例的保护范围。

另外需要说明的是，在上述具体实施方式中所描述的各个具体技术特征，在不矛盾的情况下，可以通过任何合适的方式进行组合。为了避免不必要的重复，本发明实施例对各种可能的组合方式不再另行说明。

本领域技术人员可以理解实现上述实施例方法中的全部或部分步骤是可以通过程序来指令相关的硬件来完成，该程序存储在一个存储介质中，包括若干指令用以使得单片机、芯片或处理器(processor)执行本申请各个实施例所述方法的全部或部分步骤。而前述的存储介质包括：u盘、移动硬盘、只读存储器(rom，read-onlymemory)、随机存取存储器(ram，randomaccessmemory)、磁碟或者光盘等各种可以存储程序代码的介质。

此外，本发明实施例的各种不同的实施方式之间也可以进行任意组合，只要其不违背本发明实施例的思想，其同样应当视为本发明实施例所公开的内容。