一种大脑功能网络关键节点搜索方法与流程

本发明属于生物医学信息处理技术领域，具体地说，是一种大脑功能网络关键节点搜索方法，该方法基于组稀疏贝叶斯模型。

背景技术：

人类大脑是自然界存在的一种极具复杂的系统，各类神经元细胞通过突触连接在一起，形成了一个非常复杂的大脑结构网络，它是大脑进行各种生理和认知活动的结构基础。大脑在进行主动或由于外界刺激引起的被动活动过程中，各神经元或神经动态过程延伸为一个复杂的大脑功能网络，它是大脑神经活动变化的直观描述。可以看到，脑网络中的功能连接与结构连接密切相关，功能连接受到结构连接的限制，但也能通过结构连接来预测网络的功能连接。

目前人们利用静息态功能磁共振成像技术对大脑进行研究，与脑电图相比，功能磁共振数据拥有更好的空间分辨率，其空间分辨率可以达到毫米水平。作为一种非损伤性脑成像技术，磁共振成像在脑功能研究中发挥了不可替代的作用。静息态功能磁共振方法以其简单的实验设计，较高的信噪比，简单的数据处理流程而被广泛采用。

在自然界中，几乎每一个系统总有一个或者多个主要素占有非常重要的位置，因此由复杂网络抽象出来的复杂网络中的每个节点的重要程度是不同的，在各种复杂网络中，用定量分析的方法寻找复杂网络中的关键节点是复杂网络研究的一个基本问题。刻画节点重要程度的一个指标就是节点中心化指标，用于定量地表示一些节点比其他节点更重要的程度，该指标用于确定网络中个体所处位置与其在群体中的影响或号召力之间的关系。同样，在脑网络中找到关键的节点对于脑网络拓扑结构的研究有非常重要的价值。

目前已有许多关于脑网络的研究，将其看成一种复杂网络，具有小世界网络和无标度网络的特性，但绝大部分研究都集中于将大脑看成一个整体，研究的是整个大脑功能网络的特性，但脑网络是由一些功能子网络构成的，于是根据功能磁共振数据经过稀疏化来提取每个脑区的特征，为以后对特征研究进行后续操作做铺垫。

稀疏贝叶斯方法是一种通用的贝叶斯方法，通过定义先验分布的方法达到稀疏，相比于其他机器学习的稀疏方法如：lasso、spgl1等方法，稀疏贝叶斯的最大优势是它能得到最优解。为了不失一般性，利用线性模型去学习贝叶斯方法并用于搜索大脑功能网络关键节点，是一种实用的技术方法。

技术实现要素：

本发明针对现有技术存在的不足和实际应用的需要，披露了一种大脑功能网络关键节点搜索方法，所要解决的问题是：

提供一种基于组稀疏贝叶斯模型的大脑功能网络关键节点搜索方法，利用组贝叶斯稀疏模型将多层大脑功能网络的每一层网络进行稀疏并搜索出关键节点。关键节点能有效地体现出网络拓扑属性的重要性，在脑结构研究和脑疾病诊断等领域具有重要的应用价值。

为了达到上述目的，本发明采取以下技术方案：

一种大脑功能网络关键节点搜索方法，结合了组稀疏贝叶斯模型，包括以下步骤：

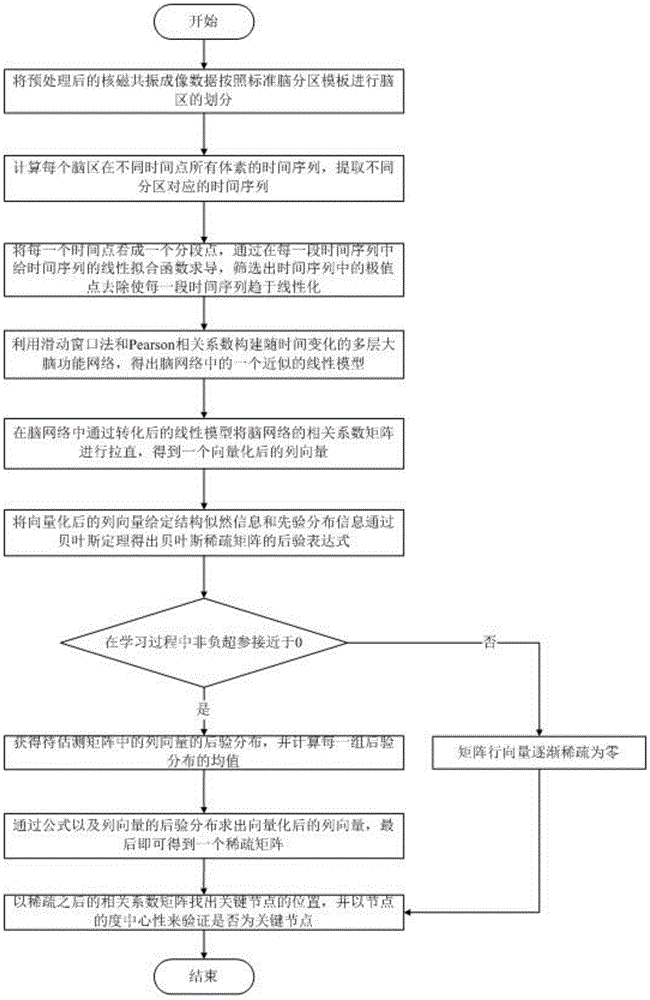
对采集的大脑功能磁共振成像进行格式转换和预处理，包括：时间校正、空间配准、标准化、滤波；选定一种标准化大脑分区模板将大脑划分为若干个脑区，每个脑区分别抽象为大脑功能网络中的一个节点；

(1)计算功能磁共振图像中每个脑区在不同时间点所有体素的平均时间序列，提取aal分区模板所对应的时间序列，设定时间序列x为x＝＜x1,x2,...,xn＞，分段点的集合为x′＝＜x1′,x2′,...,xm′＞；x的分段线性表示为：

xl＝(f1(x1,x2′),f2(x2′,x3′),...,fm-1(x′m-1,xm′))(1)

式中，fm-1(x′m-1,xm′)表示在段内区间[x′m-1,xm′]内的线性拟合函数；

(3)将每一个时间点看成一个分段点，在每一段时间序列中给时间序列的线性拟合函数求导，筛选出时间序列中的极值点并去除使每一段时间序列趋于线性化，由此得出整条时间序列近似趋于线性模型；

(4)用滑动时间窗法将处理之后的脑区全程时间序列分割成若干段；每一段相互重叠，窗口长度相同；计算每个时间子段的相关系数，构建基于每一段时间序列的大脑功能网络；滑动窗口法的表达式如下：

式中，时间窗口长度为l，窗口之间的间隔步长为s，每个脑区对应的总的时间序列长度为p，整个时间序列划分为l段；计算每个时间子段的相关性，构建随时间变化的动态大脑功能网络以保证网络构建随时间变化的灵活性；

(5)将多层脑网络的每层以行为单位分成n组，每一组参数描述了由一个节点发出的所有连边的情况，由于两变量之间的稀疏贝叶斯算法的基本分布为：

p(θi；γi)～n(0,γi),i＝1,...,n(3)

式中，所要求的是稀疏矢量θi，假设θi中每个向量都服从均值为0，方差为γi的正态分布，由此算法自动估算出θi的值；将稀疏贝叶斯算法应用到脑网络的相关系数矩阵中，设给定的相关系数矩阵记为s，则相关系数矩阵中的每一行为一个行向量si，.每一行给定一个零均值正态先验分布，具体表示为：

p(si，.；γi)～n(0,γiin),i＝1...n(4)

式中，in表示n×n的单位矩阵，γi是用于控制相关系数矩阵s第i行si稀疏性的非负超参；向量组在学习的过程中对超参γi进行估算，如果γi十分接近于零，相关系数矩阵中的行向量si会被强制变成零向量，即会被稀疏掉；如果γi并不接近于零，那么相关系数矩阵中的行向量就不会改变；向量γ＝[γ1,...,γn]^t是一个控制量，用于学习和保留关键节点，同时舍弃掉不重要的节点；

(6)引出通用的线性模型的表达式：

y＝xs+v(5)

式中，x为输入矩阵，y是目标矩阵，v为噪声矩阵；输入矩阵x和目标矩阵y都是从g∈r^n×n提取出来的有一样的规模；将通用模型转化为脑网络中的向量形式：

y＝xs+v(6)

式中，噪声向量v都是独立的，均服从均值为0，方差为λ的正态分布，其中目标向量y＝vec(y^t)∈r^tn×1，v＝vec(v^t)∈r^tn×1；

(7)利用vec(·)将一个矩阵按列进行合并，将所有列转化成一个列向量叫矩阵的拉直；对一般的线性矩阵方程：

a1xb1+a2xb2+...+apxbp＝c(7)

矩阵x∈c^m×n是矩阵方程的解的充分必要条件是为通常的线性方程组gx＝c的解，式中其中表示两个向量的克罗内克积；由此给出输入向量x的求法，把输入向量x表示为待估测向量s变化前包括n个组，每组的长度是n，变化之后为s＝vec(s^t)∈r^n2×1，相关矩阵s的行稀疏化结构就等价于向量化后的列向量s的组稀疏结构，只需求出列向量s即可达到稀疏脑网络g的目的，一组向量化后的列向量s的求法如下：

式中，φ(s)是稀疏约束项，λ是平衡参数，一般为正数；

(8)给定的相关矩阵s中一组向量化后的列向量为

s＝[s1,...,sd1,...,sdn-1+1,...,sdw]^t，则s中的非零元素也分布于列向量中，用脑网络内节点间的相关系数作为结构似然信息，似然函数为：

式中，λ是平衡参数，向量γ＝[γ1,...,γn]^t是一个控制量，用于学习和保留关键节点，同时舍弃掉不重要的节点，以γ为变量的到似然估计函数；

对似然函数对数得：

最终结果就是要最小化用似然函数得到模型的最大似然分布：

p(y|s；λ)～ny|s(xs,λi)(11)

式中，λ是平衡参数，x是输入向量，y是输出向量，s为矩阵的列向量形式，i为单位矩阵；

得出给定列向量s的先验分布表达式为：

式中，向量中元素的相关性通过方差∑s来体现，为先验均值；想要达到稀疏结果则组中大部分元素为0，可得先验分布p(s；γ)～ns(0,∑0)，∑0＝diag{γ1i1,...,γnin}；根据贝叶斯推测得出贝叶斯稀疏矩阵的后验表达式的计算公式以及表达式，表达式服从高斯分布：

均值和方差由如下公式确定：

∑s＝∑0-∑0x^t(λi+x∑0x^t)^-1x∑0(16)

参数估计由后验分布均值给出，通过均值以及公式(8)对s进行稀疏；

(9)随着列向量的稀疏，很多元素被稀疏成0；当γi＝0时，对应的∑0中第i个矩阵块被稀疏成0，一组向量被稀疏，同理一个网络中的所有组向量都被稀疏；由公式(8)得出每一组待测向量后合并每一组即为一个稀疏矩阵，从而达到稀疏矩阵提取关键节点所在行的目的；

(10)通过网络稀疏化找到脑网络的关键节点，关键节点所在的行不全为0，而没有关键节点的行则由于算法的一步步稀疏逐渐变为0，度中心性可以通过节点度来反映了网络中各节点的相对重要性，节点度较高的节点则是脑网络中的重要节点，稀疏之后以相关系数矩阵的度中心性为网络拓扑特征验证稀疏方法的可靠性。

本发明的有益效果：本发明有助于精确定位对网络连通性贡献较大的关键节点，在脑结构研究和脑疾病诊断等领域具有重要的应用价值。

附图说明

图1是本发明一种大脑功能网络关键节点搜索方法的实施流程图。

具体实施方式

为了加深对本发明的理解，下面将结合附图和实施例对本发明做进一步详细描述，该实施例仅用于解释本发明，并不对本发明的保护范围构成限定。

实施案例：一种大脑功能网络关键节点搜索方法的具体实施案例，包括以下步骤：

(1)选用正常组志愿者被试30例(男女各15人)采集大脑功能磁共振数据，测试前需要了解志愿者的身体状态，并且提醒被试者保持清醒的状态，不要有任何有意识的思维活动。使用philips3.0-teslascanner采集大脑功能磁共振数据，将读取到的磁共振图像数据利用dicom格式转换为nifti格式，再进行时间矫正、头动矫正、配准、空间标准化、平滑等预处理，最后进行低频滤波，降低低频漂移及高频的生物噪音。本实施例中，低频滤波范围取0.01hz～0.08hz。

(2)选定一种标准化大脑分区模板(如aal分区模板、brodmann分区模板、ch2分区模板等)将大脑划分为若干个脑区，每个脑区分别对应大脑功能网络中的一个节点。本实施例中，选取aal脑分区模板进行脑区的划分，将人脑划分为90个(左右半脑各45个)脑区，90个脑区对应大脑功能网络中的90个节点。记录核磁共振图像中每个脑区在不同时间点所有体素的时间序列，提取不同标准分区所对应的时间序列。

(3)如果时间序列x＝<x1,x2,...,xn>上的某点满足以下条件之一，则为时间序列中的某一极值点：

①xi＞xi-1且xi≥xi+1，或xi≥xi-1且xi＞xi+1，其中1＜i＜n；

②xi＜xi-1且xi≤xi+1，或xi≤xi-1且xi＜xi+1，其中1＜i＜n；

时间序列分段表示为：

xl＝(f1(x1′,x2′),f2(x2′,x3′),...,fm-1(xm′-1,xm′))(1)

式中，fm-1(x′m-1,xm′)表示为一个时间段内的线性拟合函数。运用pratt和fink提出的近似线性表示plr-ip方法，输入一整段时间序列之后输出趋于线性的时间序列。本实施例实现简单、保留了大部分局部特征以及降低噪音，由此得出的整条时间序列近似趋于线性模型。

(4)应用滑动时间窗法，将处理之后的脑区全程时间序列分割成若干段。每一段相互重叠，窗口长度相同。计算每个时间子段的相关系数，构建基于每一段时间序列的大脑动态功能网络。本实施例中，采用pearson相关系数。滑动窗口法的表达式如下：

式中，时间窗口长度为l，窗口之间的间隔步长为s，每个脑区对应的总的时间序列长度为p，整个时间序列被划分为l段。由此可以得到脑网络中关于时间节点的一个线性模型：

xt+1＝xt+ε,t∈[0,...,t](3)

式中，行向量表示在t时刻，包含n个节点的系统状态，为第i个节点在t时刻的系统状态，脑网络g∈r^n×n描述了脑中各节点的交互结构，ε是一个未知的噪声向量。

(5)通用的线性模型表达式为：

y＝xs+v(4)

式中，x为输入矩阵，y是目标矩阵，v为噪声矩阵，且x和y都是从g∈r^n×n中提取出来的矩阵，要求得稀疏表示待估测矩阵s矩阵则至关重要。对于目标矩阵的每一行yt,..＝xt+1,.，表示时刻t的系统状态和下一时刻t+1的时刻状态。输入矩阵x和目标矩阵y都从g∈r^n×n提取出来，规模相同，利用通用模型转化为脑网络中的向量形式：

y＝xs+v(5)

式中，噪声向量v都是独立的，均服从均值为0，方差为λ的正态分布其中y＝vec(y^t)∈r^tn×1，s＝vec(s^t)∈r^n2×1，v＝vec(v^t)∈r^tn×1，因为要对向量进行贝叶斯稀疏处理，所以利用vec(·)将一个矩阵按列进行合并，将所有列转化成一个列向量叫矩阵的拉直，拉直后的元素都是线性的；待估测向量s包括n个组，每组的长度也是n。对于输入向量x的求法，这里引用定理：对一般的线性矩阵方程，

a1xb1+a2xb2+...+apxbp＝c(6)

矩阵x∈c^m×n是矩阵方程的解的充分必要条件是为通常的线性方程组gx＝c的解，式中表示两个向量的克罗内克积。根据该定理，把输入向量x表示为相关矩阵s的行稀疏化结构就等价于向量化后的列向量s的组稀疏结构，只需求出列向量s即可达到稀疏脑网络g的目的。一组向量化后的列向量s的求法如下：

式中，φ(s)是稀疏约束项，λ是平衡参数向量，一般都为正数。

(6)给定的相关矩阵s中一组向量化后的列向量为s＝[s1,...,sd1,...,sdn-1+1,...,sdw]^t，则s中的非零元素也分布于列向量中，用脑网络内节点间的相关系数作为结构似然信息，似然函数为：

式中，λ是平衡参数，向量γ＝[γ1,...,γn]^t是一个控制量，用于学习和保留关键节点，同时舍弃掉不重要的节点，以γ为变量的到似然估计函数。

对似然函数对数得：

最终结果就是最小化可以得到模型的最大似然分布：

p(y|s；λ)～ny|s(xs,λi)(10)

式中，λ是平衡参数向量，x是输入向量，y是输出向量，s为矩阵的列向量形式；得出给定列向量s的先验分布表达式为：

式中，向量中元素的相关性通过∑s来体现，为先验均值。想要达到稀疏结果则组中大部分元素为0，可得先验分布p(s；γ)～ns(0,∑0)，∑0＝diag{γ1i1,...,γnin}。根据贝叶斯定理，可以得出贝叶斯稀疏矩阵的后验表达式的计算公式以及表达式：

二者有如下公式确定：

∑s＝∑0-∑0x^t(λi+x∑0x^t)^-1x∑0(15)

参数估计由后验分布均值μs给出，通过均值以及公式(7)对s进行稀疏；

(7)随着列向量的稀疏，很多元素被稀疏成0。当γi＝0时，对应的∑0中第i个矩阵块被稀疏成0，从而一组向量被稀疏，同理一个网络中的所有组向量都被稀疏，由公式(7)得出每一组待测向量后合并每一组即为一个稀疏矩阵，从而达到稀疏矩阵提取关键节点所在行的目的。网络稀疏化的作用是为了找到一组脑网络的关键节点，因为只有关键节点所在的行不全为0，而没有关键节点的行则由于算法的一步步稀疏逐渐变为0。以稀疏之后的相关系数矩阵的度中心性为网络特征，找出关键节点的位置。

(8)关键节点所在的行不全为0，而没有关键节点的行则由于算法的一步步稀疏逐渐变为0，利用网络拓扑结构中的度中心性来检验。度中心性可以通过节点度来反映了网络中各节点的相对重要性，节点度较高的节点在很大概率上是脑网络中的重要节点，所以利用节点度的大小来验证稀疏之后搜索出来的节点是否为关键节点，其计算公式如下所示：

式中，n为节点的总数，kij是节点之间的边数。本实施例中，通过matlab软件编程计算网络中的各节点的节点度，观察比较得出网络中稀疏化后搜索出的节点节点度大，相应验证了此类节点是关键节点。搜索出关键节点有助于定位对网络连通性贡献较大的点，为以后的脑结构和脑疾病诊断等研究提供了理论依据。

以上显示和描述了本发明的基本原理、主要特征及优点。本行业的技术人员应该了解，本发明不受上述实施例的限制，上述实施例和说明书中描述的只是说明本发明的原理，在不脱离本发明精神和范围的前提下，本发明还会有各种变化和改进，这些变化和改进都落入要求保护的本发明范围内。本发明要求保护范围由所附的权利要求书及其等效物界定。