一种微管-驱动蛋白输运系统的行走动力学计算方法与流程

本发明涉及蛋白质机器动力学领域，具体涉及一种微管-驱动蛋白输运系统的行走动力学计算方法。

背景技术：

微管-驱动蛋白输运系统是囊泡运输和细胞分裂等一系列生命活动的重要组成部分。研究微管-驱动蛋白输运系统的行走动力学行为，有助于明确微管与驱动蛋白间相互作用的力学机理，深入理解分子转运系统的运动机制，并进一步推动仿生纳米机械的设计与合成。

在驱动蛋白行走过程中，颈链与微管的结合状态包含一个头部结合和两个头部结合的切换，并且行走过程会造成驱动蛋白空间位置变化。当驱动蛋白只有一个头部结合微管时(即单头结合阶段)，驱动蛋白有且仅有一个头部连接在微管上，所有外力都经由茎部，通过单根颈链与微管的约束传递给微管结构，另外一个颈链内部则没有力的传递；当驱动蛋白两个头部都结合微管时(即双头结合阶段)，驱动蛋白的两个头部分别与微管结合，外力都经由茎部，通过两根颈链从不同的接触约束点传递给微管结构。两个阶段驱动蛋白的空间位置不同，与微管的约束条件不同，其各自的停留时间也不相同，因此研究驱动蛋白行走过程中微管-驱动蛋白输运系统的动力学，需要对两个阶段的系统响应分别求解。

目前已有的理论研究，大多是对微管结构和驱动蛋白结构力学行为的单独求解，忽略了两个结构之间的相互作用，也难以计算微管-驱动蛋白整个输运系统受到外部扰动时的动力响应。少部分的对于微管-驱动蛋白输运系统的研究中，系统的物理模型极端简化，忽略了微管结构内部二聚体纵向与横向相互作用的差异，也没有考虑驱动蛋白行走过程中空间结构的不同以及与微管间约束条件的改变，这样求得的系统响应不仅难以与实际输运状况相吻合，对于仿生机械的研究也没有足够的借鉴意义。

技术实现要素：

本发明的目的在于提供一种微管-驱动蛋白输运系统的行走动力学计算方法，不仅可以求解驱动蛋白在微管上行走的耦合振动，还可以获得货物受流体环境作用时输运系统的瞬态动力响应。

实现本发明目的的技术解决方案为：一种微管-驱动蛋白输运系统的行走动力学计算方法，具体包括以下步骤：

步骤1：基于分子势能与结构应变能等效的原理获得微管驱动蛋白输运系统的物理参数，建立微管-驱动蛋白输运系统几何模型；

步骤2：对微管-驱动蛋白输运系统几何模型的惯性场和变形场进行有限元离散，结合第二类lagrange方程获得驱动蛋白结构和微管结构各自的动力学方程；

步骤3：根据不同结合阶段的不同约束条件，合并驱动蛋白结构的动力学方程和微管结构的动力学方程，删除多余自由度，构建微管-驱动蛋白输运系统的动力学方程；

步骤4：使用newmark法对微管-驱动蛋白输运系统动力学方程直接积分，求解微管-驱动蛋白输运系统在驱动蛋白行走过程中的瞬态动力学响应。

本发明与现有技术相比，其显著优点在于：

(1)本发明考虑了驱动蛋白不同结构域的力学性能差异，以及微管结构内部二聚体纵向与横向的不同相互作用，其中的各项物理参数基于单分子实验数据等效获得，使得模型更能反应纳米结构的尺度效应；

(2)本发明考虑了驱动蛋白行走过程中空间结构和空间位置的差异，区分了驱动蛋白与微管不同结合阶段的动力学方程，使微管-驱动蛋白输运系统行走动力学的求解更加精细和准确；

(3)本发明考虑到输运系统运行的实际环境，可以求解运输货物受到外部扰动情况下系统的瞬态响应，填补了受扰动输运系统动力学研究的理论空缺，使计算方法可以更广泛、灵活地应用到纳米机器行走动力学的研究当中。

附图说明

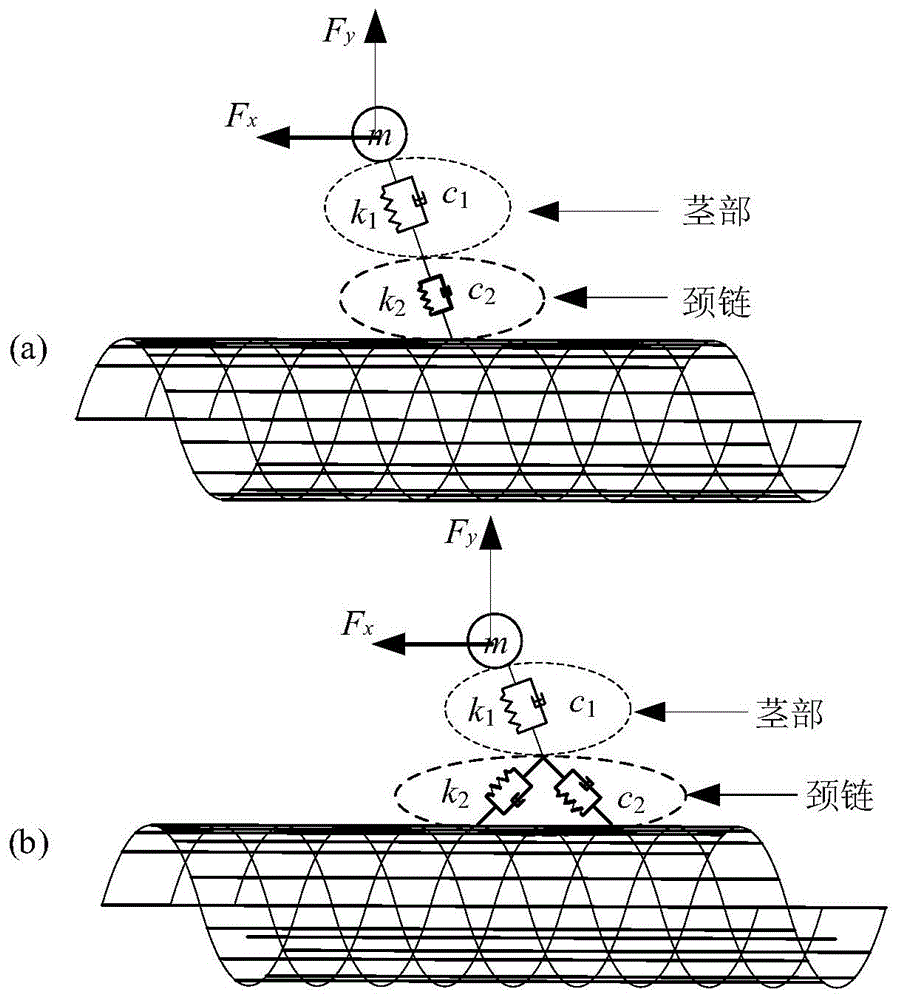
图1为微管-驱动蛋白输运系统的几何模型，其中图(a)驱动蛋白与微管单头结合阶段的模型图，图(b)为驱动蛋白与微管双头结合阶段的模型图。

图2为单头结合阶段驱动蛋白结构的物理模型和离散后的有限元模型图，其中图(a)为物理模型图，图(b)为有限元模型图。

图3为双头结合阶段驱动蛋白结构的物理模型和离散后的有限元模型图，其中图(a)为物理模型图，图(b)为有限元模型图。

图4为微管网络模型细节示意图。

图5为基于newmark法的积分求解流程图。

图6为路径原纤维上不同节点处垂直位移与时间的曲线图。

图7为本发明微管-驱动蛋白输运系统的行走动力学计算方法流程图。

具体实施方式

下面结合附图对本发明作进一步详细描述。

结合图7，一种微管-驱动蛋白输运系统的行走动力学计算方法，具体包括以下步骤：

步骤1：基于分子势能与结构应变能等效的原理获得微管驱动蛋白输运系统的物理参数，建立微管-驱动蛋白输运系统几何模型如图1所示。

微管-驱动蛋白输运系统包括微管结构和驱动蛋白结构，微管是由αβ-二聚体排列构成的网状结构，微管纵向由多根原纤维平行围绕而成，微管横向为有固定起始数的螺旋结构，驱动蛋白包括依次连接的头部、颈链、茎部和尾部结构。

微管-驱动蛋白输运系统的物理参数包括微管的物理参数和驱动蛋白的物理参数，其中微管的物理参数包括微管纵向圆截面梁单元的截面直径d1、截面积a1、弹性模量e1、截面惯性矩i1、长度l、密度ρ1，以及微管横向圆截面梁单元的截面直径d2、截面积a2、弹性模量e2、截面惯性矩i2、螺旋起始数s和螺旋圈数n0、密度ρ2，驱动蛋白的物理参数包括茎部弹簧刚度kc、长度l1，颈链弹簧刚度kn、长度l2。微管圆截面梁单元的拉伸刚度ea、弯曲刚度ei和扭转刚度gj基于计算化学中分子势能与结构力学中应变能之间的能量等效确定，再根据截面积公式a＝πd²/4，截面惯性矩公式i＝πd⁴/64和截面极惯性矩公式j＝πd⁴/32，得到纵向梁和横向梁的截面直径及弹性模量的具体参数。驱动蛋白茎部和颈链的弹簧刚度从分子力学模拟中对驱动蛋白弹簧拉伸试验获得。

当驱动蛋白尾部连接的货物受到细胞基质环境粘性力的影响时，整个微管-驱动蛋白输运系统将在蛋白尾部和货物连接点受到与前进方向相反的水平阻力fx和竖直方向负载力fy的作用，驱动蛋白茎部被外力拉伸使得驱动蛋白茎部与竖直方向产生相应的夹角，由此建立微管-驱动蛋白输运系统几何模型。微管-驱动蛋白输运系统在驱动蛋白行走过程中的几何模型分为两个结合阶段：当驱动蛋白只有一个头部结合微管时，有且仅有一根颈链连接微管与茎部，颈链与茎部沿着合力方向拉伸(如图1(a)所示)；当驱动蛋白两个头部都结合微管时，两根颈链分别与微管连接，茎部沿着合力方向拉伸，两根颈链在绞结点受到茎部轴力的作用(如图1(b)所示)。

步骤2：对微管-驱动蛋白输运系统几何模型的惯性场和变形场进行有限元离散，结合第二类lagrange方程获得驱动蛋白结构和微管结构各自的动力学方程。

当尾部承受货物负载的驱动蛋白仅有一个头部与微管结合时(即单头结合阶段)，如图2(a)所示，驱动蛋白仅有一根颈链连接微管与茎部，颈链与茎部沿着合力方向拉伸，其离散后的有限元模型如图2(b)。其中，茎部弹簧刚度为k1，阻尼为c1；颈链弹簧刚度为k2，阻尼为c2。

由单头结合阶段驱动蛋白结构内部阻尼力做的虚功变分，得到单头结合阶段驱动蛋白结构的广义力：

其中，v1、v2分别为茎部和颈链弹簧的轴向速度，δ(δl1)、δ(δl2)分别为茎部和颈链弹簧的位移变分，i表示节点位置，i＝1，2，3，(xi，yi，zi)为节点坐标，fi为xi方向的广义力，fi为yi方向的广义力，zi方向广义力为零。

将单头结合阶段驱动蛋白结构的广义力代入第二类lagrange方程：

其中，t1、v1分别为单头结合阶段驱动蛋白结构的动能和势能。

得到单头结合阶段驱动蛋白结构的有限元方程：

其中，m1、c1、k1分别表示单头结合阶段驱动蛋白结构的质量、阻尼和刚度矩阵，u1、f1分别表示单头结合阶段驱动蛋白结构的位移向量和荷载向量。

当尾部承受货物负载的驱动蛋白两个头部分别与微管结合时(即双头结合阶段)，如图3(a)所示，驱动蛋白两根颈链分别与微管连接，茎部沿着合力方向拉伸，两根颈链在绞结点受到茎部轴力的作用，其离散后的有限元模型如图3(b)所示。

由双头结合阶段驱动蛋白结构内部阻尼力做的虚功变分，得到双头结合阶段驱动蛋白结构的广义力：

其中，v1、v2、v3分别为茎部和两根颈链弹簧的轴向速度，δ(δl1)、δ(δl2)、δ(δl3)分别为对应的茎部和两根颈链弹簧的位移变分，j表示节点位置，j＝1，2，3，4，(xj，yj，zj)为节点坐标，fj为xj方向的广义力，fj为yj方向的广义力，zj方向广义力为零。

将双头结合阶段驱动蛋白结构的广义力代入第二类lagrange方程：

其中，t2、v2分别为双头结合阶段驱动蛋白结构的动能和势能。

得到双头结合阶段驱动蛋白结构的有限元方程：

其中，m2、c2、k2分别表示双头结合阶段驱动蛋白结构的质量、阻尼和刚度矩阵，u2、f2分别表示双头结合阶段驱动蛋白结构的位移向量和荷载向量。

为了区分微管纵向αβ-二聚体的强烈相互作用和微管横向二聚体间较弱的相互作用，定义微管纵向梁单元和横向梁单元如图4所示，使用空间梁单元对微管结构进行网格剖分，得到微管结构的动力学方程如下：

其中，微管结构的质量矩阵m0、阻尼矩阵c0、刚度矩阵k0、位移矩阵u0和载荷矩阵f0的具体表达式如下：

其中，m^ekl为微管质量子矩阵，k^ekl为微管刚度子矩阵，ak为微管位移子矩阵，pk为微管载荷子矩阵。空间梁单元每个节点有6个自由度，即有6个广义位移和6个广义力，则微管各个子矩阵的具体表达式为：

步骤3：根据不同结合阶段的不同约束条件，合并驱动蛋白结构的动力学方程和微管结构的动力学方程，删除多余自由度，构建微管-驱动蛋白输运系统的动力学方程，具体如下：

合并单头结合阶段驱动蛋白结构的动力学方程和微管结构的动力学方程：

其中，和分别表示单头结合阶段驱动蛋白结构和微管结构的合并质量、阻尼和刚度矩阵，和分别表示单头结合阶段驱动蛋白结构和微管结构的合并位移和荷载向量，具体表达式如下：

当驱动蛋白单个头部与微管结合时，驱动蛋白结构与微管结构间的约束条件为头部结合节点nh和微管结合节点nb具有相同的位移、速度和加速度，头部结合节点nh的坐标为(xh，yh，zh)，微管结合节点nb的坐标为(ub，vb，wb)，定义约束条件：

利用约束条件删除多余自由度，得到仅包含独立坐标的单头结合阶段微管-驱动蛋白输运系统动力学方程：

其中，m11、c11和k11分别为去除多余自由度后单头结合阶段微管-驱动蛋白输运系统的全局质量、阻尼和刚度矩阵，u11和f11分别为去除多余自由度后单头结合阶段微管-驱动蛋白输运系统的全局位移和荷载向量。

合并双头结合阶段驱动蛋白结构的动力学方程和微管结构的动力学方程：

其中，和分别表示双头结合阶段驱动蛋白结构和微管结构的合并质量、阻尼和刚度矩阵，和分别表示双头结合阶段驱动蛋白结构和微管结构的合并位移和荷载向量。具体表达式如下

当驱动蛋白两个头部分别与微管结合时，驱动蛋白结构的领先头部结合节点nh1与微管结构的结合节点nb1具有相同的位移、速度和加速度，驱动蛋白结构的落后头部结合节点nh2与微管结构的结合节点nb2具有相同的位移、速度和加速度，领先头部结合节点nh1的坐标为(xh1，yh1，zh1)，落后头部结合节点nh2的坐标为(xh2，yh2，zh2)微管结合节点nb1的坐标为(ub1，vb1，wb1)，nb2的坐标为(ub2，vb2，wb2)，定义约束条件：

利用约束条件删除多余自由度，可得仅包含独立坐标的双头结合阶段微管-驱动蛋白输运系统动力学方程：

其中，m22，c22和k22分别为去除多余自由度后双头结合阶段微管-驱动蛋白输运系统的全局质量、阻尼和刚度矩阵，u22和f22分别为去除多余自由度后双头结合阶段微管-驱动蛋白输运系统的全局位移和荷载向量。

步骤4：使用newmark法对微管-驱动蛋白输运系统动力学方程直接积分，求解微管-驱动蛋白输运系统在驱动蛋白行走过程中的瞬态动力学响应，积分求解流程图如图5所示。

基于步骤3中两个结合阶段分别对应的输运系统的动力学方程，将求解的连续时间区间划分为一系列的离散时间点，各离散时间点间隔δt＝tr+1-tr为积分时间步长，r＝0，1，2，3…，设tr时刻微管-驱动蛋白输运系统的运动位移ur、速度和加速度均已求得，newmark法假定tr～tr+1时段内系统的加速度值为介于和间的某个值，引入两组控制参数δ和α以及振幅衰减系数γ，令γ≥0，当δ＝1/2+γ且α≥(1+γ)²/4时，newmark法将无条件稳定，此时设加速度为：

在tr～tr+1的时间段上对加速度积分，得tr+1时刻的速度和位移：

将公式(22)代入(21)，得到：

推得tr+1时刻系统运动加速度和速度的计算公式：

其中，第一系数a0＝1/(αδt²)，第二系数a1＝δ/(αδt)，第三系数a2＝1/(αδt)，第四系数a3＝1/(2α)-1，第五系数a4＝δ/α-1，第六系数a5＝(δ/α-2)δt/2。代入tr+1时刻的运动方程：

得到tr+1时刻的输运系统的位移ur+1、速度ur+1和加速度其中，m、c和k分别为微管-驱动蛋白输运系统的全局质量、阻尼和刚度矩阵，u为微管-驱动蛋白输运系统的全局位移向量，fr+1为tr+1时刻微管-驱动蛋白输运系统的荷载向量，单头结合阶段有m＝m11、k＝k11、c＝c11、u＝u11、双头结合阶段有m＝m22、k＝k22、c＝c22、u＝u22、

本发明区分了驱动蛋白行走过程中与微管不同结合阶段空间结构和空间位置的差异，能够更加准确地求解运输货物受到外部扰动情况下微管-驱动蛋白输运系统的动力学响应，对细胞活动中输运系统的动力学研究有重要帮助，还可以应用到纳米机器的设计和研发当中。

实施例

本发明实施的案例提供了一种微管-驱动蛋白输运系统的行走动力学计算方法，求解了货物受流体环境作用时，输运系统在驱动蛋白行走过程中的瞬态动力响应。令驱动蛋白尾部受到6pn的外载荷，以200nm/s的速度沿着微管原纤维步行走了128nm，外载荷方向与路径原纤维夹角为60°，即尾部受到与前进方向相反的水平阻力fx＝3pn，竖直方向负载力fy＝5.2pn，茎部与颈链绞结点距离路径原纤维的高度为1.5nm。每个单头结合阶段对应时间为0.0533s，双头结合阶段对应时间为0.0267s，积分时间步长为0.0001s。

具体求解步骤如下：

步骤1：基于分子势能与结构应变能等效的原理获得系统的物理参数，建立微管-驱动蛋白输运系统的几何模型。构建纵向梁长度l＝200nm，横向梁螺旋起始数s＝3和螺旋圈数n0＝16的微管模型，其中纵向圆截面梁单元的截面直径d1、截面积a1、弹性模量e1、截面惯性矩i1、密度ρ1，以及微管横向圆截面梁单元的截面直径d2、截面积a2、弹性模量e2、截面惯性矩i2、密度ρ2如表1所示。

表1微管原丝和螺旋线方向梁单元的特征参数

另外驱动蛋白的茎部弹簧刚度kc和颈链弹簧刚度kn见表2。

表2驱动蛋白和微管模型的特征参数

步骤2：对模型的惯性场和变形场进行有限元离散，结合第二类lagrange方程获得驱动蛋白和微管子结构的动力学方程；

步骤3：根据不同结合阶段的不同约束条件，合并两个子结构并删除多余自由度，构建整体系统的动力学方程；

步骤4：使用newmark法对系统动力学方程直接积分，求解输运系统在驱动蛋白行走过程中的瞬态动力学响应。

在获得瞬态响应后，使用origin软件绘制瞬态响应的曲线，以驱动蛋白作为路径行走的微管原纤维上坐标为z＝20、50、100、150和180nm的五个节点为例，得到它们在整个运动过程中垂直位移随时间的响应如图6所示。观察同一节点不同时刻的节点垂直位移，可以发现驱动蛋白单头结合阶段和双头结合阶段微管的振动响应有明显的不同；观察不同节点的振动曲线，可以对驱动蛋白行走过程中蛋白空间位置变化导致的微管动力学响应展开分析。