一种基于土壤传递函数的目标土壤性质含量预测方法与流程

本发明涉及一种基于土壤传递函数的目标土壤性质含量预测方法，属于计量土壤技术领域。

背景技术：

作为人类生存环境的重要载体，社会经济的发展与土壤存在着紧密的联系。自20世纪以来，全球工业化的快速发展导致了土壤重金属含量的急剧增加，尤其工业区与各种矿区周边土壤的重金属含量非常高，已经严重影响到生态系统的稳定，引起了世界各国相关部门、广大人民的重视，是全球公认的热点话题。可持续生态农业的发展建议使用更为生态、环保的有机肥料。但是在当前农业生产中广泛施用的牛粪和猪粪会在土壤中产生糖类、酚类、有机酸等化合物，易导致土壤铜的螯合或络合，带来潜在的环境污染。土壤中的磷元素是植物生长所必需的三大主要营养元素之一。然而，据相关资料统计，我国大多数的农业生态系统的土壤磷含量低于植物的需求量，这也导致了我国近三十年来磷肥的使用量逐年上升。不合理的过量施用磷肥直接导致了土壤中大量的磷酸盐累积，显著影响了施用磷肥的当季利用率(约10％-20％)，造成了磷肥资源的损失与浪费。农田土壤中磷元素的大量累积也直接造成了严重的环境问题，主要体现在磷随水体迁移而造成的水体富营养化。因此，对土壤性质含量进行定期监测意义重大。

不同应用部门所创建的土壤数据库一般只是涉及到基本的土壤物理、化学性质，鲜有涉及到土壤微量元素含量、重金属含量数据，例如瓦赫宁根大学创建的wosis土壤数据库与联合国粮农组织创建的hwsd(harmonizedworldsoildatabasev1.2)数据库只是包含了土壤有机质、ph、质地、氮、磷、钾等基本的理化性质。

国内外相关技术部门、公司与学者已提出一系列的土壤性质含量化学测定方法。例如，可用的土壤有效铜含量测量方法包括：原子吸收光谱仪、dtpa-tea浸提法与原子吸收分光光度计等；可用的土壤全磷含量测量方法包括：高温烧灼酸浸提法、强酸消煮法、碱熔法、连续流动分析仪等。常规获取土壤性质含量信息的方法是野外样品采集和室内化学分析测试，该方法精度高，但费时费力，且难以获得区域土壤性质含量的空间分布信息。近年来有学者尝试使用室内反射光谱可见光/近红外光谱等技术来反演部分土壤性质含量。土壤中的铁氧化物、有机质对土壤重金属有一定的吸附作用，且在光谱曲线上体现一定的吸收特征，进而可以间接地预测土壤重金属含量。基于土壤元素对于光谱的响应特征，还可以构建土壤全磷与不同光谱指标的预测模型(例如偏最小二乘回归)。这一类方法具有高效、无损、快速等显著优点，在土壤成分快速检测中的应用潜力较大。但该方法在具体应用中存在一定的测量误差，不同研究区、不同操作人员的测定误差相差非常大。

然而，不同的土壤调查相关部门在实际中的需求各异，限于预算支出，这些部门不可能测定所有的土壤理化指标，只会测定与具体需求相关的一些土壤理化性质，例如土壤微生物调查、工程土壤调查。因此，部分的土壤调查虽然收集了不少的土壤样品，但后续的化学分析没有测定土壤重金属含量。由于历史土壤数据库的土壤样品大多数已经丢失，无法通过化学实验弥补缺失的土壤养分数据(例如土壤的氮磷钾含量)。当农业、生态相关的部门集成了多源的土壤数据进行土壤质量、肥力评价时，经常发现土壤数据库中不少的土壤样点数据缺少土壤有效钾含量的信息。

针对类似的数据库缺少数据的问题，技术人员提出使用土壤传递函数(ptf)来弥补缺失的土壤数据。土壤传递函数的原理是基于土壤物理、化学性质间的相关性，通过构建已测定土壤性质与未测定土壤性质的预测模型，来实现缺失数据的更新。常用的土壤传递函数模型主要包括统计回归模型、人工神经网络、物理经验模型等。其中，统计回归模型是应用部门经常采用的研究模型，在具体应用中存在容易实现、预测精度高、变量解释程度高等优点。

随着传感器技术、地理信息系统、全球定位系统等技术的飞速发展，地理、地质、气象、遥感、土地规划等部门生产制作了大量的环境要素图层，例如土壤温度、蒸散发、年平均降水量、年平均气温、年平均日照、湿润指数、土地利用、高程、坡向等图层。从土壤演化的角度出发，土壤的演化受到了多种成土要素的综合作用：气候、地形、母质、生物和时间，可以使用成土要素变量来模拟预测土壤理化性质的空间变异特征，即土壤-景观模型。该技术在数字土壤制图领域已取得较为广泛的应用。

目前，基于土壤传递函数预测土壤性质含量，在预测技术与评估技术上存在一定的局限性，具体包括：

(1)通过对相关技术文献、专利与技术报告的检索，发现土壤传递函数预测土壤性质含量的技术较为匮乏。这主要是由于部分土壤性质含量与其他土壤其他理化性质相关性较低造成的。传统的土壤传递函数的构建也较少考虑不同尺度、地理范围全覆盖的环境变量的集成。尤其是当土壤理化性质间的相关性较低时，土壤传递函数的构建需要大量的土壤数据的支持，数据量的大小直接影响到了预测模型的精度。欠缺对环境变量的集成一定程度上影响了土壤传递函数在土壤性质含量预测的精度。

(2)数理统计模型在实际应用中需要考虑的一个重要因素就是不确定性。不确定性也是土壤传递函数在实际应用中较为欠缺的一个要素。例如基于最小二乘法的土壤传递函数，必须厘定各输入要素(土壤理化性质)的误差，才能通过相关预测模型评估该线性模型涉及到的不确定性传播。

(3)获取到的土壤传递函数仅能预测样点尺度的土壤信息，无法扩展到区域尺度，形成能够服务于更多应用部门的土壤图。由于传统的土壤传递函数的输入数据是实验室分析的土壤理化性质数据，所构建的函数仅代表了测定的土壤性质含量与其他理化性质数据间的关系。覆盖区域的土壤图的精度是无法达到实验室分析的精度，因此无法直接将这些土壤传递函数直接应用在历史土壤图上进行土壤性质含量空间分布图的制作。

以上所述现有土壤性质含量预测技术的不足，已影响到生物、农学和环境等相关应用部门生产、加工土壤信息产品的具体效益，一定程度上给国家生态规划、精细农业部署造成了经济损失。

技术实现要素：

本发明所要解决的技术问题是提供一种基于土壤传递函数的目标土壤性质含量预测方法，采用全新设计架构，弥补了现有技术的不足，能够高效实现目标土壤性质含量的准确预测，提高工作效率。

本发明为了解决上述技术问题采用以下技术方案：本发明设计了一种基于土壤传递函数的目标土壤性质含量预测方法，用于实现目标区域中目标土壤性质含量的预测，包括如下步骤：

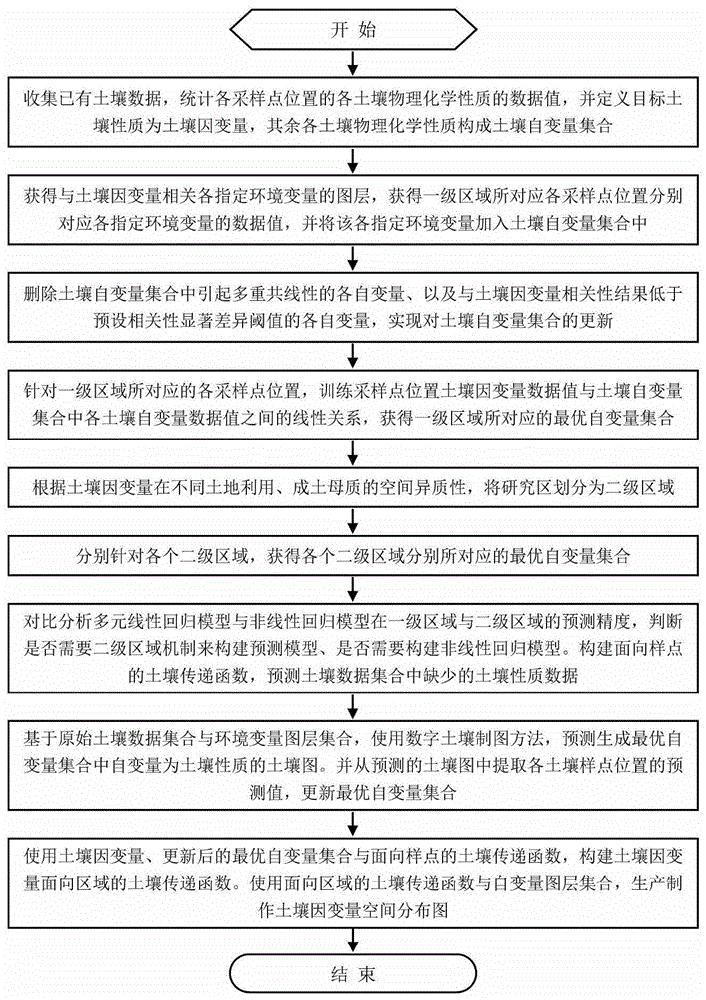
步骤a.基于已有土壤数据，选择目标区域中满足对应预设各土壤物理化学性质的数据值均为非空要求的各个采样点位置，并以该各采样点位置的最小外接多边形，构成一级区域，且该各采样点位置作为一级区域所对应的各采样点位置，预设各土壤物理化学性质中包含目标土壤性质，定义目标土壤性质为土壤因变量，除目标土壤性质以外的各土壤物理化学性质构成土壤自变量集合，然后进入步骤b；

步骤b.获得覆盖一级区域、与土壤因变量相关各指定环境变量的图层，分别针对一级区域所对应的各采样点位置，提取采样点位置所对应各指定环境变量的数据值，并将该各指定环境变量加入土壤自变量集合中，实现对土壤自变量集合的更新,然后进入步骤c；

步骤c.删除土壤自变量集合中引起多重共线性的各自变量、以及与土壤因变量相关性结果低于预设相关性显著差异阈值的各自变量，实现对土壤自变量集合的更新，然后进入步骤d；

步骤d.针对一级区域所对应的各采样点位置，采用逐步多元线性回归模型，基于预设迭代次数，训练采样点位置土壤因变量数据值与土壤自变量集合中各土壤自变量数据值之间的线性关系，分别获取每次迭代训练中所筛选的临时最优自变量集合，并统计不同临时最优自变量集合分别被选中的次数；待完成预设迭代次数的训练后，将被选中次数最高的临时最优自变量集合作为一级区域所对应的最优自变量集合，并进入步骤e；

步骤e.获得覆盖一级区域的预设属性土壤区域的划分图层，并针对一级区域所对应的各采样点位置，提取该各采样点位置分别所在该预设属性下的土壤划分区域，基于该各采样点位置的土壤因变量的数据值，分析获得该不同土壤划分区域之间对应土壤因变量的差异性结果，若该各差异性结果均不大于预设显著差异阈值，则进入步骤g；若该各差异性结果中存在大于预设显著差异阈值的差异性结果，则针对其中差异性结果不大于预设显著差异阈值的不同土壤划分区域进行合并，并结合未合并的各土壤划分区域，构成各个二级区域，以及基于一级区域所对应的各采样点位置，获得各个二级区域分别所对应的各采样点位置，然后进入步骤f；

步骤f.分别针对各个二级区域，采用步骤d的方法，获得各个二级区域分别所对应的最优自变量集合，并进入步骤g；

步骤g.针对一级区域所对应的各采样点位置，训练土壤因变量数据值与对应最优自变量集合中各自变量数据值之间的线性回归模型、非线性回归模型，并获得该线性回归模型的确定系数、以及非线性回归模型的确定系数，即一级区域所对应的线性回归模型确定系数r_ols、以及非线性回归模型确定系数r_nls；

进一步若不存在二级区域，则直接进入步骤h；若存在二级区域，则分别针对各个二级区域，训练对应各采样点位置土壤因变量数据值与对应最优自变量集合中各自变量数据值之间的线性回归模型、非线性回归模型，并获得该线性回归模型的确定系数、以及非线性回归模型的确定系数，进而获得各二级区域分别所对应的线性回归模型确定系数、以及非线性回归模型确定系数，并进一步获得所有二级区域所对应的线性回归模型确定系数的均值r_ols_mean、以及非线性回归模型确定系数的均值r_nls_mean；然后进入步骤h；

步骤h.若不存在二级区域，则进入步骤i；

若存在二级区域，当r_ols均大于r_ols_mean、r_nls_mean，或者r_nls均大于r_ols_mean、r_nls_mean，则进入步骤i；

当r_ols_mean均大于r_ols、r_nls，或者r_nls_mean均大于r_ols、r_nls，则进入步骤m；

步骤i.基于一级区域所对应的各个采样点位置、以及所对应的最优自变量集合，根据该各采样点位置分别对应该最优自变量集合中各土壤物理化学性质的数据值，获得该最优自变量集合中各土壤物理化学性质分别基于步骤b中全部指定环境变量的预测模型；然后结合步骤b中各指定环境变量图层，获得该最优自变量集合中各土壤物理化学性质分别对应一级区域的空间分布预测图层，然后进入步骤j；

步骤j.将一级区域所对应最优自变量集合中各土壤物理化学性质的空间分布预测图层、与该最优自变量集合中各环境变量对应一级区域的图层进行合并，构成一级区域所对应最优自变量图层集合，然后进入步骤k；

步骤k.若r_ols≥r_nls，则针对一级区域所对应的各采样点位置，由一级区域所对应最优自变量图层集合中提取各自变量数据值，并训练其与土壤因变量数据值之间的线性回归模型，构成一级区域预测模型，并进入步骤l；

若r_nls>r_ols，则针对一级区域所对应的各采样点位置，由一级区域所对应最优自变量图层集合中提取各自变量数据值，并训练其与土壤因变量数据值之间的非线性回归模型，构成一级区域预测模型，并进入步骤l；

步骤l.根据一级区域所对应最优自变量图层集合，应用一级区域预测模型，获得土壤因变量空间分布图，即目标区域中目标土壤性质空间分布图，实现目标区域中目标土壤性质含量的预测；

步骤m.分别针对各个二级区域，采用步骤i至步骤j的方法，获得各二级区域分别所对应最优自变量图层集合，然后进入步骤n；

步骤n.若r_ols_mean≥r_nls_mean，则分别针对各个二级区域，针对二级区域所对应各采样点位置，由该二级区域所对应最优自变量图层集合中提取各自变量数据值，并训练其与土壤因变量数据值之间的线性回归模型，构成该二级区域预测模型；进而获得各个二级区域预测模型，并进入步骤o；

若r_nls_mean>r_ols_mean，则分别针对各个二级区域，针对二级区域所对应各采样点位置，由该二级区域所对应最优自变量图层集合中提取各自变量数据值，并训练其与土壤因变量数据值之间的非线性回归模型，构成该二级区域预测模型；进而获得各个二级区域预测模型，并进入步骤o；

步骤o.分别针对各个二级区域，根据二级区域所对应最优自变量图层集合，应用该二级区域预测模型，获得该二级区域中土壤因变量空间分布图；进而获得各二级区域中土壤因变量空间分布图，通过组合构成目标区域中目标土壤性质空间分布图，实现目标区域中目标土壤性质含量的预测。

作为本发明的一种优选技术方案，还包括步骤h-i和步骤h-m分别如下，且步骤h如下：

步骤h.若不存在二级区域，则进入步骤h-i；

若存在二级区域，当r_ols均大于r_ols_mean、r_nls_mean，或者r_nls均大于r_ols_mean、r_nls_mean，则进入步骤h-i；

当r_ols_mean均大于r_ols、r_nls，或者r_nls_mean均大于r_ols、r_nls，则进入步骤h-m；

步骤h-i.若r_ols≥r_nls，则应用步骤g中一级区域的线性回归模型，针对目标区域中缺失土壤因变量数据值的各采样点位置，进行土壤因变量数据值预测补充，然后进入步骤i；

若r_nls>r_ols，则应用步骤g中一级区域的非线性回归模型，针对目标区域中缺失土壤因变量数据值的各采样点位置，进行土壤因变量数据值预测补充，然后进入步骤i；

步骤h-m.若r_ols_mean≥r_nls_mean，则分别应用步骤g中各二级区域的线性回归模型，针对目标区域中缺失土壤因变量数据值的各采样点位置，进行土壤因变量数据值预测补充，然后进入步骤m；

若r_nls_mean>r_ols_mean，则分别应用步骤g中各二级区域的非线性回归模型，针对目标区域中缺失土壤因变量数据值的各采样点位置，进行土壤因变量数据值预测补充，然后进入步骤m。

作为本发明的一种优选技术方案，所述步骤a包括如下步骤：

步骤a1.由指定各个数据源中的已有土壤数据，针对目标区域中预设各采样点位置，分别进行包含目标土壤性质在内的各个预设土壤物理化学性质的数据值收集操作,然后进入步骤a2；

步骤a2.选择满足对应各土壤物理化学性质的数据值均为非空要求的各个采样点位置，并以该各采样点位置的最小外接多边形，构成一级区域，且该各采样点位置作为一级区域所对应的各采样点位置，然后进入步骤a3；

步骤a3.定义目标土壤性质为土壤因变量，除目标土壤性质以外的各土壤物理化学性质构成土壤自变量集合，然后进入步骤b。

作为本发明的一种优选技术方案，所述步骤b包括如下步骤：

步骤b1.获得覆盖一级区域、与土壤因变量相关各指定环境变量的图层，然后进入步骤b2；

步骤b2.将各指定环境变量的图层分别转换为环境变量栅格图层，其中，若环境变量包含至少一个波段，则该环境变量的各波段分别转换为相对应的环境变量栅格图层，然后进入步骤b3；

步骤b3.使用双线性内插法,针对所有环境变量栅格图层进行重采样，统一栅格数据的空间分辨率为预设空间分辨率，然后进入步骤b4；

步骤b4.获得所有环境变量栅格图层上对应一级区域的区域，并分别针对一级区域所对应的各采样点位置，提取采样点位置所对应各指定环境变量的数据值，然后进入步骤b5；

步骤b5.将该各指定环境变量加入土壤自变量集合中，实现对土壤自变量集合的更新,然后进入步骤c。

作为本发明的一种优选技术方案，所述步骤c包括如下步骤：

步骤c1.针对一级区域所对应的各采样点位置，训练土壤因变量数据值与土壤自变量集合中各自变量数据值之间的线性回归模型，并获得土壤自变量集合中各自变量的确定系数然后进入步骤c2；表示土壤自变量集合中第k个自变量的确定系数；

步骤c2.分别针对土壤自变量集合中各个自变量，按的计算结果，获得各个自变量方差膨胀系数，然后进入步骤c3；

步骤c3.判断土壤自变量集合中各自变量方差膨胀系数是否均小于预设系数阈值，是则进入步骤c4；否则删除土壤自变量集合中最大方差膨胀系数的自变量，更新土壤自变量集合，并返回步骤c1；

步骤c4.针对一级区域所对应的各采样点位置，计算获得土壤因变量数据值分别与土壤自变量集合中各自变量数据值之间的相关性，并删除土壤自变量集合中相关性低于预设相关性显著差异阈值的各个自变量，更新土壤自变量集合，然后进入步骤d。

作为本发明的一种优选技术方案，所述步骤d中，在完成预设迭代次数的训练后，将被选中次数最高的临时最优自变量集合作为一级区域所对应的待选最优自变量集合，然后还包括如下步骤：

步骤d1.继续采用逐步多元线性回归模型，基于预设增幅迭代次数，继续训练采样点位置土壤因变量数据值与土壤自变量集合中各土壤自变量数据值之间的线性关系，分别获取每次迭代训练中所筛选的临时最优自变量集合，并继续统计不同临时最优自变量集合分别被选中的次数；待完成预设增幅迭代次数的训练后，将被选中次数最高的临时最优自变量集合作为一级区域所对应的待选最优自变量集合，然后进入步骤d2；

步骤d2.判断最新所获一级区域对应的两个待选最优自变量集合是否一致，是则将该待选最优自变量集合作为一级区域所对应的最优自变量集合，并进入步骤e；否则返回步骤d1。

作为本发明的一种优选技术方案，所述步骤e包括如下步骤：

步骤e1.获得覆盖一级区域的土地利用图层和成土母质图层，并针对一级区域所对应的各采样点位置，提取该各采样点位置分别所在土地利用划分区域、成土母质划分区域，然后进入步骤e2；

步骤e2.基于一级区域所对应各采样点位置的土壤因变量数据值，使用duncan多重比较分析方法，分析获得不同土地利用划分区域之间对应土壤因变量的差异性结果，以及分析获得不同成土母质划分区域之间对应土壤因变量的差异性结果，然后进入步骤e3；

步骤e3.若不同土地利用划分区域之间对应土壤因变量的差异性结果、以及不同成土母质划分区域之间对应土壤因变量的差异性结果，均不大于预设显著差异阈值，则进入步骤g；否则进入步骤e4；

步骤e4.若不同土地利用划分区域之间对应土壤因变量的差异性结果中，存在大于预设显著差异阈值的差异性结果，且不同成土母质划分区域之间对应土壤因变量的差异性结果，均不大于预设显著差异阈值，则针对其中差异性结果不大于预设显著差异阈值的不同土地利用划分区域进行合并，构成各个二级区域，然后进入步骤e7；否则进入步骤e5；

步骤e5.若不同成土母质划分区域之间对应土壤因变量的差异性结果中，存在大于预设显著差异阈值的差异性结果，且不同土地利用划分区域之间对应土壤因变量的差异性结果，均不大于预设显著差异阈值，则针对其中差异性结果不大于预设显著差异阈值的不同成土母质划分区域进行合并，构成各个二级区域，然后进入步骤e7；否则进入步骤e6；

步骤e6.若不同成土母质划分区域之间对应土壤因变量的差异性结果中、以及不同土地利用划分区域之间对应土壤因变量的差异性结果中，均存在大于预设显著差异阈值的差异性结果，则针对其中差异性结果不大于预设显著差异阈值的不同成土母质划分区域进行合并，构成各个二级区域，以及针对其中差异性结果不大于预设显著差异阈值的不同土地利用划分区域进行合并，构成各个二级区域，然后进入步骤e7；

步骤e7.将土地利用图层中合并所得各个二级区域、以及未合并的各土地利用划分区域，与成土母质图层中合并所得各个二级区域、以及未合并的各成土母质划分区域，进行空间叠加，获得各个二级区域，并基于一级区域所对应的各采样点位置，获得各个二级区域分别所对应的各采样点位置，然后进入步骤f。

作为本发明的一种优选技术方案，所述步骤g包括如下步骤：

步骤g1.针对一级区域所对应的各采样点位置，划分其中第一预设比例数量的各采样点位置，作为训练样本，剩余各采样点位置作为验证样本，然后进入步骤g2，第一预设比例大于50％；

步骤g2.针对训练样本中的各采样点位置，训练土壤因变量数据值与对应最优自变量集合中各自变量数据值之间的线性回归模型ols，并进入步骤g3；

步骤g3.针对验证样本中各采样点位置对应相应最优自变量集合中各自变量的数据值，应用该线性回归模型ols，获得验证样本中各采样点位置所对应土壤因变量预测数据值，并进入步骤g4；

步骤g4.计算验证样本中各采样点位置所对应土壤因变量数据值、与所对应土壤因变量预测数据值之间的确定系数，即一级区域所对应的线性回归模型确定系数r_ols，然后进入步骤g5；

步骤g5.分别针对一级区域所对应最优自变量集合中的各个自变量，针对训练样本中各采样点位置土壤因变量数据值与对应自变量的数据值，进行预设各指定函数的拟合，并选择预测精度最高的函数，作为该自变量所对应的非线性拟合方式；进而获得该最优自变量集合中各自变量分别所对应的非线性拟合方式，然后进入步骤g6；

步骤g6.根据一级区域所对应最优自变量集合中各自变量分别所对应的非线性拟合方式，使用非线性最小二乘法，针对训练样本中的各采样点位置，训练土壤因变量数据值与对应最优自变量集合中各自变量数据值之间的非线性回归模型nls，并进入步骤g7；

步骤g7.针对验证样本中各采样点位置对应相应最优自变量集合中各自变量的数据值，应用该非线性回归模型nls，获得验证样本中各采样点位置所对应土壤因变量预测数据值，并进入步骤g8；

步骤g8.计算验证样本中各采样点位置所对应土壤因变量数据值、与所对应土壤因变量预测数据值之间的确定系数，即一级区域所对应的非线性回归模型确定系数r_nls，然后进入步骤g9；

步骤g9.若不存在二级区域，则直接进入步骤h；若存在二级区域，则进入步骤g10；

步骤g10.分别针对各个二级区域，执行步骤g1至步骤g8的方法，获得各二级区域分别所对应的线性回归模型确定系数、以及非线性回归模型确定系数；并进一步获得所有二级区域所对应的线性回归模型确定系数的均值r_ols_mean、以及非线性回归模型确定系数的均值r_nls_mean，然后进入步骤h。

作为本发明的一种优选技术方案，所述步骤i包括如下步骤：

步骤i1.基于一级区域所对应的各个采样点位置、以及所对应的最优自变量集合，分别针对该最优自变量集合中的各个土壤物理化学性质，根据该各采样点位置分别对应土壤物理化学性质数据值、以及分别对应步骤b中各指定环境变量数据值，使用十折交叉验证的方式，针对指定各预测模型进行训练、获得各个预测模型，并选择最高预测精度的预测模型作为该土壤物理化学性质基于步骤b中全部指定环境变量的预测模型；进而获得该最优自变量集合中各土壤物理化学性质分别基于步骤b中全部指定环境变量的预测模型，然后进入步骤i2；

步骤i2.根据一级区域所对应最优自变量集合中、各土壤物理化学性质分别基于步骤b中全部指定环境变量的预测模型，结合步骤b中各指定环境变量图层，获得该最优自变量集合中各土壤物理化学性质分别对应一级区域的空间分布预测图层。

本发明所述一种基于土壤传递函数的目标土壤性质含量预测方法，采用以上技术方案与现有技术相比，具有以下技术效果：

(1)本发明所设计基于土壤传递函数的目标土壤性质含量预测方法中，所提出样点尺度的土壤传递函数，能够充分利用现有的地理要素信息，改进目标土壤性质含量预测精度低的难题，能够直接服务于国家自然资源调查数据监测补充、更新，也能为动态的生态模型、地表过程模拟中的数据补充提供技术服务；尤其是预测过程中对环境变量的动态筛选机制，修正了传统预测技术的局限性，实现了“有限资源，多源应用”的通用土壤性质预测技术，在农业应用、国土资源等部门具有广阔的工业化应用前景；

(2)本发明所设计基于土壤传递函数的目标土壤性质含量预测方法中，所提出目标土壤性质含量空间异质性的分区机制，更能准确地度量土壤传递函数拟合过程中变量与预测函数的不确定，动态筛选最优自变量集合的技术规程，不仅能够量化相关生产流程中涉及到的不确定性，也能最大程度上确定土壤传递函数所需的最优因变量集合，进而显著提升了本发明的普适性与稳健性；

(3)本发明所设计基于土壤传递函数的目标土壤性质含量预测方法，有别于传统的面向样点的土壤传递函数，所提出的技术流程涵盖了土壤图与测定土壤理化性质的映射机制，能够改进面向样点尺度的土壤传递函数，优化函数参数对土壤图的兼容性，进而将拟合的函数升尺度至不同的研究区域，实现覆盖区域尺度的土壤图制作；该技术充分利用了现有地理信息系统的技术优势，能够为更多应用部门提供更为迫切的土壤图产品。

附图说明

图1是本发明所设计基于土壤传递函数的目标土壤性质含量预测方法的步骤流程图；

图2是本发明中原始土壤数据集合与核心土壤数据集合构建示意图；

图3是本发明中包含了2种土地利用类型的二级区域划分示意图；

图4是本发明中包含了3种成土母质类型的二级区域划分示意图；

图5是本发明中包含了2种土地利用类型与3种成土母质类型的二级区域划分示意图；

图6是本发明中栅格环境变量图层与土壤样点的示意图；

图7是本发明实施例中基于两类成土母质的二级区域图层与采样点空间分布；

图8是本发明实施例中覆盖一级区域的高程图层；

图9是本发明实施例中覆盖一级区域的年均降雨图层；

图10是本发明实施例中预测生成最优自变量集合中有效锌含量的空间分布图；

图11是本发明实施例中预测生成土壤因变量的空间分布图。

具体实施方式

下面结合说明书附图对本发明的具体实施方式作进一步详细的说明。

本发明所设计一种基于土壤传递函数的目标土壤性质含量预测方法，基本思想是在收集多源土壤数据集、环境变量的基础上，划分包含全部测定信息的数据集，根据土壤性质的空间异质性划分二级区域，筛选不同区域土壤传递函数的最优自变量集合，进而面向不同分区进行线性、非线性土壤传递函数拟合。通过不同分区、不同函数的精度对比，遴选最优的面向样点的土壤传递函数，用以完善土壤样点数据库。使用较为成熟的机器学习构建区域的土壤图，提取土样样点的实验室分析数据与土壤图的数据，对比分析其误差，更新训练面向样点的土壤传递函数为面向区域的土壤传递函数，制作生产目标区域的目标土壤性质含量空间分布图。

本发明设计了一种基于土壤传递函数的目标土壤性质含量预测方法，用于实现目标区域中目标土壤性质含量的预测，实际应用当中，如图1所示，具体执行如下步骤a至步骤o。

步骤a.基于已有土壤数据，选择目标区域中满足对应预设各土壤物理化学性质的数据值均为非空要求的各个采样点位置，并以该各采样点位置的最小外接多边形，构成一级区域，且该各采样点位置作为一级区域所对应的各采样点位置，预设各土壤物理化学性质中包含目标土壤性质，定义目标土壤性质为土壤因变量，除目标土壤性质以外的各土壤物理化学性质构成土壤自变量集合，然后进入步骤b。

在具体实施中，上述步骤a具体执行如下步骤a1至步骤a3。

步骤a1.由指定各个数据源中的已有土壤数据，针对目标区域中预设各采样点位置，分别进行包含目标土壤性质在内的各个预设土壤物理化学性质的数据值收集操作,诸如图2所示，其中，s_1、s_2、s_3、s_4、s_5为各个土壤物理化学性质，然后进入步骤a2。

对于各个预设土壤物理化学性质的数据值，选择同一土壤深度位置的数据值，诸如选择0-1m土壤剖面下的土壤物理化学性质的数据值，或者选择0-20cm土壤剖面下的土壤物理化学性质的数据值。

步骤a2.选择满足对应各土壤物理化学性质的数据值均为非空要求的各个采样点位置，并以该各采样点位置的最小外接多边形，构成一级区域，且该各采样点位置作为一级区域所对应的各采样点位置，然后进入步骤a3。

步骤a3.定义目标土壤性质为土壤因变量，除目标土壤性质以外的各土壤物理化学性质构成土壤自变量集合，然后进入步骤b。

步骤b.获得覆盖一级区域、与土壤因变量相关各指定环境变量的图层，分别针对一级区域所对应的各采样点位置，提取采样点位置所对应各指定环境变量的数据值，并将该各指定环境变量加入土壤自变量集合中，实现对土壤自变量集合的更新,然后进入步骤c。

在具体实施中，上述步骤b具体执行如下步骤b1至步骤b5。

步骤b1.获得覆盖一级区域、与土壤因变量相关各指定环境变量的图层，然后进入步骤b2。这些环境变量在一定程度上影响了土壤的形成与演化，诸如下表1所示部分可供选择的环境变量图层。

表1

注：环境变量图层可以是矢量的shapefile数据格式，也可以是栅格格式(如tiff、grid)。

步骤b2.将各指定环境变量的图层分别转换为环境变量栅格图层，其中，若环境变量包含至少一个波段，则该环境变量的各波段分别转换为相对应的环境变量栅格图层，然后进入步骤b3。

步骤b3.使用双线性内插法,针对所有环境变量栅格图层进行重采样，统一栅格数据的空间分辨率为预设空间分辨率，然后进入步骤b4。例如，一个栅格的覆盖面积为100m×100m，则其空间分辨率为100m，栅格分辨率越高，表达要素的空间详细程度越高。

实际应用中，栅格数据重采样方法不限于双线性内插法，也可以使用最邻近法、三次卷积插值法等技术。

实际应用中，所获栅格环境变量图层与土壤样点的示意图如图6所示。

步骤b4.获得所有环境变量栅格图层上对应一级区域的区域，并分别针对一级区域所对应的各采样点位置，提取采样点位置所对应各指定环境变量的数据值，然后进入步骤b5。

步骤b5.将该各指定环境变量加入土壤自变量集合中，实现对土壤自变量集合的更新,然后进入步骤c。

步骤c.删除土壤自变量集合中引起多重共线性的各自变量、以及与土壤因变量相关性结果低于预设相关性显著差异阈值的各自变量，实现对土壤自变量集合的更新，然后进入步骤d。

在具体实施中，上述步骤c具体执行如下步骤c1至步骤c4。

步骤c1.针对一级区域所对应的各采样点位置，训练土壤因变量数据值与土壤自变量集合中各自变量数据值之间的线性回归模型，并获得土壤自变量集合中各自变量的确定系数然后进入步骤c2；表示土壤自变量集合中第k个自变量的确定系数。

步骤c2.分别针对土壤自变量集合中各个自变量，按的计算结果，获得各个自变量方差膨胀系数，然后进入步骤c3。

步骤c3.判断土壤自变量集合中各自变量方差膨胀系数是否均小于预设系数阈值，这里的预设系数阈值诸如设定为5，是则进入步骤c4；否则删除土壤自变量集合中最大方差膨胀系数的自变量，更新土壤自变量集合，并返回步骤c1。

步骤c4.针对一级区域所对应的各采样点位置，计算获得土壤因变量数据值分别与土壤自变量集合中各自变量数据值之间的相关性，并删除土壤自变量集合中相关性低于预设相关性显著差异阈值的各个自变量，更新土壤自变量集合，然后进入步骤d。

步骤d.针对一级区域所对应的各采样点位置，采用逐步多元线性回归模型，基于预设迭代次数，诸如100次，训练采样点位置土壤因变量数据值与土壤自变量集合中各土壤自变量数据值之间的线性关系，分别获取每次迭代训练中所筛选的临时最优自变量集合，并统计不同临时最优自变量集合分别被选中的次数；待完成预设迭代次数的训练后，将被选中次数最高的临时最优自变量集合作为一级区域所对应的最优自变量集合，然后进一步执行如下步骤d1至步骤d2。

步骤d1.继续采用逐步多元线性回归模型，基于预设增幅迭代次数，诸如50次，继续训练采样点位置土壤因变量数据值与土壤自变量集合中各土壤自变量数据值之间的线性关系，分别获取每次迭代训练中所筛选的临时最优自变量集合，并继续统计不同临时最优自变量集合分别被选中的次数；待完成预设增幅迭代次数的训练后，将被选中次数最高的临时最优自变量集合作为一级区域所对应的待选最优自变量集合，然后进入步骤d2。

步骤d2.判断最新所获一级区域对应的两个待选最优自变量集合是否一致，是则将该待选最优自变量集合作为一级区域所对应的最优自变量集合，并进入步骤e；否则返回步骤d1。

步骤e.获得覆盖一级区域的预设属性土壤区域的划分图层，并针对一级区域所对应的各采样点位置，提取该各采样点位置分别所在该预设属性下的土壤划分区域，基于该各采样点位置的土壤因变量的数据值，分析获得该不同土壤划分区域之间对应土壤因变量的差异性结果，若该各差异性结果均不大于预设显著差异阈值，则进入步骤g；若该各差异性结果中存在大于预设显著差异阈值的差异性结果，则针对其中差异性结果不大于预设显著差异阈值的不同土壤划分区域进行合并，并结合未合并的各土壤划分区域，构成各个二级区域，以及基于一级区域所对应的各采样点位置，获得各个二级区域分别所对应的各采样点位置，然后进入步骤f。

在具体实施中，上述步骤e具体执行如下步骤e1至步骤e7。

步骤e1.获得覆盖一级区域的土地利用图层和成土母质图层，并针对一级区域所对应的各采样点位置，提取该各采样点位置分别所在土地利用划分区域、成土母质划分区域，然后进入步骤e2。

步骤e2.基于一级区域所对应各采样点位置的土壤因变量数据值，使用duncan多重比较分析方法，分析获得不同土地利用划分区域之间对应土壤因变量的差异性结果，以及分析获得不同成土母质划分区域之间对应土壤因变量的差异性结果，然后进入步骤e3。

步骤e3.若不同土地利用划分区域之间对应土壤因变量的差异性结果、以及不同成土母质划分区域之间对应土壤因变量的差异性结果，均不大于预设显著差异阈值，则进入步骤g；否则进入步骤e4。

步骤e4.若不同土地利用划分区域之间对应土壤因变量的差异性结果中，存在大于预设显著差异阈值的差异性结果，且不同成土母质划分区域之间对应土壤因变量的差异性结果，均不大于预设显著差异阈值，则针对其中差异性结果不大于预设显著差异阈值的不同土地利用划分区域进行合并，构成各个二级区域，然后进入步骤e7；否则进入步骤e5。

步骤e5.若不同成土母质划分区域之间对应土壤因变量的差异性结果中，存在大于预设显著差异阈值的差异性结果，且不同土地利用划分区域之间对应土壤因变量的差异性结果，均不大于预设显著差异阈值，则针对其中差异性结果不大于预设显著差异阈值的不同成土母质划分区域进行合并，构成各个二级区域，然后进入步骤e7；否则进入步骤e6。

步骤e6.若不同成土母质划分区域之间对应土壤因变量的差异性结果中、以及不同土地利用划分区域之间对应土壤因变量的差异性结果中，均存在大于预设显著差异阈值的差异性结果，则针对其中差异性结果不大于预设显著差异阈值的不同成土母质划分区域进行合并，构成各个二级区域，以及针对其中差异性结果不大于预设显著差异阈值的不同土地利用划分区域进行合并，构成各个二级区域，然后进入步骤e7。

步骤e7.将土地利用图层中合并所得各个二级区域、以及未合并的各土地利用划分区域，与成土母质图层中合并所得各个二级区域、以及未合并的各成土母质划分区域，进行空间叠加，获得各个二级区域，并基于一级区域所对应的各采样点位置，获得各个二级区域分别所对应的各采样点位置，然后进入步骤f。

实际应用中，诸如包含了2种土地利用类型的二级区域划分如图3所示；包含了3种成土母质类型的二级区域划分如图4所示；包含了2种土地利用类型与3种成土母质类型的二级区域划分如图5所示。

步骤f.分别针对各个二级区域，采用步骤d的方法，获得各个二级区域分别所对应的最优自变量集合，并进入步骤g。

步骤g.针对一级区域所对应的各采样点位置，训练土壤因变量数据值与对应最优自变量集合中各自变量数据值之间的线性回归模型、非线性回归模型，并获得该线性回归模型的确定系数、以及非线性回归模型的确定系数，即一级区域所对应的线性回归模型确定系数r_ols、以及非线性回归模型确定系数r_nls。

进一步若不存在二级区域，则直接进入步骤h；若存在二级区域，则分别针对各个二级区域，训练对应各采样点位置土壤因变量数据值与对应最优自变量集合中各自变量数据值之间的线性回归模型、非线性回归模型，并获得该线性回归模型的确定系数、以及非线性回归模型的确定系数，进而获得各二级区域分别所对应的线性回归模型确定系数、以及非线性回归模型确定系数，并进一步获得所有二级区域所对应的线性回归模型确定系数的均值r_ols_mean、以及非线性回归模型确定系数的均值r_nls_mean；然后进入步骤h。

在具体实施中，上述步骤g具体执行如下步骤g1至步骤g10。

步骤g1.针对一级区域所对应的各采样点位置，划分其中第一预设比例数量的各采样点位置，作为训练样本，剩余各采样点位置作为验证样本，然后进入步骤g2，第一预设比例大于50％，诸如75％。

步骤g2.针对训练样本中的各采样点位置，训练土壤因变量数据值与对应最优自变量集合中各自变量数据值之间的线性回归模型ols，并进入步骤g3。

步骤g3.针对验证样本中各采样点位置对应相应最优自变量集合中各自变量的数据值，应用该线性回归模型ols，获得验证样本中各采样点位置所对应土壤因变量预测数据值，并进入步骤g4。

步骤g4.计算验证样本中各采样点位置所对应土壤因变量数据值、与所对应土壤因变量预测数据值之间的确定系数，即一级区域所对应的线性回归模型确定系数r_ols，然后进入步骤g5。

步骤g5.分别针对一级区域所对应最优自变量集合中的各个自变量，针对训练样本中各采样点位置土壤因变量数据值与对应自变量的数据值，进行预设各指定函数的拟合，这里预设各指定函数，诸如包括幂函数、指数函数、双曲线函数与对数函数；然后选择预测精度最高的函数，作为该自变量所对应的非线性拟合方式；进而获得该最优自变量集合中各自变量分别所对应的非线性拟合方式，然后进入步骤g6。

步骤g6.根据一级区域所对应最优自变量集合中各自变量分别所对应的非线性拟合方式，使用非线性最小二乘法，针对训练样本中的各采样点位置，训练土壤因变量数据值与对应最优自变量集合中各自变量数据值之间的非线性回归模型nls，并进入步骤g7。

步骤g7.针对验证样本中各采样点位置对应相应最优自变量集合中各自变量的数据值，应用该非线性回归模型nls，获得验证样本中各采样点位置所对应土壤因变量预测数据值，并进入步骤g8。

步骤g8.计算验证样本中各采样点位置所对应土壤因变量数据值、与所对应土壤因变量预测数据值之间的确定系数，即一级区域所对应的非线性回归模型确定系数r_nls，然后进入步骤g9。

步骤g9.若不存在二级区域，则直接进入步骤h；若存在二级区域，则进入步骤g10。

步骤g10.分别针对各个二级区域，执行步骤g1至步骤g8的方法，获得各二级区域分别所对应的线性回归模型确定系数、以及非线性回归模型确定系数；并进一步获得所有二级区域所对应的线性回归模型确定系数的均值r_ols_mean、以及非线性回归模型确定系数的均值r_nls_mean，然后进入步骤h。

步骤h.若不存在二级区域，则进入步骤h-i；

若存在二级区域，当r_ols均大于r_ols_mean、r_nls_mean，或者r_nls均大于r_ols_mean、r_nls_mean，则进入步骤h-i；

当r_ols_mean均大于r_ols、r_nls，或者r_nls_mean均大于r_ols、r_nls，则进入步骤h-m。

步骤h-i.若r_ols≥r_nls，则应用步骤g中一级区域的线性回归模型，针对目标区域中缺失土壤因变量数据值的各采样点位置，进行土壤因变量数据值预测补充，然后进入步骤i；

若r_nls>r_ols，则应用步骤g中一级区域的非线性回归模型，针对目标区域中缺失土壤因变量数据值的各采样点位置，进行土壤因变量数据值预测补充，然后进入步骤i。

步骤h-m.若r_ols_mean≥r_nls_mean，则分别应用步骤g中各二级区域的线性回归模型，针对目标区域中缺失土壤因变量数据值的各采样点位置，进行土壤因变量数据值预测补充，然后进入步骤m；

若r_nls_mean>r_ols_mean，则分别应用步骤g中各二级区域的非线性回归模型，针对目标区域中缺失土壤因变量数据值的各采样点位置，进行土壤因变量数据值预测补充，然后进入步骤m。

步骤i.基于一级区域所对应的各个采样点位置、以及所对应的最优自变量集合，根据该各采样点位置分别对应该最优自变量集合中各土壤物理化学性质的数据值，获得该最优自变量集合中各土壤物理化学性质分别基于步骤b中全部指定环境变量的预测模型；然后结合步骤b中各指定环境变量图层，获得该最优自变量集合中各土壤物理化学性质分别对应一级区域的空间分布预测图层，然后进入步骤j。

在具体实施中，上述步骤i具体执行如下步骤i1至步骤i2。

步骤i1.基于一级区域所对应的各个采样点位置、以及所对应的最优自变量集合，分别针对该最优自变量集合中的各个土壤物理化学性质，根据该各采样点位置分别对应土壤物理化学性质数据值、以及分别对应步骤b中各指定环境变量数据值，使用十折交叉验证的方式，针对指定各预测模型进行训练、获得各个预测模型，这里各预测模型进行训练，诸如包括地理加权回归、普通克里格、回归克里格、人工神经网络、增强回归树。

然后选择最高预测精度的预测模型作为该土壤物理化学性质基于步骤b中全部指定环境变量的预测模型；进而获得该最优自变量集合中各土壤物理化学性质分别基于步骤b中全部指定环境变量的预测模型，然后进入步骤i2。

步骤i2.根据一级区域所对应最优自变量集合中、各土壤物理化学性质分别基于步骤b中全部指定环境变量的预测模型，结合步骤b中各指定环境变量图层，获得该最优自变量集合中各土壤物理化学性质分别对应一级区域的空间分布预测图层。

步骤j.将一级区域所对应最优自变量集合中各土壤物理化学性质的空间分布预测图层、与该最优自变量集合中各环境变量对应一级区域的图层进行合并，构成一级区域所对应最优自变量图层集合，然后进入步骤k。

步骤k.若r_ols≥r_nls，则针对一级区域所对应的各采样点位置，由一级区域所对应最优自变量图层集合中提取各自变量数据值，并训练其与土壤因变量数据值之间的线性回归模型，构成一级区域预测模型，并进入步骤l；

若r_nls>r_ols，则针对一级区域所对应的各采样点位置，由一级区域所对应最优自变量图层集合中提取各自变量数据值，并训练其与土壤因变量数据值之间的非线性回归模型，构成一级区域预测模型，并进入步骤l。

步骤l.根据一级区域所对应最优自变量图层集合，应用一级区域预测模型，获得土壤因变量空间分布图，即目标区域中目标土壤性质空间分布图，实现目标区域中目标土壤性质含量的预测。

步骤m.分别针对各个二级区域，采用步骤i至步骤j的方法，获得各二级区域分别所对应最优自变量图层集合，然后进入步骤n。

步骤n.若r_ols_mean≥r_nls_mean，则分别针对各个二级区域，针对二级区域所对应各采样点位置，由该二级区域所对应最优自变量图层集合中提取各自变量数据值，并训练其与土壤因变量数据值之间的线性回归模型，构成该二级区域预测模型；进而获得各个二级区域预测模型，并进入步骤o；

若r_nls_mean>r_ols_mean，则分别针对各个二级区域，针对二级区域所对应各采样点位置，由该二级区域所对应最优自变量图层集合中提取各自变量数据值，并训练其与土壤因变量数据值之间的非线性回归模型，构成该二级区域预测模型；进而获得各个二级区域预测模型，并进入步骤o。

步骤o.分别针对各个二级区域，根据二级区域所对应最优自变量图层集合，应用该二级区域预测模型，获得该二级区域中土壤因变量空间分布图；进而获得各二级区域中土壤因变量空间分布图，通过组合构成目标区域中目标土壤性质空间分布图，实现目标区域中目标土壤性质含量的预测。

针对本发明所设计基于土壤传递函数的目标土壤性质含量预测方法，下面以安徽省宣城市研究样区的土壤有效铜含量预测为具体实施例，进行具体介绍。

宣城是安徽省地级市，地处安徽省东南部，是皖苏浙交汇区域中心城市，东南沿海沟通内地的重要通道。近年来，工业和城市的飞速发展导致了重金属的持续排放和积累，对粮食生产与生态环境造成了严重的影响。因为土壤铜不仅涉及到土壤重金属污染治理问题，土壤有效铜又是作物生长发育必要的微量元素，土壤有效铜含量技术一直备受关注。

应用本发明所设计预测方法，具体实现土壤有效铜预测，实现对数据库中缺少的有效铜数据进行补充，并结合环境变量图层完成该区域的土壤有效铜含量空间分布图的制作，按图1所示，具体执行过程如下。

步骤a1.由指定各个数据源中的已有土壤数据，针对目标区域中预设各采样点位置，基于20cm土样采集深度，分别进行土壤的有效铜含量、有机质含量、有效磷含量、有效钾含量、有效铁含量、有效锰含量、有效锌含量、ph、全氮含量的数据值收集操作,然后进入步骤a2。

步骤a2.选择满足对应各土壤物理化学性质的数据值均为非空要求的各个采样点位置，此实施例下即为383个采样点位置，并以该383个采样点位置的最小外接多边形，构成一级区域，且该各采样点位置作为一级区域所对应的各采样点位置，然后进入步骤a3。

步骤a3.这里土壤因变量即为有效铜含量，有机质含量、有效磷含量、有效钾含量、有效铁含量、有效锰含量、有效锌含量、ph、全氮含量构成土壤自变量集合，然后进入步骤b。

按如下步骤b1至步骤b5，执行步骤b。

步骤b1.获得覆盖一级区域、与土壤因变量相关各指定环境变量的图层，包括高程(dem)、坡度(slope)、剖面曲率(procur)、平面曲率(plancur)、地形湿度指数(twi)、年均降雨(map)、年均气温(mat)、年均土壤温度(soiltemp)、年平均日照(solar)、归一化植被指数(ndvi)与净初级生产力(npp)，诸如覆盖一级区域的高程图层如图8所示，覆盖一级区域的年均降雨图层如图9所示。

然后基于空间分辨率500m的设定，执行步骤b2至步骤b4,然后执行步骤b5，将该各指定环境变量加入土壤自变量集合中，对土壤自变量集合更新为{som,ap,ak,afe,amn,azn,ph,tn,dem,slope,procur,plancur,twi,map,mat,soiltemp,solar,ndvi,npp}，然后进入步骤c。

步骤c.删除土壤自变量集合中引起多重共线性的各自变量、以及与土壤因变量有效铜含量相关性结果低于预设相关性显著差异阈值的各自变量，实现对土壤自变量集合的更新，更新后的土壤自变量集合为{ap,ak,afe,azn,ph,tn,dem,slope,procur,map,solar,ndvi}，然后进入步骤d。

按上述步骤d的描述进行执行，获得一级区域所对应的最优自变量集合{azn,ph,tn,dem,map}，并进入步骤e；

步骤e中执行如下步骤e1至步骤e7。

步骤e1.获得覆盖一级区域的土地利用图层和成土母质图层，并针对一级区域所对应的各采样点位置，提取该各采样点位置分别所在土地利用划分区域、成土母质划分区域，然后进入步骤e2。

步骤e2.基于一级区域所对应各采样点位置的土壤因变量数据值，使用duncan多重比较分析方法，分析获得不同土地利用划分区域之间对应土壤因变量的差异性结果，以及分析获得不同成土母质划分区域之间对应土壤因变量的差异性结果，然后进入步骤e3。

经过步骤e1、e2，分析可知对应本实施例中的383个采样点位置的有效铜含量，不同成土母质划分区域之间对应有效铜含量的差异性结果中，存在大于预设显著差异阈值的差异性结果，且不同土地利用划分区域之间对应有效铜含量的差异性结果，均不大于预设显著差异阈值，

由于该地区共四种成土母质，石灰质沉积岩及相应的变质岩风化物、浅色结晶岩风化物、碎屑沉积岩及相应的变质岩风化物与黄土。

则根据不同土地利用划分区域之间对应有效铜含量的差异性结果，成土母质类型分为两类：a类(石灰质沉积岩及相应的变质岩风化物)与b类(浅色结晶岩风化物、碎屑沉积岩及相应的变质岩风化物与黄土)，每一类合并后的成土母质类型覆盖的区域为一个二级区域，则基于两类成土母质的二级区域如图7所示，然后进入步骤e7。

步骤e7.将土地利用图层中合并所得各个二级区域、以及未合并的各土地利用划分区域，与成土母质图层中合并所得各个二级区域、以及未合并的各成土母质划分区域，进行空间叠加，获得各个二级区域，并基于一级区域所对应的各采样点位置，获得各个二级区域分别所对应的各采样点位置，然后进入步骤f。

步骤f.分别针对各个二级区域，采用步骤d的方法，获得各个二级区域分别所对应的最优自变量集合，并进入步骤g。

通过执行如下步骤g1至步骤g10，实现步骤g的执行。

步骤g1.针对一级区域所对应的各采样点位置，划分其中75％的各采样点位置，作为训练样本，剩余25％的各采样点位置作为验证样本，然后进入步骤g2。

步骤g2.针对训练样本中的各采样点位置，训练土壤因变量数据值与对应最优自变量集合{azn,ph,tn,dem,map}中各自变量数据值之间的线性回归模型ols如下：

acu＝-5.453+0.802×azn+0.615×ph+0.712×tn-0.00552×dem+0.00232×map

然后进入步骤g3。

然后执行步骤g3至步骤g4，获得一级区域所对应的线性回归模型确定系数r_ols＝0.51，然后进入步骤g5。

步骤g5.分别针对一级区域所对应最优自变量集合中的各个自变量，针对训练样本中各采样点位置土壤因变量数据值与对应自变量的数据值，分别进行包括幂函数、指数函数、双曲线函数与对数函数的拟合；然后选择预测精度最高的函数，作为该自变量所对应的非线性拟合方式；进而获得该最优自变量集合中各自变量分别所对应的非线性拟合方式，然后进入步骤g6。

进一步依次执行步骤g6至步骤g8，获得一级区域所对应的非线性回归模型确定系数r_nls＝0.46，然后进入步骤g9。

步骤g9.若不存在二级区域，则直接进入步骤h；若存在二级区域，则进入步骤g10。

步骤g10.分别针对各个二级区域，执行步骤g1至步骤g8的方法，获得各二级区域分别所对应的线性回归模型确定系数、以及非线性回归模型确定系数；并进一步获得所有二级区域所对应的线性回归模型确定系数的均值r_ols_mean＝0.45、以及非线性回归模型确定系数的均值r_nls_mean＝0.37，然后进入步骤h。

基于步骤h与步骤h-i的执行，根据r_ols≥r_nls，且r_ols≥r_ols_mean，且r_ols≥r_nls_mean，则应用步骤g中一级区域的线性回归模型，针对目标区域中缺失土壤因变量数据值的各采样点位置，进行土壤因变量数据值预测补充，然后进入步骤i。

通过执行上述步骤i1至步骤i2的描述，完成步骤i，获得一级区域所对应最优自变量集合中各土壤物理化学性质分别对应一级区域的空间分布预测图层，诸如预测生成覆盖一级区域的有效锌含量图层如图10所示，然后进入步骤j。

步骤j.将一级区域所对应最优自变量集合中各土壤物理化学性质的空间分布预测图层、与该最优自变量集合中各环境变量对应一级区域的图层进行合并，构成一级区域所对应最优自变量图层集合，然后进入步骤k。

步骤k.根据r_ols≥r_nls，则针对一级区域所对应的各采样点位置，由一级区域所对应最优自变量图层集合中提取各自变量数据值，并训练其与土壤因变量数据值之间的线性回归模型如下：

acu＝-3.459+1.249×azn+0.939×ph+0.127×tn-0.00509×dem-0.000522×map

即构成一级区域预测模型，并进入步骤l。

步骤l.根据一级区域所对应最优自变量图层集合，应用一级区域预测模型，获得土壤因变量空间分布图，即目标区域中有效铜含量空间分布图，如图11所示，实现目标区域中目标土壤性质含量的预测。

本发明所设计基于土壤传递函数的目标土壤性质含量预测方法，在面向样点的土壤数据预测中考虑了环境变量与不确定性分析，在面向区域的数字土壤制图中集成了土壤传递函数与临时生产制作的土壤图，避免了土壤数据样点预测与区域制图中的不确定性，有效解决了传统数字土壤制图方法中环境变量与土壤理化性质相关性低而导致生产制作的土壤图精度低的技术瓶颈。本发明的方法具有较好的移植性，不仅能够应用于不同尺度、不同土壤物理化学性质的土壤图制作，也能应用与不同规模的土壤数据库完善。所提出技术有待于在更多的技术领域应用，以检验其性能。

上面结合附图对本发明的实施方式作了详细说明，但是本发明并不限于上述实施方式，在本领域普通技术人员所具备的知识范围内，还可以在不脱离本发明宗旨的前提下做出各种变化。