一种基于连续生理数据的个体化状态监测分析方法和设备与流程

本发明涉及人体生理参数的监测和分析技术，尤其涉及一种通过可穿戴设备获取建册对象的基本生理信号，对连续生理信号进行学习，进而对生理状态变化进行量化分析的方法和设备。
背景技术：
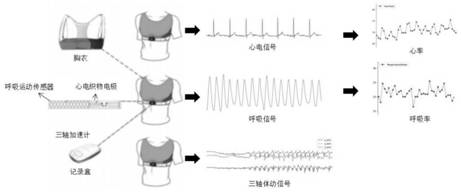
：监护技术在上世纪就已经出现了。从早期的床旁监护，到移动监护，进而到现在的穿戴式生理监护。在生理监护领域，有一个重要的概念就是如何刻画生理状态的变化，对这种生理状态的变化进行量化。传统的方法往往是依赖人为经验来观察某一项或某几项生理指标绝对数值的变化，当观察的指标超过一定的阈值之后，观察者就会认为该状态发生了异常，从而做出下一步的应变措施。这种主观经验方法目前在绝大多数工业和产业界都是主要的方法。但随着系统的日趋复杂，这种方法已不再能够满足任务的实际需要，其原因在于很多问题中阈值的确立伴随着很强的个人主观性，对于复杂系统，个人的经验很多时候是不准的；另一方面，由于系统的复杂性，当观察的指标超过实际设定的阈值时，系统已经处于崩溃的状态或奔溃的边缘，这种主观经验方法无法起到一个早期报警的作用，从而限制了其在很多实际应用的效果。对于人体的状态监测来说，更是如此。人体是一个及其复杂的系统，心脏、肝、肺等器官之间有着千丝万缕的联系，很多时候如果只观察某一个器官的指标很难看出人体状态的变化，而且人与人之间的个体化差异十分大，对一个人的定下的阈值对另一个人可能不再适用，这又极大复杂了病理监护人员的工作。技术实现要素：鉴于上述问题，本申请旨在提出基于连续生理数据的个体化状态监测分析方法，其不是基于传统的阈值方法的生理参数监护分析技术，而是通过被监测对象的生理时间序列纵向对比分析，识别生理状态变化，从而实现更加灵敏的、特异性的、个体化的生理状态监测。本申请的个体化的生理状态监测分析方法，其包括：将在同一时间窗的k个生理参数的数值构成的向量作为指标向量，其中k为大于1的自然数；用该个体在正常状态下的多个指标向量构成指标数据库g；将该个体的当前时间窗的指标向量作为输入向量vin；在指标数据库g中，通过欧氏距离或者核函数来找到与所述输入向量最为接近的n个指标向量，该n个指标向量构成矩阵d；对于矩阵d的每个指标向量xj，在指标数据库中g，通过欧氏距离或者核函数来找到与其最为接近的n个指标向量并构成矩阵dj；计算该输入向量与其估计向量之间的差值，作为第一差值vre；计算矩阵d中的每个指标向量xj与其估计向量vjest的差值，作为第二差值；全部第二差值构成差值库gre；计算差值库gre的均值μ1与方差∑1；计算差值库gre的马氏距离平方最大值h：其中，xi为差值库gre中的差值向量；计算自由度为k的卡方分布0.95分位点的λ值：其中f(x)为自由度为k的卡方分布密度函数；计算得到近似真实的协方差矩阵：∑＝∑1·h/λ；计算马氏距离hre：hre＝(vre-μ1)t∑-1(vre-μ1)；然后通过自由度为k的卡方分布累积分布函数来计算sci的具体数值：优选地，所述多个生理参数中至少包括心电信号或呼吸信号。优选地，所述多个生理参数还可以包括体位信号和体动信号。优选地，所述指标数据库存储于计算平台；所述预定个数的指标向量的查找、所述估计向量的计算、所述第一差值的计算、所述第二差值的计算、所述第一差值在整个第二差值中的分布的计算、以及状态变化指数的计算均在该计算平台上进行。优选地，所述计算平台位于本地，穿戴在个体身上；所述多个生理参数由该个体所穿戴的生理参数传感器感测得到的生理信号经处理后获得；所述多个生理参数传输至所述计算平台；所述计算平台根据接收的所述多个生理参数而获得所述指标向量。优选地，所述计算平台位于远程；所述多个生理参数由该个体所穿戴的生理参数传感器感测得到的生理信号经处理后获得；所述多个生理参数通过无线传输发送到所述计算平台；所述计算平台根据接收的所述多个生理参数而获得所述指标向量。优选地，所述状态变化指数在0-1之间，数值越高表示偏离正常状态越远。优选地，如果状态变化指数大于0且小于预定值，则将该输入向量作为指标数据库的一个指标向量而纳入指标数据库。本申请的基于连续生理数据的个体化状态监测分析设备，其包括：计算平台；计算平台包括指标数据库单元、估计单元、差值单元、状态变化指数单元；计算平台被配置，用该个体的同一时间窗的k个生理参数的数值构成向量，作为指标向量；指标数据库单元用该个体在正常状态下的多个指标向量构成指标数据库g；估计单元用于计算与输入到估计单元的指标向量对应的估计向量；差值单元用于计算两个指标向量之间的差值；状态变化指数单元用于计算反映个体当前的状态偏离其正常状态的程度的状态变化指数sci；计算平台将个体的当前时间窗的指标向量作为输入向量vin，根据该输入向量vin自指标数据库单元的指标数据库g中选出与所述输入向量vin最为接近的预定个数的指标向量，估计单元根据该预定个数的指标向量计算出该输入向量的估计向量vest；该预定个数的指标向量构成矩阵d；对于矩阵d中的每个指标向量xj，计算平台自指标数据库单元的指标数据库g中找到与其最为接近的预定个数的指标向量，估计单元根据该预定个数的指标向量计算与其对应的估计向量vjest；差值单元计算出该输入向量vin与其估计向量vest之间的差值，作为第一差值vre；差值单元计算出矩阵d中的每个指标向量xj与其估计向量vjest的差值，作为第二差值，全部第二差值构成差值库gre；状态变化指数单元计算差值库gre的均值μ1与方差∑1；状态变化指数单元计算差值库gre的马氏距离平方最大值h：其中，xi为差值库gre中的差值向量；状态变化指数单元计算自由度为k的卡方分布0.95分位点的λ值：其中f(x)为自由度为k的卡方分布密度函数；状态变化指数单元计算得到近似真实的协方差矩阵：∑＝∑1·h/λ；状态变化指数单元计算马氏距离hre：hre＝(vre-μ1)t∑-1(vre-μ1)；然后状态变化指数单元通过自由度为k的卡方分布累积分布函数来计算sci的具体数值：优选地，所述设备被穿戴在该个体身上；所述多个生理参数由该个体穿戴的生理参数传感器感测得到的生理信号经处理后获得。与以往的主观经验阈值方法相比，本申请从考虑单个个体前后状态的相似性出发，考察多个指标之间的协同相似联系，从而避免了个体之间差异性大的问题。另一方面，即使某些单项指标还处在正常的波动范围里面，也能够更加早期的预测出生理状态变化情况。附图说明图1为可穿戴系统采集和发送数据流程图；图2为可穿戴系统及其采集的生理信号；图3为心率、呼吸率和三轴加速度信号及30s滑动时间窗；图4为生理状态监测分析整体流程图；图5a为实施例一的模拟高原低氧环境实验结果；图5b为实施例二的模拟高原低氧环境实验结果；图6为实施例三的突发房颤抢救患者案例。具体实施方式下面，结合附图对本申请进行详细说明。首先通过让被监测对象穿戴胸衣进行数据采集，穿戴胸衣包括带有心电导联接口、呼吸传感器、加速度传感器和血氧饱和度采集器组成，分别可以采集心电信号、呼吸信号、体位体动信号和血氧饱和度，并把采集到的信号集成到信号采集盒。数据发送模块会把采集到的数据中央计算平台，中央计算平台可以是本地的，也可以是远程的。信号流程图如图1所示。可穿戴系统可以为一背心或者胸带，采集心电、呼吸和三轴加速度传感器信号，心电信号和呼吸信号经过进一步处理，可以获得心率和呼吸率时间序列。可穿戴系统及其采集的原始生理信号(心电、呼吸、三轴加速度)以及心率和呼吸率时间序列如图2所示。对原始的心率、呼吸率信号，通过平滑滤波依次作用于各项原始信号指标，并从中提取到佩戴者心率指标、呼吸率指标、和三轴加速度指标。采用30s时间窗内(图3中黑色矩形框)的心率、呼吸率中位数组成二维向量，表征测试者当前的生命体征，通常选取被监测者健康、稳定状态下的向量来构建生理指标状态向量库。当数据传送到中央计算平台后，中央计算平台会为每个被监测者提供单独的计算资源，通过监测一段时间的生理参数，建立单独的生理指标状态库，用g表示。完成g的建立之后，即可开展个体化的生理状态监测分析，设输入指标向量为vin，给定vin后，系统会从g中找出与vin最相似的15个向量组成d矩阵，刻画相似程度可以用欧氏距离或核函数等等，这里采用⊕表示核函数运算，刻画两个向量xi与xj的相近程度由以下公式给出：其中核函数可以高斯核、三角函数核等合法核函数。在寻找最优估计向量vest时，本申请采用了三种方法。方法一，得到矩阵d后，运用优化理论，将寻找vin最优估计向量vest的问题转换成先求参数w的优化问题：w≥0其中，矩阵e使用frobenius范数，d为与vin最相近的15个向量组成的矩阵，e为形为15*15的噪声矩阵，e为形为15*1的噪声向量，w为15*1的系数向量。方法二，针对参数w要进行进一步的正则化，比如对于系数w的稀疏化，我们会将寻找最相似向量问题转换为下列的优化问题：w≥0其中，矩阵e使用frobenius范数，系数w向量使用l1范数，λ1为惩罚项系数。方法三，也可以简化噪声部分，仅仅考虑噪声向量e：w≥0其中，e为形为15*1的噪声向量，系数w的范数使用l2范数。在采用上述方法得到系数w后,可以得到与vin的最优估计向量vest：vest＝dw之后考虑vest与vin的差值vre：vre＝vin-vest通过vre可以反映这两个向量之间相似度，来刻画状态改变与否，当输入的向量vin与计算系统挑出来的向量vest很相似的时候，认为当下的生理状态没有发生太大的变化，如果输入的向量与计算系统挑出来的向量差别较大时，可以认为当下的生理状态发生了变化。除了观察vre数值的大小来反映生理状态的变化，更为稳健的方法是观察vre的分布。进一步的，基于多个生理参数的变化，可以状态变化指数(sci)进行估计。由于在模板库g样本处理时，为消除异常向量对结果的影响，我们只保留了95％分位点对应的等概率范围内的样本点，所以由此计算的残差不再是随机样本，估计到的协方差矩阵的元素绝对值偏小，所以需要推导出近似的真实协方差矩阵。通过样本g的残差gre计算其均值与方差μ1，∑1。计算其马氏距离平方最大值：其中，xi为gre中的样本残差向量。计算自由度为样本特征维度的卡方分布0.95分位点的λ值：其中f(x)为自由度为样本特征维度的卡方分布密度函数。计算得到近似真实的协方差矩阵：∑＝∑1·h/λ根据当前计算的残差vre在样本gre残差分布(μ1，∑)中的情况确定状态变化指数的大小，越接近与1表示偏离状态指标库g越远。首先计算马氏距离：hre＝(vre-μ1)t∑-1(vre-μ1)之后通过自由度为样本特征维度k的卡方分布累积分布函数来计算sci的具体数值：这时，可以根据vre偏离的情况，选择进一步将vin添加到生理指标状态向量库中，作为系统出现的一种新状态，来丰富状态指标库g。该计算平台的一大优势在于当新的状态指标数据vin来临时，可以进行定期更新，从而能够自动长时间监测，并及时作出早期预警。首先，为了验证算法的准确性与可行性，针对健康人进行了模拟高原实验，实验采用测试者日常生活中的一天的生理参数作为状态向量库g，在模拟高原低氧环境中，测试者会在模拟海拔四千米低氧的环境下分别做静止看书、快步走、高抬腿三个动作，尽量保持与前一天接近的活动强度，验证算法是否能够准确检测测试者当前的生理体征是否偏离状态向量库g。实施例一图5a为一例测试者的模拟高原低氧实验结果图，其实施的是第一种方法，图中加的血氧信号为了更好地观察测试者所处的低氧环境。在实验刚开始时，测试者还处在正常海拔下，当前的状态向量为vin＝[73.2602，25.0000]，经过相似度比较，从g中取出15个向量组成矩阵d：心率呼吸率73.26022573.71012572.37652574.44172574.44172572.02892571.85722571.85642571.68472571.34452575.28242573.34962670.92202572.99312473.620626最终计算出来的最优估计值vest＝[73.9942，25.0637]，差值vre＝[0.3160，0.0637]，计算vre在gre分布中的sci指数为0.1584，偏离状态向量库g较小。相反，我们取高原实验开始后的向量：vin＝[92.7359，22.0000]，对应的d矩阵为：心率呼吸率76.92312379.15572477.720223.578.74022476.43322380.00002577.62082474.074122.572.81602272.55232281.30322676.62952471.68552278.32902573.710121最终计算出来的最优估计值vest＝[77.7888，24.0335]，差值vre＝[14.9471，2.0335]，计算后的sci指数达到0.98，严重偏离状态向量库g。sci指数介于0-1之间，数值越高表明偏离日常状态越远。从图5a中可以看出，测试者在低氧环境下生理状态发生改变(血氧饱和度降低)，sci指数也明显增大，能够有效表征被测试者生理状态变化。实施例二图5b为一例测试者的模拟高原低氧实验结果图，其中图5b实施的是第二种方法，图中加的血氧信号为了更好地观察测试者所处的低氧环境。在实验刚开始时，测试者还处在正常海拔下，当前的状态向量为vin＝[68.1818，22.0000]，经过相似度比较，从g中取出15个向量组成矩阵d：心率呼吸率68.37662267.79662268.96552267.23162267.22742269.16482267.03912267.03912268.18182368.18182168.37662365.93412267.79662167.79662165.934122最终计算出来的最优估计值vest＝[67.8312，21.9314]，差值vre＝[0.3505，0.0685]，计算vre在gre分布中的sci指数为0.0397，偏离状态向量库g较小。相反，我们取高原实验开始后的向量：vin＝[96.6186，16]，对应的d矩阵为：心率呼吸率69.97141975.47172268.96551972.28922176.923123.573.17072267.03911967.03911971.00592171.00592168.57142072.50822274.53422370.38182172.291822最终计算出来的最优估计值vest＝[75.1937，22.7126]，差值vre＝[21.4248，6.7126]，计算后的sci指数达到0.99，严重偏离状态向量库g。sci指数介于0-1之间，数值越高表明偏离日常状态越远。从图5b中可以看出，测试者在低氧环境下生理状态发生改变(血氧饱和度降低)，sci指数也明显增大，能够有效表征被测试者生理状态变化。实施例三图6为一突发严重房颤进行抢救的患者案例。图6中实施的是方法三。选取患者处于相对平稳状态下的一天的生理数据构建生理状态向量库g，图6中(a)为经过抢救治疗后生命体征平稳的某个上午的数据，比如上午08点52分左右，当前的状态向量为：vin＝[51.2820，22]，经过相似度比较，从g中取出15个向量组成矩阵d：心率呼吸率51.39212251.39212251.39212251.06382251.06382250.95562250.84752251.72412250.63292251.28212152.06102250.42022250.42022251.17292352.173922最终计算出的最优化估计值vest＝[51.2051，21.9986]，差值向量为：vre＝[0.0769，0.0014]，计算其在gre分布：中的sci值为0.0853，从图中可见其sci值绝大部分处在正常水平。图6中(b)为患者发生房颤当天采集的数据，大概在下午19点40分时，当前的输入向量为vin＝[72.5，12.5]，对应的矩阵d为：心率吁吸率51.83611450.63291351.06381452.40171650.00001352.28781650.63291450.63291449.79251353.57251849.38681351.83611650.20921450.20921450.209214计算的最优估计向量：vest＝[53.5725，18]，差值vre＝[18.9275，5.5]，计算后的sci高达0.99，根据医疗记录显示，该患者确实从下午开始就感觉身体不适，在21点50左右才发生房颤，但sci与正常水平相比，从19点40分开始，其数值一直处在较高的水平。本申请中，通过被监测对象的生理时间序列纵向对比分析，识别生理状态变化，从而实现更加灵敏的、特异性的、个体化的生理状态监测。本申请中计算平台可以以单片机、dsp、计算机等实现，指标数据库单元、估计单元、差值单元、状态变化指数单元可以是计算平台上通过程序而实现的功能模块。除非另有定义，本申请中使用的所有技术和/或科学术语具有与由本发明所涉及的领域的普通技术人员通常理解的相同含义。本申请中提到的材料、方法和实施例仅为说明性的，而非限制性的。虽然已结合具体实施方式对本发明进行了描述，在本申请的发明主旨下，本领域的技术人员可以进行适当的替换、修改和变化，这种替换、修改和变化仍属于本申请的保护范围。当前第1页12