一种近红外光无创测量人眼房水组分浓度的方法及系统与流程

本发明涉及医学领域，特别是涉及一种近红外光无创测量人眼房水组分浓度的方法及系统。

背景技术：

房水是填充于人眼角膜和虹膜晶体隔之间的空间(前房)里的液体，正常情况下无色透明、量和成分相对稳定。以较快的更新速率不断产生和排出，形成动态平衡，维持眼球内环境的稳定。

当伴有内眼的炎症、感染、外伤、手术或某些药物的作用时，房水中的蛋白质和抗体与血清中的蛋白质和抗体平衡被打破，房水的成分、性状、产生和排出的量都会发生明显的变化，此时房水成分的分析对临床诊断与治疗都有重要的意义。目前房水的检测主要通过前房穿刺抽取房水送检的方法来进行，但是不足之处在于：有创，抽取后伤口开放，因而有潜在的感染、组织损伤等风险，且对前房解剖结构和生理屏障都有影响；无法自主配合的儿童和成人无法获得样本；样本量极小，一般为0.05～0.15毫升，许多检测受限无法进行；无法短时间多次重复。

近年来，随着光学制造和加工技术的提高，互联网技术的应用，无创检测技术得到飞速发展，目前无创检测主要集中于釆用光学手段，光通常被用来传输信息，非接触式测量技术具有没有痛感、迅速、便捷和高灵敏度等优点。光学测量的手段主要有光声光谱法、拉曼光谱法、荧光法、偏振法、光学相干层析成像法、中红外法和近红外法等。近红外光谱分析技术探测的部位通常是人体皮肤、耳垂或含液体的组织。一般流程为：光源汇聚于探测的表面，经待测面反射或透射后直接探测光强，经校正模型建模后预测待测样品的浓度。在上世纪的80年代，近红外光谱分析技术开始应用于人体人体组织液葡萄糖浓度测量。

虽然近红外光谱分析技术用于房水测量在理论上是可行的，并且该技术在房水测量领域具有很大的优势，但是，其数学校正模型的精度较低和稳定性较差；光谱仪釆集到的近红外光谱通常会出现谱峰重叠的现象，这是由于分子的基团具有多样性造成的，同时探测到的光谱信号往往十份微弱，这是受到了其他生物组织成分的背景干扰影响；另外，房水中各个组分的浓度本身就很低，再加上背景光、分光系统、光纤探头和待测部分的外界情况及温度的影响，导致信号较弱。因此，数学校正模型的精度较低和稳定性较差、背景干扰及信号较弱等问题都会给房水组分浓度的预测带来了很大的误差和困难。

技术实现要素：

本发明的目的是提供一种近红外光无创测量人眼房水组分浓度的方法及系统，将近红外光谱分析技术应用于人眼房水的组分浓度测量，采用偏最小二乘法构建偏最小二乘法模型，并且对偏最小二乘法模型采用了波段优选方法来进行波段筛选，偏最小二乘法模型能够解决谱峰重叠的问题，而波段筛选则能够降低近红外光谱的背景干扰、提升处理效率且过滤弱信号，从而解决了目前房水组分检测有创、无法实时、连续检测的问题，提高了房水组分浓度的预测精度和稳定性。

本发明第一方面提供一种近红外光无创测量人眼房水组分浓度的方法，包括：

采集人眼房水样品校正集的校正近红外光谱数据及校正组分浓度数据；

根据校正近红外光谱数据及校正组分浓度数据，利用偏最小二乘法建立偏最小二乘法模型；

通过波段优选方法对偏最小二乘法模型的近红外光谱进行波段筛选，得到数学校正模型；

采集人眼房水待测样品的待测近红外光谱数据；

通过数学校正模型对待测近红外光谱数据进行组分浓度预测，得到人眼房水待测样品的组分浓度预测结果。

进一步的，根据校正近红外光谱数据及校正组分浓度数据，利用偏最小二乘法建立偏最小二乘法模型，包括：

对校正近红外光谱数据及校正组分浓度数据进行矩阵化处理，得到校正光谱矩阵及校正浓度矩阵；

利用偏最小二乘法，分别对校正光谱矩阵和校正浓度矩阵进行主成分运算，得到校正光谱矩阵及校正浓度矩阵的得分矩阵、载荷矩阵及残差矩阵；

根据得分矩阵、载荷矩阵及残差矩阵，进行多元线性回归处理，得到系数矩阵；

根据系数矩阵，构建得到偏最小二乘法模型。

进一步的，波段优选方法为组合移动区间偏最小二乘法，

通过波段优选方法对偏最小二乘法模型的近红外光谱进行波段筛选，得到数学校正模型，包括：

对校正近红外光谱数据进行预处理，得到近红外光谱的波长点及波长数；

根据组合移动区间偏最小二乘法，在近红外光谱的光谱区间中设置宽度可变的波长区间，最小波长区间的波长数为预先设置，从第一个起始波长点开始，依次向右移动一个波长点直到最后波长点，在每个波长点处，波长区间的大小由最小波长区间数依次增加到最大，且每次增加一个最小波长区间；

依次选取不同的起始波长点和波长区间，分别建立偏最小二乘法模型，得到不同的起始波长点和波长区间对应的局部预测模型；

对每一个局部预测模型均利用交叉有效性方法，确定最佳主成分数，得到不同的起始波长点和波长区间对应的局部最优预测模型；

比较局部最优预测模型，筛选出全局最优预测模型，作为数学校正模型。

进一步的，波段优选方法为改进遗传算法，

通过波段优选方法对偏最小二乘法模型的近红外光谱进行波段筛选，得到数学校正模型，包括：

对校正近红外光谱数据进行预处理，得到近红外光谱的波长点及波长数；

根据波长点及波长数，将近红外光谱分成多个等分区间，将每一个等分区间的波长点进行编码，得到每一个等分区间的基因；

建立初始群体，初始群体的个体数和基因长度为预先设定；

根据遗传算法，对基因进行复制、交叉和变异处理，直到最大繁殖，通过自适应函数判断每一个等分区间建立的偏最小二乘法模型，确定最优等分区间组合；

根据最优等分区间组合，建立最优偏最小二乘法模型，作为数学校正模型。

进一步的，方法还包括：

基于双隐层人工神经网络，构建数学校正模型的人工神经网络；

通过人工神经网络对数学校正模型进行迭代修正处理，使得数学校正模型的误差处于预期范围之内。

本发明第二方面提供一种近红外光无创测量人眼房水组分浓度的系统，包括：

数据采集模块，用于采集人眼房水样品校正集的校正近红外光谱数据及校正组分浓度数据；

基础模型构建模块，用于根据校正近红外光谱数据及校正组分浓度数据，利用偏最小二乘法建立偏最小二乘法模型；

优化模型构建模块，用于通过波段优选方法对偏最小二乘法模型的近红外光谱进行波段筛选，得到数学校正模型；

数据采集模块，还用于采集人眼房水待测样品的待测近红外光谱数据；

优化模型模块，用于通过数学校正模型对待测近红外光谱数据进行组分浓度预测，得到人眼房水待测样品的组分浓度预测结果。

进一步的，基础模型构建模块包括：

矩阵化处理单元，用于对校正近红外光谱数据及校正组分浓度数据进行矩阵化处理，得到校正光谱矩阵及校正浓度矩阵；

主成分运算单元，用于利用偏最小二乘法，分别对校正光谱矩阵和校正浓度矩阵进行主成分运算，得到校正光谱矩阵及校正浓度矩阵的得分矩阵、载荷矩阵及残差矩阵；

多元线性回归单元，用于根据得分矩阵、载荷矩阵及残差矩阵，进行多元线性回归处理，得到系数矩阵；

基础模型构建单元，用于根据系数矩阵，构建得到偏最小二乘法模型。

进一步的，波段优选方法为组合移动区间偏最小二乘法，

优化模型构建模块包括：

光谱预处理单元，用于对校正近红外光谱数据进行预处理，得到近红外光谱的波长点及波长数；

波长区间设置单元，用于根据组合移动区间偏最小二乘法，在近红外光谱的光谱区间中设置宽度可变的波长区间，最小波长区间的波长数为预先设置，从第一个起始波长点开始，依次向右移动一个波长点直到最后波长点，在每个波长点处，波长区间的大小由最小波长区间数依次增加到最大，且每次增加一个最小波长区间；

优化模型构建单元，用于依次选取不同的起始波长点和波长区间，分别建立偏最小二乘法模型，得到不同的起始波长点和波长区间对应的局部预测模型；

优化模型构建单元，还用于对每一个局部预测模型均利用交叉有效性方法，确定最佳主成分数，得到不同的起始波长点和波长区间对应的局部最优预测模型；

优化模型构建单元，还用于比较局部最优预测模型，筛选出全局最优预测模型，作为数学校正模型。

进一步的，波段优选方法为改进遗传算法，

优化模型构建模块包括：

光谱预处理单元，用于对校正近红外光谱数据进行预处理，得到近红外光谱的波长点及波长数；

波长区间设置单元，用于根据波长点及波长数，将近红外光谱分成多个等分区间，将每一个等分区间的波长点进行编码，得到每一个等分区间的基因；

优化模型构建单元，用于建立初始群体，初始群体的个体数和基因长度为预先设定；

优化模型构建单元，还用于根据遗传算法，对基因进行复制、交叉和变异处理，直到最大繁殖，通过自适应函数判断每一个等分区间建立的偏最小二乘法模型，确定最优等分区间组合；

优化模型构建单元，还用于根据最优等分区间组合，建立最优偏最小二乘法模型，作为数学校正模型。

进一步的，系统还包括：人工神经网络模块；

人工神经网络模块，用于基于双隐层人工神经网络，构建数学校正模型的人工神经网络；

人工神经网络模块，还用于通过人工神经网络对数学校正模型进行迭代修正处理，使得数学校正模型的误差处于预期范围之内。

由上可见，本发明中先采集人眼房水样品校正集的校正近红外光谱数据及校正组分浓度数据，根据校正近红外光谱数据及校正组分浓度数据，利用偏最小二乘法建立偏最小二乘法模型，通过波段优选方法对偏最小二乘法模型的近红外光谱进行波段筛选，得到数学校正模型，采集人眼房水待测样品的待测近红外光谱数据，通过数学校正模型对待测近红外光谱数据进行组分浓度预测，得到人眼房水待测样品的组分浓度预测结果。与现有的近红外光谱分析技术相比，本发明将近红外光谱分析技术应用于人眼房水的组分浓度测量，采用偏最小二乘法构建偏最小二乘法模型，并且对偏最小二乘法模型采用了波段优选方法来进行波段筛选，偏最小二乘法模型能够解决谱峰重叠的问题，而波段筛选则能够降低近红外光谱的背景干扰、提升处理效率且过滤弱信号，从而解决了目前房水组分检测有创、无法实时、连续检测的问题，提高了房水组分浓度的预测精度和稳定性。

附图说明

为了更清楚地说明本发明实施例中的技术方案，下面将对现有技术和实施例中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

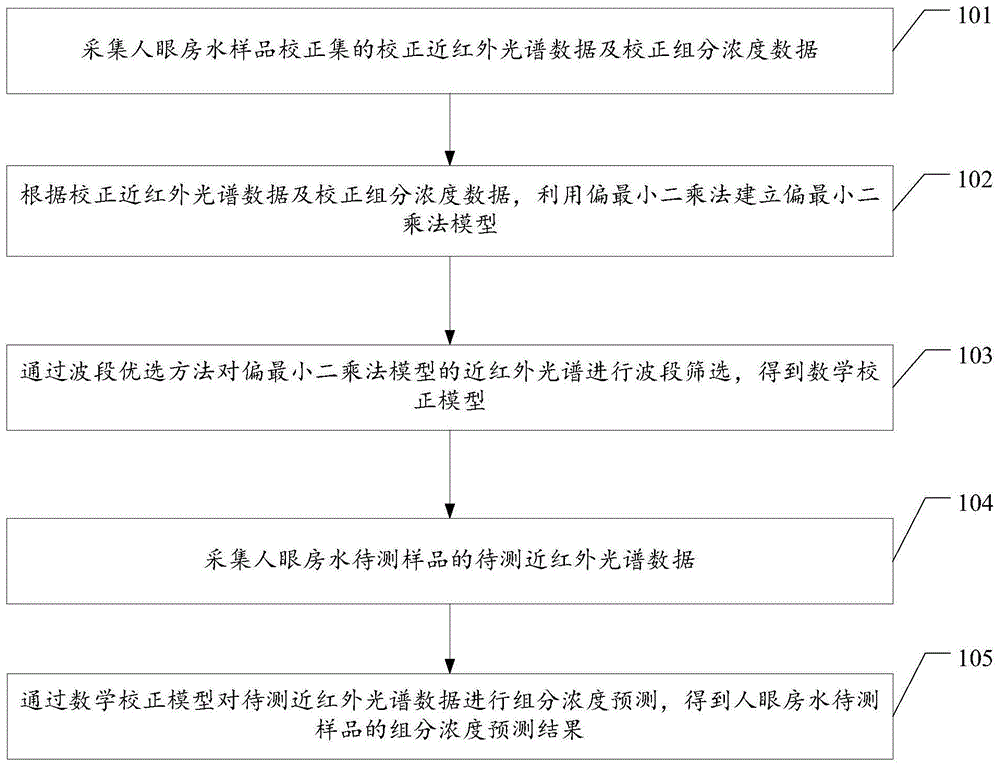
图1为本发明提供的近红外光无创测量人眼房水组分浓度的方法的一个实施例的流程示意图；

图2为本发明提供的人眼剖面图；

图3为本发明提供的近红外光无创测量人眼房水组分浓度的方法的另一个实施例的流程示意图；

图4为本发明提供的采用组合移动区间偏最小二乘法进行波段筛选的流程示意图；

图5为本发明提供的采用改进遗传算法进行波段筛选的流程示意图；

图6为本发明提供的近红外光无创测量人眼房水组分浓度的系统的一个实施例的结构示意图；

图7为本发明提供的近红外光无创测量人眼房水组分浓度的系统的另一个实施例的结构示意图；

图8为本发明提供的近红外光无创测量人眼房水组分浓度的系统的又一个实施例的结构示意图；

图9为本发明提供的近红外光无创测量人眼房水组分浓度的系统的再一个实施例的结构示意图；

图10为本发明提供的近红外光无创测量人眼房水组分浓度的系统的又一个实施例的结构示意图。

具体实施方式

本发明的核心是提供一种近红外光无创测量人眼房水组分浓度的方法及系统，将近红外光谱分析技术应用于人眼房水的组分浓度测量，采用偏最小二乘法构建偏最小二乘法模型，并且对偏最小二乘法模型采用了波段优选方法来进行波段筛选，偏最小二乘法模型能够解决谱峰重叠的问题，而波段筛选则能够降低近红外光谱的背景干扰、提升处理效率且过滤弱信号，从而解决了目前房水组分检测有创、无法实时、连续检测的问题，提高了房水组分浓度的预测精度和稳定性。

为使本发明实施例的目的、技术方案和优点更加清楚，下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

如图1所示，本发明实施例提供一种近红外光无创测量人眼房水组分浓度的方法，包括：

101、采集人眼房水样品校正集的校正近红外光谱数据及校正组分浓度数据；

本实施例中，人眼是人体视觉系统的组成部分，呈椭球状，其剖面图如图2所示。其中角膜和虹膜之间的空间为前房，里面充盈着房水。前房位于人眼角膜和晶状体之间，正常深度为3.13土0.50mm，其中充满无色透明的房水，正常情况下其组分、温度、理化与光学特性均十分稳定，为眼内结构如晶状体、视网膜的正常生理功能提供保障，且与人体组织液及其他组织液有较高关联性。糖尿病视网膜病变是糖尿病最早出现的微血管病变部位之一，因此房水中的葡萄糖及其他病理生理组分检测，可能较好、较早、无创地反映血糖及糖尿病眼部病变的情况。为晶状体提供营养以及排除角膜的中间代谢产物。房水成分单纯，且其中的葡萄糖浓度与人体组织液中的葡萄糖浓度具有较高的关联性，其他组分同样与人体组织液成分具有关联性，因此选择房水作为检测部位将提高近红外检测的预测能力。此外，临床调查表明，糖尿病的早期症状会出现在人眼中，因此前房房水中的葡萄糖浓度能够较早地准确反映血糖的浓度，从而实现糖尿病的早期诊断。其他病变及前兆也在房水组分的变化中有所体现。为了测量人眼前房水中的各个组分的含量，从光学采集方法上分析可以采取以下二种物理模型：直射模型：近红外光源垂直瞳孔射入光线宽度小于瞳孔直径的平行光线，通过视网膜反射/散射，再用光纤探头接收。反射/散射光谱信号包含房水、晶状体以及视网膜成分的信息，会产生较多的噪声，对葡萄糖浓度分析产生较大的干扰；斜射模型：将近红外光源斜入射人眼，经房水照射在晶状体表面，在晶状体表面产生反射，再经房水和角膜射出，然后通过光纤注入采集器，通过光谱仪分出射光的光谱数据。

由于斜射模型中反射的近红外光包含的光谱信号较为纯净，所以斜射模型是较好的选择。本发明实施例中采取斜射模型进行研究。

近红外光谱分析技术进行人体葡萄糖浓度的测量的原理为当射入的近红外光被葡萄糖吸，探测器接收到的透射光随葡萄糖溶液的浓度增加，其透射光谱在近红外波段内的吸光度也跟着增加，并呈线性关系。根据此原理，在对房水主要组分进行测量时，将测试光谱数据和已知样品的浓度数据建立一个数学校正模型，基于此数学校正模型，釆集未知浓度的待测样品数据并分析其浓度。近红外光谱分析技术并不是直接测量房水组分浓度，而是通过校正模型来间接的测量。此数学模型的建立需要研究近红外光谱分析和化学计量学中的多元线性回归法在房水组分浓度测量中的应用，其中的关键在于建立预测精度高和稳定性好的数学校正模型。近红外光的波长范围约为800nm～2500nm,通常是指波长介于可见光与中红外之间的电磁波。近红外光谱定量分析技术是指利用待测物体对近红外光的吸收来进行定性和定量分析的一种间接分析技术。

选择足够多的有代表性的人眼房水样品作为人眼房水样品校正集，并测量其近红外光谱曲线，得到校正近红外光谱数据。由于人眼房水样品校正集包含的数据越多，建立的数学校正模型的预测性和抗干扰能力就会越好，因此，人眼房水样品校正集的样品量越多越好。而人眼房水样品校正集中的样品的校正组分浓度数据可以是通过预先测量或者在预先制备时就确定的。

102、根据校正近红外光谱数据及校正组分浓度数据，利用偏最小二乘法建立偏最小二乘法模型；

本实施例中，近红外光谱分析技术的理论基础是比尔朗伯(lambert-beer)定律，当人眼房水样品吸收近红外光后，釆集到的校正近红外光谱数据中的吸光度与浓度成正比，即符合lambert-beer定律：

其中，aλ为样品的近红外光吸光度；i0与i分别为入射光和透射光的光强；ε为样品在某个波长下的吸光系数，它是波长的函数；l为通过样品的光程长；c为吸收物的浓度。

如果己知ε和l，根据实测的aλ，求得浓度c：

当待测样品中含有多种成分，结果仍然满足比尔-朗伯定律，在待测样品的组成成分的浓度与其吸光度之间就建立了线性关系。其数学表达式如下：

其中，εi为第i种的组成成分在特定波长处的吸收系数，ci为对应组成成分的浓度。对于给定的某种组成成分，其吸收系数为常数。待测样品中某种组成成分的浓度发生变化时，就会导致吸光度的变化。通过对待测样品浓度和吸光度进行线性关联，建立就能够建立模型，从而能够通过某未知样品的吸光度曲线和模型来预测其浓度。

化学计量学通常用于处理多变量模型，其中应用最多的就是多元线性回归法。当待测样品含有多种组成成分时，在进行近红外光谱测量时，探测器所获得的光谱信号是样品所有成分对近红外光的吸收，即是比尔朗伯具有叠加的特点，该特点的表达式如下：

对于n个样本，每个样本包含p个组成成分，在m个波长下测量待测样本的光谱数据，其光谱数据可以用一个nxp阶矩阵表示为：

其中，cij表示第i个待测样本的第j个组分的浓度所测得的吸光度，所测得的吸光度用下面矩阵表示：

其中，aij表示第i个待测样本的第j个波长下测得的吸光度值。根据比尔朗伯定律和叠加定律有：

am×n＝bm×p×cp×m+em×n

其中，em×n表示测量误。

采用变换：x＝at，y＝ct，b＝bt，e＝et，则有：

xn×m＝yn×p×bp×m+en×m

这就是多成分的模型，展开如下:

式中，xij表示在第i个待测样本的第j个波长处测得的数据，yik是第i个待测样本中第k个组分的浓度数据，bkj是第k个组分在第j个波长处的系数，eij表示第i个待测样本的第j个波长处的测量误差。

浓度和吸光度具有对应关系，为了便于研究以及数据处理，根据以上模型转换，建立如下函数关系：

即：

yn×p＝xn×m×bm×p+en×p

在以上近红外光谱分析技术的原理和思路的基础上，本实施例中，采用偏最小二乘法将主成分提取和多元线性回归相结合的方式，建立偏最小二乘法模型。

103、通过波段优选方法对偏最小二乘法模型的近红外光谱进行波段筛选，得到数学校正模型；

本实施例中，在得到偏最小二乘法模型之后，通过波段优选方法对偏最小二乘法模型的近红外光谱进行波段筛选，波段优选方法可以是组合移动区间偏最小二乘法或者是改进遗传算法，通过波段筛选，可以减少模型的数据处理量，提高效率，而且可以降低背景的干扰，提到精度和稳定性。

104、采集人眼房水待测样品的待测近红外光谱数据；

本实施例中，在数学校正模型构建完成之后，采集人眼房水待测样品的待测近红外光谱数据。

105、通过数学校正模型对待测近红外光谱数据进行组分浓度预测，得到人眼房水待测样品的组分浓度预测结果。

本实施例中，将待测近红外光谱数据作为数学校正模型的输入，数学校正模型依据待测近红外光谱数据，进行组分浓度预测，得到人眼房水待测样品的组分浓度预测结果，从而实现人眼房水的组分浓度预测。

本发明实施例中，将近红外光谱分析技术应用于人眼房水的组分浓度测量，采用偏最小二乘法构建偏最小二乘法模型，并且对偏最小二乘法模型采用了波段优选方法来进行波段筛选，偏最小二乘法模型能够解决谱峰重叠的问题，而波段筛选则能够降低近红外光谱的背景干扰、提升处理效率且过滤弱信号，从而解决了目前房水组分检测有创、无法实时、连续检测的问题，提高了房水组分浓度的预测精度和稳定性。

在以上图1所示的实施例中，利用偏最小二乘法建立偏最小二乘法模型，以及通过波段优选方法对偏最小二乘法模型的近红外光谱进行波段筛选都未进行具体说明，下面通过图3所示的实施例进行详细说明。

如图3所示，本发明实施例提供一种近红外光无创测量人眼房水组分浓度的方法，包括：

301、采集人眼房水样品校正集的校正近红外光谱数据及校正组分浓度数据；

详情请参考图1实施例中的步骤101；

302、对校正近红外光谱数据及校正组分浓度数据进行矩阵化处理，得到校正光谱矩阵及校正浓度矩阵；

本实施例中，假设校正近红外光谱测量的时候有p个自变量，表示为x1，x2，…，xp，校正组分浓度有q个因变量，表示为y1，y2，…，yq，试验测得的数据均为n个，校正光谱矩阵通过吸光度矩阵x(自变量矩阵)表示，x和校正浓度矩阵y(因变量矩阵)表示为：

303、利用偏最小二乘法，分别对校正光谱矩阵和校正浓度矩阵进行主成分运算，得到校正光谱矩阵及校正浓度矩阵的得分矩阵、载荷矩阵及残差矩阵；

本实施例中，现有的多元线性回归法是在因变量和自变量之间建立直接关系。因变量yi为浓度变量，样本个数为n，自变量xij为吸光度变量，对因变量和自变量建立线性方程组：

表示成矩阵形式为：

y＝x×b+e

对于该数学模型的解有三种情况：

当m＞n时，即因变量和自变量的个数大于样本的个数时，系数矩阵有无穷解；

当m＝n时，如果自变量矩阵满秩时，系数矩阵有惟一的解，实际应用里很难发生；

当m＜n时，即因变量和自变量个数小于样本个数时，此时系数矩阵没有准确的解，但是可以通过计算残差，使得其尽可能无穷小而得到最好的结果，即最小二乘法：

b＝(x^tx)^-1x^ty

如果因变量的个数为p，那么对因变量和自变量建立nxp个线性方程组：

yn×p＝xn×m×bm×p+en×p

但是，多元线性回归法的缺点为：获得样品的光谱数据往往成线性比例，这样就会产生共线性的问题，从而导致光谱数据不满秩，就不能用对光谱矩阵进行求逆m。另外在建立数学校正模型时，光谱数据中还含有其他物质或者噪声的浓度信息，如果使用了这些浓度信息建模，就会产生过度拟合的情况，从而影响到校正模型的实际预测能力。

因此，本发明实施例中偏最小二乘法将主成分运算和多元线性回归法结合的方式：主成分多元线性回归法是基于主成分提取的一种多元线性回归方法，其核心路线是将光谱数据进行降维，以消除光谱相互重叠的部分。主成分回归过程中会产生新的变量，这些变量能够在尽可能表征原变量特征的情况下，降低自身的维度，从而减少数据量的计算，所以，以主成分运算为基础不仅能够有效解决数据繁冗的问题，还能够解决多元线性回归法中产生的光谱数据共线问题，同时在一定程度上还消除背景噪声干扰。由于这些新的变量是相互正交的，使用它们进行多元线性回归建模时，就不会出现共线性的问题。另外各个新的变量能够尽可能的代表原始变量，成功的排除吸收光谱中包含的对模型不利的噪声影响，筛选出与浓度有关的变量参加线性回归。

主成分运算具体过程为：

将x矩阵和y矩阵进行主成分运算，得到如下表达式：

x＝tp^t+e；

y＝uq^t+f。

其中t矩阵是校正光谱矩阵的得分矩阵，p矩阵是校正光谱矩阵的载荷矩阵，e矩阵是校正光谱矩阵的残差矩阵，u矩阵是校正浓度矩阵的得分矩阵，q矩阵是校正浓度矩阵的载荷矩阵。f矩阵是校正浓度矩阵的残差矩阵。

304、根据得分矩阵、载荷矩阵及残差矩阵，进行多元线性回归处理，得到系数矩阵；

本实施例中，在计算得到得分矩阵、载荷矩阵及残差矩阵之后，进行多元线性回归处理，得到系数矩阵b，计算方式为：

u＝tb；

b＝(t^tt)^-1t^tu。

305、根据系数矩阵，构建得到偏最小二乘法模型；

本实施例中，在计算得到系数矩阵b之后，构建偏最小二乘法模型，构建方式如下：

假设，人眼房水待测样品的得分矩阵ti是通过待测样品的吸光度矩阵xi和求的p矩阵得到，然后得到待测样品的组分浓度矩阵yi，表达式如下：

yi＝tibq。

306、通过波段优选方法对偏最小二乘法模型的近红外光谱进行波段筛选，得到数学校正模型；

本实施例中，由于近红外光谱存在谱带重叠、信号较弱和光谱波长点大量冗余等问题，使得全谱段的模型建立通常会受到一些无关变量的影响，导致预测模型维度大且精度低，因此，需要进行波段筛选，以降低预测模型维度并提高其预测精度。波段优选方法可以包括组合移动区间偏最小二乘法或者改进遗传算法，下面针对每一种方法分别进行说明，具体如下：

(一)、波段优选方法为组合移动区间偏最小二乘法；

现有的间隔偏最小二乘法：将测得的光谱等分为w个等宽的波段区间，把每个波段区间内连续的w个波长点作为一个区间，设置最大主成分数，对每一个区间利用偏最小二乘法建立预测模型，根据模型评价找出对应每一波段区间的最佳主成分数，最后通过对比每个区间的最佳预测模型，找出目标光谱信息含量最多的建模区间；

现有的区间移动偏最小二乘法：选取含有m个波长点的区间，从采集的近红外光谱(假设有μ个波长点)中的第一个波长点开始依次向右移动一个波长点直至最后。落在区间内的波长点为i到(i+m-1)，其中i为区间起始波长点，m为区间宽度，从而可以从整个光谱中依次选择(μ-m+1)个包含m个波长点的子波长区，设置最大主成分数，对每一个区间利用偏最小二乘法建立预测模型，根据模型预测结果找出对应每一波段区间的最佳主成分数，最后通过对比每个区间的预测结果，筛选出最适合建模的波段。

但是，间隔偏最小二乘法和区间移动偏最小二乘法都是直接设置最大主成分数，并不能保证每个子预测模型的预测误差达到最小，从而影响模型的预测精度和稳定性，无法筛选出最合适的建模波段。因此，本发明实施例中，采用组合移动区间偏最小二乘法，具体过程如图4所示：

401、对校正近红外光谱数据进行预处理，得到近红外光谱的波长点及波长数；

402、根据组合移动区间偏最小二乘法，在近红外光谱的光谱区间中设置宽度可变的波长区间，最小波长区间的波长数为预先设置，从第一个起始波长点开始，依次向右移动一个波长点直到最后波长点，在每个波长点处，波长区间的大小由最小波长区间数依次增加到最大，且每次增加一个最小波长区间；

403、依次选取不同的起始波长点和波长区间，分别建立偏最小二乘法模型，得到不同的起始波长点和波长区间对应的局部预测模型；

404、对每一个局部预测模型均利用交叉有效性方法，确定最佳主成分数，得到不同的起始波长点和波长区间对应的局部最优预测模型；

405、比较局部最优预测模型，筛选出全局最优预测模型，作为数学校正模型。

(二)、波段优选方法为改进遗传算法。

遗传算法是利用大自然中的优胜劣汰而发展起来的随机全局搜索和优化方法，遗传算法本质上是一种快速、高能和大范围搜寻的手段。它能在大范围的搜寻中自动获得所需要的信息，并自动的进行优胜劣汰式的筛选出最优解。遗传算法的原理是大自然的优胜劣汰原则，通过大范围的全局搜索来产生一个近似的最优解的方案。在遗传算法的每一次筛选中，根据个体的适应度和从大自然中借鉴来的优胜劣汰进行大范围筛选，从而产生最优解。这个过程让每个个体得到进化，得到的新个体比原个体适应度更强，就像自然界中的进化一样。

遗传算法属于随机的全局搜寻算法，它是基于编码技术，以染色体的方式模拟这些个体的优胜劣汰过程。通过大范围的、随机的搜寻来寻找那些适应值高的个体，从而实现波段的筛选。

但是，现有的遗传算法都是选择独立的单个波长进行波段筛选，建模波长之间往往相关性较差，从而导致模型的稳定性较差。因此，本发明实施例中，采用改进遗传算法，具体过程如图5所示：

501、对校正近红外光谱数据进行预处理，得到近红外光谱的波长点及波长数；

502、根据波长点及波长数，将近红外光谱分成多个等分区间，将每一个等分区间的波长点进行编码，得到每一个等分区间的基因；

503、建立初始群体，初始群体的个体数和基因长度为预先设定；

504、根据遗传算法，对基因进行复制、交叉和变异处理，直到最大繁殖，通过自适应函数判断每一个等分区间建立的偏最小二乘法模型，确定最优等分区间组合；

505、根据最优等分区间组合，建立最优偏最小二乘法模型，作为数学校正模型。

本发明实施例中，详细的介绍了利用偏最小二乘法建立偏最小二乘法模型的具体过程，能够解决现有的多元线性回归法存在的谱带重叠的问题；对波段优选方法具体是组合移动区间偏最小二乘法和改进遗传算法的情况进行了详细的描述，波段筛选能够降低近红外光谱的背景干扰、提升处理效率且过滤弱信号。

在以上图1和图3所示的实施例的基础上，为了提高数学校正模型的预测准确性，还需要增加人工神经网络进行优化，可选的，近红外光测量人眼房水组分浓度的方法还包括：

基于双隐层人工神经网络，构建数学校正模型的人工神经网络；

通过人工神经网络对数学校正模型进行迭代修正处理，使得数学校正模型的误差处于预期范围之内。

本发明实施例中，人工神经网络是一种仿照生物神经网络结构和功能的计算模型。神经网络由大量的神经元(节点)连接而成，每个神经元具有一种特定的输出函数，称为激励函数，每两个神经元间的连接都代表一个对于通过该连接信号的加权值，称之为权重。选择适合的激励函数，神经网络可以是一个高度复杂的非线性系统，具有自组织、自适应和自学习能力，特别适合处理多变量复杂的信息处理问题，因此常常用于探索复杂变量间的内部联系。神经元是一个多输入单输出的非线性信息处理单元；

由于房水成分含量和光谱之间不是简单的线性关系，s型函数的输出是非线性的，常将这种激励函数的神经元称为非线性连续型模型，因此适合选用s型函数作为隐层每个节点的激励函数，输出节点采用线性型激励函数，将采集到的数据作为人工神经网络的输入，采用神经网络进行深度学习，可以实现系统持续优化；

由于人工神经网络是一种按误差反向传播算法训练的多层前馈网络，是目前应用最广的神经网络模型之一。它的学习规则是使用最速下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小，从而达到训练的目标。本实施例中选用的都是双隐层人工神经网络结构。通过对不同层数和神经元数进行反复大量的建模，比较建模效果和交叉验证精度，以确定神经网络最佳参数；

当神经网络正向传播时，输入信息通过输入层经两级隐含层处理后传向输出层，每一层神经元特性只影响下一层的神经元状态。如果在输出层得到的结果不满足建模停止条件，则转入反向传播，将误差信号沿原来的神经元通路逆向传播。返回过程中，逐一修改连接各层神经元的权值和阈值，上述过程不断迭代修正，最后使得建模误差处于预期范围之内，预期范围是按照模型的允许范围而设置的。

在以上的实施例中，具体介绍了近红外光测量人眼房水组分浓度的方法，下面通过实施例对应用该方法的近红外光测量人眼房水组分浓度的系统进行说明。

如图6所示，本发明实施例提供一种近红外光无创测量人眼房水组分浓度的系统，包括：

数据采集模块601，用于采集人眼房水样品校正集的校正近红外光谱数据及校正组分浓度数据；

基础模型构建模块602，用于根据校正近红外光谱数据及校正组分浓度数据，利用偏最小二乘法建立偏最小二乘法模型；

优化模型构建模块603，用于通过波段优选方法对偏最小二乘法模型的近红外光谱进行波段筛选，得到数学校正模型；

数据采集模块601，还用于采集人眼房水待测样品的待测近红外光谱数据；

优化模型模块604，用于通过数学校正模型对待测近红外光谱数据进行组分浓度预测，得到人眼房水待测样品的组分浓度预测结果。

本发明实施例中，数据采集模块601采集人眼房水样品校正集的校正近红外光谱数据及校正组分浓度数据，基础模型构建模块602根据校正近红外光谱数据及校正组分浓度数据，利用偏最小二乘法建立偏最小二乘法模型，优化模型构建模块603通过波段优选方法对偏最小二乘法模型的近红外光谱进行波段筛选，得到数学校正模型，数据采集模块604采集人眼房水待测样品的待测近红外光谱数据，优化模型模块605通过数学校正模型对待测近红外光谱数据进行组分浓度预测，得到人眼房水待测样品的组分浓度预测结果。与现有的近红外光谱分析技术相比，本发明将近红外光谱分析技术应用于人眼房水的组分浓度测量，采用偏最小二乘法构建偏最小二乘法模型，并且对偏最小二乘法模型采用了波段优选方法来进行波段筛选，偏最小二乘法模型能够解决谱峰重叠的问题，而波段筛选则能够降低近红外光谱的背景干扰、提升处理效率且过滤弱信号，从而解决了目前房水组分检测有创、无法实时、连续检测的问题，提高了房水组分浓度的预测精度和稳定性。

结合图6所示的实施例，可选的，如图7所示，本发明的一些实施例中，基础模型构建模块602包括：

矩阵化处理单元701，用于对校正近红外光谱数据及校正组分浓度数据进行矩阵化处理，得到校正光谱矩阵及校正浓度矩阵；

主成分运算单元702，用于利用偏最小二乘法，分别对校正光谱矩阵和校正浓度矩阵进行主成分运算，得到校正光谱矩阵及校正浓度矩阵的得分矩阵、载荷矩阵及残差矩阵；

多元线性回归单元703，用于根据得分矩阵、载荷矩阵及残差矩阵，进行多元线性回归处理，得到系数矩阵；

基础模型构建单元704，用于根据系数矩阵，构建得到偏最小二乘法模型。

本发明实施例中，详细的介绍了基础模型构建模块602利用偏最小二乘法建立偏最小二乘法模型的具体过程，能够解决现有的多元线性回归法存在的谱带重叠的问题。

结合图7所示的实施例，可选的，如图8所示，本发明的一些实施例中，波段优选方法为组合移动区间偏最小二乘法，

优化模型构建模块603包括：

光谱预处理单元801，用于对校正近红外光谱数据进行预处理，得到近红外光谱的波长点及波长数；

波长区间设置单元802，用于根据组合移动区间偏最小二乘法，在近红外光谱的光谱区间中设置宽度可变的波长区间，最小波长区间的波长数为预先设置，从第一个起始波长点开始，依次向右移动一个波长点直到最后波长点，在每个波长点处，波长区间的大小由最小波长区间数依次增加到最大，且每次增加一个最小波长区间；

优化模型构建单元803，用于依次选取不同的起始波长点和波长区间，分别建立偏最小二乘法模型，得到不同的起始波长点和波长区间对应的局部预测模型；

优化模型构建单元803，还用于对每一个局部预测模型均利用交叉有效性方法，确定最佳主成分数，得到不同的起始波长点和波长区间对应的局部最优预测模型；

优化模型构建单元803，还用于比较局部最优预测模型，筛选出全局最优预测模型，作为数学校正模型。

本发明实施例中，对波段优选方法具体是组合移动区间偏最小二乘法的情况进行了详细的描述，利用组合移动区间偏最小二乘法的波段筛选能够降低近红外光谱的背景干扰、提升处理效率且过滤弱信号。

结合图7所示的实施例，可选的，如图9所示，本发明的一些实施例中，波段优选方法为改进遗传算法，

优化模型构建模块603包括：

光谱预处理单元901，用于对校正近红外光谱数据进行预处理，得到近红外光谱的波长点及波长数；

波长区间设置单元902，用于根据波长点及波长数，将近红外光谱分成多个等分区间，将每一个等分区间的波长点进行编码，得到每一个等分区间的基因；

优化模型构建单元903，用于建立初始群体，初始群体的个体数和基因长度为预先设定；

优化模型构建单元903，还用于根据遗传算法，对基因进行复制、交叉和变异处理，直到最大繁殖，通过自适应函数判断每一个等分区间建立的偏最小二乘法模型，确定最优等分区间组合；

优化模型构建单元903，还用于根据最优等分区间组合，建立最优偏最小二乘法模型，作为数学校正模型。

本发明实施例中，对波段优选方法具体是改进遗传算法的情况进行了详细的描述，能够降低近红外光谱的背景干扰、提升处理效率且过滤弱信号。

结合图6所示的实施例，可选的，如图10所示，本发明的一些实施例中，系统还包括：人工神经网络模块1001；

人工神经网络模块1001，用于基于双隐层人工神经网络，构建数学校正模型的人工神经网络；

人工神经网络模块1001，还用于通过人工神经网络对数学校正模型进行迭代修正处理，使得数学校正模型的误差处于预期范围之内。

本发明实施例中，利用基于双隐层人工神经网络的技术，能够对数学校正模型进行迭代修正处理，从而提高数学校正模型的预测结果的准确性。

本说明书中各个实施例采用递进的方式描述，每个实施例重点说明的都是与其他实施例的不同之处，各个实施例之间相同相似部分互相参见即可。对于实施例公开的装置而言，由于其与实施例公开的方法相对应，所以描述的比较简单，相关之处参见方法部分说明即可。

还需要说明的是，术语“包括”、“包含”或者其任何其他变体意在涵盖非排他性的包含，从而使得包括一系列要素的过程、方法、物品或者设备不仅包括那些要素，而且还包括没有明确列出的其他要素，或者是还包括为这种过程、方法、物品或者设备所固有的要素。在没有更多限制的情况下，由语句“包括一个……”限定的要素，并不排除在包括该要素的过程、方法、物品或者设备中还存在另外的相同要素。

对所公开的实施例的上述说明，使本领域专业技术人员能够实现或使用本发明。对这些实施例的多种修改对本领域的专业技术人员来说将是显而易见的，本文中所定义的一般原理可以在不脱离本发明的精神或范围的情况下，在其他实施例中实现。因此，本发明将不会被限制于本文所示的这些实施例，而是要符合与本文所公开的原理和新颖特点相一致的最宽的范围。