一种基于个体警觉行为的双层网络病毒传播模型建立方法与流程

本发明涉及网络科学和病毒传播领域，特别是指一种考虑个体警觉行为的双层网络病毒传播模型。

背景技术：

近年来，流行病的传播一直是复杂网络领域的一个热门话题。不论是黑死病，还是西班牙流感，抑或是近些年的sars及甲型h1n1流感，流行病的传播对人类的生产生活产生了巨大的影响。现实生活中，流行病的传播过程中往往会伴随着其他的传播过程，如信息传播，关于流行病的信息可以通过大众媒体在朋友以及家人之间迅速扩散，改变人们对流行病传播的认识，同时，在了解到流行病的信息时，个体为了避免感染流行病，其行为也发生相应改变，如戴口罩、避免接触及服用药物等，这些行为在一定程度上可以抑制流行病的传播。因此，对于流行病传播与信息扩散相互影响的研究，具有非常重要的现实意义。

为了探索双层网络中信息扩散与流行病传播的相互作用，国内外的学者们从各个方向和角度，提出了许多双层网络模型。一部分的研究通常将意识和流行病之间的相互作用建模为多层网络中的两个相互竞争的传播过程，如同物理接触网络中流行病的传播过程一样，意识也会从有意识的个体传给其在信息网络上的无意识邻居，通过促使更多个体在信息网络中成为有意识地个体，从而采取预防行为以抑制流行病在物理接触网络中的传播。但是每个人在网络中往往具有不用的身份与性格，因此假设网络中的个体具有相同的特性并不能够完全模拟现实生活中个体的活动通常受其异质性的情况。因此，另一部分研究考虑了网络中不同节点邻居特征的异质性，根据节点邻居数量的多少来构建双层网络病毒与信息交互的模型。

以上研究假设所有个体在了解流行病传播所产生的信息后都会产生警觉意识，却忽视了不同个体的在行为选择上的异质性，即不同个体在了解到流行病相关的信息后会采取不同的行为来避免感染流行病或者维持网络功能正常运行。如在流行病的传播期间，一部分已知流行病信息的个体可能会提高自身警觉性，注意基本的健康防护或其他策略来保证自身的健康。而另一部分个体虽然已知病毒信息，但是由于日常工作以及社交上的需求，不会对周围节点产生警觉性，或者仅对某一类人群产生警觉性，主动切断与部分邻居的接触，从而避免自身被感染。

技术实现要素：

发明目的：为了更好地研究多重网络中的病毒传播，为抑制病毒的感染率，控制病毒传播规模，本发明提供一种基于个体警觉行为的双层网络病毒传播模型构建方法，本发明考虑到个体在面对病毒传播时接触行为的异质性，在模型中，个体在了解到流行病相关的信息时会以一定概率成为警觉个体，从而改变个体行为来规避被流行病感染的风险。基于个体行为的异质性，我们提出了两种由个体警觉性所引起的接触行为策略，以研究其对流行病传播的影响，更加符合实际情况的双层网络模型—基于个体警觉性的双层网络传播模型，属于多重复杂网络。

技术方案：为实现上述目的，本发明采用的技术方案为：

一种基于个体警觉行为的双层网络病毒传播模型构建方法，包括以下步骤：

步骤1，获取流行病相关信息、信息传播相关参数以及个体警觉性参数。

步骤2，根据流行病相关参数、信息传播相关参数以及个体警觉性参数构建基础的信息扩散与流行病传播的双层网络模型，下层是描述流行病传播过程的物理接触网络层，上层是描述“流行病存在”信息传播的通信网络层，其中两层网络的节点表示同一个个体。

步骤3，在基础的信息扩散与流行病传播的双层网络模型中，下层物理接触网络层中的个体具有两种状态:易染状态s和感染状态i。在流行病传播过程中，当易染个体与感染个体相接触时，易染个体将以β的概率被感染；同时，感染个体以μ的概率恢复为易染个体。上层通信网络层中，个体具有两种形式:不了解信息的无意识状态u，以及了解信息的有意识状态a，在信息扩散的过程中，信息网络中了解信息的有意识个体每个时刻会向信息层中的邻居传播流行病相关的信息，在与无意识的邻居接触后会以概率λ使其变为有意识的个体，而有意识的个体会以δ的概率重新变为无意识个体，另外，物理接触网络层中无意识的感染个体在信息网络中会以概率κ转变为有意识状态，自发的向邻居节点传播流行病相关的信息。在流行病相关信息的传播过程中，接收到流行病相关信息的有意识个体则会采取适当地防护措施，以减少被流行病感染的风险，因此，若无意识的易感个体被流行病感染的概率为β，则有意识的易感个体被流行病感染的概率为σaβ，0≤σa≤1，σa表示有意识的易感个体被流行病感染系数。

步骤4，在此基础上考虑个体警觉性对于接触行为的影响，引入有意识个体产生警觉性v的概率a以及具有警觉性的个体恢复为非警觉状态r的概率b，其中a+b＝1。由此将基础的信息扩散与流行病传播的双层网络模型中的个体分为八类：不具有警觉性的无意识易感个体usr、不具有警觉性的无意识感染个体uir、不具有警觉性的有意识易感个体asr、不具有警觉性的有意识感染个体air、具有警觉性的无意识易感个体usv、具有警觉性的无意识感染个体uiv、具有警觉性的有意识易感个体asv以及具有警觉性的有意识感染个体aiv。基础的信息扩散与流行病传播的双层网络模型的微观马尔可夫过程的方程如下：

其中，分别为t时刻节点i处于usr、usv、asr、asv、uir、uiv、air以及aiv状态下的概率，并且满足归一化条件：

在上面的方程中，用cij和vij表示物理接触网络层和通信网络层的邻接矩阵元素，定义个体i不被任何邻居传播为知觉个体的概率为ri，在物理接触网络层，定义非警觉个体i在无意识状态时，不被任何邻居感染的概率为警觉个体i在无意识状态时，不被任何邻居感染的概率为同样，非警觉个体i在有意识状态时，不被任何邻居感染的概率为警觉个体i在有意识状态时，不被任何邻居感染的概率为于是有以下方程式：

其中，而ρ控制着两种应对方式的选取，ρ＝1时对应于采用个体警觉行为1，ρ＝0时对应于则采用个体警觉行为2。

优选的：步骤1中流行病相关信息由国家卫生部网站上公开的信息获取。信息传播相关参数通过爬取微博事件传播过程得到。个体警觉性参数由问卷调查得到。

优选的：步骤4中个体警觉行为1时，具有警觉性的个体会和同样具有警觉性的邻居个体保持物理接触，同时断开与非警觉邻居个体的物理接触，而不具有警觉性的个体则会和所有的邻居个体保持接触。

优选的：步骤4中个体警觉行为2时，具有警觉性的个体会和不具备警觉性的邻居个体保持物理接触，而断开与非警觉邻居个体的物理接触，而不具有警觉性的个体则会和所有的邻居个体保持接触。

本发明相比现有技术，具有以下有益效果：

本发明基于复杂网络中多层网络的信息扩散与流行病传播理论，引入了个体警觉性的概念，通过提出两种基于个体警觉性的接触行为模式，拓扑出更加贴合实际情况双层复杂网络传播模型，通过在ba-ba、ws-ws和ba-ws网络上的仿真并与不采用节点警觉性行为策略的情况对比，验证了本模型的有效性。

附图说明

图1是本发明的技术路线图。

图2是模型中各个节点状态转移概率树。

图3-a、图3-b、图3-c分别是在采取个体行为1时不同警觉性产生概率对最终的感染规模的影响情况。

图4-a、图4-b、图4-c分别是在采取个体行为2时不同警觉性产生概率对最终的感染规模的影响情况。

具体实施方式

下面结合附图和具体实施例，进一步阐明本发明，应理解这些实例仅用于说明本发明而不用于限制本发明的范围，在阅读了本发明之后，本领域技术人员对本发明的各种等价形式的修改均落于本申请所附权利要求所限定的范围。

一种基于个体警觉行为的双层网络病毒传播模型构建方法，如图1所示，包括以下步骤：

步骤1，获取流行病相关信息、信息传播相关参数以及个体警觉性参数。流行病相关信息由国家卫生部网站上公开的信息获取。信息传播相关参数通过爬取微博事件传播过程得到。个体警觉性参数由问卷调查得到。

步骤2，根据流行病相关参数、信息传播相关参数以及个体警觉性参数构建基础的信息扩散与流行病传播的双层网络模型，下层是描述流行病传播过程的物理接触网络层，上层是描述“流行病存在”信息传播的通信网络层，其中两层网络的节点表示同一个个体。

步骤3，在基础的信息扩散与流行病传播的双层网络模型中，如图2所示，下层物理接触网络层中的个体具有两种状态:易染状态(健康状态)s和感染状态i。在病毒传播过程中，当易染个体与感染个体相接触时，易染个体将以β的概率被感染；同时，感染个体以μ的概率恢复为易染个体。上层信息网络中，个体具有两种形式:不了解信息的无意识状态u，以及了解信息的有意识状态a。在信息扩散的过程中，信息网络中了解信息的有意识个体每个时刻会向信息层中的邻居传播流行病相关的信息，在与无意识的邻居接触后会以概率λ使其变为有意识的个体。同时，因为大多数流行病的传播都具有一定季节性或周期性，这就使得散播信息的有意识个体可能会遗忘流行病相关的信息或者不再传播，进而有意识的个体会以δ的概率重新变为无意识个体。另外，接触网络中无意识的感染个体在信息网络中会以概率κ转变为有意识状态，自发的向邻居节点传播流行病相关的信息。在流行病相关信息的传播过程中，接收到流行病相关信息的有意识个体则会采取适当地防护措施，以减少被流行病感染的风险，因此，若无意识的易感个体被流行病感染的概率为β，则有意识的易感个体被流行病感染的概率为σaβ(0≤σa≤1)，σa表示有意识的易感个体被流行病感染系数。

步骤4，在此基础上考虑个体警觉性对于接触行为的影响，引入有意识个体产生警觉性v的概率a以及具有警觉性的个体恢复为非警觉状态r的概率b，其中a+b＝1。由此将基础的信息扩散与流行病传播的双层网络模型中的个体分为八类：不具有警觉性的无意识易感个体usr、不具有警觉性的无意识感染个体uir、不具有警觉性的有意识易感个体asr、不具有警觉性的有意识感染个体air、具有警觉性的无意识易感个体usv、具有警觉性的无意识感染个体uiv、具有警觉性的有意识易感个体asv以及具有警觉性的有意识感染个体aiv。各个不同状态的个体之间的转换情况如附图2的状态转移概率树，根据节点的状态转移概率，我们给出了离散时间的微观马尔科夫方程，研究不同警觉性产生概率对流行病感染率的影响，基础的信息扩散与流行病传播的双层网络模型的微观马尔可夫过程的方程如下：

其中，分别为t时刻节点i处于usr、usv、asr、asv、uir、uiv、air以及aiv状态下的概率，并且满足归一化条件：

在上面的方程中，用cij和vij表示物理接触网络层和通信网络层的邻接矩阵元素，定义个体i不被任何邻居传播为知觉个体的概率为ri，在物理接触网络层，定义非警觉个体i在无意识状态时，不被任何邻居感染的概率为警觉个体i在无意识状态时，不被任何邻居感染的概率为同样，非警觉个体i在有意识状态时，不被任何邻居感染的概率为警觉个体i在有意识状态时，不被任何邻居感染的概率为于是有以下方程式：

其中，而ρ控制着两种应对方式的选取，ρ＝1时对应于采用个体警觉行为1，ρ＝0时对应于则采用个体警觉行为2。

个体警觉行为1时，具有警觉性的个体会和同样具有警觉性的邻居个体保持物理接触，同时断开与非警觉邻居个体的物理接触，而不具有警觉性的个体则会和所有的邻居个体保持接触。

个体警觉行为2时，具有警觉性的个体会和不具备警觉性的邻居个体保持物理接触，而断开与非警觉邻居个体的物理接触，而不具有警觉性的个体则会和所有的邻居个体保持接触。

建基础的双层传播模型如下：底层是演化流行病传播过程的物理接触网络，用sis病毒传播模型演化流行病的传播，上层是描述“病毒存在”信息传播的信息网络，用uau传播模型演化意识信息在信息网络中的传播，其中两层复杂网络的节点表示同一个个体。

多层网络中流行病与信息意识交互动力学的研究，需要考虑多层网络可能影响流行病传播的各个因素，在此基础上，更加全面的分析多层网络中的传播动力学，预测病毒传播规模，控制流行病的蔓延，我们分析选取不同个体行为以及不同产生警觉性的概率对多重网络传播动力学的影响:

我们选取了三种典型的双层网络模型进行了仿真实验：

首先是ba-ba多层网络，与下层的物理接触层相对应的网络采用无标度(ba)网络，节点数为2000，构造时每个节点在加入网络时与3个节点建立连接。与上层的信息传播层相对应的网络同为ba网络，上层表示信息传播的ba网络以下层的接触网络为基础，随机增加了400条边。

而对于ws-ws多层网络，与下层物理接触层相对应的网络采用小世界(ws)网络，节点数为2000，平均度<k>＝4。与上层信息传播层相对应的网络同为ws网络，上层表示信息传播的ws网络以下层的接触网络为基础，随机增加400条边。

最是ba-ws双层网络。与物理接触层相对应的网络采用无标度(ba)网络，节点数为2000，生成参数选取同之前的ba网络。与信息传播层相对应的网络为ws网络，节点数为2000，生成参数选取同之前的ws网络，上层信息扩散的ws网络我们依旧随机增加了400条边。

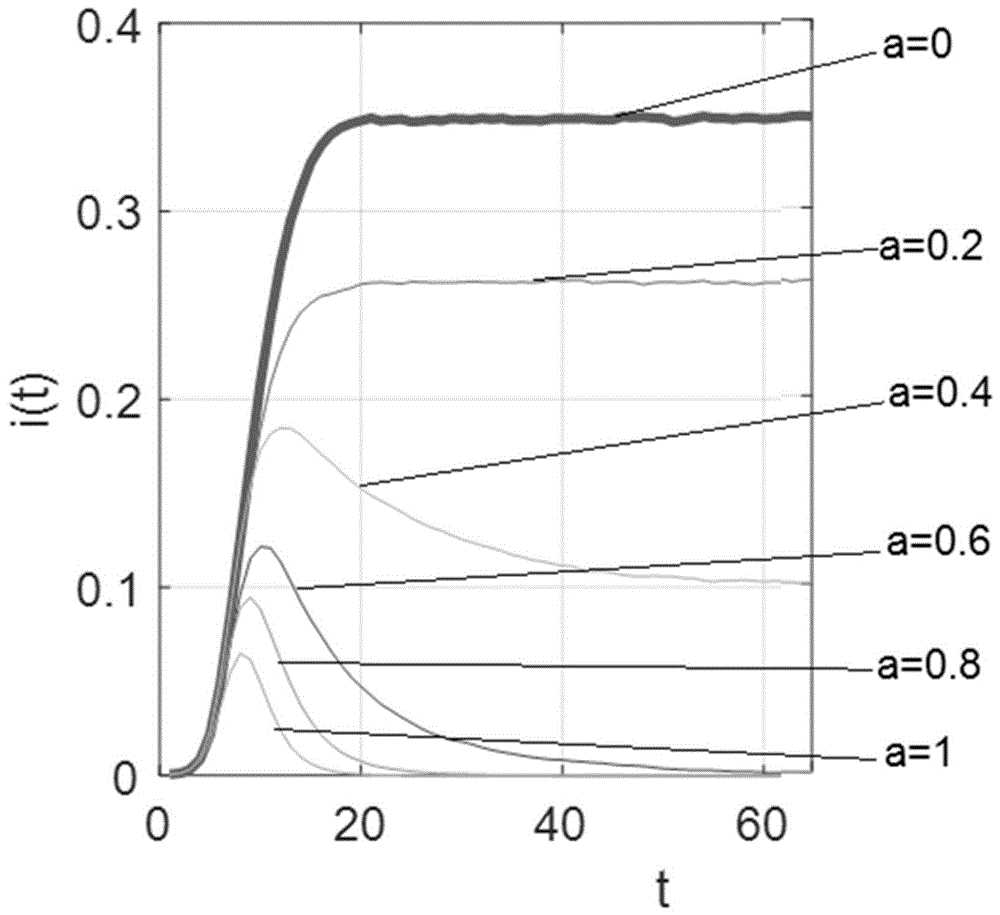
当选取个体行为1时，选取不同的a值在上文给出的三种双层网络中流行病感染率随时间的变化如图3所示。综合以图3-a、图3-b以及图3-c可以看出，当取较小的a值时个体行为1对于流行病的抑制作用较为明显，随着a取值的逐渐增大，个体行为1对于流行病的抑制作用会逐渐减弱。

从易感节点的角度出发，我们希望可以保护这些具有警觉性的易感节点，当其产生警觉性后通过调整接触行为策略，减小被流行病所感染的概率。通过使这些节点主动和同样具有警觉性的节点接触，可以切断与那些不具备警觉性的感染邻居节点的接触，于是在一定程度上可以减小其被流行病感染的概率。

一方面，当产生警觉性的概率a较小时，网络中只会有少部分有意识的节点处于警觉状态。其中具有警觉性的易感节点会切断与其他不具有警觉性的感染态邻居的接触，同时，网络中非警觉节点占大多数，其中包括大部分感染节点，因此这些具有警觉性的易感节点被感染的概率较低。另一方面，考虑到节点的意识一部分来源于信息的扩散，由与有意识的邻居通信所引发，另一部分来源于节点本身因感染流行病自发产生，因此有意识的节点中患病节点的比例会比无意识节点中患病节点的比例更高。当a的取值偏小时，不具备警觉性的易感节点比例高，通过采取个体行为1，也可以在一定程度上形成对具有警觉性节点的隔离，从而保护这些不具备警觉性的易感节点。因此，较小的值对流行病的抑制作用更明显。

随着有意识的节点产生警觉性概率a的增加，网络中警觉性恢复到非警觉性的概率会逐渐降低，最终网络中警觉节点的比例会逐渐增高，警觉性节点之间所组成的子网络会逐渐扩大，在其子网内部，子网中每个节点都会与其所有的邻居进行物理接触，于是个体行为1的效果会减弱。当a的取值为1时，网络中所有有意识的节点都会永久转变为警觉节点，此时警觉性节点所组成的子网络会扩展到几乎整个网络中，因此个体行为1会基本失效，其效果会接近不采取任何策略时的情况。而在不同的网络中，并不是所有的节点都有机会接收到关于流行病的信息，因此网络中会存在少数节点不具备警觉性，所以当a＝1与a＝0时的流行病感染率不会完全重合。

值得一提的是，当a的取值非常小时，网络中一开始警觉节点的比例也会非常小，在初期流行病感染率会基本和不采取策略时相接近，随着流行病在网络中的传播，警觉节点的比例随着有意识节点的数量增加而提高，此时个体行为1产生作用，使得流行病感染率逐渐下降，随着时间的推进感染率逐渐稳定，于是在初期流行病感染率会产生了一个峰值。

当选取个体行为2时，选取不同的a值在上文给出的三种双层网络中流行病感染率随时间的变化如图4所示。综合以图4-a、图4-b以及图4-c可以看出，当取较大的a值时个体行为2对于流行病的抑制作用较为明显，随着a取值的逐渐减小，个体行为2对于流行病的抑制作用逐渐减弱。

在采取个体行为2时，若从易感节点的角度考虑，具有警觉性的易感节点会选择与不具有警觉性的邻居接触，因为有意识的节点中有一部分节点的意识来源是因为其在物理接触网络中感染了流行病，与无意识的节点相比，有意识的节点中感染节点的比例会略高，因此通过避免与同样具有警觉性的节点的物理接触，个体被流行病感染的概率便会降低。

当a的取值偏小时，网络中只有小部分的有意识节点具备警觉性，因此具有警觉性的易感节点会主动与其非警觉邻居进行物理接触，其中包括了大部分感染节点，因此此时个体行为2对于流行病的抑制效果并不明显。

随着a的取值逐渐增大，有意识的节点中产生警觉性的概率会逐渐增大，考虑到有意识的节点中感染节点的比例较高，因此具有警觉性的易感节点通过改变接触行为，切断与同样是警觉状态的邻居的接触，从而能够有效的降低被流行病感染的风险。而当a取1时，网络中随着信息的扩散会有越来越多的节点永久地成为警觉节点，而警觉节点并不会主动与同样是警觉状态的邻居接触，因此当网络中警觉节点比例相当高时，网络中大部分连边都是处于被切断的状态，警觉节点之间相互孤立，网络基本不连通，此时流行病无法有效传播，随着感染个体的康复，流行病最终会在网络中消失。

而当a的取值较大时，考虑到前文提到有意识的个体中感染流行病的比例会略高，因此在初期，这些节点在产生警觉性后会通过与大量非警觉节点的接触快速的扩散流行病，其中这些非警觉节点并没有流行病相关的意识，防护能力较为脆弱。所以选取较大的a值时在前期会产生峰值，随着时间的推进，警觉个体逐渐增多，流行病的感染率才会逐渐稳定。

与采取个体行为1的情况类似，当在采取个体行为2时取较大的a值会使得前期已感染流行病的警觉个体和不具备警觉意识的个体接触，其中有着相当比例的易感个体，因此流行病的感染率在前期会出现短暂的峰值，随着时间的增加，网络中个体的流行病感染率会逐渐稳定。

根据模型模拟结果得出应对流行病传播的指导意见。由附图3及图4所示所示，当选择个体警觉性策略1时，应指导民众尽量选择和同样警觉的邻居接触，并且应降低警觉性。当选择个体警觉性策略2时，应指导民众选择和非警觉的邻居接触，并且应提高警觉性。

通过仿真，验证了本发明能够有效降低流行病的感染率，验证了本发明的优越性。本发明的模型不仅能够描述社会接触网络中的流行病传播与信息意识扩散的过程，而且能够考虑到信息意识对于个体行为影响的异质性，可以更好地研究复杂网络中的病毒传播动力学行为，并对现实生活中对流行病的传播的应对具有指导意义。

以上所述仅是本发明的优选实施方式，应当指出：对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。