一种钛铝合金定向凝固过程晶粒生长的三维数值模拟方法

本发明属于金属材料铸造工艺数值模拟技术领域，具体涉及一种钛铝合金定向凝固过程晶粒生长的三维数值模拟方法。

背景技术：

金属凝固过程中组织的演变一直是研究金属材料组织性能中的一大难关。由于金属凝固过程的不确定性与瞬时性使得金属材料组织的实验性研究比较困难。而随着计算机领域与凝固理论基础的不断发展，大量学者将目光聚焦在用数值模拟的方法对金属凝固过程中的组织演变进行数值模拟并取得一定的成果。

发展至今，已经出现并用于模拟金属凝固组织的方法有确定性方法、随机性方法与相场法(pf)，随机性方法又分为蒙特卡罗(mc)法与元胞自动机法(ca法)，而在其中较为著名并应用广泛的是相场法(pf)与元胞自动机法(ca法)。元胞自动机法虽发展时间稍晚，但以其独特的方法迅速发展并在模拟金属微观组织演变上取得了不菲的成果。

从上世纪八十年代开始，相继有学者对用ca法模拟凝固过程中组织的演变进行研究，并在此过程中建立了多种耦合模型，例如ca-fe模型、ca-pe模型等，并且从晶粒形核与生长状态、晶粒大小、晶粒分布特征、晶粒组织转变等方面进行数值模拟，将得到的二维数值模拟图与实验进行对比，验证了数值模拟的可行性与准确性。

金属凝固过程中晶粒组织演变的二维数值模拟模型的建立已颇具成效，但三维数值模拟模型运用尚不广泛，而建立一个用于研究金属凝固过程组织演变的三维模型可以更直观、多维度的观察晶粒组织形态的演变。因此建立一种合金定向凝固过程中晶粒生长的三维数值模拟方法尤为重要。

技术实现要素：

本发明的目的是提供一种钛铝合金定向凝固过程晶粒生长的三维数值模拟方法，打破了现有技术中金属组织凝固多为二维模拟的现状，提供了一种可供研究者更直观、多角度观察晶粒组织生长的方法。

本发明所采用的技术方案是，一种钛铝合金定向凝固过程晶粒生长的三维数值模拟方法，其特征在于，具体按以下步骤实施：

步骤1，简化模型建立条件；

步骤2，建立形核与生长模型；

步骤3，建立溶质再分配与扩散模型；

步骤4，定义捕获规则；

步骤5，模拟计算及结果导出。

本发明的特点还在于：

其中步骤1中简化模型条件具体包括以下内容：

简化条件1：整个凝固过程只存在液相、固相和界面三种元胞状态；

简化条件2：元胞邻域关系采用空间三维元胞邻域关系；

简化条件3：忽略动力学过冷，只考虑温度过冷、成分过冷和曲率过冷；

简化条件4：模拟区域划分为正方体网格，每一个网格即为一个元胞；

其中步骤2中建立形核与生长模型的具体过程为：

将模拟区域整体定义为液相元胞，在凝固起始位置定义若干个固相元胞作为凝固的初始晶核元胞，初始晶核周围的液相元胞定义为界面元胞；

由金属凝固理论可知，液态金属要凝固必须有过冷度的存在，总过冷度可由公式(1)计算：

式中：tl为液相线温度；t为当前元胞温度；ml为溶质的液相线斜率；c0为溶质的初始浓度；为界面处平衡液相分数；γk为gibbs-thompson系数；ε为表面能各向异性强度；θ为界面法向和水平方向的夹角，θ0为晶体的择优生长方向和水平方向的夹角；

界面曲率的计算公式(2)如下：

式中：表示元胞n中固相的份数；

给定过冷度后，界面处平衡液相分数可由公式(3)计算：

界面元胞与液相元胞在δt时间内通过界面面积排出的溶质可由公式(4)进行计算：

式中：dl为液相扩散系数；δx为模拟选用的网格尺寸；δt为单位时间；nb为界面元胞的液相邻胞；cnb为液相邻胞浓度；

此时，界面元胞的固相分数增量可由公式(5)计算：

式中：a为扰动因子；k0为平衡分配系数；rand()能够在[0,1]产生一个随机数；

其中步骤3中建立溶质再分配与扩散模型的具体过程为：

当凝固的下一时间步长内有δfs的液相转变为固相时，则δt时间内排出的溶质可由公式(6)、(7)确定：

式中：为某一时刻界面元胞液相溶质浓度；fs⁰为固相率，界面元胞生长过程中排出的溶质会导致枝晶周围液相溶质浓度升高，液相元胞的溶质扩散可由公式(8)计算：

式中：dl为液相扩散系数，n为界面元胞个数；

其中步骤4中定义捕获规则的具体过程为：

选定初始晶核元胞，对该初始晶核元胞周围的界面元胞进行固相分数求解并判定，若界面元胞的固相分数大于1，则该界面元胞转变为固相元胞，新转变的元胞周围的液相元胞则被捕捉成为新的界面元胞；

对上述所得新转变的固相元胞周围的界面元胞进行固相分数求解并判定，界面元胞的固相分数大于1，则该界面元胞转变为固相元胞，新转变的固相元胞周围的液相元胞则被捕捉成为新的界面元胞，以此类推，直至所有液相元胞转变为固相元胞；

其中步骤5中模拟计算及结果导出具体按以下步骤实施：

步骤5.1，基于步骤1～4所构建的ti-45％al合金定向凝固过程模型进行编程；

步骤5.2，将编好的程序导入模拟软件matlab中，输入ti-45％al合金的热物性参数，即得到ti-45％al合金定向凝固过程的模拟结果。

本发明的有益效果是：

(1)本发明提供一种钛铝合金定向凝固过程晶粒生长的三维数值模拟方法，打破了现有技术中金属组织凝固多为二维模拟的现状，提供了一种可供研究者更直观、多角度观察晶粒组织生长的方法；

(2)本发明可以模拟金属凝固过程中组织演变的动态变化，为进一步研究合金凝固机理提供了一种新的研究方法；

(3)传统的实验方法研究合金的铸造与凝固过程需要经过制模、混砂、造型制芯、熔炼、浇注、凝固、清理以及后续的组织成分、力学性能、机械性能等的检测，可见，传统的实验方法过程繁琐、费时费力，而且在凝固过程中无法做到对合金温度场及组织场演变的实时监测，相对于传统的实验方法，本发明对合金的凝固条件作了一定的简化，通过编程利用计算机模拟软件对合金的凝固过程以及组织演变进行了模拟，节省了大量的人力物力投入，经济高效且节能环保。

附图说明

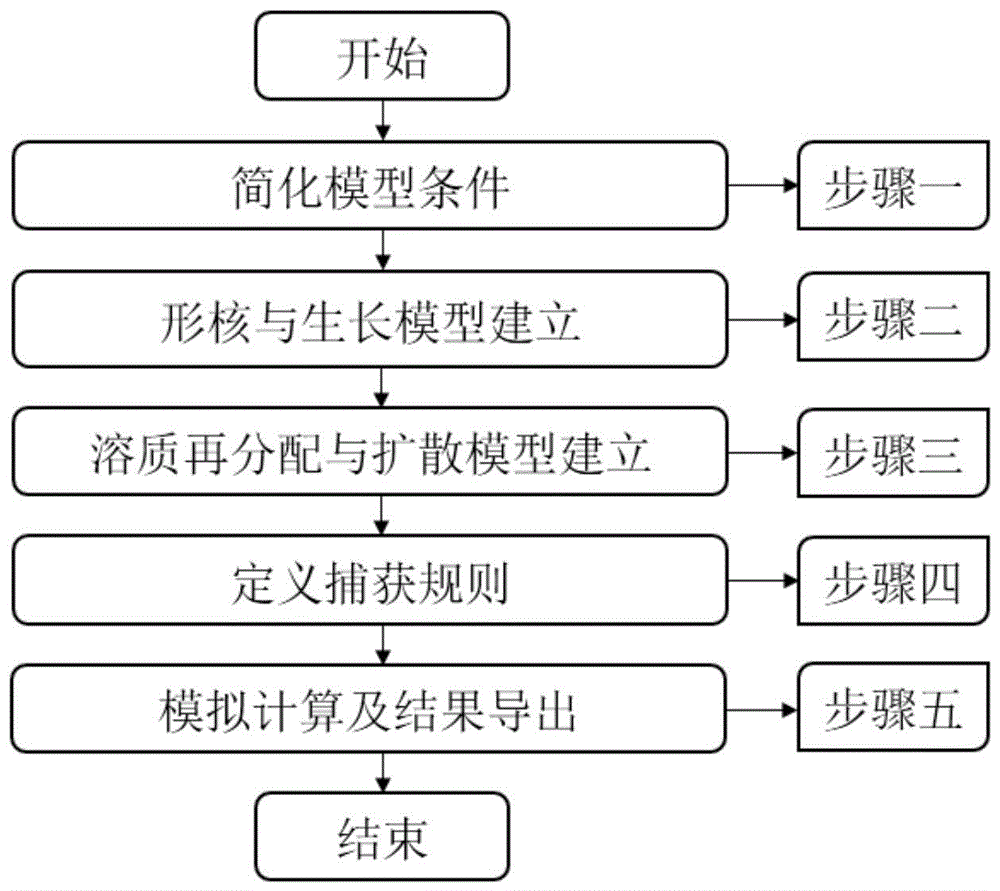
图1是本发明一种钛铝合金定向凝固过程晶粒生长的三维数值模拟方法技术的流程图；

图2是本发明一种金属凝固过程中组织的三维数值模拟演变方法的空间领域元胞关系示意图；

图3是实施例1ti-45％al合金的不同时间下枝晶生长形貌图；

图4是实施例2ti-45％al合金的不同扰动振幅下枝晶生长形貌图；

图5是实施例2ti-45％al合金的不同过冷度下枝晶生长形貌图。

具体实施方式

下面结合附图和具体实施方式对本发明进行详细说明。

本发明提供了一种钛铝合金定向凝固过程晶粒生长的三维数值模拟方法的流程图，如图1所示，具体按照以下步骤实施：

步骤1简化模型建立条件包括：

简化条件1：整个凝固过程只存在液相、固相和界面三种元胞状态；

简化条件2：元胞邻域关系采用空间三维元胞邻域关系；

简化条件3：忽略动力学过冷，只考虑温度过冷、成分过冷和曲率过冷；

简化条件4：模拟区域划分为正方体网格，每一个网格即为一个元胞；

步骤2，建立形核与生长模型按照以下具体步骤实施：

将模拟区域整体定义为液相元胞，在凝固起始位置定义若干个固相元胞作为凝固的初始晶核元胞，初始晶核周围的液相元胞定义为界面元胞；

由金属凝固理论可知，液态金属要凝固必须有过冷度的存在，总过冷度可由公式(1)计算：

式中：tl为液相线温度；t为当前元胞温度；ml为溶质的液相线斜率；c0为溶质的初始浓度；为界面处平衡液相分数；γk为gibbs-thompson系数；ε为表面能各向异性强度；θ为界面法向和水平方向的夹角，θ0为晶体的择优生长方向和水平方向的夹角；

界面曲率的计算公式(2)如下：

式中：表示元胞n中固相的份数；

给定过冷度后，界面处平衡液相分数可由公式(3)计算：

界面元胞与液相元胞在δt时间内通过界面面积排出的溶质可由公式(4)进行计算：

式中：dl为液相扩散系数；δx为模拟选用的网格尺寸；δt为单位时间；nb为界面元胞的液相邻胞；cnb为液相邻胞浓度；

此时，界面元胞的固相分数增量可由公式(5)计算：

式中：a为扰动因子；k0为平衡分配系数；rand()能够在[0,1]产生一个随机数；

步骤3建立溶质再分配与扩散模型具体按照以下步骤实施：

当凝固的下一时间步长内有δfs的液相转变为固相时，则δt时间内排出的溶质可由公式(6)、(7)确定：

式中：为某一时刻界面元胞液相溶质浓度；fs⁰为固相率，界面元胞生长过程中排出的溶质会导致枝晶周围液相溶质浓度升高，液相元胞的溶质扩散可由公式(8)计算：

式中：dl为液相扩散系数，n为界面元胞个数；

步骤4，定义捕获规则具体按照以下步骤实施：

选定初始晶核元胞，对该初始晶核元胞周围的界面元胞进行固相分数求解并判定，若界面元胞的固相分数大于1，则该界面元胞转变为固相元胞，新转变的元胞周围的液相元胞则被捕捉成为新的界面元胞；

对上述所得新转变的固相元胞周围的界面元胞进行固相分数求解并判定，界面元胞的固相分数大于1，则该界面元胞转变为固相元胞，新转变的固相元胞周围的液相元胞则被捕捉成为新的界面元胞，以此类推，直至所有液相元胞转变为固相元胞；

步骤5，模拟计算及结果导出按照以下步骤实施：

步骤5.1，基于步骤1～4所构建的ti-45％al合金定向凝固过程模型进行编程；

步骤5.2，将编好的程序导入模拟软件matlab中，输入ti-45％al合金的热物性参数，即得到ti-45％al合金定向凝固过程的模拟结果。

表1为ti-45％al合金模拟时计算所用热物性参数

下面通过实施例对模拟结果进行分析，其中实施例1中其他参数不变，对不同时间下的枝晶形貌进行了分析；实施例2中其他参数不变，对不同扰动振幅下的枝晶形貌进行了分析；实施例3中其他参数不变，对不同过冷度下的枝晶形貌进行了分析。

实施例1

向本发明编程好的模型中输入表1ti-45％al合金的各项热物性参数，经计算得到ti-45％al合金不同时间下枝晶生长形貌，模拟结果如图3a、3b所示。可以看出，当晶粒在形核点完成形核，由于特定的温度梯度，晶粒主枝晶开始向上生长，同时生成一些二次枝晶，由于不同晶粒间的生长相互影响，不同晶粒的二次枝晶形成相互阻碍的趋势。

实施例2

向本发明编程好的模型中输入表1ti-45％al合金的各项热物性参数，在其他条件不变的情况下，扰动振幅分别为0.2和2时的枝晶生长形貌，模拟结果如图4a、4b所示。通过对比发现，当其他条件不变时随扰动振幅增大，二次枝晶粗化的同时其生长幅值也有所下降，但是二次枝晶的生长间距并没有明显改变。

实施例3

向本发明编程好的模型中输入表1ti-45％al合金的各项热物性参数，在其他条件不变的情况下，过冷度分别为2和10时的枝晶生长形貌模拟，结果如图5a、5b所示。通过对比可以发现，当其他条件不变时，随着过冷度的增加，枝晶生长速度亦随之增加，且一次枝晶生长速度最快，当过冷度增加到一定值时，二次枝晶相继生长，一次枝晶的生长优势慢慢消失直至被二次枝晶的生长所取代。