模拟颤振环境铰链机构运动分子动力学仿真模型及方法

本发明属于分子动力学技术领域，具体涉及一种模拟颤振环境铰链机构运动分子动力学仿真模型及方法。

背景技术：

航天器在轨运行期间反复进出地球阴影，温度交替变化范围宽，且随轨道高度和季节等变化而变化，导致空间机构经受反复剧烈的温度交替，这种长期剧烈的温度交替使得材料内部积攒了大量内力，将导致机械结构的低频振动。且因空间微重力环境的存在，重力与其他作用力相比较小，航天机构易受摩擦力矩而发生抖动，且不会很快恢复至平衡位置，而是在平衡位置附近做无规则抖动，这将引起机构的颤振，导致碰撞摩擦，严重影响精密设备的运动和稳定性。

对于地面环境而言模拟微重力较为困难，成本高，且实验的方式很难观测到动态摩擦过程，数值模拟方法成为解决这一问题的有效途径。分子动力学方法是目前应用广泛的计算复杂体系的方法，发展至今，研究学者建立了许多适用于不同材料体系的力场模型，极大地提升了计算复杂体系结构与热力学性质的能力及准确性，其模拟系统中粒子的运动具有了确定的物理依据。同时可获得系统的动态特性与热力学统计数据，为相关研究的理论分析提供了重要依据。

碰撞滑动摩擦是摩擦学研究的一种，现有基于分子动力学的摩擦学研究，如2018年发表于期刊《amoleculardynamicssimulationstudy》第8卷第3期129页的文章《theinfluenceofverticalvibrationonnanoscalfriction》,通过分子动力学研究了振动对纳观摩擦的影响，指出摩擦力存在一定的频率依赖性，通过给压头施加强迫振动，考虑了压头振动对摩擦的影响，却忽略了基体因压头振动而产生随动的现象。而实际的工况条件下，轴孔会因销轴的振动而产生颤振现象，因此单纯考虑销轴的振动而忽略轴孔的随动无法体现真实的运动过程。本发明通过建立分子动力学仿真模型，给压头施加强迫正弦振动来模拟销轴的振动，同时在基体的y向和z向施加弹簧来模拟轴孔的随动，以此来进行颤振环境下的摩擦学研究仿真分析。

技术实现要素：

要解决的技术问题：

为了避免现有技术的不足之处，本发明提出一种模拟颤振环境铰链机构运动分子动力学仿真模型及其构建方法，通过压头和基体对颤振环境下铰链机构摩擦磨损的微观机理进行模拟，分析振动对其摩擦力的影响。

本发明的技术方案是：一种模拟颤振环境铰链机构运动分子动力学仿真模型，其特征在于：包括压头、基体和弹簧，所述压头为圆柱体结构，用于模拟铰链机构中轴的运动；所述基体为长方体结构，通过弹簧安装于压头的下方，用于模拟铰链机构中轴孔的随动；所述压头的轴向平行于基体顶面；

所述弹簧包括第一弹簧和第二弹簧，所述第一弹簧的轴向沿z向设置，并垂直固定于基体底面中心，模拟铰链中z向运动；所述第二弹簧的轴向沿y向设置，并垂直固定于基体侧壁底边中心，模拟铰链中y向运动。

一种模拟颤振环境铰链机构运动分子动力学仿真模型的构建方法，其特征在于具体步骤如下：

步骤一：依据铰链机构运动特性，在模拟软件中设置系统的边界条件，选取原子相互作用势函数；设定系统的初始条件，即初始位置和初始速度；并选定时间步长，构建分子动力学仿真模型；

步骤二：通过在基体的y向和z向设置弹簧，实现基体随压头振动的随动状态；

步骤三：压头y向和z向施加强迫正弦振动，同时给压头施加水平速度vs，在微正则系综下开始碰撞滑动摩擦；

步骤四：对步骤三在微正则系综下进行的碰撞滑动摩擦过程进行分子动力学仿真计算，统计计算结果，得到不同振动频率下压头与基体的位置坐标以及碰撞滑动过程中压头受到的摩擦力曲线。

本发明的进一步技术方案是：所述步骤一中，构建分子动力学仿真模型的具体步骤如下：

步骤1：根据铰链机构的运动特性，在软件中建立模拟铰链机构的压头与基体模型；所述基体包括固定层、恒温层和牛顿层，将基体底部和x向的相对两侧a范围内的原子设置为固定层原子；将底部固定层上方的a范围内原子设置为恒温层原子，用以吸收摩擦过程中产生的热量；基体内其余原子设置为牛顿层原子；恒温层和牛顿层内的原子遵循牛顿第二运动定律；

步骤2：设定模拟区域x向和y向为周期性边界条件，用以减小尺寸效应；

步骤3：通过系统内不同元素原子之间相互作用势函数，获得原子之间的相互作用；

步骤4：根据maxwell-boltzmann能量分布函数设定系统内所有原子的初始速度，从而建立压头和基体原子分配的初始速度，该速度对应于其各自平衡状态的温度；设定系统温度为300k，积分步长选择为1fs；

步骤5：完成步骤1-4的设定后，在正则系综nvt下，依据所设定系统内各原子的初始位置和初始速度，根据选取的势函数计算系统中各原子的势能、位置及速度，对压头和基体原子进行平衡约束，以使系统初始模型达到平衡状态；系统弛豫完成后，在微正则系综microcanonical.nve下对系统进行内部平衡态演化，使系统达到平衡状态。

本发明的进一步技术方案是：所述步骤1中，利用lammps软件构建基体为非金属硅的晶体模型，硅的晶格结构为金刚石结构，晶格常数a为0.543nm，模型在x，y和z方向上分别对应晶向[100]、[010]和[001]，各向尺寸为50a×16a×25a，包含有162416个硅原子；所述压头为半径是8a的圆柱形，材料为金刚石。

本发明的进一步技术方案是：所述压头去除上半部分原子，计算时仅保留下半部分的圆柱结构，去除后压头内部共含有30679个碳原子。

本发明的进一步技术方案是：所述步骤3中，包括三种相互作用势：si-si原子、c-c原子以及c-si原子。

本发明的进一步技术方案是：所述si-si原子之间的相互作用通过tersoff多体势函数拟合；金刚石压头和硅基体原子之间的相互作用采用morse电势描述。

本发明的进一步技术方案是：所述步骤二中，模拟颤振环境时，压头振动引起基体位置的变化，进而弹簧发生形变，将弹簧因形变产生的力均分施加于基体固定层的每一个原子上，能够模拟铰链机构中轴孔随轴的振动而产生的随动状态；所述第一弹簧和第二弹簧的刚度系数分别为k1、k2。

本发明的进一步技术方案是：所述弹簧因形变产生的力是：

f＝k×(x1-x0)

其中：k为弹簧的刚度系数，x0为基体初始质心位置，x1为运动过程中基体的瞬时质心位置。

本发明的进一步技术方案是：所述步骤三中，模拟铰链机构的运动特性，将轴的无规则碰撞等效为圆柱体压头在y向和z向所施加的强迫振动的耦合，振动在y向和z向的振幅分别为ay、az；频率分别为fy、fz；同时将轴的旋转运动等效为压头沿基体表面的水平滑动；利用lammps软件的fixmove命令给压头在y向和z向施加正弦强迫振动以及水平方向的滑动速度vs，在微正则系综下开始碰撞滑动摩擦过程；依据步骤二中所设定的弹簧刚度k1、k2，根据以下公式计算得到基体y向和z向的固有频率：

其中：k为弹簧的刚度系数，m为基体的质量；

改变压头的振动频率，根据步骤一中所设定的相关参数以及选取的系统内不同元素原子之间相互作用势函数，计算得到不同振动频率下，压头与基体的位置坐标以及在碰撞滑动过程中压头受到的摩擦力，进行颤振环境下的摩擦学研究的仿真分析。

有益效果

本发明的有益效果在于：本发明根据空间环境下铰链机构的运动特性，将轴的无规则碰撞等效为圆柱体压头在y向和z向所施加的强迫振动的耦合，将轴的旋转运动等效为压头沿基体表面的水平滑动，以此来模拟空间微重力环境下，销轴因受摩擦力矩而发生的无规则抖动；同时本发明在基体底部沿y向和z向各配置一根弹簧，压头因振动引起基体位置的变化最终导致弹簧产生形变，将弹簧因形变产生的力均分施加于基体固定层的每一个原子上，以此来模拟轴孔随销轴的振动产生随动这一现实工况。

与传统研究振动的分子动力学模型相比，本发明模型更加贴近实际的工况条件，提高了模拟结果的准确性。本发明对比了fz＝52.6ghz时基体有无弹簧状态下碰撞滑动过程中基体与压头坐标差曲线以及压头受到的摩擦力大小(如图5所示)。由曲线图5(a)可知基体无弹簧状态下压头与基体之间的坐标差曲线与压头施加强迫振动曲线基本吻合；然而基体有弹簧状态下可以看出因基体存在一定的随动导致了较为剧烈的相对振动。同时从图5(b)可以看出基体有无弹簧状态下的摩擦力也有较大不同，求得有弹簧状态下平均摩擦力为29.66nn，无弹簧状态下平均摩擦力则为59.38nn，因此可见基体随压头振动的随动过程不容忽视。

附图说明

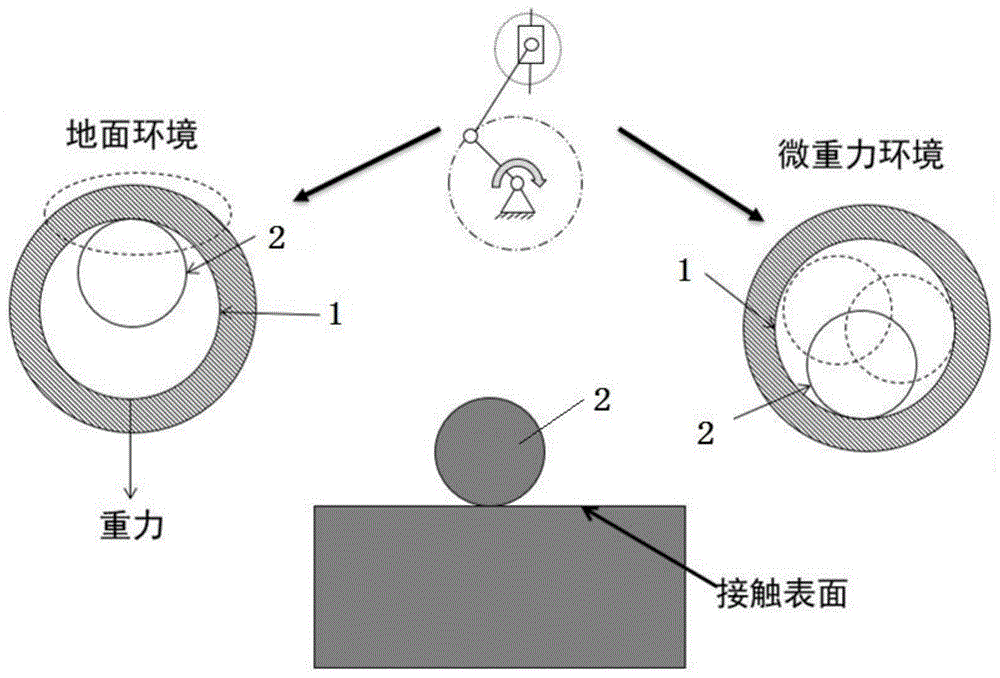
图1为简化铰链机构说明图；

图2为本发明提出的模拟铰链结构的仿真模型；

图3为本发明提出的模拟颤振环境下铰链机构的运动过程仿真模型示意图。

图4为本发明模拟颤振环境铰链机构运动的流程图；

图5为fz＝52.6ghz下基体有无弹簧结果对比曲线图；

图6为本发明实施例中fz＝36.6ghz以及fz＝52.6ghz下坐标差与摩擦力结果对比曲线图；

图7为本发明模拟过程中基体瞬态缺陷结构横截面图。

附图标记说明：1.孔，2.轴，3.压头，4.基体。

具体实施方式

下面通过参考附图描述的实施例是示例性的，旨在用于解释本发明，而不能理解为对本发明的限制。

本实施例提供了一种模拟颤振环境铰链机构运动分子动力学仿真模型构建方法，包括以下步骤：

步骤一、依据铰链机构运动特性，设置系统的边界条件，选取原子相互作用势函数，设定系统的初始条件以及相关模拟参数，构建分子动力学仿真模型；

该步骤包括以下子步骤：

子步骤1，依据铰链机构运动特性，简化铰链机构模型；根据铰链机构的运动特性，简化铰链机构为圆柱形压头与长方体形基体，如图2所示。利用lammps软件构建非金属硅(si)的晶体模型，硅的晶格结构为金刚石结构，晶格常数a为0.543nm，模型在x，y和z方向上分别对应晶向[100]、[010]和[001]，各向尺寸为50a×16a×25a，包含有162416个硅原子。随后构建半径为8a的圆柱形压头，材料为金刚石，为了节约计算时长，去除压头上半部分原子，压头内部共含有30679个碳原子。此外为了防止基体偏移，将基体最底部和两侧a范围内原子设置为固定层原子(fixed)；将底部固定层上方的a范围内原子设置为恒温层原子以吸收摩擦过程中产生的热量；其余原子为牛顿层原子；恒温层和牛顿层内的原子遵循牛顿第二运动定律。

子步骤2，设置系统的边界条件；由于计算机性能、算法效率及精度的限制，为了减少模拟系统的规模远小于实际规模带来的尺寸效应，只能选取一定体积的材料作为原胞，根据边界条件来执行分子动力学计算，本实施例在x和y方向采取了周期性边界条件；

子步骤3，选取原子相互作用势函数；分子动力学模拟计算中，选择合适的势函数是获得准确结果的必要条件，分子动力学发展至今已建立了许多适用于不同材料体系的力场模型，查阅相关文献，选择不同元素之间的势函数来描述原子之间的相互作用。本实施例中存在三种不同的相互作用势：si-si原子(硅基体内部原子势函数)、c-c原子(压头的内部原子势函数)以及c-si原子(压头与基体之间的势函数)。相对于si而言，金刚石的硬度则大的多，因此可将金刚石压头视为刚体，从而忽略c-c原子之间的相互作用；参考相关文献，对于具有金刚石立方结构的共价体系，应考虑其共价键和键角的影响，这正是tersoff多体势函数所擅长的，本实施例模拟过程选用tersoff多体势函数来拟合si-si原子之间的相互作用；选用morse电势来描述金刚石压头和硅基体原子之间的相互作用。

子步骤4，设定系统的初始条件以及相关模拟参数；初始条件是指开始进行模拟时系统各个原子的速度和位置，分子动力学计算本质为根据初始值对方程进行积分求解的过程。系统中原子的初始速度产生的原理为：根据由指定温度产生的随机数生成速度集合，将此随机数乘以原子的平均速率即可得到符合maxwell-boltzmann的原子速度。根据maxwell-boltzmann能量分布函数为建立的压头和基体原子分配初始速度，该速度对应于它们平衡状态的温度；设定系统温度为300k，积分步长选择为1fs。由于在本实施例中所设定的压头材质为刚性，因此对其不予设定初始速度；如将压头的材质设定为非刚性，则需要对其设定初始速度。

完成以上条件的设定后，在正则系综(nvt)下，依据所设定系统内各粒子的初始位置和初始速度，根据选取的势函数计算系统中各原子的势能、位置及速度，对压头和基体原子进行平衡约束，以使系统初始模型达到平衡状态。系统弛豫完成后，在微正则系综(microcanonical,nve)下对系统进行内部平衡态演化，使系统达到平衡状态，为后续碰撞滑动摩擦过程的模拟做好准备。

步骤二、基体y向和z向各配置一根弹簧来实现基体随压头振动的随动状态；

颤振环境下，因销轴的不断振动导致轴孔也处于颤振状态，在基体底部沿y向和z向各配置一根弹簧(如图3所示)，压头振动引起基体位置的变化最终导致弹簧产生形变，弹簧因形变产生的力：

f＝k×(x1-x0)

其中：k为弹簧的刚度系数，x0为计算得到的基体初始质心位置，x1为运动过程中基体的瞬时质心位置。将此力均分施加于固定层(fixed)的每一个原子上，带动基体运动，以此来模拟孔随轴的振动而产生的随动状态。弹簧的刚度系数分别为k1、k2，其大小取决于与铰链结构相连接的构件的刚度，本实施例给定k1＝600n/m，k2＝400n/m。通过该步骤的设定，使基体能够因压头的振动而产生相应的随动，更加贴近真实工况。

步骤三、压头y向和z向施加强迫正弦振动，同时给压头施加水平速度vs；

如图1所示，根据空间环境下铰链机构的运动特性，将轴的无规则碰撞等效为圆柱体压头在y向和z向所施加的强迫振动的耦合，振动在y向和z向的振幅分别为ay、az；频率分别为fy、fz；同时将轴的旋转运动等效为压头沿基体表面的水平匀速滑动；利用lammps软件的fixmove命令给压头施加水平方向的滑动速度vs的同时，在压头y向和z向施加正弦强迫振动(如图3所示)，本实施例给定压头的水平滑动速度为vs＝50m/s，在y向和z向所施加的强迫振动的振幅为ay＝az＝0.55nm，依据步骤b中所设定的弹簧刚度k1、k2，根据公式：

其中：k为弹簧的刚度系数，m为基体的质量。可计算出基体y向和z向的固有频率，调整不同的压头振动频率来研究振动频率对摩擦力的影响。依据本实施例给定k1＝600n/m，k2＝400n/m，根据公式计算得到基体y向和z向的固有频率分别为44.9ghz和36.6ghz。本实施例参照单一变量原则，在fy＝50ghz的条件下，选取fz＝36.6ghz以及fz＝52.6ghz，研究不同z向振动频率对碰撞滑动过程中摩擦力的影响。

d、数据处理与可视化处理

通过lammps软件对自行编写的程序文件进行分子动力学仿真计算。依据步骤a所设定的系统边界条件，原子相互作用势函数等，依据verlet积分算法，在微正则系综下进行碰撞滑动过程分子动力学仿真计算，统计计算结果，得到不同振动频率下压头与基体的位置坐标以及碰撞滑动过程中压头受到的摩擦力曲线(如图6所示)，可以看到fz＝36.6ghz时，因压头z向振动频率等于基体z向固有频率，因此发生共振现象，压头与基体之间坐标差曲线最终收敛；而fz＝52.6ghz时，可以看到发生了较为剧烈的振动；由图6(b)可以分析得到颤振环境下平均摩擦力具有一定的频率依赖性；同时使用ovito软件对分子动力学模拟的数据进行可视化分析，可直观地看到碰撞滑动过程中发生的原子瞬态结构缺陷(图7所示)。

尽管上面已经示出和描述了本发明的实施例，可以理解的是，上述实施例是示例性的，不能理解为对本发明的限制，本领域的普通技术人员在不脱离本发明的原理和宗旨的情况下在本发明的范围内可以对上述实施例进行变化、修改、替换和变型。