基于梯度提升决策树的ERα拮抗剂的生物活性定量预测方法

基于梯度提升决策树的er
α
拮抗剂的生物活性定量预测方法
技术领域
1.本发明涉及生物制药和机器学习技术领域，尤其涉及基于梯度提升决策树的erα拮抗剂的生物活性定量预测方法。


背景技术：

2.乳腺癌是发生于乳腺上皮或导管上皮的一种恶性肿瘤，发病机制不明，且具有一定的遗传性。它是一类比较常见且具有较高死亡率的癌症。根据数据统计，乳腺癌常发病于女性之间，而男性患者较为罕见，令人担忧的是，近年来，乳腺癌的发病人口持续增加，且患者愈加年轻化。目前常见的乳腺癌治疗方法包含以下五种：1)手术治疗；2)化疗；3)放射治疗；4)靶向治疗；5)激素治疗。
3.大量的数据显示，超过一半的乳腺癌患者的雌激素受体α亚型异常，因而雌激素受体α亚型(erα)在乳腺癌的临床治疗中具有重要意义。选取合适的候选药物拮抗erα活性是治疗乳腺癌的一种重要的临床手段。目前，在拮抗erα活性的药物临床研发过程中，为了降低研发成本，提高效率，针对雌激素受体α亚型，在数据库中抓取大量应用于该目标的化合物以及其相关数据，然后基于化合物的分子结构描述和其生物活性值，建立化合物的
‘
结构-活性’的定量预测方法。
4.传统的机器学习算法主要包括：线性回归、梯度提升决策树、随机森林、支持向量机等。梯度提升决策树作为机器学习重要算法之一，是一种迭代决策树算法，该算法由多棵决策树组成，将所有决策树的结论进行累加即为模型最终输出的结果，是一种泛化能力较强的算法。
5.由于无法确定生物活性值与选取的自变量之间的关系，需要构建多元回归模型，具体可分为多元线性回归/非线性回归模型。然而线性和非线性的多元回归模型并不能很好的进行拟合。因此，我们选用了机器学习模型下的梯度决策树作为回归模型，并划分数据集进行训练。
6.如何解决上述技术问题为本发明面临的课题。


技术实现要素：

7.为了解决以上技术问题，本发明提供了基于梯度提升决策树的erα拮抗剂的生物活性定量预测方法，并通过训练的梯度提升决策树模型实现回归估计。
8.本发明是通过以下措施实现的，包含以下步骤：
9.1、对影响erα拮抗剂的生物活性的变量数据进行预处理：
10.(1)统计各个自变量的所有样本数据全为零的情况，将列中样本数据全为零的变量进行删除。
11.2、变量的筛选
12.(1)皮尔逊(pearson)相关系数筛选线性相关变量
13.皮尔逊相关系数是一种用以描述两个变量之间线性相关性的度量方法，它在区
间-1到 1之间取值。
14.皮尔逊相关系数的定义为：
[0015][0016]
取两个随机变量x,y的n个观测值，其中xi,yi分别代表变量x,y的第i个观测值，分别代表两个变量的均值。
[0017]
表1皮尔逊相关系数度量值
[0018]
|r|取值|r|＝0时|r|≤0.5时0.5≤|r|《1时|r|＝1时关联程度不相关弱相关强相关完全相关
[0019]
(2)互信息筛选非线性相关变量
[0020]
上世纪末，batttiti首次基于互信息原理进行特征筛选。通俗地讲，互信息下的特征选择就是从高维的原始特征中，选取与目标变量高度相关的特征。理论上的操作就是对因变量与自变量求取互信息，选取互信息值比较大的自变量作为目标特征。
[0021]
信息熵：
[0022]
选取一个随机变量x，xi,i＝{1,2,3
…
,n},是变量x的一组观测值，p(x)为变量x取值x 时的概率，信息熵如下表示:
[0023][0024]
当h(x)取值越大时，变量x越不确定。
[0025]
条件熵：
[0026]
在选定随机变量x的条件下，定义随机变量y关于x的条件熵：
[0027][0028]
其中p(x,y)为随机变量x与y的联合概率密度，p(y/x)为在确定x的条件下变量y的条件概率密度。
[0029]
互信息：
[0030]
i(x；y)＝h(x)-h(x/y)
[0031]
在上述基础上，利用算法，依次计算因变量(生物活性)与自变量(分子描述符)的互信息，互信息值越大，两者之间的相关性越强，即该分子描述符对生物活性具有很强作用，然后根据互信息大小进行排序，选取前200个与生物活性相关性强的作为目标特征变量。
[0032]
(3)随机森林筛选
[0033]
随机森林的基本分类器是决策树，它是一种较为普通的机器算法，结构类似于倒立的树，由根节点，内部节点以及叶子节点组成，每一个非叶子节点都表示一个决策。
[0034]
特征重要性度量：
[0035]
假设有n个样本数据，m个特征集，从样本数据中有放回地随机抽取n(n《n)个样本作为训练集，剩下的样本数据作为测试集(袋外样本)，从特征集中有放回地随机抽取 m(m《m)个特征。重复操作k次，选出k棵树组成一个随机森林。选定一棵树，它包含m 个特征，对于这棵树中的某个特征，在测试集中，随机改变关于这个特征样本数据，求解前后的测试集误差率的差值作为该特征在这棵树中的重要程度。基于此，可以计算出所有特征在各棵树中的重要程度。然而，这只是得出了某个特征在某些树中的重要程度，而不能作为该特征在整个森林中的重要程度。从上述分析中可以看出，每个特征在多棵树中重复出现，因而求取这个特征值在多棵树中的重要程度的平均值作为该特征在森林中的重要程度。
[0036]
特征重要性度量公式：
[0037][0038]
其中nt表示特征mi在森林中出现的次数。errorb
t2
表示第t1棵树中特征值改变之后的袋外误差，errorb
t1
表示第t1棵树中正常值的袋外误差。
[0039]
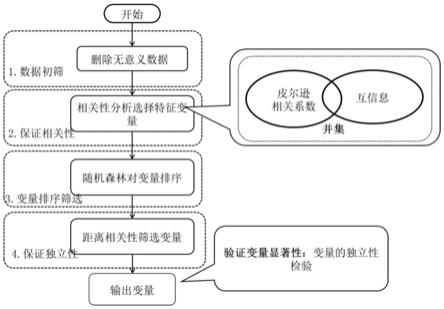
特征变量选择：
[0040]
特征权值反映了操作变量的重要程度占比，对每一个操作变量的特征权值，计算其特征权值，具体公式为：
[0041][0042]
其中，weight(mi)为特征mi的特征权值，mdm(mi)为特征mi的平均袋外数据误差，m 为特征总数；
[0043]
3、独立性检验
[0044]
(1)距离相关系数
[0045]
目前已有很多成熟的算法衡量变量之间的相关性，例如皮尔逊相关系数，然而皮尔逊相关系数只对具有线性关系的变量有意义，对于非线性关系的变量，即使系数为0，也不能说明两个变量之间相互独立。距离相关系数的提出弥补了这部分的不足，它的优势在于，无论两个变量之间是线性还是非线性的，都可以应用距离相关系数算法求解两个变量之间的相关性，其次它不受任何条件约束，这大大扩大了该算法的应用范围，更具一般性。
[0046]
用dcorr(x,y)衡量变量x和y之间的独立性，当dcorr(x,y)为0时，变量x和y彼此独立；当dcorr(x,y)值越大，两个变量之间的相关性越强，变量x和y之间的相关性与系数值呈正比。设(xi,yi)，其中i＝{1,2,3,
…
,n}是总体(x,y)之间的观测值，||x
i-xj||2为xi与xj之间的二范数。
[0047][0048]
其中
[0049]
[0050][0051][0052]
同理可得
[0053][0054][0055]
为了获得彼此相对独立的自变量，要求自变量之间关系为不相关或弱相关。
[0056]
4、模型建立：
[0057]
梯度提升决策树(gbdt gradient boosting decision tree)是一种迭代的决策树算法，该算法由多棵决策树组成，将所有决策树的结论进行累加即为模型最终输出的结果，是一种泛化能力较强的算法。该模型中的子树为回归树，即回归树的每个节点都会输出一个预测值，该预测值一般为该节点中所有样本的均值。因此梯度提升决策树常用于用来做回归预测任务中。
[0058]
梯度提升决策树的算法步骤如下所示：
[0059]
1)初始化，估计使损失函数极小化的常数值，它是只有一个根节点的树，即ganma是一个常数值。
[0060]
2)流程操作
[0061]
(1)计算损失函数的负梯度在当前模型的值，将它作为残差的估计
[0062]
(2)估计回归树叶节点区域，以拟合残差的近似值
[0063]
(3)利用线性搜索估计叶节点区域的值，使损失函数极小化
[0064]
(4)更新回归树
[0065]
3)得到输出的最终模型f(x)。
[0066]
与现有技术相比，本发明的有益效果在于：
[0067]
(1)本发明在数据的采集过程中，因为采集方式、生产环境等因素的影响，采集的数据可能会存在一些问题，因此先对数据进行预处理，删除全为零的列，降低了不良数据对预测模型的影响，也加快了变量的筛选速度。
[0068]
(2)本发明通过传统方法和机器学习方法筛选出特征变量，再通过特征变量建立erα拮抗剂的生物活性定量预测模型。
[0069]
(3)本发明选取1974个化合物对erα的生物活性数据，每个样本数据中包含729个分子描述符信息(即自变量)，每一个样本都有不同的操作和一个对应的生物活性值(用ic
50
表示，为实验测定值，单位是nm，值越小代表生物活性越大，对抑制erα活性越有效)对变量进行基于相关系数，基于互信息和基于随机森林方法的处理，分析变量对生物活性值的影响，最后通过距离性系数对筛选出的变量进行验证，通过筛选后的变量对梯度提升决策树
回归模型进行构建，提高了预测结果的准确率，得到化合物的生物活性预测值。同时，相比于线性回归模型和非线性回归模型等方法，这种由数学模型建立对关系既客观又可靠，又节约成本；相较于同样由数学模型建立关系的方法，该方法筛选前20个对生物活性值有显著影响的分子描述符(即自变量)，不仅能够简化模型，还改善模型的通用性，为工程应用提供方便。
附图说明
[0070]
附图用来提供对本发明的进一步理解，并且构成说明书的一部分，与本发明的实施例一起用于解释本发明，并不构成对本发明的限制。
[0071]
图1为本发明中变量筛选流程图。
[0072]
图2为本发明中随机森林下自变量重要性排序图。
[0073]
图3为本发明中自变量去相关图。
[0074]
图4为本发明中26个变量内部相关度分布图。
[0075]
图5为本发明中目标变量相关系数热力图。
[0076]
图6为本发明中定量预测模型建立图。
[0077]
图7为本发明中梯度提升决策树算法图。
具体实施方式
[0078]
下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域技术人员在没有作出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0079]
如图1所示，本发明构建的是化合物对erα拮抗剂生物活性定量预测模型，数据集来自于针对乳腺癌治疗靶标erα，提供的1974个化合物对erα拮抗剂的生物活性数据和1974 个化合物的729个分子描述符信息(即自变量)。
[0080]
本实施例提供了基于梯度提升决策树的erα生物活性定量预测方法，具体步骤如下：
[0081]
步骤1：对影响erα拮抗剂的生物活性的变量数据进行预处理
[0082]
步骤1.1：选取1974个样本数据，统计出729个分子描述符(即自变量)中全列为零的变量，删去数据全为零的变量，可以明显看出全为零的变量对于生物活性值无效，也就是说，这些分子描述符在化合物中的含量对生物活性没有影响力，故剔除这些冗余变量225 个，降低后续工作量，提高工作效率。
[0083]
步骤2：变量的筛选
[0084]
步骤2.1：在步骤1.1中去除225个无效自变量，然后利用皮尔逊相关系数，将剩余的自变量依次与生物活性求取皮尔逊相关性系数，最后根据相关性强弱筛选出前200个与生物活性强相关的分子描述符变量。
[0085]
步骤2.2：在步骤1.1基础上，利用互信息算法，依次计算因变量(生物活性)与自变量(分子描述符)的互信息，互信息值越大，两者之间的相关性越强，即该分子描述符对生物活性具有很强作用，然后根据互信息大小进行排序，选取前200个与生物活性相关性强的作
为目标特征变量，两种特征分析方法各选取的200个自变量，皮尔逊相关系数主要通过分析线性相关关系从而确定自变量，互信息分析方法通过分析非线性相关关系确定自变量，因此，考虑将两种方法选取的结果取并集，同时兼顾了化合物的生物活性与自变量之间的线性-非线性关系，筛选结果如表1所示。
[0086]
表1为化合物的生物活性与自变量之间的线性-非线性关系，筛选结果：
[0087][0088]
步骤2.3：通过随机森林进行特征提取，对特征进行重要性度量，流程为：
[0089]
(1)对每一颗决策树，选择相应的袋外数据，计算所有特征的袋外数据误差，记为 erroob1。
[0090]
(2)在袋外数据集中，随机改变样本在特征处的值，再次计算袋外数据误差，记为 erroob2。
[0091]
(3)假设森林中有n棵树包含某个特征m，则特征m的重要性等于n棵树中特征m的所有袋外数据误差的差值之和的均值。通过特征重要性计算出特征权值，将255个特征变量的特征权值按照特征变量的重要程度的强弱，也就是说依据特征权值的大小降序排列，保留权值大于0.006的特征变量，其重要性排序如图3所示。
[0092]
步骤3：独立性检验
[0093]
步骤3.1：由于上述步骤筛选出的变量之间可能存在高度相关性，从而会对因变量-生物活性产生重复的作用，为了消除这部分影响，利用合适的算法保留彼此独立且对因变量具有高度贡献的特征变量。通过距离相关性系数，设定距离相关系数0.6为阈值，筛选出彼此独立的20个特征变量。去相关流程如图4，距离相关系数热力图如图5所示，筛选后的20个变量相关性热力图如图6所示。
[0094]
步骤4：梯度提升决策树模型建立：
[0095]
步骤4.1：在给定的数据集，利用knn(k最近邻算法)，找出与待处理的50个化合物的数据相似的数据作为新的数据集，应用于后续工作中。其中knn算法的计算方法为欧氏距离/曼哈顿距离，公式如下：
[0096]
欧氏距离：
[0097][0098]
曼哈顿距离：
[0099][0100]
将经由knn(k最近邻算法)处理后得到的新的数据集，按8:2比例随机划分为训练集和验证集，用训练集构建化合物erα生物活性的定量预测模型，然后利用验证集检验预测模型的性能。梯度提升决策树(gbdt gradient boosting decision tree)是一种迭代的决策树算法，该算法由多棵决策树组成，将所有决策树的结论进行累加即为模型最终输出的结果，是一种泛化能力较强的算法。该模型中的子树为回归树，即回归树的每个节点都会输出一个预测值，该预测值一般为该节点中所有样本的均值。因此梯度提升决策树常用于用来做回归预测任务中，梯度提升决策树的算法步骤如图7所示。
[0101]
为了评估所用模型的预测能力，采用决定系数r2作为误差度量指标来衡量模型预测值与实际值之间的关系。决定系数r2的数值越接近1，则说明估计模型的可靠性越高。
[0102]
y的离差平方和sst表示为回归平方和ssr与剩余平方和sse之和。因此决定系数r2为：
[0103][0104]
上式中n-p-1,n-1是sse和sst的自由度。
[0105]
我们分别采用多元线性回归、多元非线性回归和梯度提升决策树来建立生物活性定量预测模型，结果如表2所示：
[0106]
表2三个多元回归预测模型的r2值
[0107][0108]
根据决定系数r2对20个自变量建立的多项式回归模型进行拟合优度检验，得到的结果如下图所示，其中决定系数r2为0.731是最大值；故梯度提升决策树模型相较于上述两种方法构建的模型由明显的优势，因而使用梯度提升决策树模型作为预测模型。
[0109]
步骤4.2：梯度提升决策树模型验证
[0110]
为了验证梯度提升决策树对解决本题预测任务的优秀表现，尝试将智能算法中常见的回归算法设置为对照组，与梯度提升决策树算法做比较，对照组模型的验证方法和上述验证方法相同。本题选用了机器学习算法中常用于回归任务中的决策树回归模型，支持向量机模型，knn(k最近邻)回归模型以及adaboost回归模型。本次验证实验使用相同的训练集与验证集对各个模型进行训练与评估，实验结果如表3：
[0111]
表3四个多元回归预测模型的r2值
[0112][0113]
实验结果表明，梯度提升决策树模型的表现均好于机器学习算法中常见的回归模型，因此选用梯度提升决策树模型预测化合物的生物活性值。
[0114]
以上所述仅为本技术的优选实施例而已，并不用于限制本技术，对于本领域的技术人员来说，本技术可以有各种更改和变化。凡在本技术的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本技术的保护范围之内。