一种微生物培养基优化方法及系统

1.本发明涉及多元统计技术领域，特别是涉及一种微生物培养基优化方法及系统。


背景技术：

2.在现代发酵工业中，培养基优化一直是最重要的研究课题之一，培养基优化不仅可以有效降低发酵成本，还可以提高原材料的利用率与发酵产物的产量与品质，并能降低发酵工程下游处理的难度等。培养基优化主要通过一些试验设计方法来完成，均匀设计就是其中的杰出代表，因为该试验设计只考虑试验范围内试验点的“均匀散布”而不考虑其“整齐可比性”，因此对同一问题进行优化分析，所需的试验次数，明显少于正交试验与中心组合设计等试验设计，所以均匀设计用于培养基优化研究，可以极大地节约优化成本和压缩优化时间。然而研究表明，由于实验次数偏少，均匀设计存在典型的“小样本问题”和“多重共线性”问题，基于最小二乘法建立的回归模型，存在准确性差和可靠性低等问题。
3.目前，“小样本”培养基优化的多元回归建模方法主要有偏最小二乘回归(partial least squares regression，plsr)和支持向量机等。与此同时，解决多元回归共线性问题的方法主要有plsr、岭回归和lasso回归等。因此，plsr能同时解决均匀设计多元回归建模面临的“小样本”和“多重共线性”问题。此外，研究发现plsr处理多重共线性问题的效果优于岭回归，主要体现在回归模型有更小的平均绝对百分误差和更大的复测定系数。并且plsr具有卓越的预测变量的筛选能力，效果明显优于岭回归和lasso回归。
4.然而传统plsr模型常倾向于保留全部建模自变量，即全回归模型(例如最常用的二次多项式plsr模型就包括一次项、平方项和交叉项等所有建模自变量)，因此常导致plsr模型显得异常“庞大和臃肿”，而简洁性和可解释性很差，这是目前亟待解决的关键问题之一。目前常采用变量投影重要性技术(variable importance inprojection，vip)以删除冗余自变量而保留关键自变量的策略去解决该问题。但文献调研发现，这些plsr-vip方法或者没有使用假设性检验就直接删除vip值偏小的非关键自变量，或者仅仅使用全模型筛选出来的关键自变量就直接组成plsr回归模型，而忽略了非关键因素包含的信息，因此这些传统方法不够科学合理，还常导致模型稳健性差，拟合优度和泛化能力下降。


技术实现要素：

5.本发明的目的是提供一种微生物培养基优化方法及系统，可以解决常规plsr回归方程异常“庞大和臃肿”以及简洁性、可解释性和预测泛化能力差的问题。
6.为实现上述目的，本发明提供了如下方案：
7.一种微生物培养基优化方法，包括：
8.以培养基成分为自变量，以实验产物为响应变量进行均匀设计实验得到多个实验样本；
9.根据所述均匀设计实验采用偏最小二乘回归法构建各所述响应变量的plsr全模型，并将所述plsr全模型作为当前模型；所述plsr全模型为表示所述响应变量与所有所述
自变量之间关系的二次多项式形式的数学表达式；
10.判断所述当前模型中是否所有自变量的vip得分均大于第一设定阈值，得到第一判断结果；
11.若所述第一判断结果为是，则将所述当前模型作为最终plsr模型，所述最终的plsr模型用于构建最优微生物培养基；
12.若所述第一判断结果为否，则以当前模型对应的显著性预测变量作为自变量构建各所述响应变量的vip-plsr模型，并将所述vip-plsr模型作为当前模型；所述显著性预测变量为vip得分大于第一设定阈值的自变量；
13.对各所述plsr全模型的决定系数和各所述vip-plsr模型的决定系数进行偏f检验，并判断是否存在统计学显著性差异，得到第二判断结果；
14.若所述第二判断结果为是，则将各所述当前模型作为最终的plsr模型；
15.若所述第二判断结果为否，则返回所述“判断所述当前模型中是否所有自变量的vip得分均大于第一设定阈值”的步骤。
16.可选的，在所述根据所述均匀设计实验采用偏最小二乘回归法构建各所述响应变量的plsr全模型，并将所述plsr全模型作为当前模型之后还包括：
17.计算各所述plsr全模型的决定系数；
18.采用变量投影重要性技术对所述plsr全模型进行处理得到各自变量的vip得分。
19.可选的，在所述对各所述plsr全模型的决定系数和各所述vip-plsr模型的决定系数进行偏f检验，并判断各所述vip-plsr模型是否存在统计学显著性差异，得到第二判断结果之前还包括：
20.计算各所述vip-plsr模型的决定系数；
21.采用变量投影重要性技术对所述vip-plsr模型进行处理得到各显著性预测变量的vip得分。
22.可选的，所述对各所述plsr全模型的决定系数和各所述vip-plsr模型的决定系数进行偏f检验具体为：
23.根据公式计算偏f检验值，其中，f
01
表示偏f检验值，表示plsr全模型的决定系数，表示第i轮vip-plsr模型的决定系数，n表示实验样本的数目，p表示vip-plsr模型中的自变量数目。
24.一种微生物培养基优化系统，包括：
25.实验模块，用于以培养基成分为自变量，以实验产物为响应变量进行均匀设计实验得到多个实验样本；
26.plsr全模型构建模块，用于根据所述均匀设计实验采用偏最小二乘回归法构建各所述响应变量的plsr全模型，并将所述plsr全模型作为当前模型；所述plsr全模型为表示所述响应变量与所有所述自变量之间关系的二次多项式形式的数学表达式；
27.第一判断模块，用于判断所述当前模型中是否所有自变量的vip得分均大于第一设定阈值，得到第一判断结果；
28.第一最终模型确定模块，用于若所述第一判断结果为是，则将所述当前模型作为最终plsr模型，所述最终的plsr模型用于构建最优微生物培养基；
29.vip-plsr模型构建模块，用于若所述第一判断结果为否，则以当前模型对应的显著性预测变量作为自变量构建各所述响应变量的vip-plsr模型，并将所述vip-plsr模型作为当前模型；所述显著性预测变量为vip得分大于第一设定阈值的自变量；
30.偏f检验模块，用于对各所述plsr全模型的决定系数和各所述vip-plsr模型的决定系数进行偏f检验，并判断是否存在统计学显著性差异，得到第二判断结果；
31.第二最终模型确定模块，用于若所述第二判断结果为是，则将各所述当前模型作为最终的plsr模型；
32.循环模块，用于若所述第二判断结果为否，则返回所述“判断所述当前模型中是否所有自变量的vip得分均大于第一设定阈值”的步骤。
33.可选的，所述微生物培养基优化系统，还包括：
34.plsr全模型决定系数计算模块，用于计算各所述plsr全模型的决定系数；
35.plsr全模型自变量vip得分确定模块，用于采用变量投影重要性技术对所述plsr全模型进行处理得到各自变量的vip得分。
36.可选的，所述微生物培养基优化系统，还包括：
37.vip-plsr模型决定系数确定模块，用于计算各所述vip-plsr模型的决定系数；
38.vip-plsr模型自变量vip得分确定模块，用于采用变量投影重要性技术对所述vip-plsr模型进行处理得到各显著性预测变量的vip得分。
39.可选的，所述偏f检验模块具体为：
40.根据公式计算偏f检验值，其中，f
01
表示偏f检验值，表示plsr全模型的决定系数，表示第i轮vip-plsr模型的决定系数，n表示实验样本的数目，p表示模型中的自变量数目。
41.根据本发明提供的具体实施例，本发明公开了以下技术效果：本发明以培养基成分为自变量，以实验产物为响应变量进行均匀设计实验得到多个实验样本；根据均匀设计实验采用偏最小二乘回归法构建各响应变量的plsr全模型，并将plsr全模型作为当前模型；判断当前模型中是否所有自变量的vip得分均大于第一设定阈值，得到第一判断结果；若第一判断结果为是，则将当前模型作为最终plsr模型，最终的plsr模型用于构建最优微生物培养基；若第一判断结果为否，则以当前模型对应的显著性预测变量作为自变量构建各响应变量的vip-plsr模型，并将vip-plsr模型作为当前模型；显著性预测变量为vip得分大于第一设定阈值的自变量；对各plsr全模型的决定系数和各vip-plsr模型的决定系数进行偏f检验，并判断是否存在统计学显著性差异，得到第二判断结果；若第二判断结果为是，则将各当前模型作为最终的plsr模型；若第二判断结果为否，则返回“判断当前模型中是否所有自变量的vip得分均大于第一设定阈值”的步骤，通过循环vip-plsr建模和偏f检验过程解决常规plsr回归方程异常“庞大和臃肿”以及简洁性、可解释性和预测泛化能力差的问题。
附图说明
42.为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动性的前提下，还可以根据这些附图获得其他的附图。
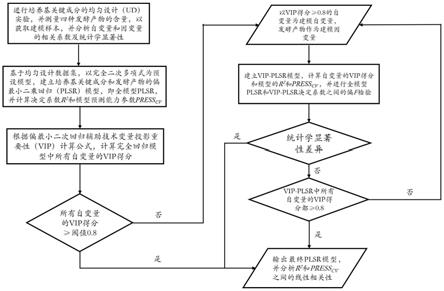
43.图1为本发明实施例提供的一种微生物培养基优化方法的算法流程图；
44.图2为本发明实施例提供的plsr全模型和vip-plsr模型对响应变量的预测值的结果图；
45.图3为本发明实施例提供的vip-plsr建模过程中的vip得分图；
46.图4为本发明实施例提供的vip-plsr建模过程中press
cv
与r2拟合的结果图。
具体实施方式
47.下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
48.为使本发明的上述目的、特征和优点能够更加明显易懂，下面结合附图和具体实施方式对本发明作进一步详细的说明。
49.本发明实施例提供了一种微生物培养基优化方法，所述方法包括：
50.以培养基成分为自变量，以实验产物为响应变量进行均匀设计实验得到多个实验样本。
51.根据所述均匀设计实验采用偏最小二乘回归法构建各所述响应变量的plsr全模型，并将所述plsr全模型作为当前模型；所述plsr全模型为表示所述响应变量与所有所述自变量之间关系的二次多项式形式的数学表达式。
52.判断所述当前模型中是否所有自变量的vip得分均大于第一设定阈值，得到第一判断结果。
53.若所述第一判断结果为是，则将所述当前模型作为最终plsr模型，所述最终的plsr模型用于构建最优微生物培养基。
54.若所述第一判断结果为否，则以当前模型对应的显著性预测变量作为自变量构建各所述响应变量的vip-plsr模型，并将所述vip-plsr模型作为当前模型；所述显著性预测变量为vip得分大于第一设定阈值的自变量。
55.对各所述plsr全模型的决定系数和各所述vip-plsr模型的决定系数进行偏f检验，并判断是否存在统计学显著性差异，得到第二判断结果。
56.若所述第二判断结果为是，则将各所述当前模型作为最终的plsr模型。
57.若所述第二判断结果为否，则返回所述“判断所述当前模型中是否所有自变量的vip得分均大于第一设定阈值”的步骤。
58.在实际应用中，在所述根据所述均匀设计实验采用偏最小二乘回归法构建各所述响应变量的plsr全模型，并将所述plsr全模型作为当前模型之后还包括：
59.计算各所述plsr全模型的决定系数。
60.采用变量投影重要性技术对所述plsr全模型进行处理得到各自变量的vip得分。
61.在所述对各所述plsr全模型的决定系数和各所述vip-plsr模型的决定系数进行偏f检验，并判断各所述vip-plsr模型是否存在统计学显著性差异，得到第二判断结果之前还包括：
62.计算各所述vip-plsr模型的决定系数。
63.采用变量投影重要性技术对所述vip-plsr模型进行处理得到各显著性预测变量的vip得分。
64.在实际应用中，所述对各所述plsr全模型的决定系数和各所述vip-plsr模型的决定系数进行偏f检验具体为：
65.根据公式计算偏f检验值，其中，f
01
表示偏f检验值，表示plsr全模型的决定系数，表示第i轮vip-plsr模型的决定系数，n表示实验样本的数目，p表示模型中的自变量数目。
66.在实际应用中，所述第一设定阈值为0.8。
67.如图1所示，本发明实施例还提供了一种采用上述方法的更具体的实施方式：
68.进行培养基关键成分的均匀设计(ud)实验，并测量四种发酵产物的含量以获得建模样本，并分析自变量和因变量的相关系数及统计学显著性。
69.基于均匀设计数据集，以完全二次多项式为预设模型，建立培养基关键成分和发酵产物的偏最小二乘回归(plsr)模型，即plsr全模型，并计算决定系数r2和预测能力参数press
cv
。
70.根据偏最小二乘回归辅助技术变量投影重要性(vip)计算公式，计算完全回归模型中所有自变量的vip得分。
71.判断所有自变量的vip得分是否均大于或等于阈值0.8。
72.若为是则将plsr全模型确定为最终的plsr模型，并分析r2和预测能力参数press
cv
之间的线型相关性。
73.若为否则以vip得分大于或等于0.8的自变量为建模自变量，发酵产物作为建模因变量建立vip-plsr模型，计算自变量的vip得分和vip-plsr模型的决定系数r2和预测能力参数press
cv
，并进行plsr全模型和vip-plsr模型决定系数之间的偏f检验。
74.判断是否存在统计学显著性差异。
75.若是则将vip-plsr模型确定为最终的plsr模型分析r2和预测能力参数press
cv
之间的线型相关性。
76.若否则判断vip-plsr模型中所有自变量的vip得分是否都大于或等于0.8。
77.若是则将vip-plsr模型确定为最终的plsr模型，并分析r2和press之间的线性相关性。
78.若否，则返回“以vip得分大于或等于0.8的自变量为建模自变量，发酵产物作为建模因变量建立vip-plsr模型，计算自变量的vip得分和vip-plsr模型的决定系数r2和预测能力参数press
cv
，并进行plsr全模型和vip-plsr模型决定系数之间的偏f检验”。
79.最后，分析plsr全模型和vip-plsr模型的决定系数r2和预测能力参数press
cv
之间的线性相关关系，证明本发明所得简化模型不仅兼顾解释能力还能保证预测能力。
80.本发明实施例还提供了一种与上述方法对应的微生物培养基优化系统，所示系统包括：
81.实验模块，用于以培养基成分为自变量，以实验产物为响应变量进行均匀设计实验得到多个实验样本。
82.plsr全模型构建模块，用于根据所述均匀设计实验采用偏最小二乘回归法构建各所述响应变量的plsr全模型，并将所述plsr全模型作为当前模型；所述plsr全模型为表示所述响应变量与所有所述自变量之间关系的二次多项式形式的数学表达式。
83.第一判断模块，用于判断所述当前模型中是否所有自变量的vip得分均大于第一设定阈值，得到第一判断结果。
84.第一最终模型确定模块，用于若所述第一判断结果为是，则将所述当前模型作为最终plsr模型，所述最终的plsr模型用于构建最优微生物培养基。
85.vip-plsr模型构建模块，用于若所述第一判断结果为否，则以当前模型对应的显著性预测变量作为自变量构建各所述响应变量的vip-plsr模型，并将所述vip-plsr模型作为当前模型；所述显著性预测变量为vip得分大于第一设定阈值的自变量。
86.偏f检验模块，用于对各所述plsr全模型的决定系数和各所述vip-plsr模型的决定系数进行偏f检验，并判断是否存在显著性差异，得到第二判断结果。
87.第二最终模型确定模块，用于若所述第二判断结果为是，则将各所述当前模型作为最终的plsr模型。
88.循环模块，用于若所述第二判断结果为否，则返回所述“判断所述当前模型中是否所有自变量的vip得分均大于第一设定阈值”的步骤。
89.作为一种可选的实施方式，所述微生物培养基优化系统，还包括：
90.plsr全模型决定系数计算模块，用于计算各所述plsr全模型的决定系数。
91.plsr全模型自变量vip得分确定模块，用于采用变量投影重要性技术对所述plsr全模型进行处理得到各自变量的vip得分。
92.作为一种可选的实施方式，所述微生物培养基优化系统，还包括：
93.vip-plsr模型决定系数确定模块，用于计算各所述vip-plsr模型的决定系数。
94.vip-plsr模型自变量vip得分确定模块，用于采用变量投影重要性技术对所述vip-plsr模型进行处理得到各显著性预测变量的vip得分。
95.作为一种可选的实施方式，所述偏f检验模块具体为：
96.根据公式计算偏f检验值，其中，f
01
表示偏f检验值，表示plsr全模型的决定系数，表示第i轮vip-plsr模型的决定系数，n表示实验样本的数目，p表示模型中的自变量数目。
97.本发明实施例还提供了更具体的微生物培养基优化方法，所述方法整合一系列策略，即采用留一法交叉验证提取潜变量、利用r2和press
cv
分别评价模型的拟合优度和预测
能力，使用vip技术评估自变量的重要性，构建偏f检验评估删除不显著性预测变量对模型拟合优度和预测能力的影响，成功构建了简约，稳健且预测精度高的数学模型，其具体技术方案为：
98.步骤1：基于的均匀设计实验，并为后续研究提供建模样本数据。对mgcl2·
6h2o，cysteine hydrochloride和cacl2·
2h2o三种培养基成分(自变量)，按均匀设计要求进行热纤梭菌培养实验(表1)，并分别测定培养液生物量(od
600
)、乳酸根浓度、乙酸根浓度和乙醇浓度，并作为响应变量。该步骤将为步骤2中的plsr建模提供样本。
99.接着用二次多项式(公式1)表征培养基均匀设计配比和响应变量之间的数学关系，设定了培养基成分和响应变量间的二次多项式模型，最后用皮尔逊相关系数法分析培养基配比和响应变量组合矩阵的两两变量间的相关系数，并进行相关系数的显著性检验(为了说明自变量之间相关性，也就是前文提到的共线性)。
[0100][0101]
其中，β0是截距项，βi是线性项系数，β
ii
是平方项系数，β
ij
是交叉项系数(i≠j)，ε是模型误差项。y是响应变量的代号。xi和xj都是自变量，也就是培养基成分。ε是实验误差。
[0102]
步骤2：在步骤1均匀设计样本数据的基础上，建立各响应变量的plsr全模型。
[0103]
利用“留一法”交叉验证筛选合适的潜变量，相关计算公式如下所示：
[0104][0105]
yi是响应变量y的第i观测值，观测值的意思就是实验值。其中n为建模样本数目，是响应变量y在排除第i个样本而利用剩余样本提取h个潜变量进行回归建模模型情况下的拟合值即利用plsr回归分析得出的理论值(根据公式1得到的)，pressh是响应变量y的“留一法”预测误差平方和，是响应变量y基于全部样本提取h-1个潜变量进行plsr建模的第i个拟合值，ss
h-1
是相应的误差平方和，根据交叉检验基本准则，当是相应的误差平方和，根据交叉检验基本准则，当时，增加新的潜变量有助于降低模型预测误差，反之亦然。在确定提取潜变量的最佳数目之后，建立包含所有自变量的plsr全模型(二次多项式回归方程)，并计算决定系数r2。
[0106]
此外，交叉验证均方根差press
cv
常用于评价plsr全模型的预测能力，即press
cv
越小，plsr全模型的预测能力越强，其计算公式为
[0107][0108]
其中press为预测误差平方和，而n表示建模样本数目。该步骤通过交叉验证基本规则建立了四个响应变量的全模型plsr，一个全模型对应一个响应变量，并得出了相应的回归方程和反映模型预测能力的关键参数press
cv
，并为后续vip-plsr的建立，提供了蓝本。
[0109]
步骤3：计算各响应变量的plsr全模型中自变量的vip数据。利用vip技术评估自变量对响应变量的重要程度，即通过vip得分的大小衡量，建模自变量j的vip得分vipj的计算公式如下：
[0110][0111]
其中p代表建模自变量数目，th代表观测矩阵x提取的第h个潜变量，代表响应变量y和第h个潜变量间的相关系数，该系数表征了第h个潜变量对响应变量y的解释能力，w
hj
代表第j个自变量对第h个潜变量的权重，且通过nipals算法计算权重值，vip＝0.8表示自变量对响应变量具有显著作用的阈值，由此建立自变量矩阵对响应变量的vip得分矩阵。该步骤获得的响应变量的plsr全模型中自变量的vip数据将为后续vip-plsr模型的建立，提供变量重要性筛选蓝本。观测矩阵一般指实验设计中自变量纵横组合构成的矩阵，其中矩阵的每一行代表一个实验组和，或者实验样本，行数就是样本数目，本发明总共8组实验样本，每一列表示某一自变量(本文为培养基成分及其平方项和交叉项)数量在样本中的变化情况，或者说水平数，本文自变量有四种变化，或者说四种水平数。
[0112]
步骤4：基于变量投影重要性迭代回归的plsr(即vip-plsr模型)的建立。
[0113]
主要是整合基于偏f检验的vip变量筛选技术和稳健的判定系数准则，即首先利用步骤3筛选的显著性预测变量(vip得分≥0.8)，作为新的输入自变量，对响应变量进行新一轮的plsr建模，得到vip-plsr模型。
[0114]
一般认为线性模型的拟合优度(以决定系数r2表示，下同)会随着自变量数量的增加而增加，随着删除冗余变量的逐步删除而逐渐降低，这将降低模型的拟合精度，甚至影响预测精度。虽然本发明的vip-plsr模型本质是非线性模型，但也是拟线性模型，因此也必须考虑这方面的影响，所以必须做出权衡：即保证删除冗余自变量后留下的自变量的vip得分≥0.8，还需保证变量筛选过程不严重破坏plsr模型的拟合优度(即采用稳健的拟合优度策略)，所以通过构建假设性偏f检验以科学衡量vip筛选过程中，删除vip值较小的自变量，是否影响模型的解释能力来实施。偏f检验构建过程如下：
[0115]
plsr全模型和第一轮vip回归的决定系数分别表示为和其差值定义为公式(5)
[0116][0117]
若接近于0，表示利用vip技术删除自变量，不影响对响应变量的拟合优度，反之亦然。由此构建偏f检验模型：
[0118][0119]
其中n是样本数目，p是建模自变量数目。当f
01
～f(1，n-p-1)，根据显著水平α＝0.05查表得到拒绝域的临界值f
α
，得到下面的决策准则：
[0120]
1)如果f
01
》f
0.05
时，显著不等于0，说明利用vip技术删除不显著性预测变量已显著降低响应变量的解释能力所以将vip-plsr模型确定为最终的plsr模型。
[0121]
2)如果f
01
≤f
0.05
，显著为0，说明利用vip技术删除不显著性预测变量不会显著降低响应变量的解释能力，则进入下一轮(重复步骤3和4)，plsr全模型和其他轮vipi模型(i＝2，3，4...)之间的偏f检验以此类推。
[0122]
最后，每个响应变量的vip-plsr建模中，均发现每轮vip模型的多个决定系数r2和响应的press
cv
之间都存在一定的负相关关系，即r2越大，press
cv
越小，模型预测能力越强。为定量刻画二者间的关系，对每一响应变量及四个响应变量的集合均建立press
cv
对r2的线性回归模型。该步骤基于交叉验证准则、偏f检验的vip变量筛选技术和稳健的判定系数准则，建立响应变量的vip-plsr模型，获得相应的偏f检验结果、回归方程和r2变化情况等信息，从而不仅为后续实验验证提供了预测方程，还明确了vip-plsr模型删除冗余自变量后，模型得以大幅度简化，但并不显著降低拟合优度，拟合优度还存在随着冗余变量被剔除而反常增大的情况，疑与二次多项式本质是非线性模型有关。还新发现反映plsr全模型和vip-plsr模型拟合优度的r2和预测能力的press
cv
之间存在明显的负线性关系，因此基于r2变化情况的偏f检验不仅可以反映模型的拟合优度，还能反映其预测能力。
[0123]
步骤5：模型的求解与验证。利用octave软件包中多元非线性约束问题求解函数fmincon对生物量、乙酸、乳酸和乙醇的plsr全模型和最终优化好的vip回归模型(vip-plsr模型)进行求解，得出相应的最优解(培养基最佳预测配比)和最优值(响应变量最佳预测值)，分别在各自培养基最佳预测配比条件下进行验证实验，并比较两种模型预测值与实验值的相对误差，以考察两种模型的预测精度，及确定vip-plsr模型对全模型的简化效果得到本发明的vip-plsr模型效果更好。
[0124]
本发明还提供了采用上述培养基优化方法来提高热纤梭菌的乙醇耐受性的实施例：
[0125]
1.实验材料与测定方法
[0126]
菌株：热纤梭菌atcc35609耐受株，即耐受3％(v/v)的外源乙醇，gs-2培养基为初始培养基，培养方法：60℃厌氧(充入10％co2，5％h2和85％n2维持厌氧环境)静置培养，培养48h后，利用比浊法测定菌体生物量，利用高效色谱法(hplc)培养液乳酸浓度、乙酸浓度和乙醇浓度。
[0127]
2.均匀设计实验
[0128]
依据plackett
–
burman实验，mops、酵母粉、柠檬酸钠和纤维二糖浓度分别设定为5、7、3和10g/l，kh2po4、k2hpo4，尿素和feso4·
7h2o浓度分别设定为1、3.5、2g/l和1.25mg/l，初始ph设定为7.4。对三种关键成分mgcl2·
6h2o，cacl2·
2h2o和半胱氨酸盐酸盐，依据均匀设计表u8(45)安排实验，相应的发酵响应见表1所示。
[0129]
表1均匀设计及实验结果
[0130][0131][0132]ax1，x2和x3分别代表培养基成分mgcl2·
6h2o，cysteine hydrochloride和cacl2·
2h2o。其余表格代码相同。
[0133]
由表1知，均匀设计培养基配比组合重构了细胞代谢网络，导致细菌生物量和培养液三种关键代谢物都发生了改变。其中5号实验生物量最大，达到3.13
±
0.142，比初始培养基提高198.38％。这说明培养基优化初步成功，并且可以进行进一步的建模优化。但若采用公式(1)进行基于最小二乘的二次多项式回归建模，需要的实验次数至少为1+3
×
(3+3)/2＝10，而目前实验次数仅为8，属于小样本问题，所以只能采用偏最小二乘等，而不能采用基于最小二乘的方法建立回归模型。
[0134]
分析基于均匀设计的二次多项式回归模型变量间的皮尔逊相关系数，并用t检验分析相关系数的显著性，结果如表2：
[0135]
表2均匀设计的相关系数矩阵及显著性检验
[0136][0137][0138]ay1，y2，y3和y4分别代表生物量，乳酸，乙酸和乙醇，下同。
[0139]“*”：相关系数在α＝0.1水平上显著(t检验，r为皮尔逊相关系数，双尾概率，下同)。
[0140]“**”：相关系数在α＝0.05水平上显著。
[0141]“***”：相关系数在α＝0.01水平上显著。
[0142]
由表2知，自变量之间，自变量与响应变量之间，响应变量与响应变量之间存在多
种共线性，有些甚至是极显著相关的，例如r(x1，y2)＝0.931；r(y1，y3)＝0.985等。这也说明本发明涉及的均匀设计回归建模只能采用偏最小二乘等，而不能采用基于最小二乘的方法，否则模型稳健性和预测能力差。
[0143]
3.plsr全模型的建立
[0144]
利用公式(3)进行基于“留一法”交叉验证的潜变量提取，结果见表3所示。
[0145]
表3基于“留一法”交叉验证(vip
threshold
＝0.80)vip迭代回归建模潜变量的提取情况
[0146]
[0147][0148]a第i(i＝1，2，3，4)个响应变量第j(j＝0，1，2，3，
…
)轮vip自变量筛选回归，其中，“0”轮即为plsr全模型，下表同。
[0149]
由表3易知，所有四个响应变量的plsr全模型建模，均只需提取一个主成分，即可达到交叉验证的基本判别标准，若再多提取一个潜变量，将变成负值，不利于模型预测能力的提高。合理提取潜变量后，plsr全模型将成功建立，具体参见表4。易知所有四个响应变量都产生相当好的回归模型，均具有相当好的决定系数，即r2均大于0.9。且计算得出四个响应变量回归模型自变量的vip得分，具体见图2，其中图2(a)为plsr全模型和vip-plsr模型对生物量(od
600
)的预测结果图，图2(b)为plsr全模型和vip-plsr模型对乳酸根(g/l)的预测结果图，图2(c)为plsr全模型和vip-plsr模型对乙酸根(g/l)的预测结果图，图2(d)为plsr全模型和vip-plsr模型对乙醇(g/l)的预测结果图，易知自变量x2、x3、x1x2和x1x3是响应变量y1筛选出来的显著性预测变量。
[0150]
表4基于的vip-plsr建模过程
[0151]
[0152]
[0153][0154]avip
10
，vip
20
，vip
30
和vip
40
分别对应响应变量y1，y2，y3和y4的全模型。
[0155]b“‑”
表示对应自变量不参与回归建模，属于被删除的不显著性预测变量。
[0156]c加粗数字表示相应自变量的vip得分大于等于0.8(依据图2)。
[0157]dλ表示第j(j＝0，1，2，3，
…
)轮vip-plsr模型决定系数对其全模型(vip0)决定系数的比值。
[0158]
4.基于迭代回归的vip-plsr模型的建立
[0159]
分别利用四个响应变量全模型筛选出的显著性预测变量(vip得分≥0.8)，作为新的输入自变量，分别对响应向量进行新一轮的plsr建模，即依次利用公式(2)提取潜变量，利用公式(3)计算press
cv
，利用公式(4)计算回归模型中自变量的vip得分，利用公式(5)进行偏f检验，以分析删除vip得分≤0.8的自变量是否显著降低模型的拟合优度，随后也建立相应的二次多项式回归模型。经过一定轮数的循环，直到模型中所有的自变量都是显著变量，相应结果分别见表3，表4和图2。由表3可知，除了vip
21
提取2个潜变量达到交叉验证条件之外，其他所有四个响应变量的vip-plsr建模，均只需提取一个主成分，即可达到交叉验证的基本判别标准，若再多提取一个潜变量，将变成负值，不利于模型预测能力的提高。
[0160]
合理提取潜变量后，vip-plsr回归模型得以建立(表4)，易知经过有限次vip循环建模后，所有四个响应变量的自变量均为显著变量，即vip得分大于0.8，例如响应变量y1和y2，即生物量和乳酸分别经过两轮和四轮vip循环达到预定目标(图2)。并且vip-plsr的所有决定系数r2均均无统计学显著性差异，也就是删除不显著性预测变量后，并不会显著影响模型的拟合优度。由此回归模型得以大幅度简化，提高了模型的稳健性和可解释性，例如对于响应变量y1的vip-plsr建模，自变量的数目精简情况是：9(vip
10
，全模型)
→
6(vip
11
，即第一轮)
→
4(vip
12
，即第二轮)。奇特的是回归模型的决定系数r2并没有随着建模自变量数目的减少而单调降低，而是存在一定的波动情况，例如对于响应变量y1，r2变化如下：0.9743(vip
10
，全模型)
→
0.8914(vip
11
，即第一轮vip-plsr)
→
0.9553(vip
12
，即第二轮vip-plsr)。更奇特的是vip
21
由于提取了两个潜变量，其决定系数r2居然是全模型的105.64％。该奇特现象有悖于传统线性模型决定系数r2随着自变量数目增加而变大的一般规律，疑与拟线性偏最小二乘的非线性性质有关。此外，press
cv
对相应模型决定系数r2的线性回归结果如图3和图4所示，其中图3(a)为生物量，图3(b)为乳酸根，图3(c)为乙酸根，图3(d)为乙醇，其中图4(a)为vip-plsr建模过程中生物量press
cv
与r2拟合的结果图，图4(b)为vip-plsr建模过程中乳酸根press
cv
与r2拟合的结果图，图4(c)为vip-plsr建模过程中乙酸根press
cv
与r2拟合的结果图，图4(d)为vip-plsr建模过程中乙醇press
cv
与r2拟合的结果图，其中vip数值大于0.8表示自变量对响应变量影响显著。vip
ij
(i＝1，2，3
…
，j＝0，1，2，3)表示第i响应变量的第j轮vip筛选，而vip
10
，vip
20
，vip
30
和vip
40
分别对应响应变量y1，y2，y3和y4的全模型。易
知无论是每一个响应变量还是四个响应变量的组合，press
cv
和r2均呈现明显的负线性关系，且线性模型的决定系数均超过95％，这说明r2越大，press
cv
越小，即模型预测能力越强，因此公式(5)构建的利用vip变量筛选技术进行的基于r2变化情况的偏f检验，不仅可以评估模型的拟合情况，还能评价其预测能力，而此前文献中并未报道这种情况。
[0161]
由图3知，随着vip-plsr建模的进行，所有自变量的vip得分均逐渐下降，最终保留在模型的自变量的vip得分均≥0.8，并且vip得分大小变得更加平衡，例如响应变量y1全回归模型(vip
10
)的vip得分的波动范围是从0.4931到1.4519，而vip
12
的vip得分的波动范围仅从0.8336到1.1149。然而自变量的均衡化，并不意味着其重要性的均衡化，因为虽然所有自变量的vip得分均随着vip-plsr建模的进行而逐渐下降，但是由表4可知，除个别特殊情况，例如vip
21
等之外，自变量对应的回归系数的绝对值却普遍增加了，比较典型的是响应变量y1，虽然自变量的vip值均下降，但是其回归系数的绝对值却显著增加。
[0162]
5.模型的求解与验证
[0163]
通过octave软件包中多元非线性约束问题求解函数fmincon，对生物量、乙酸浓度、乳酸浓度和乙醇浓度的plsr全模型和vip模型进行求解，相应结果见表5所示。有趣的是，除了乳酸外，其余三个响应变量的plsr全模型和vip-plsr模型均预测了相同的最优培养基配比，这证明了对全模型进行简化的必要性和vip模型稳健性，而相应的预测最优值却有差异。然而验证实验结果表明，四个响应变量全模型和vip-plsr模型预测的相对误差均小于5％，且除了第一个响应变量生物量和第四个响应变量乙醇之外，后者的整体预测精度大于前者，这说明vip-plsr模型的泛化能力强一些，虽然回归模型已大大简化，但是并未影响预测精度。
[0164]
表5响应变量全模型和vip-plsr模型优化结果和实验验证
[0165][0166]
通过本实施例不仅证明了本发明提出的vip-plsr回归方法可建立简约，稳健且预测精度高的模型，并且还证明了1)本发明提出的vip-plsr模型由于非线性特征，打破了传统线性模型减少自变量必然降低模型拟合优度的弊端，也就是新模型可以兼顾精简度和拟合优度；2)本发明新发现vip-plsr模型的拟合优度和预测能力呈现正比关系，从而可以通
过基于考察拟合优度(以决定系数r2表示)下降的偏f检验，在删除冗余自变量的同时，保证了模型具有较好的拟合优度和预测能力。
[0167]
本说明书中各个实施例采用递进的方式描述，每个实施例重点说明的都是与其他实施例的不同之处，各个实施例之间相同相似部分互相参见即可。对于实施例公开的系统而言，由于其与实施例公开的方法相对应，所以描述的比较简单，相关之处参见方法部分说明即可。
[0168]
本文中应用了具体个例对本发明的原理及实施方式进行了阐述，以上实施例的说明只是用于帮助理解本发明的方法及其核心思想；同时，对于本领域的一般技术人员，依据本发明的思想，在具体实施方式及应用范围上均会有改变之处。综上所述，本说明书内容不应理解为对本发明的限制。