一种基于数据驱动的磁控胶囊指向控制方法

1.本发明涉及一种基于数据驱动的磁控胶囊指向控制方法，以满足胶囊机器人系统实现对目标区域的高精度指向以及削弱控制抖振的性能要求。


背景技术：

2.随着肠胃检测在医学领域的需求不断增加，内窥镜技术也在不断地改革创新。传统医用内窥镜通过口腔进入体内以完成对肠胃病变区域的观察，但是在使用传统内窥镜检查时，由于内窥镜结构较为复杂，操作繁琐，同时可能会对患者造成物理上的伤害，患者需要承受其带来的疼痛。因此，为了解决传统内窥镜所存在的问题，取而代之的胶囊机器人逐渐发展起来。近几年，国内外学者对主动控制的胶囊机器人进行了较多研究，在各方面取得了一定成果，但是胶囊机器人仍处于初期发展阶段，各学者对胶囊机器人的研究在结构和控制策略等方面均存在着差异和不足。因此，研究胶囊机器人的主动控制以及实现胶囊机器人的位移和调姿等一系列运动对于胶囊机器人的发展具有重要价值。
3.然而，由于胶囊机器人控制系统是典型的多变量、强耦合、非线性系统，控制胶囊机器人的位移和指向角度，使之实现各种运动会遇到许多复杂的难题。例如，测量和建模的精度达不到要求，再加上外部负载扰动及非结构环境下的摩擦变化等不确定因素的影响，导致无法获得满足胶囊机器人精确、完整的动力学模型。因此，如pd控制、计算力矩法控制等常规的胶囊机器人控制策略和算法已经无法满足胶囊机器人应用领域的控制要求。
4.在mpc或者其他控制器设计的时候常使用一阶滤波来进一步提高控制品质。例如，对被控变量的实测值进行滤波，可以避免测量噪声或测量波动导致控制器作用过于频繁；对定值进行柔化，可以避免设定值导致求解得到的控制作用过于激进而使系统的超调较大。因此，将一阶滤波应用于胶囊机器人系统，具有重要的理论和实际意义。


技术实现要素：

5.为了克服现有技术的不足，针对具有多变量、强耦合以及扰动等不确定性的胶囊机器人系统，利用两相幂次趋近律能够提高被控变量的瞬态收敛速度和减小被控变量进入稳态时的控制抖振。同时，基于两相幂次趋近律设计一阶滤波器，保证控制信号的连续性和削弱因符号函数导致的控制抖振问题。
6.为了解决上述技术问题提出的技术方案如下：
7.一种基于数据驱动的磁控胶囊指向控制方法，包括以下步骤：
8.步骤1，建立胶囊机器人系统的动态模型，初始化系统状态以及控制参数，过程如下：
9.1.1记胶囊中心位置为[x,y,z]，根据坐标变换，胶囊中任意一点的坐标c的表达形式为：
[0010][0011]
其中，l表示胶囊的实际长度；ψ表示胶囊绕z轴的旋转角度；θ表示胶囊绕x轴的旋转角度；表示胶囊绕y轴的旋转角度；
[0012]
1.2胶囊机器人系统的动能和势能之和l的表达式为：
[0013][0014]
其中，2r表示胶囊的理想长度；m表示胶囊的总质量；
[0015]
考虑到胶囊机器人绕z轴的旋转速度较慢，令其指向角度q＝[θ φ]
t
，根据拉格朗日动力学方程，得到胶囊模型表达式为：
[0016][0017][0018][0019]
g＝[0 0]
t
ꢀꢀꢀ
(6)
[0020]
其中，b、c、g分别为惯性矩阵、科里奥利矩阵和重力矩阵；分别表示为指向角度q的二阶和一阶微分；τ表示作用在系统上的总力矩；
[0021]
步骤2，基于存在未知动态的胶囊机器人系统，定义其跟踪误差和扰动，设计控制器，过程如下：
[0022]
2.1定义系统的跟踪误差：
[0023]
e＝q-qdꢀꢀꢀ
(7)
[0024]
其中，qd表示胶囊的期望指向角度；
[0025]
定义系统中存在的扰动：
[0026][0027]
其中，a、b表示两个任意的给定参数；表示a、b的最大值；
[0028]
则基于式(3)，系统的模型表达式表示为：
[0029][0030]
其中，q表示qs中的一个被控量、b1，c1，g1表示q的相关参数；
[0031]
2.2设计一阶滤波器：
[0032][0033]
对式(10)求导得：
[0034]
[0035]
其中，λ＞0，分别表示指向角度误差e的一阶和二阶微分；
[0036]
2.3设计两相幂次趋近律：
[0037][0038]
其中，ρ＞0，η＞0，p1、p2、q1、q2均为正奇数，且p1＞q1＞0，p2＞q2＞0；
[0039]
联立式(11)、(12)得：
[0040][0041]
将τ设计为：
[0042][0043]
联立式(13)、(14)得：
[0044][0045]
本发明的技术构思为：首先，两相幂次趋近率用以调节被控变量的收敛速度，使其在到达减速点之前具有较快的收敛速度，而在到达减速点以后，则能有效地削弱抖振；在此基础上，设计一阶滤波器，保证系统指向角度输出能够快速稳定地跟踪期望指向角度。
[0046]
本发明的有益效果为：两相幂次趋近律形式保证系统输出具有较好的瞬态和稳态性能。一阶滤波器补偿不确定项对系统跟踪精度的影响，增强了系统的鲁棒性。同时，由于设计中不包含不连续函数，因此能够保证控制信号的连续性和减小抖振问题。
附图说明
[0047]
图1为胶囊机器人系统的指向角度跟踪效果示意图(以绕x轴指向为例)，其中红色虚线代表期望指向角度，蓝色实线代表基于数据驱动的磁控胶囊指向控制方法的系统实际指向角度。
[0048]
图2为胶囊机器人系统的总力矩变化示意图，其中蓝色实线代表基于数据驱动的磁控胶囊指向控制方法的系统力矩变化。
[0049]
图3为胶囊机器人系统的被控变量收敛过程，其中蓝色实线代表基于数据驱动的磁控胶囊指向控制方法的控制器变量的收敛过程。
[0050]
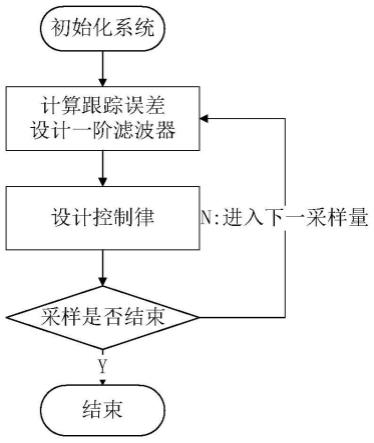
图4为本发明的控制流程示意图。
具体实施方式
[0051]
下面结合附图对本发明做进一步说明。
[0052]
参照图1-图4，一种基于数据驱动的磁控胶囊指向控制方法，包括以下步骤：
[0053]
步骤1，建立胶囊机器人系统的动态模型，初始化系统状态以及控制参数，过程如下：
[0054]
1.1记胶囊中心位置为[x,y,z]，根据坐标变换，胶囊中任意一点的坐标c的表达形
式为：
[0055][0056]
其中，l表示胶囊的实际长度；ψ表示胶囊绕z轴的旋转角度；θ表示胶囊绕x轴的旋转角度；表示胶囊绕y轴的旋转角度；
[0057]
1.2胶囊机器人系统的动能和势能之和l的表达式为：
[0058][0059]
其中，2r表示胶囊的理想长度；m表示胶囊的总质量；
[0060]
考虑到胶囊机器人绕z轴的旋转速度较慢，令其指向角度q＝[θ φ]
t
，根据拉格朗日动力学方程，得到胶囊模型表达式为：
[0061][0062][0063][0064]
g＝[0 0]
t
ꢀꢀꢀ
(18)
[0065]
其中，b、c、g分别为惯性矩阵、科里奥利矩阵和重力矩阵；分别表示为指向角度q的二阶和一阶微分；τ表示作用在系统上的总力矩；
[0066]
步骤2，基于存在未知动态的胶囊机器人系统，定义其跟踪误差和扰动，设计控制器，过程如下：
[0067]
2.1定义系统的跟踪误差：
[0068]
e＝q-qdꢀꢀꢀ
(19)
[0069]
其中，qd表示胶囊的期望指向角度；
[0070]
定义系统中存在的扰动：
[0071][0072]
其中，a、b表示两个任意的给定参数；表示a、b的最大值；
[0073]
则基于式(3)，系统的模型表达式表示为：
[0074][0075]
其中，q表示qs中的一个被控量、b1，c1，g1表示q的相关参数；
[0076]
2.2设计一阶滤波器：
[0077][0078]
对式(10)求导得：
[0079][0080]
其中，λ＞0，分别表示指向角度误差e的一阶和二阶微分；
[0081]
2.3设计两相幂次趋近律：
[0082][0083]
其中，ρ＞0，η＞0，p1、p2、q1、q2均为正奇数，且p1＞q1＞0，p2＞q2＞0；
[0084]
联立式(11)、(12得：
[0085][0086]
将τ设计为：
[0087][0088]
联立式(13)、(14)得：
[0089][0090]
为了更有效的进行仿真，胶囊机器人系统模型参数设置为r＝1cm，m＝0.01kg。系统初值设置为θ＝0cm，τ＝0。期望指向角度设置为θd＝5，一阶滤波器增益设置为λ＝3。干扰系数a＝1，b＝1。
[0091]
图1为胶囊机器人系统的指向角度跟踪效果示意图(以绕x轴指向为例)，可以看出系统的指向角度跟踪速度较快，瞬态性能较好。图2为胶囊机器人系统的总力矩变化示意图，从图中可以看出系统总力矩具有较快的趋近速度。图3为胶囊机器人系统的滑模变量收敛过程图。另外，控制器设计中削弱采用符号函数，保证了控制器连续，因此，抖振被削弱。
[0092]
以上阐述的是本发明给出的一个实施例表现出的优良优化效果，显然本发明不只是限于上述实施例，在不偏离本发明基本精神及不超出本发明实质内容所涉及范围的前提下对其可作种种变形加以实施。