预测存活概率的方法及相关设备

1.本技术涉及风险预测技术领域，尤其涉及一种预测存活概率的方法及相关设备。


背景技术：

2.5g自商用部署以来受到广泛关注，5g赋能行业的应用是现在及未来移动互联网的重要研究方向，推动着各类垂直行业的发展，旨在为任何类型的设备在任何应用场景提供更实时可靠的连接，实现支撑和引领社会进一步网络化和智能化的目标。6g将在5g基础上全面支持整个世界的数字化，并结合大数据、人工智能等技术的发展，实现智慧的泛在可取、全面赋能万事万物，推动社会走向虚拟与现实结合的“数字孪生”世界，通信网络实现“数字孪生，智慧泛在”的美好愿景。围绕这一总体愿景，6g网络将在智享生活、智赋生产、智焕社会三个方面催生全新的应用场景，比如孪生数字人、全息交互、超能交通、通感互联、智能感知交互等。
3.5g下的大规模机器通信在6g时代的一个重要延伸方向就是从机器与机器的通信发展到机器与人的通信，再到个性化人机通信。以感知-通信一体化网络为基础的以人为本的服务(hcs)值得被进一步研究。以人为本服务在大健康场景下的发展方向已经从研究对可穿戴设备和植入式设备在患者身上的应用，逐步转变为注重对患者或者正常人体生命体征的预测，例如对潜在疾病和对自然寿命的预测，进而应用到诸如智慧养老的新场景中，数据在可量化的层面，孪生出可信情况。更准确的表征个体自然死亡概率的不确定性，能够实现现实到虚拟，实际到估计的相互可信映射，更准确的使感知-通信一体化技术赋能到个人的生活当中。
4.但现有的预测存活概率的方法及相关设备只能粗略的度量存活概率，并不能很准确的描述个体死亡的随机性，也不能描述个体死亡风险的差异性与不确定性。


技术实现要素：

5.有鉴于此，本技术的目的在于提出一种预测存活概率的方法及相关设备。基于上述目的，本技术提供了一种预测存活概率的方法，其特征在于，包括：
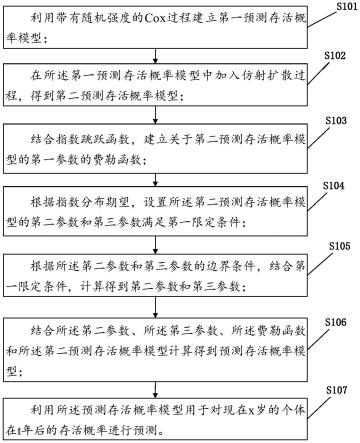
6.利用带有随机强度的cox过程建立第一预测存活概率模型；
7.在所述第一预测存活概率模型中加入仿射扩散过程，得到第二预测存活概率模型；
8.结合指数跳跃函数，建立关于第二预测存活概率模型的第一参数的费勒函数；
9.根据指数分布期望，设置所述第二预测存活概率模型的第二参数和第三参数满足第一限定条件；
10.根据所述第二参数和第三参数的边界条件，结合第一限定条件，计算得到第二参数和第三参数；
11.结合所述第二参数、所述第三参数、所述费勒函数和所述第二预测存活概率模型计算得到预测存活概率模型；利用所述预测存活概率模型用于对现在x岁的个体在t年后的
存活概率进行预测。
12.在一种可能的实现方式中，所述第一预测存活概率模型具体为：
[0013][0014]
其中，s
x
(t)表示x岁的个体在t年后的存活概率，t
x
表示x岁的个体的未来寿命时间，表示t＝0，λs表示时间为s时的非负死亡力强度函数。
[0015]
在一种可能的实现方式中，所述仿射扩散过程满足以下公式：
[0016]
dx
t
＝μ(x
t
,t)dt+σ(x
t
,t)db
t
[0017]
其中，x
t
表示仿射扩散过程，μ(
·
)表示仿射扩散结构，σ(
·
)表示仿射扩散结构，b
t
表示布朗运动。
[0018]
在一种可能的实现方式中，所述费勒函数具体为：
[0019][0020]
其中，λ
x
(t)表示所述第一参数，a表示常数，ε表示波动率参数，w
t
表示带有波动率的死亡力强度函数，j(t)表示指数跳跃函数。
[0021]
在一种可能的实现方式中，所述第一限定条件具体为：
[0022][0023]
其中，α
′
(t)表示第二参数的微分，β
′
(t)表示第三参数的微分，β(t)表示所述第三参数，l表示跳跃强度，a表示常数，μ表示仿射扩散结构，σ表示仿射扩散结构。
[0024]
在一种可能的实现方式中，所述第二参数和第三参数的边界条件，包括：
[0025]
变量为0时，所述第二参数和所述第三参数均为0。
[0026]
在一种可能的实现方式中，所述第二参数和所述第三参数为：
[0027][0028]
其中，α(t)表示第二参数，β(t)表示第三参数，l表示跳跃强度，μ表示仿射扩散结构，a、b、c、d均为常数。
[0029]
基于同一发明构思，本技术实施例还提供了一种建立预测不确定性事件模型的装置，包括：
[0030]
建立模块，被配置为利用带有随机强度的cox过程建立第一预测存活概率模型；
[0031]
仿射扩散模块，被配置为在所述第一预测存活概率模型中加入仿射扩散过程，得到第二预测存活概率模型；
[0032]
建立模块，被配置为结合指数跳跃函数，建立关于第二预测存活概率模型的第一参数的费勒函数；
[0033]
设置模块，被配置为根据指数分布期望，设置所述第二预测存活概率模型的第二
参数和第三参数满足第一限定条件；
[0034]
计算模块，被配置为根据所述第二参数和第三参数的边界条件，结合第一限定条件，计算得到第二参数和第三参数；
[0035]
计算模块，被配置为结合所述第二参数、所述第三参数、所述费勒函数和所述第二预测存活概率模型计算得到预测存活概率模型；利用所述预测存活概率模型用于对现在x岁的个体在t年后的存活概率进行预测。
[0036]
基于同一发明构思，本技术实施例还提供了一种电子设备，包括存储器、处理器及存储在存储器上并可在处理器上运行的计算机程序，其特征在于，所述处理器执行所述程序时实现如上述任意一项所述的预测存活概率的方法。
[0037]
基于同一发明构思，本技术实施例还提供了一种非暂态计算机可读存储介质，所述非暂态计算机可读存储介质存储计算机指令，其特征在于，所述计算机指令用于使计算机执行上述任意一项所述的预测存活概率的方法。
[0038]
从上面所述可以看出，本技术提供的预测存活概率的方法及相关设备，通过利用带有随机强度的cox过程建立第一预测存活概率模型；在所述第一预测存活概率模型中加入仿射扩散过程，得到第二预测存活概率模型；结合指数跳跃函数，建立关于第二预测存活概率模型的第一参数的费勒函数；根据指数分布期望，设置所述第二预测存活概率模型的第二参数和第三参数满足第一限定条件；根据所述第二参数和第三参数的边界条件，结合第一限定条件，计算得到第二参数和第三参数；结合所述第二参数、所述第三参数、所述费勒函数和所述第二预测存活概率模型计算得到预测存活概率模型；利用所述预测存活概率模型用于对现在x岁的个体在t年后的存活概率进行预测。对于存活概率这一具有随机性的不确定问题，通过建立预测存活概率模型对其进行显式化表达，提高了模型的鲁棒性与准确度。
附图说明
[0039]
为了更清楚地说明本技术或相关技术中的技术方案，下面将对实施例或相关技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本技术的实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。
[0040]
图1为本技术实施例的预测存活概率的方法流程图；
[0041]
图2为本技术实施例的1922年出生的65岁女性预测存活概率与实际存活概率对比示意图；
[0042]
图3为本技术实施例的1922年出生的65岁男性预测存活概率与实际存活概率对比示意图；
[0043]
图4为本技术实施例的1932年出生的65岁女性预测存活概率与实际存活概率对比示意图；
[0044]
图5为本技术实施例的1932年出生的65岁男性预测存活概率与实际存活概率对比示意图；
[0045]
图6为本技术实施例的1942年出生的65岁女性预测存活概率与实际存活概率对比示意图；
[0046]
图7为本技术实施例的1942年出生的65岁男性预测存活概率与实际存活概率对比示意图；
[0047]
图8为本技术实施例的预测存活概率的装置结构图示意图；
[0048]
图9为本技术实施例的预测存活概率的电子设备结构。
具体实施方式
[0049]
为使本技术的目的、技术方案和优点更加清楚明白，以下结合具体实施例，并参照附图，对本技术进一步详细说明。
[0050]
需要说明的是，除非另外定义，本技术实施例使用的技术术语或者科学术语应当为本技术所属领域内具有一般技能的人士所理解的通常意义。本技术实施例中使用的“第一”、“第二”以及类似的词语并不表示任何顺序、数量或者重要性，而只是用来区分不同的组成部分。“包括”或者“包含”等类似的词语意指出现该词前面的元件或者物件涵盖出现在该词后面列举的元件或者物件及其等同，而不排除其他元件或者物件。“连接”或者“相连”等类似的词语并非限定于物理的或者机械的连接，而是可以包括电性的连接，不管是直接的还是间接的。“上”、“下”、“左”、“右”等仅用于表示相对位置关系，当被描述对象的绝对位置改变后，则该相对位置关系也可能相应地改变。
[0051]
如背景技术部分所述，相关技术中预测存活概率的技术方案，是通过恒定强度来表征个体存活概率的，其只能粗略的度量存活概率，并不具有个体的随机性，导致实际情况的数值和数学模型得到的精确值总是存在很大偏差。
[0052]
因此，本技术提出一种预测存活概率的方法，在现有的预测存活概率的模型中加入随机性，进一步加入不同的跳跃部分，使得预测存活概率模型相比于现有技术而言具有随机性，达到通过模型描述个体存活概率不确定性的技术效果。
[0053]
以下，通过具体的实施例来详细说明本技术实施例的技术方案。
[0054]
参考图1，本技术实施例的预测存活概率的方法，包括以下步骤：
[0055]
步骤s101，利用带有随机强度的cox过程建立第一预测存活概率模型。
[0056]
在一种可能的实现方式中，存活函数是衡量个体死亡风险的重要基准模型，指x岁的个体在t年内存活的概率，通过下式表示：
[0057][0058]
其中，s
x
(t)表示x岁的个体在t年内存活的概率，t
x
表示个体寿命，表示个体寿命t
x
的分布函数，
t
p
x
表示个体年龄为x时，t年后仍活着的概率。
[0059]
本技术实施例从自然死亡率的角度分析存活函数，定义为存活函数对数的负导数，通过下式表示：
[0060][0061]
其中，μ
x
(t)表示死亡力，s
x
(t)表示x岁的个体在t年内存活的概率。
[0062]
通过上述可知，x岁个体在t年内的存活函数转化为下式：
[0063]
[0064]
其中，s
x
(t)表示x岁的个体在t年内存活的概率，
t
p
x
表示个体年龄为x时，t年后仍活着的概率，μ
x
(t)表示死亡力。
[0065]
不考虑疾病情况的死亡力是由当前年龄x和个体出生的自然年共同决定的，若自然年相同，x越大则自然死亡率会增加；保持x一定时，由于医学的发展和生活质量的提高等外在因素，自然死亡率会随着出生自然年的推移而略微降低，在整体水平上拥有更长的平均寿命。因此，在为x岁个体的存活函数建模分析时，需要保持出生年份固定。
[0066]
现有技术中利用“人类死亡率数据库hmd”粗略观测存活函数计算出的自然死亡率，hmd由max planck人口研究所联合加州大学伯克利分校提供，数据库每周更新38个国家和地区的死亡人数。本技术选择1
×
1的表格，即年龄间隔
×
年间隔表，它记录不同的出生自然年、不同年龄的个体的自然死亡情况。个体在每个年龄和每个自然年都被估计了一个死亡概率，即q
x
，x最大取值到110，例如，如果要计算一个在1922年出生，现在x岁的人在t年后仍存活的概率，把每一年的存活概率做乘积。选择的个体年龄为x，对应出生自然年为y，若使用x+1岁的死亡概率时，对应的自然年为y+1，依此类推，通过下式粗略度量死亡力：
[0067]
t
p
x
＝(1-q
x
)(1-q
x+1
)....(1-q
x+t-1
)
[0068]
其中，
t
p
x
表示个体年龄为x时，t年后仍活着的概率，q
x
表示个体在年龄为x时，某个自然年被估计的死亡概率。
[0069]
但粗略度量出的死亡力并不能描述个体死亡风险的差异性与不确定性，为了描述不确定性，本技术引入风险回归模型，简称cox过程。
[0070]
对于具有非负强度函数λ
t
的非齐次泊松过程n满足下式：
[0071][0072]
其中，n
t
表示第一跳跃时间，ns表示初始时间，时间间隔k独立于表示初始时间，时间间隔k独立于表示在某个时间点的波动率参数，τ表示当前时间，s表示考虑的时间范围的值，λu表示时间为u时的非负死亡力强度函数。
[0073]
假设cox过程的第一跳跃时间n
t
表示为τ，则该过程可以看作为不均匀强度的泊松过程，满足下式：
[0074][0075]
其中，τ表示cox过程的第一跳跃时间，λs表示时间为s时的非负死亡力强度函数，e[
·
]表示期望。
[0076]
本技术实施例用到的泊松过程的性质如下所述：“鞅”是一个没有漂移项的随机过程。
[0077]“鞅”满足如下所述的定理：
[0078]
如果n
t
是有固定比率λ的泊松过程，那么过程n
t-λ
t
是一个鞅。
[0079]
如果n
t
是有强度随时间变化的λ
t
非齐次泊松过程，那么其补偿复合泊松过程是一个鞅。
[0080]
本技术实施例将患者个体的存活函数看做死亡发生的泊松过程，自然死亡时间是
泊松过程的第一跳时间，本技术实施例的预测模型以及cox过程中，随机强度允许过度分散或一直波动变化。
[0081]
在一种可能的实现方式中，利用带有随机强度的cox过程建立第一预测存活概率模型，所述第一预测存活概率模型具体为：
[0082][0083]
其中，s
x
(t)表示x岁的个体在t年后的存活概率，t
x
表示x岁的个体的未来寿命时间，表示t＝0，λs表示时间为s时的非负死亡力强度函数。
[0084]
步骤s102，在所述第一预测存活概率模型中加入仿射扩散过程，得到第二预测存活概率模型。
[0085]
在一种可能的实现方式中，需要指定仿射扩散过程作为死亡率强度的模型。
[0086]
对于仿射扩散过程x
t
，有
[0087]
其中，g
t
表示期望随时间t变化，α(t-t)和β(t-t)需要满足“广义riccati常微分方程”，取决于仿射扩散过程的sde系数，通过仿射扩散过程可得到α和β的表达式，用于求解存活函数模型。
[0088]
基于定理：如果u(x,t)在限制条件u(x,t)＝1时满足下述偏微分方程：
[0089][0090]
对u求期望，得到下式：
[0091][0092]
且满足dx
t
＝μ(x
t
,t)dt+σ(x
t
,t)db
t
，其中b
t
表示布朗运动。
[0093]
假设以及所述仿射扩散过程满足以下公式：
[0094]
dx
t
＝μ(x
t
,t)dt+σ(x
t
,t)db
t
[0095]
根据费曼-卡兹公式，如果u(x
t
,t)符合所述偏微分方程式，那么满足下式：
[0096][0097]
同时还可以得到另一个结论：即只有当μ(x
t
,t)和σ2(x
t
,t)满足μ(x
t
,t)＝a+bx
t
且σ2(x
t
,t)＝c+rx
t
时，u(x
t
,t)可被写成e
α(t-t)+β(t-t)x(t)
，则变量满足广义常微分方程，在此种情况下表示为下式：
[0098][0099]
其中，a、b、c、r均为常数。
[0100]
本专利中将μ和σ的这种结构称为“仿射扩散结构”，在存活函数和后续的模型中应用该“仿射扩散结构”来求得riccati常微分方程，重点是显式化表达各个过程中α和β的表
达式，进而进行求解模型。
[0101]
在本技术实施例中，将非负死亡力强度λ
x
(t)作为仿射扩散结构。令t＝t且t＝0，则所述第一预测存活概率模型转换为第二预测存活概率模型，具体为：
[0102][0103]
其中，α(
·
)表示参数，β(
·
)表示参数，s
x
(t)表示x岁的个体在t年后的存活概率，λ
x
(
·
)表示死亡力强度。
[0104]
步骤s103，结合指数跳跃函数，建立关于第二预测存活概率模型的第一参数的费勒函数。
[0105]
在均值回复模型的概念下，个体的差异性会导致只有被认为是更健康的人在老年时的自然死亡率才是符合客观事实的，不能描述个体自然死亡率随任意时间的对应规律。由于个体自然死亡风险随着时间的推移而增加，因此死亡力并不满足均值回复规律，需要使用非均值回复过程来表征个体的自然死亡率，其确定性趋势呈指数增长。
[0106]
在一种可能的实现方式中，所述费勒函数具体为：
[0107][0108]
其中，λ
x
(t)表示所述第一参数，a表示常数，ε表示波动率参数，w
t
表示带有波动率的死亡力强度函数，j(t)表示指数跳跃函数。
[0109]
所述指数跳跃函数通过下式计算：
[0110][0111]
其中，j
t
表示指数跳跃函数，n
t
表示独立于b
t
且带有强度为υ的标准泊松过程，γk(k＝1,2,
…
,n
t
)表示独立同分布随机变量。
[0112]
步骤s104，根据指数分布期望，设置所述第二预测存活概率模型的第二参数和第三参数满足第一限定条件。
[0113]
所述指数分布期望具体为：
[0114][0115]
其中，β(t)表示第三参数，γk(k＝1,2,
…
,n
t
)表示独立同分布随机变量，η表示γk的均值，要求数值上
[0116]
本技术实施例选取具有非均值回复过程的费勒函数作为研究自然死亡强度的基础随机过程，提出在费勒函数中加入不同种类的跳跃部分，根据所述费勒函数将广义riccati常微分方程转化为所述第一限定条件，所述第一限定条件具体为：
[0117]
[0118]
其中，α
′
(t)表示第二参数的微分，β
′
(t)表示第三参数的微分，β(t)表示所述第三参数，l表示跳跃强度，a表示常数，μ表示仿射扩散结构，σ表示仿射扩散结构。
[0119]
步骤s105，根据所述第二参数和第三参数的边界条件，结合第一限定条件，计算得到第二参数和第三参数。
[0120]
在一种可能的实现方式中，所述第二参数和第三参数的边界条件，包括：
[0121]
变量为0时，所述第二参数和所述第三参数均为0。
[0122]
在一种可能的实现方式中，所述第二参数和所述第三参数为：
[0123][0124]
其中，α(t)表示所述第二参数，β(t)表示所述第三参数，l表示跳跃强度，μ表示仿射扩散结构，a、b、c、d均为常数，射扩散结构，a、b、c、d均为常数，
[0125]
步骤s106，结合所述第二参数、所述第三参数、所述费勒函数和所述第二预测存活概率模型计算得到预测存活概率模型。
[0126]
在本步骤中，经上述计算可知第二参数、第三参数以及与第一参数相关的费勒函数，将所述第二参数、第三参数以及与第一参数相关的费勒函数带入到所述第二预测存活概率模型中，计算得到预测存活概率模型。
[0127]
步骤s107，利用所述预测存活概率模型用于对现在x岁的个体在t年后的存活概率进行预测。
[0128]
在本实施例中，利用hmd英国人口数据库的男性数据和女性数据来对存活概率进行预测。
[0129]
预测结果参考图2-图7，图2-图7中的felj_1模型均为本技术的预测存活概率模型，实线为实际存活概率数值曲线，虚线为预测存活概率模型预测出的存活概率数值曲线。
[0130]
图2-图7为1922、1932和1942年，男女性预测存活概率和实际存活概率的对比图。
[0131]
从图中可以看出，预测存活概率的数值曲线和实际存活概率的数值曲线高度吻合，证明本技术的预测存活概率模型预测出的数值十分贴近实际数值，具有十分优异的技术效果。
[0132]
需要说明的是，本技术实施例的方法可以由单个设备执行，例如一台计算机或服务器等。本实施例的方法也可以应用于分布式场景下，由多台设备相互配合来完成。在这种分布式场景的情况下，这多台设备中的一台设备可以只执行本技术实施例的方法中的某一个或多个步骤，这多台设备相互之间会进行交互以完成所述的方法。
[0133]
需要说明的是，上述对本技术的一些实施例进行了描述。其它实施例在所附权利要求书的范围内。在一些情况下，在权利要求书中记载的动作或步骤可以按照不同于上述实施例中的顺序来执行并且仍然可以实现期望的结果。另外，在附图中描绘的过程不一定要求示出的特定顺序或者连续顺序才能实现期望的结果。在某些实施方式中，多任务处理和并行处理也是可以的或者可能是有利的。
[0134]
基于同一发明构思，与上述任意实施例方法相对应的，本技术还提供了一种预测
存活概率的装置。
[0135]
参考图8，所述预测存活概率的装置，包括：
[0136]
建立模块21，被配置为利用带有随机强度的cox过程建立第一预测存活概率模型；
[0137]
仿射扩散模块22，被配置为在所述第一预测存活概率模型中加入仿射扩散过程，得到第二预测存活概率模型；
[0138]
建立模块21，被配置为结合指数跳跃函数，建立关于第二预测存活概率模型的第一参数的费勒函数；
[0139]
设置模块23，被配置为根据指数分布期望，设置所述第二预测存活概率模型的第二参数和第三参数满足第一限定条件；
[0140]
计算模块24，被配置为根据所述第二参数和第三参数的边界条件，结合第一限定条件，计算得到第二参数和第三参数；
[0141]
计算模块24，被配置为结合所述第二参数、所述第三参数、所述费勒函数和所述第二预测存活概率模型计算得到预测存活概率模型；利用所述预测存活概率模型用于对现在x岁的个体在t年后的存活概率进行预测。
[0142]
为了描述的方便，描述以上装置时以功能分为各种模块分别描述。当然，在实施本技术时可以把各模块的功能在同一个或多个软件和/或硬件中实现。
[0143]
上述实施例的装置用于实现前述任一实施例中相应的预测存活概率的方法，并且具有相应的方法实施例的有益效果，在此不再赘述。
[0144]
基于同一发明构思，与上述任意实施例方法相对应的，本技术还提供了一种电子设备，包括存储器、处理器及存储在存储器上并可在处理器上运行的计算机程序，所述处理器执行所述程序时实现上任意一实施例所述的预测存活概率的方法。
[0145]
图9示出了本实施例所提供的一种更为具体的电子设备硬件结构示意图，该设备可以包括：处理器1010、存储器1020、输入/输出接口1030、通信接口1040和总线1050。其中处理器1010、存储器1020、输入/输出接口1030和通信接口1040通过总线1050实现彼此之间在设备内部的通信连接。
[0146]
处理器1010可以采用通用的cpu(central processing unit，中央处理器)、微处理器、应用专用集成电路(application specific integrated circuit，asic)、或者一个或多个集成电路等方式实现，用于执行相关程序，以实现本说明书实施例所提供的技术方案。
[0147]
存储器1020可以采用rom(read only memory，只读存储器)、ram(random access memory，随机存取存储器)、静态存储设备，动态存储设备等形式实现。存储器1020可以存储操作系统和其他应用程序，在通过软件或者固件来实现本说明书实施例所提供的技术方案时，相关的程序代码保存在存储器1020中，并由处理器1010来调用执行。
[0148]
输入/输出接口1030用于连接输入/输出模块，以实现信息输入及输出。输入输出/模块可以作为组件配置在设备中(图中未示出)，也可以外接于设备以提供相应功能。其中输入设备可以包括键盘、鼠标、触摸屏、麦克风、各类传感器等，输出设备可以包括显示器、扬声器、振动器、指示灯等。
[0149]
通信接口1040用于连接通信模块(图中未示出)，以实现本设备与其他设备的通信交互。其中通信模块可以通过有线方式(例如usb、网线等)实现通信，也可以通过无线方式
(例如移动网络、wifi、蓝牙等)实现通信。
[0150]
总线1050包括一通路，在设备的各个组件(例如处理器1010、存储器1020、输入/输出接口1030和通信接口1040)之间传输信息。
[0151]
需要说明的是，尽管上述设备仅示出了处理器1010、存储器1020、输入/输出接口1030、通信接口1040以及总线1050，但是在具体实施过程中，该设备还可以包括实现正常运行所必需的其他组件。此外，本领域的技术人员可以理解的是，上述设备中也可以仅包含实现本说明书实施例方案所必需的组件，而不必包含图中所示的全部组件。
[0152]
上述实施例的电子设备用于实现前述任一实施例中相应的预测存活概率的方法，并且具有相应的方法实施例的有益效果，在此不再赘述。
[0153]
基于同一发明构思，与上述任意实施例方法相对应的，本技术还提供了一种非暂态计算机可读存储介质，所述非暂态计算机可读存储介质存储计算机指令，所述计算机指令用于使所述计算机执行如上任一实施例所述的预测存活概率的方法。
[0154]
本实施例的计算机可读介质包括永久性和非永久性、可移动和非可移动媒体可以由任何方法或技术来实现信息存储。信息可以是计算机可读指令、数据结构、程序的模块或其他数据。计算机的存储介质的例子包括，但不限于相变内存(pram)、静态随机存取存储器(sram)、动态随机存取存储器(dram)、其他类型的随机存取存储器(ram)、只读存储器(rom)、电可擦除可编程只读存储器(eeprom)、快闪记忆体或其他内存技术、只读光盘只读存储器(cd-rom)、数字多功能光盘(dvd)或其他光学存储、磁盒式磁带，磁带磁磁盘存储或其他磁性存储设备或任何其他非传输介质，可用于存储可以被计算设备访问的信息。
[0155]
上述实施例的存储介质存储的计算机指令用于使所述计算机执行如上任一实施例所述的预测存活概率的方法，并且具有相应的方法实施例的有益效果，在此不再赘述。
[0156]
所属领域的普通技术人员应当理解：以上任何实施例的讨论仅为示例性的，并非旨在暗示本技术的范围(包括权利要求)被限于这些例子；在本技术的思路下，以上实施例或者不同实施例中的技术特征之间也可以进行组合，步骤可以以任意顺序实现，并存在如上所述的本技术实施例的不同方面的许多其它变化，为了简明它们没有在细节中提供。
[0157]
另外，为简化说明和讨论，并且为了不会使本技术实施例难以理解，在所提供的附图中可以示出或可以不示出与集成电路(ic)芯片和其它部件的公知的电源/接地连接。此外，可以以框图的形式示出装置，以便避免使本技术实施例难以理解，并且这也考虑了以下事实，即关于这些框图装置的实施方式的细节是高度取决于将要实施本技术实施例的平台的(即，这些细节应当完全处于本领域技术人员的理解范围内)。在阐述了具体细节(例如，电路)以描述本技术的示例性实施例的情况下，对本领域技术人员来说显而易见的是，可以在没有这些具体细节的情况下或者这些具体细节有变化的情况下实施本技术实施例。因此，这些描述应被认为是说明性的而不是限制性的。
[0158]
尽管已经结合了本技术的具体实施例对本技术进行了描述，但是根据前面的描述，这些实施例的很多替换、修改和变型对本领域普通技术人员来说将是显而易见的。例如，其它存储器架构(例如，动态ram(dram))可以使用所讨论的实施例。
[0159]
本技术实施例旨在涵盖落入所附权利要求的宽泛范围之内的所有这样的替换、修改和变型。因此，凡在本技术实施例的精神和原则之内，所做的任何省略、修改、等同替换、改进等，均应包含在本技术的保护范围之内。