一种基于计算机程序的骨折术前计划辅助方法与流程

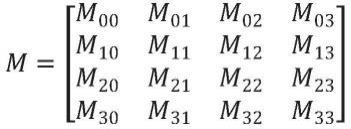
1.本技术涉及外科手术辅助软件领域，尤其涉及一种基于计算机程序的骨折术前计划辅助方法。


背景技术：

2.骨折指的是骨骼因为病理性或创伤性的原因导致的骨完整性破坏或是连续性中断。骨折分为不完全性骨折和完全性骨折，前者是指骨的完整性和连续性部分中断，后者是指骨的完整性和连续性的全部中断。在骨折中，通常会产生骨碎片以及骨断面，相比于原解剖形态，骨碎片为发生了位移或旋转后的骨骼。
3.较严重的骨折通常需要通过手术进行干预治疗。骨折手术的目的是将移位的骨碎片进行复位并进行必要的固定，以恢复骨骼的解剖形态。在骨折手术中，医生需要根据骨碎片的移位情况，通过经验判断骨碎片应当复位的目标位置，并通过创口操作骨碎片进行处理。在实际操作中，骨折发生的部位可能是多个，生成的碎片也可能是多个。尽管目前已经具备了ct、x光等医学影像学技术，但是全面理解骨折线和骨折碎片依然困难。一些小的骨折碎片在术中复位或术后力学功能上起到关键作用，因此其复位往往非常必须，但是在处理大的骨块时，由于受到切口的限制，较小的骨折碎片往往处于不可见的位置。因此，如何选择恰当的切口仍然是个困难。为了选择合适的切口，严格的术前计划就显得非常关键。
4.在现有技术中，存在一些计算机程序手段来辅助外科医生提高手术精度。例如一些虚拟手术计划软件，可以采用病患的医学影像构件虚拟的三维模型，使得医生在系统内对骨骼以及骨折碎片的三维模型进行虚拟的操作，包括观察、移动、旋转等等。外科医生可以在术前对手术进行计划，优化手术步骤和时间。
5.然而，对于骨折手术而言，其目标是将骨折碎片进行复位。尽管现有的手术计划软件能够起到一部分优化的效果，但是如何移动骨折碎片才能与缺损骨骼更好地匹配，以复位固定并恢复其力学性能，对医生的经验和能力有着极高的要求。对于经验较缺乏的医生而言，由于对骨折线理解不足，可能存在匹配精度不高的问题，从而影响手术的精度，无法将匹配精度控制在毫米量级，则会严重影响愈后效果。
6.因此本领域技术人员致力于开发一种基于计算机程序的骨折术前计划辅助方法，来帮助较缺乏经验的医生进行骨折术前计划。


技术实现要素：

7.为实现上述目的，本技术提供了一种基于计算机程序的骨折术前计划辅助方法，具体包括以下步骤：
8.步骤1、获取模型步骤：通过医学影像数据获取骨折部位的三维模型，包括缺损骨骼的三维模型以及骨折碎片的三维模型，其中所述缺损骨骼的三维模型作为第一模型，所述骨折碎片的三维模型作为第二模型；
9.步骤2、粗匹配步骤：求解将所述第二模型进行位置变换到所述第一模型处的粗匹
配变换矩阵；将所述粗匹配变换矩阵应用于所述第二模型，得到第三模型；
10.步骤3、精匹配步骤：给予所述第三模型随机扰动，然后求解将所述第三模型进行位置变换到所述第一模型处的精匹配变换矩阵；将所述精匹配变换矩阵应用于所述第三模型，得到第四模型；
11.步骤4、展示结果步骤：测量所述第四模型与所述第一模型之间的误差，并计算和展示辅助数据。
12.可选地，步骤1中，所述第二模型的数量与所述骨折碎片的数量一致。
13.可选地，步骤2具体包括以下步骤：
14.步骤2.1、由用户在所述第一模型和所述第二模型的对应位置选取一定数量的粗匹配点；
15.步骤2.2、根据所述粗匹配点的位置坐标，计算将所述第二模型进行位置变换到所述第一模型位置处的粗匹配变换矩阵；
16.步骤2.3、将所述粗匹配变换矩阵应用于所述第二模型，得到所述第三模型，并测量所述第三模型与所述第一模型之间的误差。
17.可选地，在步骤2.1中，位于所述第一模型上的所述粗匹配点与位于所述第二模型上对应位置的所述粗匹配点形成粗匹配点组，所述粗匹配点组的数量不小于4。
18.可选地，步骤2.2中，
19.定义位于所述第一模型上的所述粗匹配点p的位置坐标a满足其中x、y、z为三维坐标系中的坐标值，
20.定义位于所述第二模型上的所述粗匹配点p’的位置坐标a’满足其中x’、y’、z’为三维坐标系中的坐标值，
21.将所述粗匹配点p’进行位置变换的第一坐标变换矩阵m为4*4矩阵，其左上角的3*3矩阵为旋转矩阵，右侧4*1矩阵为平移矩阵；
22.通过求解矛盾方程组(m
t
)ma＝(m
t
)a
′
求解所述第一坐标变换矩阵m。
23.可选地，步骤2.2中，采用最小二乘法求解得到粗匹配偏差d最小的所述第一坐标变换矩阵m，即为所述粗匹配变换矩阵，所述粗匹配偏差d满足：
24.d＝∑(m
00
*x+m
01
*y+m
02
*z+m
03-x
′
)2+(m
10
*x+m
11
*y+m
12
*z+m
13-y
′
)2+(m
20
*x+m
21
*y+m
22
*z+m
23-z
′
)2，
25.其中，m
00
、m
01
等为所述第一坐标变换矩阵m中的元素，x、y、z以及x
′
、y
′
、z
′
为坐标值。
26.可选地，步骤3具体包括以下步骤：
27.步骤3.1、在所述第一模型上定义精匹配曲面；
28.步骤3.2、在所述第三模型上随机选取若干精匹配点；
29.步骤3.3、对于每一个所述精匹配点，在所述精匹配曲面上寻找对应的就近匹配点；
30.步骤3.4、根据所述精匹配点以及对应的所述就近匹配点，采用步骤2.2的方式计算将所述第三模型进行位置变换到所述第一模型位置处的第二坐标变换矩阵；
31.步骤3.5、将所述第二坐标变换矩阵应用于所述第三模型，并计算精匹配偏差；
32.步骤3.6、读取预设的精匹配偏差阈值以及预设循环次数并进行条件判定，符合条件则执行下一步，否则回到步骤3.2循环；
33.步骤3.7、将最后一次计算得到的所述第二坐标变换矩阵确定为精匹配变换矩阵。
34.如权利要求7所述的基于计算机程序的骨折术前计划辅助方法，其特征在于，步骤3.2中，所述精匹配点的数量为不少于500个。
35.如权利要求7所述的基于计算机程序的骨折术前计划辅助方法，其特征在于，步骤3.5中，所述精匹配偏差阈值d满足
36.d＝∑((p
a-pb)*nb)237.其中，pa为所述精匹配点的位置向量，pb为所述就近匹配点的位置向量，nb为所述就近匹配点处的法向量。
38.可选地，所述预设循环次数为不少于100次。
39.与现有技术相比，本技术的技术方案至少具备以下技术效果：
40.本方法通过对缺损骨骼以及骨折碎片的三维模型相对位置的识别，通过粗匹配步骤以及精匹配步骤，将骨折碎片精确地与缺损骨骼的骨折断面匹配，最终匹配精度达到毫米级。能够向医生展示匹配以后的三维图像效果，即对解剖形态恢复的效果。同时，还能够向医生提供骨折碎片移动的位移量以及旋转角度等辅助数据，以起到辅助手术计划的技术效果。
41.以下将结合附图对本技术的构思、具体结构及产生的技术效果作进一步说明，以充分地了解本技术的目的、特征和效果。
附图说明
42.图1是本技术一个实施例的流程示意图；
43.图2是本技术一个实施例的三维模型示意图；
44.图3是本技术一个实施例中步骤2的流程示意图；
45.图4是本技术一个实施例中经过粗匹配后的三维模型示意图；
46.图5是本技术一个实施例中步骤3的流程示意图；
47.图6是本技术一个实施例中经过精匹配后的三维模型示意图。
具体实施方式
48.以下参考说明书附图介绍本技术的多个优选实施例，使其技术内容更加清楚和便于理解。本技术可以通过许多不同形式的实施例来得以体现，本技术的保护范围并非仅限于文中提到的实施例。
49.实施例1
50.如图1所示为本实施例的流程图。本实施例提供了一种基于计算机程序的骨折术前计划辅助方法，具体包括以下步骤：
51.步骤1、获取模型步骤，获取缺损骨骼以及骨折碎片的三维模型。
52.在本实施例中，步骤1具体包括以下步骤：
53.步骤1.1、将病患骨折部位的ct影像数据导入到模型重构系统中；
54.步骤1.2、采用三维重构算法，基于二维影像数据生成缺损骨骼以及骨折碎片的三维模型。
55.如图2所示，本实施例中为了讨论和演示更方便，采用一个脚掌部位的骨骼进行三维重构后生成第一模型用于代替缺损骨骼；将第一模型进行一定程度的移位、旋转以后生成第二模型用于代替骨折碎片。采用本实施例的方法能够将第二模型与第一模型精确地匹配，则说明将本方法应用于骨折手术计划中，能够将骨折碎片与缺损骨骼精确地匹配。在实际临床中，可能存在多个骨折碎片，则需要生成多个第二模型，第二模型的数量与骨折碎片的数量一致，并依次将多个第二模型与第一模型进行匹配。
56.步骤2、粗匹配步骤：求解将所述第二模型进行位置变换到所述第一模型处的粗匹配变换矩阵；将所述粗匹配变换矩阵应用于所述第二模型，得到第三模型。
57.在本实施例中，如图3所示，步骤2具体包括以下步骤：
58.步骤2.1、用户在第一模型和第二模型上选取一定数量的粗匹配点。
59.在本步骤中，用户(通常是医生)根据个人经验，以复原解剖学状态为目标，选取第一模型、第二模型上对应位置的粗匹配点组p。例如在本实施例中，在第一模型和第二模型上各选取位于脚掌上的对应位置的点，作为粗匹配点组p。每一个粗匹配点组由两个粗匹配点(位于第一模型上的p、位于第二模型上的p’)组成。通常粗匹配点的数量不少于4组。
60.如图2所示，在本实施例中优选地，用户选取了脚趾部位附近的5组粗匹配点组(p1，p1’
)、(p2，p2’
)
……
依次类推。
61.步骤2.2、根据对应的粗匹配点的位置坐标，计算将第二模型进行位置变换到第一模型位置处的粗匹配矩阵。
62.在本实施例中，对于每一个粗匹配点组p而言，定义：
63.粗匹配点p的位置坐标为
64.粗匹配点p’的位置坐标为
65.将粗匹配点p’进行位置变换的坐标变换矩阵m为4*4矩阵，且满足
[0066][0067]
其中，左上角的3*3矩阵为旋转矩阵，右侧4*1矩阵为平移矩阵；
[0068]
对于每一组粗匹配点组p中的p和p’，将其位置坐标以及坐标变换矩阵m代入矛盾方程组，并在等号两边均左乘坐标变换矩阵的转置矩阵m
t
，则得到如下方程组：
[0069]
(m
t
)ma＝(m
t
)a
′
[0070]
采用最小二乘法求解该矛盾方程组，得到粗匹配偏差d为最小值时的坐标变换矩阵m，即为从第二模型到第一模型的粗匹配变换矩阵。
[0071]
粗匹配偏差定义为d＝∑(m
00
*x+m
01
*y+m
02
*z+m
03-x
′
)2+(m
10
*x+m
11
*y+m
12
*z+m
13-y
′
)2+(m
20
*x+m
21
*y+m
22
*z+m
23-z
′
)2，
[0072]
其中，m
00
、m
01
等为所述第一坐标变换矩阵m中的元素，x、y、z以及x’、y’、z’为坐标值。
[0073]
步骤2.3、将粗匹配矩阵应用于第二模型，第二模型进行坐标变换以后生成第三模型。
[0074]
将步骤2.2中求解得到的粗匹配矩阵对第二模型进行位置变换，得到与第一模型较接近的第三模型。对于理想的骨折手术而言，用户总是希望每一个粗匹配点组p中包含的粗匹配点p、p’经过模型的位置和角度变换后严格重合在一起。但在实际场景中，骨折部位的骨断面呈现复杂的不规则曲面，另外由于用户个人经验或观察、操作等方面的限制，无法对实际骨断面的每一个细节都观察和理解透彻，因此实际并不能选取到骨断面上位置严格对应的点位。因此，对第二模型进行位置变换或旋转变换后，并不能保证每一个粗匹配点组p最终均能够严格地重合在一起，只能在各组粗匹配点之间找到一个相对误差最优的匹配位置。
[0075]
在本实施例中优选地，如图4所示为经过粗匹配步骤后的第一模型以及第三模型，图中较深颜色的部分展示了第一模型与第三模型未能重合的部分。经过工具测量，在粗匹配步骤完成以后，第三模型与第一模型之间最大的误差为9.8mm。
[0076]
步骤3、精匹配步骤；
[0077]
经过粗匹配步骤以后，骨折碎片相对于缺损骨骼而言，进行了一定程度的复位，但由于个人经验、观察角度、选取精度等等的限制，匹配的精度较低。因此本方法提供了精匹配步骤，精匹配步骤的总体思路为，给予第三模型一定程度的随机扰动：在第三模型上随机选取若干点，并找到第一模型上对应的点，并进行坐标变换，然后计算偏差，当偏差达到预设的精度要求后，停止扰动。
[0078]
如图5所示，在本实施例中优选地，步骤3具体包括以下步骤：
[0079]
步骤3.1、在第一模型上定义精匹配曲面s。
[0080]
在本实施例中，由于第一模型与第三模型的尺寸相同，因此可以定义整个脚掌模型的外表面作为精匹配曲面s。在其他优选的实施例中，精匹配曲面s即为缺损骨骼与骨折碎片分离处的骨断面。骨折手术的目的，即为将骨折碎片通过位置变换和旋转变换贴合至骨断面上，以实现解剖学状态的复原。
[0081]
步骤3.2、在第三模型上随机选取若干精匹配点p
lk
，形成精匹配点集p
lk
。
[0082]
在本实施例中优选地，选取了500个精匹配点p
lk
。在其他的实施例中，一般选取不少于500个精匹配点p
lk
。
[0083]
步骤3.3、对于精匹配点集p
lk
中的每一个精匹配点p
lk
，在精匹配曲面s上寻找对应的就近匹配点p
rk
，以形成就近匹配点集p
rk
。
[0084]
具体的规则为，在精匹配曲面s上，与某个精匹配点p
lk
距离最近的点，即为其所对应的就近匹配点p
rk
。
[0085]
步骤3.4、对于精匹配点集p
lk
以及对应的就近匹配点集p
rk
，采用步骤2.2的步骤求解坐标变换矩阵m。
[0086]
步骤3.5、采用坐标变换矩阵m对精匹配点集p
lk
进行位置变换，并计算位置变换后
的精匹配点集p
lk
与就近匹配点集p
rk
之间的精匹配偏差d，具体计算公式为：
[0087]
d＝∑((p
a-pb)*nb)2[0088]
其中，pa为精匹配点p
lk
的位置向量，pb为就近匹配点p
rk
的位置向量，nb为就近匹配点p
rk
处的法向量。
[0089]
步骤3.6、读取预设的偏差阈值以及预设循环次数，并进行判断：
[0090]
当精匹配偏差d大于偏差阈值，且循环次数小于预设循环次数时，循环执行步骤3.2～步骤3.6；
[0091]
当精匹配偏差d小于等于偏差阈值，或循环次数等于预设循环次数时，执行下一步。
[0092]
步骤3.7、将最后一次计算得到的坐标变换矩阵m作为精匹配变换矩阵，将精匹配变换矩阵应用于第三模型，得到第四模型。
[0093]
在本实施例中优选地，偏差阈值设置为2mm，预设循环次数设置为100次。
[0094]
步骤4、展示匹配结果以及辅助信息。
[0095]
基于求得的精匹配变换矩阵计算辅助数据，在界面上显示辅助数据。本实施例中优选地，根据变换矩阵m，计算得到分别绕x轴、y轴、z轴旋转的角度，以及平移的距离。本实施例中经过精匹配的模型示意图如图6所示，尽管同样采用颜色较深的部分用于展示第一模型和第四模型未能重合的部分，但在图6中已经几乎无法用肉眼发现未重合部分(看不到深色部分)。通过工具测量，第一模型、第四模型之间的最大误差约为1.96mm。由此说明，经过粗匹配、精匹配后，缺损骨骼与骨折碎片之间的复位误差已经达到毫米量级的精度。用户不仅可以通过软件界面观察骨折碎片复位以后的形态，同时还能参考软件给出的平移距离以及旋转角度，为手术计划起到辅助作用。
[0096]
以上详细描述了本技术的较佳具体实施例。应当理解，本领域的普通技术无需创造性劳动就可以根据本技术的构思作出诸多修改和变化。因此，凡本技术领域中技术人员依本技术的构思在现有技术的基础上通过逻辑分析、推理或者有限的实验可以得到的技术方案，皆应在由权利要求书所确定的保护范围内。