一种考虑针尖回弹的柔性针建模方法

1.本发明涉及一种考虑针尖回弹的柔性针建模方法


背景技术：

2.微创介入是近年来迅速发展起来的一门崭新的医疗技术，在临床手术中广泛应用，并成为热点学科。它有很多优点像创伤小、快疗效、安全性高、定位准确，成为当代医疗界的焦点。靶向穿刺技术是微创介入中应用最为广泛的医疗手段，是癌症等重大疾病的重要诊断和治疗手段，其主要的应用方面在人体软组织器官中，如前列腺、乳腺、肝脏、肺脏和大脑等的活体组织取样检查、短距离放射性治疗和冷热消融等手术中。由于人体组织在穿刺过程中出现的漂移和变形，以及在手动穿刺过程中，医生操作手法的不确定性，传统的刚性针穿刺技术是不够优秀的，很难实现精确定位控制，更不可能绕过人体各种组织，实现人体局部的靶向穿刺。采用“柔性针”来代替传统的“刚性针”是一个开创性的思维，克服了刚性针存在的上述弊端。
3.本文采用的穿刺针是镍钛合金材质，具有超级的柔性。柔性针的针尖一般带有斜面，称作斜尖柔性针，利用穿刺时针尖斜面与组织之间的侧向作用力使针轴产生弯曲变形，从而修正偏差和绕过障碍，实现精确的靶向穿刺。因此有必要深入研究柔性针在穿刺过程中，柔性针与组织间的相互作用力，建立各个力的数学模型；并根据建立的数学模型，得到作用于针轴与针尖的受力模型，在受力模型基础上，利用弹性力学理论建立柔性针回弹位移模型，在前两个模型基础上建立柔性针穿刺过程中的弯曲模型。


技术实现要素：

4.本发明的目的是提供一种考虑针尖回弹的柔性针建模方法，根据建立的力学模型，得到作用于针轴与针尖的受力模型，在受力模型基础上，利用弹性力学理论建立柔性针回弹位移模型，在前两个模型基础上建立柔性针穿刺过程中的弯曲模型。
5.为达到上述目的，本发明的技术方案中，一种考虑针尖回弹的柔性针建模方法，其特征在于，在柔性针穿刺过程中，将针与组织之间的作用力包括为：柔性针的末端进给力f
p
、夹紧力fc、夹紧摩擦力f
cf
、抵抗力fr、抵抗摩擦力f
rf
、以及切割反作用力f
t
作用，他们共同耦合作用产生了柔性针在组织中的弯曲。φ(x)为柔性针弯曲时针轴与水平方向的夹角，选取镍钛合金材质的柔性针，该发明方法包括以下步骤：
6.1)建立夹紧力及夹紧摩擦力模型、切割反力模型、组织抵抗力及抵抗摩擦力模型，根据建立的力学模型，得到作用于针轴与针尖的受力模型和柔性针回弹位移建模；
7.2)根据建立的力学模型，得到柔性针单弯曲与双弯曲模型。
8.优选地，步骤1)中建立夹紧力及夹紧摩擦力、切割反力、组织抵抗力及抵抗摩擦力模型，根据建立的力学模型，得到作用于针轴与针尖的受力模型和柔性针回弹位移的建模过程如下：
9.fc为针在穿刺过程中组织被压缩进而会对针施加的一个夹紧力，单位摩擦力f
cf
表
示的是组织作用在单位长度针段上的摩擦力，其与夹紧摩擦力f
cf
的关系为：
[0010][0011]
式中：l
input
表示组织内部针段的长度；
[0012]
由式(1)可知，只要求得单位摩擦力f
cf
便可确定穿刺任何长度下的夹紧摩擦力f
cf
，通过力传感器得到f
cf
,根据所得的夹紧摩擦力可以求出单位摩擦力：
[0013][0014]
夹紧力可以表示为：
[0015][0016]
切割反力作用于斜面上，方向与斜面垂直。本文设定针尖沿直线对组织进行切割且将切割反力视为针尖斜面上的三角分布载荷均布载荷χ可以表示为：
[0017]
χ＝k
t
η
ꢀꢀꢀ
(4)
[0018]
式中：k
t
为组织刚度系数；η为载荷作用方向；
[0019]
因此，作用于针尖的切割反力为：
[0020][0021]
式中：b针尖斜面长度，可以用针轴直径d和针尖斜角a表示：
[0022][0023]
根据受力平衡，可以建立柔性针穿刺组织的水平方向受力表达式为：
[0024]fp-f
c,x-f
cf,x-f
t,x
+f
r,x-f
rf,x
＝0
ꢀꢀꢀ
(7)
[0025]
其中组织抵抗力分力f
r，x
、抵抗摩擦力分力f
rf，x
与抵抗力的关系为：
[0026]fr,x
＝f
r sinφ(x)
ꢀꢀꢀ
(8)
[0027]frf,x
＝μf
r cosφ(x)
ꢀꢀꢀ
(9)
[0028]
式中：柔性针弯曲时针轴与水平方向的夹角φ(x)为：
[0029][0030]
式中：v
pol
为柔性针穿刺软组织的弯曲曲线；
[0031]
夹紧力的分力f
c，x
可以根据公式(3)中所建立的夹紧力模型得到，夹紧力水平分力表达式为：
[0032][0033]
根据公式(1)建立的夹紧摩擦力模型可以得到夹紧摩擦力的分力f
cf，x
表达式为：
[0034]fcf,x
＝f
cf
l
input cosφ(x)
ꢀꢀꢀ
(12)
[0035]
切割反力分力f
t，x
可以根据公式(5)中所建立的切割反力模型得到，表达式为：
[0036][0037]
抵抗摩擦力表达式：
[0038]fr,f
＝μfrꢀꢀꢀ
(14)
[0039]
根据针-组织摩擦力实验测得的摩擦系数μ；
[0040]
在公式(5)中得到了切割反力f
t
模型，由于切割反力垂直作用于针尖斜面，柔性针针尖角α已知，可以得到穿刺过程中不同时刻切割反力f
t
的分力f
t，y
；
[0041]ft,y
(x)＝f
t cosα
ꢀꢀꢀ
(15)
[0042]
根据公式(3)夹紧力模型以及公式(5)建立的切割反力模型，建立力学平衡方程式：
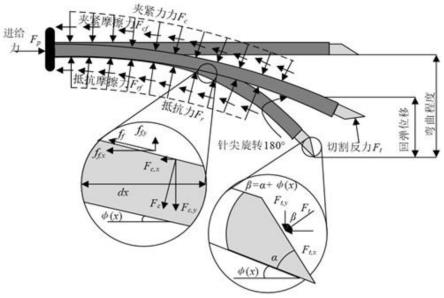
[0043][0044]
式中：f
p
为柔性针针尾处电机提供的进给力，可以有力传感器测得。根据针-组织摩擦力实验测得的摩擦系数μ；
[0045]
对针穿刺软组织过程中的回弹位移的建模过程如下：
[0046]
柔性针往往需要通过针尖的旋转来避开障碍，但穿刺过程中第二段弯曲会对第一段弯曲产生干涉，导致第一段弯曲路径发生非线性位移，即柔性针的回弹现象。将柔性针穿刺软组织过程中针段nmq定义为柔性针的回弹针段，利用该针段建立柔性针回弹位移模型；
[0047]
为便于模型建立及求解，将针段nmq回弹方向接触的组织视为一个长方形，并以n点为原点建立对应的坐标系，长方形宽为2r，其长为：
[0048][0049]
式中：a为针尖旋转后的进针长度；φ(xn)为n点处针轴与水平方向的夹角；
[0050]
根据步骤1)回弹受力分析，可以得到夹紧力及抵抗力的均布载荷p的表达式为：
[0051][0052]
垂直作用于针轴的切割反力分力f
t,y
可表示为：
[0053]ft,y
＝f
t cos a
ꢀꢀꢀ
(19)
[0054]
式中：α为针尖角度；
[0055]
首先分析夹紧力与抵抗力组成的均布载荷p，对矩形区域amqb中原针点m处所产生的回弹位移l
amqb
。把单元上的微元载荷当做集中载荷，根据弹性力学理论，计算出该微元载荷在点m处的位移为：
[0056][0057]
式中：ω为修正系数；e为组织的杨氏模量；μ为组织的泊松比；
[0058]
用d表示矩形区域amqb，则矩形区域amqb在点m处所产生的位移为：
[0059][0060]
将积分区域d分解为两个区域，分别记为d1和d2。那么则有：
[0061][0062]
d1和d2范围用极坐标表示为：
[0063][0064]
式中:
[0065]
将式(23)代入(22)中，有：
[0066][0067]
将式(24)代入式(25)，并令可得到：
[0068][0069]
将式(26)代入式(21)中，可以得到矩形区域amqb中点m处所产生的回弹位移表达式为：
[0070][0071]
在整个回弹针段上中点m(原针点)位移为：
[0072][0073]
设点h(x,0)是x轴任意一点，整个针段被点h分为两个部分，分别记为ⅰ、ⅱ；
[0074]
求解不同的矩形局域上某一点回弹位移，只需要将公式(27)中的m做对应的变换，便可得到对应的位移公式；
[0075]
对于区域ⅰ：
[0076]
对于区域ⅱ：
[0077]
令
[0078][0079]
则在均布载荷作用下，区域中各点所产生的回弹位移l(x)可表示为：
[0080][0081]
在穿刺过程中，切割反力的分力f
t,y
只作用于针尖，在研究f
t,y
作用下产生的回弹，需要将其作为一个集中载荷进行计算；
[0082]
在集中载荷作用下，针段回弹位移s(x)为：
[0083][0084]
结合式(28)，得到柔性针针体回弹位移g(x)表达式为：
[0085]
g(x)＝l(x)+s(x)
ꢀꢀꢀ
(34)
[0086]
由于式(33)求得的是垂直于针轴方向的回弹位移，为便于后续的双弯曲建模，我们将其转变为垂直于水平方向的位移g，可表示为：
[0087]
g(x)＝g(x)sinφ(x)
ꢀꢀꢀ
(35)
[0088]
式中：φ(x)为针轴轴线与水平方向夹角。
[0089]
优选地，步骤2)中，在力学模型基础上，对针穿刺软组织过程中的单弯曲变形以及双弯曲变形的建模过程如下：
[0090]
对针穿刺软组织过程中的单弯曲的建模过程如下：
[0091]
采用瑞利-里兹法完成柔性针的单弯曲变形建模工作，系统能量π可以表示为：
[0092]
π＝u+w
ꢀꢀꢀ
(36)
[0093]
式中：u表示系统中的势能；w为外力对系统所做的功；
[0094]
柔性针的弯曲能ub可表示为：
[0095][0096]
式中：e为柔性针材料的杨氏模量；i为转动惯量；l
input
为针的长度；ρ为针的弯曲半径可以表示为：
[0097][0098]
组织具有压缩势能us为：
[0099][0100]
式中：k
t
为组织弹簧刚度；y(x)为柔性针弯曲函数；
[0101]
根据步骤1)的力学建模推导出轴向力f
x
及侧向力fy，进而得到做功表达式：
[0102][0103]
式中：l为针穿刺距离；
[0104]
针尾进给力作功
[0105]winput
＝f
p
l
input
ꢀꢀꢀ
(41)
[0106]
系统能量π可以表示为：
[0107]
π＝ub+us+w
input-w
m-wnꢀꢀꢀ
(42)
[0108]
在保证准确性的基础上，为便于后期系数的求解采用三次多项式作为柔性针位移函数，表达式为：
[0109]
y(x)＝a+bx+cx2+dx3ꢀꢀꢀ
(43)
[0110]
穿刺过程和中的边界条件为：
[0111][0112]
最小势能驻值条件为：
[0113][0114]
通过分步求解得到系数a、b、c、d的值；
[0115]
对针穿刺软组织过程中的双弯曲的建模过程如下：
[0116]
柔性针在穿刺软组织过程中，斜尖方向的改变会导致穿刺方向发生变化，进而形成针的双弯曲轨迹；
[0117]
柔性针双弯曲穿刺过程分为三步：首先，柔性针穿刺形成单弯曲路径；其次，针尖转动180
°
；最后，柔性针继续穿刺，形成双弯曲路径。路径起点为原点o1，终点为o2(xb,yb)。为了便于分析，以单弯曲轨迹终点o2为原点，该点处切线为ξ轴建立新的坐标系ξo2η，ξ轴与水平线夹角为φ(xb)。在不考虑回弹的影响下，变换过程如下；
[0118]
坐标系变换：进行坐标系平移，使得两坐标系原点重合，再对坐标系旋转使得对应坐标轴重合，参考坐标系转换原则，两个坐标系中点的齐次变换矩阵为：
[0119][0120]
式中：(x,y)为单弯曲轨迹中的点；
[0121]
对称变换：将单弯曲曲线终点位置的切线确定为坐标变换的对称轴，并进行坐标变换。设切线方程为ax+by+c＝0，则对应变换后横、纵标为：
[0122][0123]
在柔性针的第一段弯曲中的针尖旋转点为o2(xb,yb),则在不考虑回弹的前提下，
新一轮的穿刺轨迹y(x)'可视为第一段穿刺轨迹y(x)绕点o2(xb,yb)旋转180
°
的结果，因此能得到如下关系:
[0124]
y(x)'＝2y
b-y(2x
b-x),(x＞xb)
ꢀꢀꢀ
(48)
[0125]
根据建立的单弯曲理论轨迹模型的曲线函数，结合上述坐标变换可得到无回弹下的双弯曲轨迹；
[0126]
联立公式(35)与公式(48)便可得到受回弹影响下的双弯曲曲线。
[0127]
本发明的优点在于：
[0128]
1.本发明方法在考虑柔性针穿刺软组织过程中收到的夹紧摩擦力、组织抵抗力、支撑摩擦力和组织抵抗摩擦力等相关因素的影响的前提下，在力学建模的基础上，利用瑞利-里兹法对针穿刺软组织过程中的弯曲变形进行理论建模，求得的位移函数可以预测针穿刺不同软组织的轨迹。
[0129]
2.本发明方法在虑针尖回弹的柔性针建模过程中，深入分析柔性针与组织间的相互作用力，建立各个力的数学模型；并根据建立的数学模型，得到作用于针轴与针尖的受力模型，在受力模型基础上，利用弹性力学理论建立柔性针回弹位移模型，在前两个模型基础上建立柔性针穿刺过程中的弯曲模型。
附图说明
[0130]
附图1，本发明的柔性针穿刺软组织受力示意图；
[0131]
附图2，柔性针回弹区域分析示意图；
[0132]
附图3，回弹区域组织坐标示意图；
[0133]
附图4，均布载荷作用下任意点位移分析示意图；
[0134]
附图5，集中力作用下位移分析示意图。
[0135]
附图1中，柔性针的末端进给力f
p
、夹紧力fc、夹紧摩擦力f
cf
、抵抗力fr、抵抗摩擦力f
rf
、以及切割反作用力f
t
作用，他们共同耦合作用产生了柔性针在组织中的弯曲。φ(x)为柔性针弯曲时针轴与水平方向的夹角。
具体实施方式
[0136]
本发明提出的一种考虑针尖回弹的柔性针建模方法，结合附图1、2、3、4、5所示，一种考虑针尖回弹的柔性针建模方法，其特征在于，在柔性针穿刺过程中，将针与组织之间的作用力包括为：柔性针的末端进给力f
p
、夹紧力fc、夹紧摩擦力f
cf
、抵抗力fr、抵抗摩擦力f
rf
、以及切割反作用力f
t
作用，他们共同耦合作用产生了柔性针在组织中的弯曲，φ(x)为柔性针弯曲时针轴与水平方向的夹角，选取镍钛合金材质的柔性针，该发明方法包括以下步骤：
[0137]
1)建立夹紧力及夹紧摩擦力模型、切割反力模型、组织抵抗力及抵抗摩擦力模型，根据建立的力学模型，得到作用于针轴与针尖的受力模型和柔性针回弹位移建模；
[0138]
2)根据建立的力学模型，得到柔性针单弯曲与双弯曲模型。
[0139]
优选地，步骤1)建立夹紧力及夹紧摩擦力模型、切割反力模型、组织抵抗力及抵抗摩擦力模型，根据建立的力学模型，得到作用于针轴与针尖的受力模型和柔性针回弹位移建模的建模过程如下：
[0140]
夹紧力及夹紧摩擦力建模：
[0141]
fc为针在穿刺过程中组织被压缩进而会对针施加的一个夹紧力，当柔性针直径、针尖角度等参数固定后，针的穿刺轨迹无论是直线还是曲线，只要刺入组织的长度相同，那么针在组织内部占据的空间是相同的，进而组织作用在针轴上的夹紧力fc也是相同的，与此同时由夹紧力fc产生的摩擦力f
cf
也应该一致。单位摩擦力f
cf
表示的是组织作用在单位长度针段上的摩擦力，其与夹紧摩擦力f
cf
的关系为：
[0142][0143]
式中：l
input
表示组织内部针段的长度；
[0144]
由式(1)可知，只要求得单位摩擦力f
cf
便可确定穿刺任何长度下的夹紧摩擦力f
cf
。针的尾部置有力传感器，用于测量针的水平方向受力情况。在退针过程中，只有柔性针针轴在组织内部，且针体并未发生弯曲。此时可认为柔性针只受到组织给予的夹紧力与夹紧摩擦力。由于夹紧力与针轴垂直，夹紧摩擦力方向与针轴线平行，所以，力传感器测得的数据仅为夹紧摩擦力。根据所得的夹紧摩擦力可以求出单位摩擦力：
[0145][0146]
根据所得的摩擦系数，夹紧力可以表示为：
[0147][0148]
切割反力建模：
[0149]
柔性针穿刺组织的过程当中，针尖会对组织进行切割破坏，在此过程中，组织会给予针尖处一个反作用力，许多文献把这个力称为切割力，但严格意义上讲，以柔性针为受力研究对象，组织给予针尖上的反作用力应被称为切割反力。当柔性针的直径和针尖斜角确定后，针尖部分与组织的接触面积为一个定值，在穿刺速恒定以及组织刚度不变情况下，组织给予针尖处的切割反力也是确定的，即针尖处的切割反力为一个常数。由于器官内的液体会润滑针头，因此，切割反力产生的微小摩擦可以忽略；
[0150]
切割反力作用于斜面上，方向与斜面垂直。本文设定针尖沿直线对组织进行切割且将切割反力视为针尖斜面上的三角分布载荷均布载荷χ可以表示为：
[0151]
χ＝k
t
η
ꢀꢀꢀ
(4)
[0152]
式中：k
t
为组织刚度系数；η为载荷作用方向；
[0153]
因此，作用于针尖的切割反力为：
[0154][0155]
式中：b针尖斜面长度，可以用针轴直径d和针尖斜角a表示：
[0156][0157]
柔性针在穿刺组织时，因斜尖处受力不平衡，导致针产生弯曲。组织抵抗力fr是组织为抵抗针弯曲变形而施加在针上的力，方向垂直于针轴。由于组织抵抗力是随着针弯曲程度变化而变化的，因此很难通过实验的方式直接得到，需要将抵抗力从复杂的受力系统
中分离出来，从而完成组织抵抗力及组织抵抗摩擦力的力学建模；
[0158]
由于针是低速穿刺且速度不变，所以在针进给方向上的受力可视为处于平衡状态。针在水平方向上所受到的作用力包括：末端进给力f
p
、夹紧力水平分力f
c,x
、夹紧摩擦力水平分力f
cf,x
、针尖处切割反力水平分力f
t,x
、组织抵抗力水平分力f
r,x
以及抵抗摩擦力水平分力f
rf,x
。根据受力平衡，可以建立柔性针穿刺组织的水平方向受力表达式为：
[0159]fp-f
c,x-f
cf,x-f
t,x
+f
r,x-f
rf,x
＝0
ꢀꢀꢀ
(7)
[0160]
组织抵抗力及抵抗摩擦力建模：
[0161]
其中组织抵抗力分力f
r，x
、抵抗摩擦力分力f
rf，x
与抵抗力的关系为：
[0162]fr,x
＝f
r sinφ(x)
ꢀꢀꢀ
(8)
[0163]frf,x
＝μf
r cosφ(x)
ꢀꢀꢀ
(9)
[0164]
式中：柔性针弯曲时针轴与水平方向的夹角φ(x)为：
[0165][0166]
式中：v
pol
为柔性针穿刺软组织的弯曲曲线；
[0167]
夹紧力水平分力表达式为：
[0168][0169]
根据公式(1)建立的夹紧摩擦力模型可以得到夹紧摩擦力的分力f
cf，x
表达式为：
[0170]fcf,x
＝f
cf
l
input cosφ(x)
ꢀꢀꢀ
(12)
[0171]
切割反力分力f
t，x
可以根据公式(5)中所建立的切割反力模型得到，表达式为：
[0172][0173]
抵抗摩擦力表达式：
[0174]fr，f
＝μfrꢀꢀꢀꢀ
(14)
[0175]
根据针-组织摩擦力实验测得的摩擦系数μ；
[0176]
在公式(5)中得到了切割反力f
t
模型，由于切割反力垂直作用于针尖斜面，柔性针针尖角α已知，可以得到穿刺过程中不同时刻切割反力f
t
的分力f
t，y
；
[0177]ft,y
(x)＝f
t cosα
ꢀꢀꢀ
(15)
[0178]
根据公式(3)夹紧力模型以及公式(5)建立的切割反力模型，建立力学平衡方程式：
[0179][0180]
式中：f
p
为柔性针针尾处电机提供的进给力，可以有力传感器测得。根据针-组织摩擦力实验测得的摩擦系数μ；
[0181]
对针穿刺软组织过程中的回弹位移的建模过程如下：
[0182]
柔性针往往需要通过针尖的旋转来避开障碍，但穿刺过程中第二段弯曲会对第一段弯曲产生干涉，导致第一段弯曲路径发生非线性位移，即柔性针的回弹现象。在所建立的回弹受力模型基础上，对柔性针的回弹进行研究，建立回弹位移模型；
[0183]
在建模之前，需要确定柔性针的回弹针段。图2为柔性针回弹区域示意图，柔性针穿刺组织产生第一次弯曲路径记为y1，针轴旋转180
°
继续穿刺δl后形成弯曲路径y2。弯曲路径y2的针尖记为点q(xq,yq)，y1的针尖点对应在弯曲路径y2中的m点，称m点为第一段弯曲的原针尖点。在弯曲路径y2中取一点n，其横坐标为|x
m-δl|，坐标记为n(xn,yn)。n点、m点与q点便形成了一段以点m为中心的针段nmq，我们将针段nmq定义为柔性针的回弹针段，利用该针段建立柔性针回弹位移模型；
[0184]
为便于模型建立及求解，将针段nmq回弹方向接触的组织视为一个长方形，并以n点为原点建立对应的坐标系，如图3所示，长方形宽为2r，其长为：
[0185][0186]
式中：a为针尖旋转后的进针长度；φ(xn)为n点处针轴与水平方向的夹角；
[0187]
根据柔性针回弹受力分析，图3中2a
×
2r区域主要受切割反力、夹紧力及组织抵抗力作用，本专利将作用于针轴的夹紧力与抵抗力视为均布载荷，作用于针尖的切割反力视为集中载荷进行计算；
[0188]
根据回弹受力分析，可以得到夹紧力及抵抗力的均布载荷p的表达式为：
[0189][0190]
垂直作用于针轴的切割反力分力f
t,y
可表示为：
[0191]ft,y
＝f
t
cosa(19)
[0192]
式中：α为针尖角度；
[0193]
首先分析夹紧力与抵抗力组成的均布载荷p，对图3amqb区域中原针点m处所产生的位移l
amqb
。在amqb区域上选取一点(x,y)，并以该点为中心作一个长、宽分别dx、dy的矩形单元，则该矩形单元上的载荷大小可表示为pdxdy。由微元分析法可知，在足够小的区域内，可以把单元上的微元载荷当做集中载荷来处理，根据弹性力学理论，计算出该微元载荷在点m处的位移为：
[0194][0195]
式中：ω为修正系数；e为组织的杨氏模量；μ为组织的泊松比；
[0196]
用d表示矩形区域amqb，则矩形区域amqb在点m处所产生的位移为：
[0197][0198]
式中的积分在直角坐标系下将很难计算，所以，引入极坐标进行求解。为了计算简便，极坐标系原点设置在m处，极轴与x轴重合。将积分区域d分解为两个区域，分别记为d1和d2，如图3所示。那么则有：
[0199][0200]
d1和d2范围用极坐标表示为：
[0201][0202]
式中:
[0203]
将式(23)代入(22)中，有：
[0204][0205]
将式(24)代入式(25)，并令可得到：
[0206][0207]
将式(26)代入式(21)中，可以得到矩形区域amqb中点m处所产生的回弹位移表达式为：
[0208][0209]
由于回弹针段视为一个矩形，因此整个2a
×
2r区域是对称的，故而整个区域上，均布载荷使得点m产生的沉降位移l(a)应该是l
amqb
的4倍。在整个回弹针段上中点m(原针点)位移为：
[0210][0211]
得到原针点m的回弹位移模型后，接下来分析图3中针段nmq上任意一点的回弹位移，设点h(x,0)是x轴任意一点，整个针段被点h分为两个部分，分别记为ⅰ、ⅱ，如图4所示；
[0212]
求解不同的矩形局域上某一点回弹位移，只需要将公式(27)中的m做对应的变换，便可得到对应的位移公式；
[0213]
对于区域ⅰ：
[0214]
对于区域ⅱ：
[0215]
令
[0216][0217]
则在均布载荷作用下，区域中各点所产生的回弹位移l(x)可表示为：
[0218][0219]
在穿刺过程中，与组织夹紧力及抵抗力不同的是，切割反力的分力,f
t,y
只作用于针尖，因此，在研究f
t,y
作用下产生的回弹，需要将其作为一个集中载荷进行计算，切割反力分力作用示意图如图5所示；
[0220]
在2a
×
2r的组织区域，切割反力分力作用下点的回弹位移函数为s(x)。在弹性力学中，受垂直于平面的集中力作用下任意一点位移可表示为：
[0221][0222]
而当x＝2a时，在该点做一个边长为2r的小正方形，将集中载荷视为小正方形上的均布载荷，则只需要将公式(27)中p替换为f/4r2，此时，m＝1，可以得到该点的回弹位移为：
[0223][0224]
因此，在集中载荷作用下，针段回弹位移s(x)为：
[0225][0226]
结合式(28)，得到柔性针针体回弹位移g(x)表达式为：
[0227]
g(x)＝l(x)+s(x)
ꢀꢀꢀ
(36)
[0228]
由于式(35)求得的是垂直于针轴方向的回弹位移，为便于后续的双弯曲建模，我们将其转变为垂直于水平方向的位移g，可表示为：
[0229]
g(x)＝g(x)cosφ(x)
ꢀꢀꢀ
(37)
[0230]
式中：φ(x)为针轴轴线与水平方向夹角
[0231]
优选地，步骤2)中，在力学模型基础上，对针穿刺软组织过程中的单弯曲变形以及双弯曲变形的建模过程如下：
[0232]
对针穿刺软组织过程中的单弯曲的建模过程如下：
[0233]
系统能量π可以表示为：
[0234]
π＝u+w
ꢀꢀꢀ
(38)
[0235]
式中：u表示系统中的势能；w为外力对系统所做的功；
[0236]
柔性针与组织的相互作用过程构成一个受力系统，整个穿刺系统的能量可以分为：
[0237]
柔性针弹性势能
[0238]
柔性针刺入组织，组织被压缩，同时针体也会受到组织给予的反作用力，如夹紧力、切割反力、摩擦力等影响，针体会发生弯曲，此时便存在对应的弹性势能。对于一般弹性体而言，弯曲分为轴向弯曲和径向弯曲，在本研究中，由于柔性针轴向变形非常小，因此，只计算柔性针径向变形。柔性针的弯曲能ub可表示为：
[0239][0240]
式中：e为柔性针材料的杨氏模量；i为转动惯量；l
input
为针的长度；ρ为针的弯曲半径可以表示为：
[0241][0242]
组织压缩势能
[0243]
当柔性针刺入组织时，由于针排开组织占据了部分空间，导致组织被压缩，此时组织具有压缩势能us为：
[0244][0245]
式中：k
t
为组织弹簧刚度；y(x)为柔性针弯曲函数。
[0246]
轴向力及侧向力作功
[0247]
根据力学建模推导出轴向力f
x
及侧向力fy，进而得到做功表达式：
[0248][0249]
式中：l为针穿刺距离。
[0250]
针尾进给力作功
[0251]winput
＝f
p
l
input
ꢀꢀꢀ
(43)
[0252]
系统能量π可以表示为：
[0253]
π＝ub+us+w
input-w
m-wnꢀꢀꢀ
(44)
[0254]
利用瑞利-里兹法求取柔性针弯曲曲线，需要根据针的穿刺情况设定位移函数。在以往的研究中，柔性针通常被当做悬臂梁来进行研究，根据材料力学方面的知识，悬臂梁的位移函数通常为多项式，因此本文中的柔性针的弯曲位移情况也可以采用多项式表示。在保证准确性的基础上，为便于后期系数的求解采用三次多项式作为柔性针位移函数，表达式为：
[0255]
y(x)＝a+bx+cx2+dx3ꢀꢀꢀ
(45)
[0256]
穿刺过程和中的边界条件为：
[0257]
[0258]
最小势能驻值条件为：
[0259][0260]
通过分步求解得到系数a、b、c、d的值从而求得位移函数；
[0261]
对针穿刺软组织过程中的双弯曲的建模过程如下：
[0262]
柔性针在穿刺软组织过程中，斜尖方向的改变会导致穿刺方向发生变化，进而形成针的双弯曲轨迹。
[0263]
柔性针双弯曲穿刺过程分为三步：首先，柔性针穿刺形成单弯曲路径；其次，针尖转动180
°
；最后，柔性针继续穿刺，形成双弯曲路径。路径起点为原点o1，终点为o2(xb,yb)。为了便于分析，以单弯曲轨迹终点o2为原点，该点处切线为ξ轴建立新的坐标系ξo2η，ξ轴与水平线夹角为φ(xb)。在不考虑回弹的影响下，变换过程如下；
[0264]
坐标系变换：进行坐标系平移，使得两坐标系原点重合，再对坐标系旋转使得对应坐标轴重合，参考坐标系转换原则，两个坐标系中点的齐次变换矩阵为：
[0265][0266]
式中：(x,y)为单弯曲轨迹中的点；
[0267]
对称变换：将单弯曲曲线终点位置的切线确定为坐标变换的对称轴，并进行坐标变换。设切线方程为ax+by+c＝0，则对应变换后横、纵标为：
[0268][0269]
根据建立的单弯曲理论轨迹模型的曲线函数，结合上述坐标变换可得到无回弹下的双弯曲轨迹；
[0270]
在柔性针的第一段弯曲中的针尖旋转点为o2(xb,yb),则在不考虑回弹的前提下，新一轮的穿刺轨迹y(x)'可视为第一段穿刺轨迹y(x)绕点o2(xb,yb)旋转180
°
的结果，因此能得到如下关系:
[0271]
y(x)'＝2y
b-y(2x
b-x),(x＞xb)
ꢀꢀꢀ
(50)
[0272]
根据建立的单弯曲理论轨迹模型的曲线函数，结合上述坐标变换可得到无回弹下的双弯曲轨迹；
[0273]
联立公式(35)与公式(48)便可得到受回弹影响下的双弯曲曲线。
[0274]
以上显示和描述了本发明的基本原理和主要特征。本发明不受上述实施例的限制，上述实施例和说明书描述的只是发明的原理，在不脱离本发明的精神和范围的前提下，本发明还会有各种变化和改进，这些发明和改进都落入要求保护的本发明范围内。