一种基于量子计算的分子构象快速搜索方法与流程

1.本发明涉及分子构象搜索，尤其涉及一种基于量子计算的分子构象搜索方法。


背景技术：

2.在微观世界中，了解分子的结构和动力学对于了解其功能至关重要。分子构象途径描述了分子如何由于条件的变化而从一种构象转变为另一种构象，分子的构象空间复杂且高维，这使其分析成为一项极具挑战性的任务。
3.由于分子变化快速，通常很难通过实验表征中间结构和构象轨迹。在计算上，这也是一个具有挑战性的问题，因为基于物理学手段的模拟非常耗时，而且通常无法跨越足够的时间尺度来捕捉完整的路径。如最常见的配体和蛋白质结合问题，当配体分子与蛋白质通过诱导契合的方式结合时通常伴随着蛋白质的构象变化，这在计算上都是难以企及的。
4.为节省计算量，分子构象搜索常用作预测分子间结合构象的方法。分子构象搜索在生物学和药物研究中的研究和应用中很常见，包括药效团建模、过渡态搜索、蛋白质折叠和蛋白质从头设计等。例如，在研究蛋白质和配体对接时，搜索空间由蛋白质和配体的所有可能构象组成。以目前经典计算机的的计算资源，不可能穷尽这些搜索空间。有许多策略试图以最佳效率对搜索空间进行采样。
5.目前构象搜索的主流实现方式是：大多数分子对接模拟程序中分子构象搜索过程会将其中一个分子设置为刚性体，即便如此，构象搜索一个配体的所有构象异构体也是非常大的计算量，需要穷尽可旋转化学键和环以不同的角度旋转和翻转的组合。目前，这种基于刚性分子对接的虚拟筛选已成为药物发现的标准工具，用于识别靶向目标生物蛋白质分子的新型先导化合物。在该过程中，大多数对接程序将目标生物蛋白质分子视为刚性，只考虑配体分子的柔性。这种方式在其结果上取得一定程度的成功。
6.分子构象搜索涉及构象的全面采样和结构参数的组合。主要有随机搜索、全局搜索等方式。随机搜索是通过两种主要方法随机进行的：蒙特卡罗(mc)或遗传算法(ga)，都基于键旋转作为自由度形成不同的构象。主流软件的分子构象搜索方法包括：autodock4应用了遗传算法(ga)，autodockfr进一步提高了ga的有效性。autodock vina使用蒙特卡洛(mc)算法来提高运行时性能。galaxydock中还实施了构象空间退火(csa)作为全局优化方法。gwovina使用改进的灰狼优化器(gwo)替代autodock vina中使用的mc的全局搜索算法，以处理涉及更高柔性分子的对接问题。ledock使用进化算法和模拟退火搜索找到配体最佳构象。
7.这些构象搜索方式的局限性：由于目前的分子构象搜索方式为了降低搜索空间维度，通常人为设置其中一个分子为刚体结构，另一个分子作为配体是柔性结构，这种建模方式牺牲了精确度。即便如此，这类分子构象搜索空间也已经比较庞大，需要较大的计算资源展开搜索工作。如果将受体分子和配体分子都考虑为柔性，系统搜索可能会产生组合爆炸。
8.例如分子对接的重要应用领域创新药物开发，是一项耗资巨大且效率较低的工作，一般平均要筛选十万种以上的化合物才能得到一种新药。目前，已知的化合物分子数量
已达到数亿量级，使药物开发具备了大数据的基础，但同时也会要求提升化合物分子的构象搜索筛选过程的效率。
9.有效的搜索算法通常可以为对接软件提高准确估计配体结合亲和力或找到接近共结晶构象的概率，提高虚拟筛选的准确性和效率，量子计算比较适用于该类问题，并体现出其相对于经典计算的优越性。因此，基于量子计算进行分子构象搜索将有可能从根本上解决这些问题。


技术实现要素：

10.本发明旨在解决现有技术的缺陷，提供一种基于量子计算的分子构象快速搜索方法。本发明可以为对接软件提高准确估计配体结合亲和力或找到接近共结晶构象的概率，提高虚拟筛选的准确性和效率，并体现出其相对于经典计算的速度上的优越性。
11.本发明的技术方案是这样实现的，一种基于量子计算的分子构象快速搜索方法，在利用分子力场方法对原子间相互作用进行建模的基础上，运用量子编码方法，将能量或打分函数最小的分子构象搜索问题映射到量子计算机可以有效求解的伊辛耦合的自旋玻璃模型，采用哈密顿量量子算法求解该计算问题。
12.所述的一种基于量子计算的分子构象快速搜索方法，所述的量子编码方法是指把分子中相邻化学键之间的可能键角表示成一个二进制数的形式。
13.所述的一种基于量子计算的分子构象快速搜索方法，所述采用哈密顿量量子算法求解该计算问题中，需要的哈密顿量根据分子力场给出的相互作用、原子位置不可重叠、对称性等三个原则来定量得到。
14.所述的一种基于量子计算的分子构象快速搜索方法，采用哈密顿量量子算法求解该计算问题是一个哈密顿量基态问题，在量子计算机上通过量子振幅放大、量子绝热淬火、变分量子计算、qaoa、量子lanczos算法进行求解。
15.所述的一种基于量子计算的分子构象快速搜索方法，它包括将一个目标分子分解成n个基本的基团单元，分子的全局构象由相邻基团的化学键的旋转角度决定，因此构象搜索需要计算出n-1个旋转角度，每隔一定角度α进行构象采样，将每个化学键180
°
/α种不同的旋转角度编码致4个量子比特，结合量子比特信息对应的基团空间位置，基团之间的相互作用将表示为量子比特之间的耦合h
int
。量子计算中仍需考虑基团不能空间重叠、去除不合理旋转角度等约束条件，这些约束条件由量子哈密顿量中添加惩罚项实现分别为h
olap
、和h
constraint
；整体的哈密顿量表示如下：
16.h＝h
int
+h
olap
+h
constraint
；
17.在所构建的量子哈密顿量基础之上，采用相应的量子算法获得全局最优分子构象。
18.全局最优的分子构象搜索本质上是一个np-难的计算问题，其搜索空间大小与相应的计算复杂度随着构成分子的原子数目呈指数增长。经典计算为了降低计算复杂度，采用分子动力学模拟的方法，但是其结果不能保证全局最优。量子计算因为量子叠加原理具有天然的计算并行性，可以在整个分子构象空间进行整体性的并行运算，相比已有的经典算法可以获得指数级的量子加速，尤其对较大规模的分子构象搜索具有显著计算优越性。
19.本发明把分子构象搜索问题转换成了一个哈密顿量基态问题，在量子计算机上可
以通过量子振幅放大、量子绝热淬火、变分量子计算、qaoa、量子lanczos等算法进行求解。
20.本发明的搜索算法通常可以为对接软件提高准确估计配体结合亲和力或找到接近共结晶构象的概率，提高虚拟筛选的准确性和效率，量子计算比较适用于该类问题，并体现出其相对于经典计算的优越性。因此，特别是在提高效率方面，基于量子计算进行分子构象搜索将有可能从根本上解决这些问题。
附图说明
21.下面结合附图对本发明作进一步的说明：
22.图1是本发明的流程图。
23.图2和图3是实施例所述蛋白水解靶向嵌合体(protac)分子结构图与分子示意图。
具体实施方式
24.下面，结合实施例对本发明做进一步的说明，
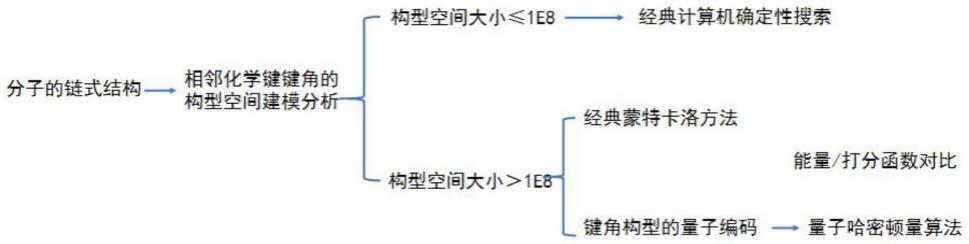
25.如图1所示，本发明所述的一种基于量子计算的分子构象快速搜索方法是根据分子的链式结构来确定相邻化学键键角的构型空间建模分析，构行空间大小以1eb为界，小于等于1eb的可采用经典计算机确定搜索；1eb以上的，采用量子计算，常规采用经典蒙特卡洛计算方法，本发明采用对分子键角构形的编码，将能量或打分函数最小的分子构象搜索问题映射到量子计算机，采用量子汉密尔顿算法对分子构形进行计算。
26.对分子键角构形的编码是将分子分解成m个基团单元，将相邻基团的化学键键角离散化成2n份，不同可能性由n个量子比特表示，运用基团间的相互作用定义所有(m-1)*n个量子比特之间的量子耦合，以此构建量子算法求解分子构象搜索需要的哈密顿量量子编码。如此，编码将把分子中相邻化学键之间的可能键角表示成一个二进制数的形式。进一步采用哈密顿量量子算法求解该计算问题。这一步需要的哈密顿量可以根据分子力场给出的相互作用、原子位置不可重叠、对称性等三个原则来定量得到。
27.实施例
28.选用蛋白水解靶向嵌合体protac为计算对象，其分子结构及分子示意图分别如图2、图3所示。
29.首先将分子分解成11个基本的基团单元。分子的全局构象由相邻基团的化学键的旋转角度决定，因此构象搜索需要计算出10个旋转角度。每隔5.625
°
(此参数可调节)进行构象采样，构型空间维度为32
10
约等于10
15
，随着链式分子中基团的数目的增长曾指数增长，经典计算难以精确处理。我们采用量子计算方法，将每个化学键32种不同的旋转角度编码致4个量子比特，则对于图2中的分子需要40个量子比特进行编码。结合量子比特信息对应的基团空间位置，基团之间的相互作用将表示为量子比特之间的耦合h
int
。量子计算中仍需考虑基团不能空间重叠、去除不合理旋转角度等约束条件，这些约束条件由量子哈密顿量中添加惩罚项实现分别为h
olap
、h
constraint
。整体的哈密顿量表示如下：
30.h＝h
int
+h
olap
+h
constraint
。
31.采用量子振幅放大、绝热量子退火、变分量子线路等量子算法进行量子哈密顿量基态运算，获得目标分子的全局最优构象。
32.在所构建的量子哈密顿量基础之上，采用相应的量子算法获得全局最优分子构
象。测试表明采用耦合强度为10ghz的量子退火机可以在1ms以内得到构象搜索结果。